控制器控制方式对永磁电机电磁场影响的研究
姜少义,李伟力,李 琳,李 栋
(北京交通大学,北京100044)
0 引 言
永磁电机系统具有逐步取代传统直流伺服系统的趋势,已成为现代伺服技术重要的发展方向[1]。永磁同步电机具有结构简单、效率高、功率因数高等多方面优势,符合高效节能的发展方向,在注塑机、数控机床、机器人、航空等行业已得到广泛应用[2-4]。
永磁同步电机需要控制器供电,而控制器供电时可能会增大定子输入电流的谐波含量,造成电机的定转子损耗增加,效率降低,并且影响电机工作时的温升,影响电机的使用寿命。因此研究控制器对永磁伺服电机的影响非常重要。
电机受控制器的影响,使其内部电磁场变的非常复杂。一般研究永磁伺服电机用理想电压源或者电流源作为电源,忽略了谐波的影响。为了更精确的计算控制器对电机内部电磁场的影响,本文采用了控制电路与电机瞬态有限元模型直接耦合的计算方法。研究了两种不同控制方式对电机电流、电压及其内部电磁场的影响。
1 电机与控制电路耦合模型
1.1 永磁同步电动机的结构
本文以一台永磁伺服同步电动机为研究对象,电机的主要参数如表1 所示,结构如图1 所示。

表1 电机的额定数据和主要尺寸

图1 永磁电机样机
1.2 永磁同步电动机数学模型的建立
由于电机采用细长型结构,电机内磁场沿轴向变化较小,本文采用二维模型对其电磁场进行计算。为了减小计算量,对电机的电磁场模型进行如下假设[5-9]:
1)忽略位移电流的影响;
2)忽略电机端部漏磁,采用二维电磁场分析时,磁位只有z 轴分量Az;
3)不计材料磁导率随温度的变化。
在以上假设的基础上,根据永磁伺服电机的实际结构,建立了如下的数学模型:

式中:Az为磁矢位;Jz为传导电流密度;μ 为磁导率;σ 为电导率;Js为永磁体等效电流密度;t 为时间。
1.3 方波与正弦波控制电路搭建
基于Simplorer 分别搭永磁同步电机方波与正弦波控制系统。控制器系统模型中开关管选用IGBT,续流二极管选取二极管模块Diode。场路耦合控制电路主电路如图2 所示。

图2 逆变器主电路图
1.3.1 方波控制电路搭建
方波控制采用三相六状态控制运行。任意时刻两相绕组通电,每60°换相一次,每相绕组连续通电120°[10]。方波控制场路耦合系统如图3 所示。

图3 方波控制场路耦合系统图
1.3.2 正弦波控制电路搭建
正弦波控制采用基于电压空间矢量脉宽调制的控制方式[11]。SVPWM 由三相桥式逆变器的6 个功率开关元件组成的特定开关模式产生的脉宽调制波,能够使输出电流波形尽可能接近于理想的正弦波形。采用电流转速双闭环策略。正弦波控制系统如图4 所示。
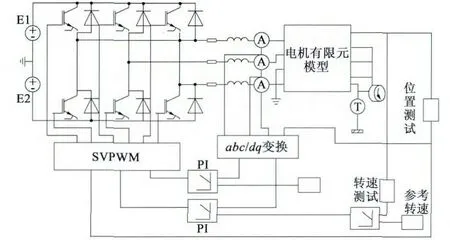
图4 正弦波控制场路耦合系统图
2 方波、正弦波控制方式对电机的影响
2.1 方波、正弦波控制对电机电压、电枢电流的影响分析
永磁电机的控制方式不同,导致三相逆变桥中6 个IGBT 开通关断及导通时间不同,影响到加载在电机上的驱动电压及其电流,使电枢电流含有的谐波幅值不一样[12]。本文利用控制电路与电机瞬态有限元模型直接耦合这个优势,研究了控制方式对电机的影响。方波控制与正弦波控制输入电机的电压波形如图5 所示。

图5 两种控制方式电机相电压谐波分析
由图5 可以看出,方波控制时电机相电压2 到10 次谐波含量比正弦波控制时相电压谐波含量高很多。例如方波控制时电机相电压的3 次谐波幅值为80 V,而正弦波控制时电机相电压3 次谐波幅值为15 V。方波控制电机相电压谐波分布规律与正弦波控制相电压谐波分布规律不同;且电压高次谐波,比如39 次、79 次、137 次等电压谐波,方波控制比正弦波控制小。
由图6 可以看出,正弦波控制时电机电枢电流更接近理想正弦波,而且其波形比较平滑。造成这种现象的原因是方波控制时电枢电流谐波含量比正弦波控制时大很多引起的。方波波控制时电枢电流有效值为28.9 A,正弦波控制时电枢电流有效值为25.5 A。方波控制时电机电枢电流比正弦波控制时大了3.4 A,其主要原因是由于方波控制时电流谐波含量比正弦波控制时电流谐波含量大很多引起。
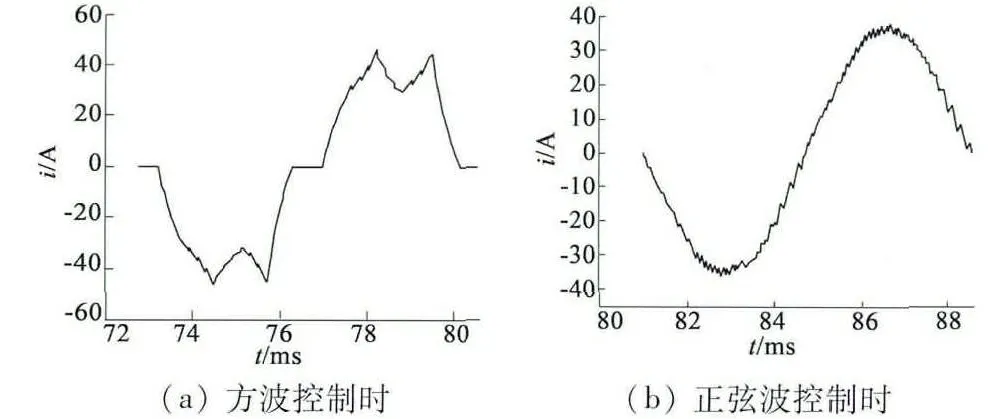
图6 两种控制方式电机电枢电流波形图
2.2 方波、正弦波控制时电机磁密分析
从前面分析可知,控制方式不同,电压、电流谐波含量不同,进而影响到电机内部电磁场。本文详细研究了两种控制方式对电机内部电磁场的影响。
图7 为方波与正弦波控制时电机稳态运行各部分磁密分布云图。从图7 可以看出,对于本样机,两种控制方式电机磁密最大值都出现在电机定子齿部。方波控制时电机整体磁密比正弦波控制时大。方波控制时电机磁密最大值为2.07 T,正弦波控制时电机内部磁密最大值为2.02 T,比方波控制时电机最大磁密小了0.05 T。
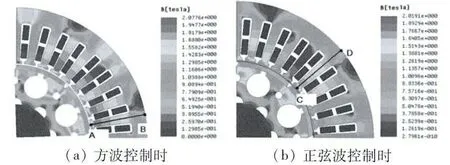
图7 两种控制电机稳态运行磁密分布云图
为了研究电机稳态运行定子齿部磁密情况,在图7(a)和图7(b)中分别选取了方波控制与正弦波控制定子齿部磁密最大的齿部中心线AB 和CD 为研究对象,方波控制时齿部中心线AB 的磁密分布和正弦波控制时齿部中心线CD 的磁密分布,如图8(a)和图8(b)所示。
从图8(a)方波控制最大磁密的齿部中心线AB可以看出,从齿顶A 点到轭背部B 点径向磁密(图8(a)中曲线1)变化规律是由低到高,然后又由高到低,其中最大磁密出现在齿肩处,最小磁密出现在轭背部区域。从图8(b)正弦波控制最大磁密的齿部中心线CD 可以看出,从齿顶C 点到轭背部D 点径向磁密(图8(b)中曲线3)变化规律是由低到高,然后又由高到低,其中最大磁密出现在齿肩处,最小磁密出现在轭背部区域。类似的,从图8(a)方波控制最大磁密的齿部中心线AB 可以看出,从齿顶A 点到轭背部B 点切向磁密(图(a)中曲线2)变化规律是由高到低,然后又近似于一条直线,其中最大磁密出现在齿顶区域,最小切向磁密出现在齿肩。图8(b)正弦波控制最大磁密的齿部中心线CD 可以看出,从齿顶C 点到轭背部D 点切向磁密(图(b)中曲线4)变化规律是也是由高到低,然后又近似于一条直线,其中最大磁密出现在齿顶区域,最小切向磁密出现在齿肩。

图8 电机齿部与轭部磁密分量曲线图
由图8 可以看出,对于本样机,方波控制时电机定子轭部径向磁密比正弦波控制时稍大。而方波控制时定子齿磁密径向分量最大值为1.91 T,正弦波控制时为1.79 T,正弦波控制时比方波控制时小了0.12 T。而且,方波控制时电机定子齿部最大磁密比正弦波控制时定子齿部最大磁密大,因此造成方波控制时定子铁耗大:方波控制电机定子铁耗为150.6 W,而正弦波控制时电机定子铁耗为126.6 W。且电机工作在重载工况时,若采用方波控制方式则电机定子齿更容易饱和。
对于本样机,方波控制时电机相电流比正弦波控制时相电流大了3.4 A。因此,方波控制时电机电枢反应更强烈,造成气隙磁密基波幅值比正弦波控制时的气隙磁密基波幅值稍大,如图9 所示。且方波控制时电机气隙磁密谐波含量总体上比正弦波控制时气隙磁密谐波含量大,造成方波控制时电机护套涡流损耗比正弦波控制时护套涡流损耗大了9.8 W。

图9 两种控制方式时电机气隙磁密谐波分析图
3 方波、正弦波控制方式下转矩波动研究
对于方波控制,电机电磁转矩与电枢电流成正比关系。当电流恒定时,电磁转矩恒定不变。然而,由于定子绕组电感的存在,当电机换相时电流波形不能突变,即关断相的电流不会立即变为零,导通相电流也不可能立即变为稳态值,每次换相时电枢电流都会出现一个缺口,如图6(a)所示,因此转矩也不能保持恒定,从而产生转矩波动。而正弦波控制时电枢电流波形较为平滑,谐波含量少,从而使转矩波动比方波控制时小很多。图10 为方波控制与正弦波控制时电机电磁转矩波形图。

图10 方波与正弦波控制时电机转矩
由图10 可以看出,对于此样机,方波控制时转矩波动比正弦波控制时转矩波动大很多:方波控制时电机转矩波动为45 N·m,而正弦波控制时电机转矩波动为8 N·m。
4 样机测试
样机在额定负载情况下进行了测试。如图11所示。图11 中左下方为控制器,左上方为样机,右侧为直流电机负载。样机由正弦波控制器供电,以直流发电机作为负载,通过改变直流机励磁电流的大小控制负载大小,最终确定样机运行在额定负载、额定转速情况。

图11 样机测试系统
正弦波控制器试验测得电机额定负载额定转速测试结果如表2 所示。通过对不同控制方式下场路耦合模型计算得到与实测工况相同,即额定转速、额定负载时电机的相电压与电枢电流计算结果。
从表2 可以看出,正弦波控制计算结果与实测结果相比,电流相对误差为5. 3%,线电压误差为0.054%。而方波控制电机相电流比正弦波控制时大,这是由于方波控制时电流谐波大引起,前面已经分析。

表2 样机实测结果及计算结果
由于实验条件限制,本文只对正弦波控制进行了实验测试,从计算结果与测试结果来看,计算误差较小,说明计算方法是准确的。
5 结 语
本文采用控制电路与电机瞬态有限元模型直接耦合的计算方式,研究了方波、正弦波两种控制方式对永磁电机电压、电流、电机内部磁密分布及其损耗的影响。可以得出如下结论:
永磁电机运行在额定状态,方波控制时电枢电流谐波含量比正弦波控制时大很多,造成方波控制时电枢电流比正弦波控制时大了3.4 A。方波控制时电机定子齿最大磁密比正弦波控制时定子齿磁密最大值大了0.058 T,且方波控制时磁密最大的齿部中心线上径向磁密最大值比正弦波控制时大了0.12 T;造成电机方波控制时定子铁耗比正弦波控制时大,并且可以推测电机工作在重载情况时定子齿更容易饱和。方波控制时电机气隙磁密谐波含量比正弦波控制时电机气隙磁密谐波含量大,造成方波控制时转子护套涡流损耗比正弦波控制时转子护套涡流损耗大。对于此样机,方波控制电机电磁转矩波动比正弦波控制时电机电磁转矩波动大了5.6 倍。
[1] 陶果,邱阿瑞,柴建云,等.永磁同步伺服电动机的磁场分析与参数计算[J].清华大学学报,2004,44(10):1317 -1320.
[2] 唐任远.现代永磁电机理论与设计[M]. 北京:机械工业出版社,2011:3 -4.
[3] 王秀和.永磁电机[M].北京:中国电力出版社,2010:7 -8.
[4] 刘景辉.注塑机用永磁同步电动机的研究与设计[D]. 广州:广东工业大学,2012.
[5] 张晓晨,李伟力,邱洪波,等.超高速永磁同步发电机的多复合结构电磁场及温度场计算[J]. 中国电机工程学报,2011,31(30):85 -92.
[6] LANCAROTTE M S,PENTEADO A D,PAULOS A J.Prediction of magnetic losses under sinusoidal or non - sinusoidal induction by analysis of magnetization rate[J]. IEEE Transactions on Energy Conversion,2001,16(2):174 -179.
[7] 冯慈章.电磁场[M].北京:人民教育出版社,1979:96 -117.
[8] 唐丽.微型燃气轮机驱动的高速永磁发电机电磁场及温度场计算[D].哈尔滨:哈尔滨理工大学,2009.
[9] 汤蕴璆.电机内电磁场[M].2 版.北京:科学出版社,1998:122-154.
[10] 白利飞,马瑞卿,张庆超. 无刷直流电动机PWM 斩波方式分析[J].微特电机,2013,41(2):21 -24.
[11] 李莹.基于变频器供电的潜油电机的性能分析[D]. 哈尔滨:哈尔滨理大学,2008.
[12] 韩静静.PWM 逆变器供电对异步电动机铁芯损耗影响的研究[D].北京:北京交通大学,2011.

