基于负载观测器的步进电动机滑模位置控制
董 雷,杨向宇,赵世伟
(华南理工大学,广州510642)
0 引 言
步进电动机是一种将电脉冲信号转换成相应角位移或线位移的控制电机,具有误差不积累、结构简单、体积小、价格低廉、控制方便等优点,因而被广泛应用在数控、印刷、喷绘、光学定位、机器人等行业[1]。传统的步进电动机驱动器多采用开环运行方式,其成本低,控制简单,但抗扰动性差,易失步,因此,目前对步进电动机控制的研究主要集中在闭环上。
步进电动机最常见的闭环控制策略是传统PID控制,其参数整定较为繁琐,且对运行工况的适应能力较差,在系统快速性和稳定性上也难以同时兼顾。文献[2]根据步进电动机的线性或近似线性模型,推导了全局稳定的自适应控制算法,实现了给定信号较好的跟踪,但该控制算法严重依赖于电机模型参数。文献[3 -4]研究了模糊逻辑控制算法在步进电动机闭环控制系统中的应用,但所用模糊控制规则过分依赖于经验和专家知识。文献[5]将遗传算法、神经网络和PID 控制相结合,设计基于遗传算法优化的RBF 神经网络PID 控制器并应用到步进电动机位置控制系统中,得到了较高精度的定位效果,但该算法复杂,实现较为困难。文献[6 -7]研究了滑模控制算法在永磁同步电机速度控制中的应用,提高了系统的动态性能和抗扰动能力。滑模控制器参数少,设计简单,响应速度快,对系统参数的摄动及外部扰动具有较强的鲁棒性。
本文对两相混合式步进电动机的位置控制系统进行了滑模算法设计,针对负载扰动设计了负载观测器,在此基础上进行了Simulink 仿真和相应的实验,并将滑模控制算法与传统PID 控制的控制效果做了对比分析。
1 两相混合式步进电动机的结构和数学模型
1.1 两相混合式步进电动机的结构
本文采用的混合式步进电动机定子为两相八极,转子50 个齿,如图1 所示。定子上均匀地分布着8 个磁极,每个磁极的极靴上又均匀地分布着5个小齿,定子磁极上的小齿齿距与转子的小齿齿距相同。转子由环形磁钢和两段铁心组成,环形磁钢在转子中部,在安装时两段转子铁心错开半个齿距。
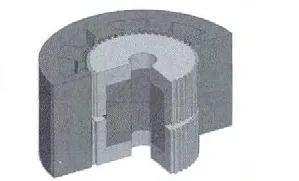
图1 两相混合式步进电动机三维结构图
1.2 两相混合式步进电动机的数学模型
采用简化的磁网络模型,经化简整理可得系统的电压方程和转矩方程:
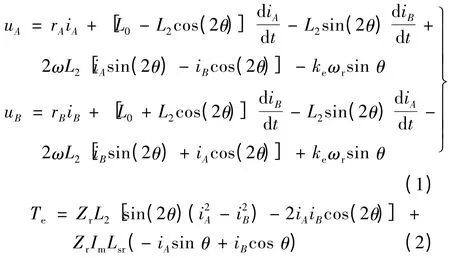
运动方程:
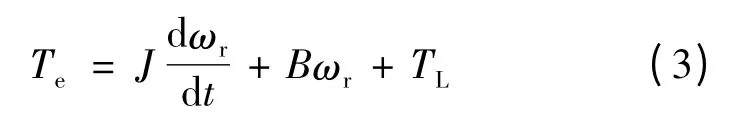
式中:ui,ii,ri(i=A,B)分别为定子相电压、相电流、相电阻;θ,ωr,ω,Zr分别为转子位置电角度、转子机械角速度、转子电角速度和转子齿数;L0,L2分别为电感基波和二次谐波恒定分量;J,B,TL分别为转动惯量、粘滞摩擦系数和负载转矩;Im,Lsr分别为永磁体等效成的转子电流和定转子互感的恒定分量;ke为反电势系数,其大小等于ZrLsrIm。
经坐标变换得d-q 旋转坐标系下的转矩方程:
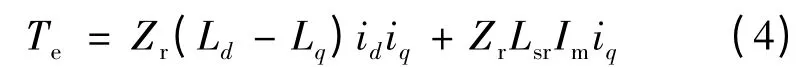
在磁场定向的矢量控制中,为便于控制,一般采用id=0 的控制方式,因此,式(4)简化:

式(3)和式(5)联立可得:
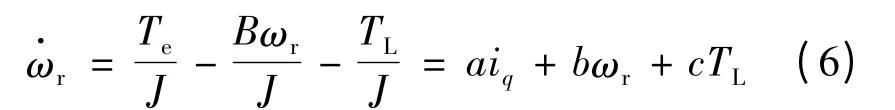
2 滑模控制器的设计
2.1 滑模面的选择
为了在算法上较易实现和满足步进电动机位置控制的性能要求,本文选用常见的线性滑模面,其表达式:

式中:C 为状态矩阵,X 为状态向量。
设θ*为步进电动机给定位置,θ 为转子实际位置。令e = θ*- θ,x1= e,x2=,u = iq。联立式(6),可得步进电动机的位置误差状态方程:
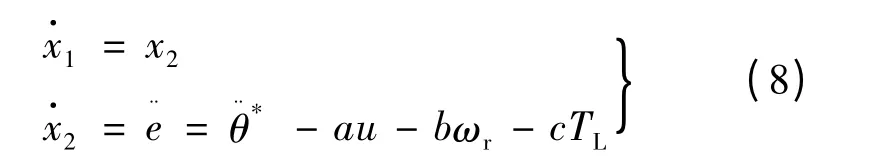
因此选择滑模面:

2.2 趋近律的改进
选择合适的滑模趋近律并加以改进可以使系统得到较好的性能,并且能够有效削弱抖振。常规指数趋近律的不足之处在于其切换带为带状,系统在切换带中向平衡点运动时,最后不能趋近于平衡点,而是在趋近于平衡点附近进行抖振,这可能激发系统未建模的高频成分。文献[8]给出了一种变指数趋近律:
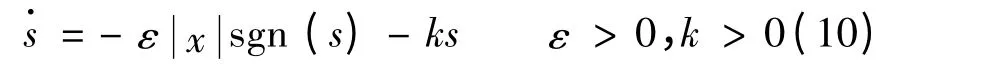
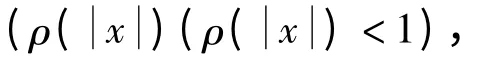
修正后的时变切换增益ε':

采用饱和函数sat(s)代替理想符号函数sgn(s)能够进一步削弱系统抖振:
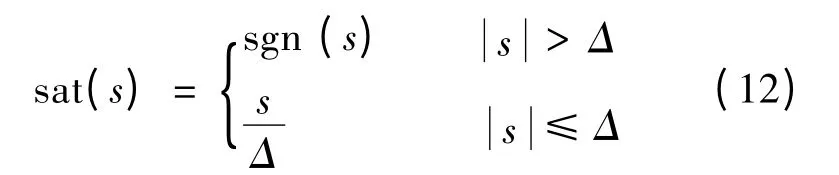
Δ 为一个数值较小的正常数。
因此,本文最终采用的趋近律表达式如下:
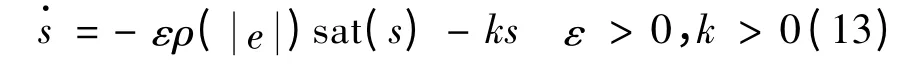
联立式(8)、式(9)、式(13),可得控制率:
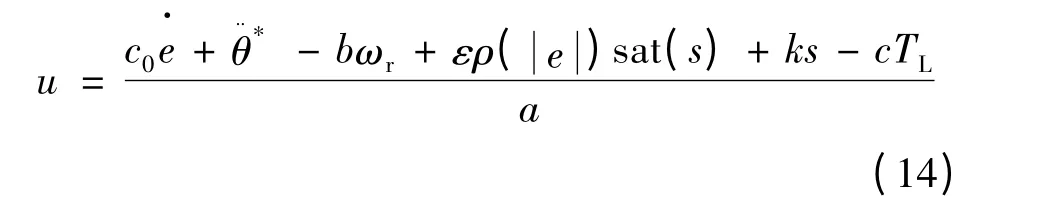
2.3 稳定性分析
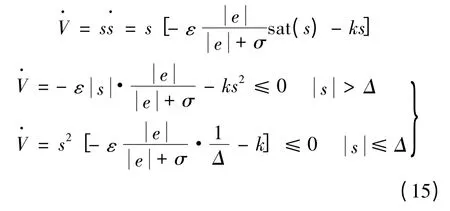
3 负载转矩观测器的构建
传统的负载转矩降阶观测器只利用积分进行辨识[9-10],辨识收敛速度较慢。本文将比例和积分同时加入到负载转矩的辨识中,可提高负载转矩辨识的收敛速度。
由于控制器采样时间远远小于扰动转矩的变化时间,所以视负载扰动转矩为一个状态变量,且假定它是一个恒值,则有=0。结合式(6),得系统状态方程如下:
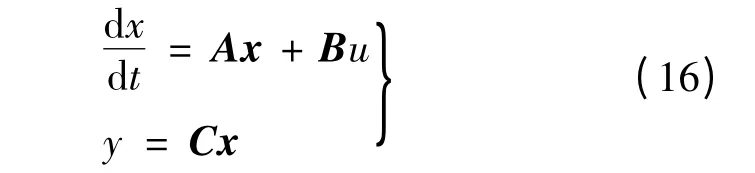
构建负载转矩观测器:
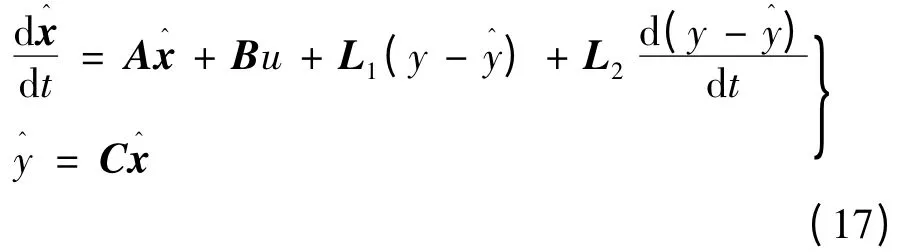
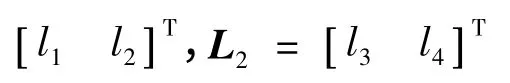
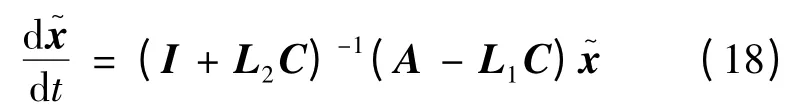
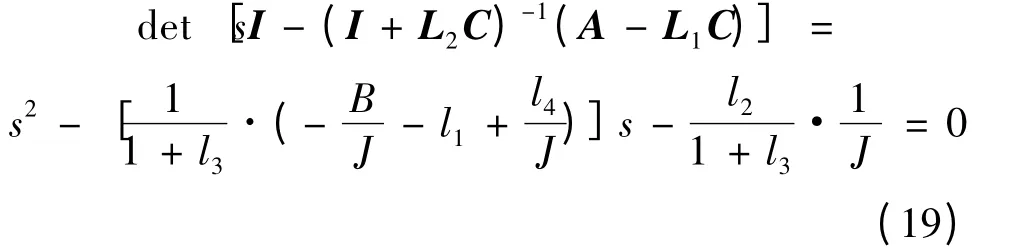
设系统特征根为s1,s2,并假定B =0,设计l1=l3=0,则状态反馈系数l2,l4的值:
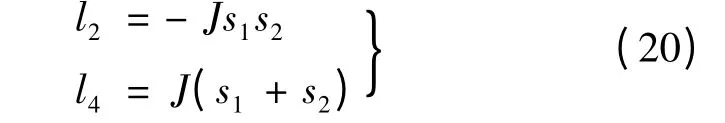
由式(19)可得观测器的极点:
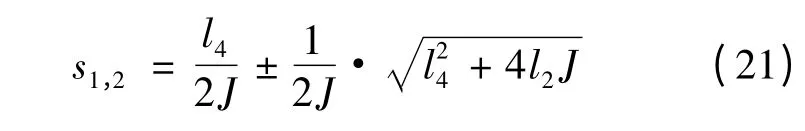
根据李雅普诺夫第一法,为使系统稳定,需满足Re[s1]<0,Re[s2]<0,设观测器的两个极点都配置在s1=s2= -sp处(sp>0),因此可得l2= -,l4=-2Jsp。根据系统期望的特性选择极点所在的位置,按照式(17)构建负载观测器,即可观测出TL的值。
为实现状态观测器的数字化控制,将式(17)进行离散化,即可得到转速和负载转矩观测值的递推公式:
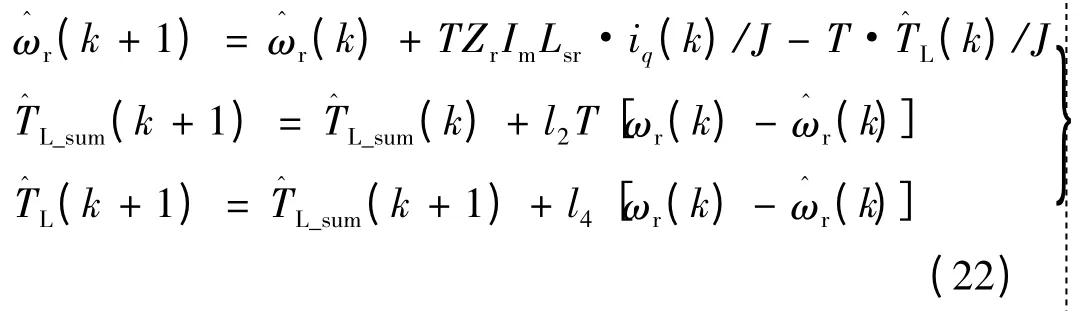
4 控制系统仿真结果及分析
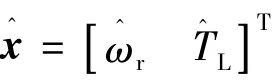
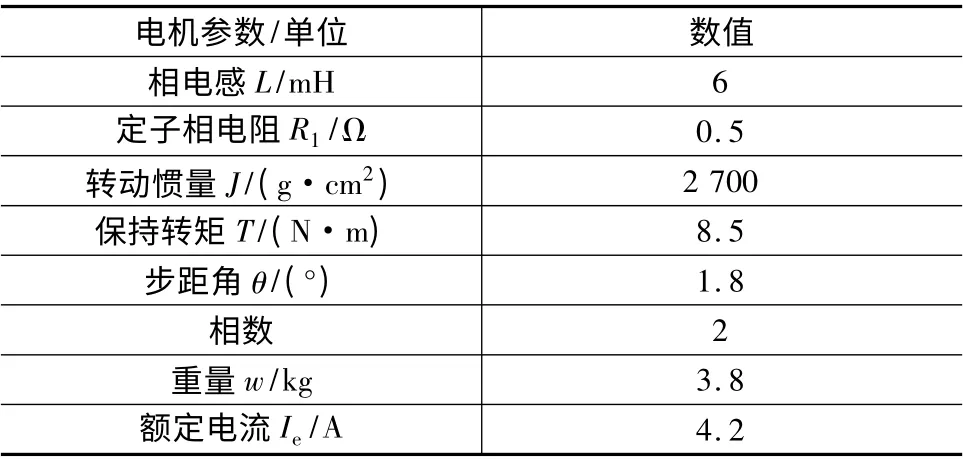
表1 两相混合式步进电动机的参数
系统分别跟踪方波和锯齿波指令信号,方波指令为周期3 s,幅值45°的位置信号,步进电动机首先空载运行,在1.5 s 时突加2 N·m 负载转矩;锯齿波指令为周期1 s,幅值180°的位置信号。仿真过程中采用相同的PID 控制器和滑模控制器参数,其位置响应曲线如图2、图3 所示。
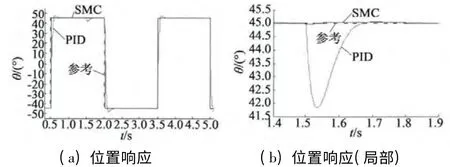
图2 跟踪方波指令仿真波形
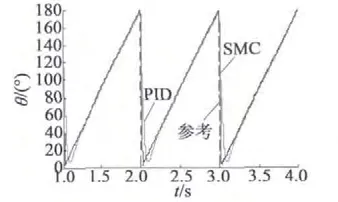
图3 跟踪锯齿波指令仿真波形
从图2 (a)可以看出,步进电动机在空载运行时,与传统PID 控制相比,采用滑模控制器能更快地跟踪方波位置信号且基本上没有超调;突加负载时,电机在PID 控制方式下有一个较为明显的位置跌落和回升过程,而在滑模控制方式下位置跌落较小,回升较快,如图2 (b)所示。
图3 显示,使用相同的控制器参数跟踪锯齿波位置信号时,滑模控制的响应速度更快,位置误差更小。由此可以看出,在两相混合式步进电动机的位置控制系统中,滑模控制可以得到比传统PID 控制更好的动态性能,而且对不同性质指令和负载扰动具有更强的鲁棒性。
5 实验结果及分析
本文采用的实验平台如图4 所示。系统由一台86 式两相混合式步进电动机、驱动板、直流电源和上位机组成,电机相关参数同表1。为了便于对比仿真结果,在该实验平台下,系统使用两种控制器分别跟踪上述两种位置指令信号。实验结束后,将上位机两个采样通道中相同时间段内的数据取出,并用MATLAB 重新绘制,实验波形如图5、图6 所示。

图4 实验平台
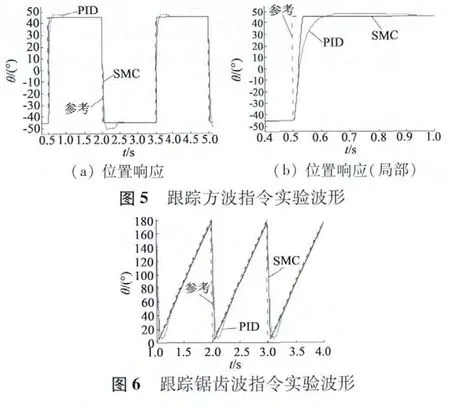
对比实验波形与仿真波形可以看出,两者结果基本一致。两种控制器都可以使步进电动机快速准确地跟踪方波指令信号,且基本上无稳态误差,但滑模控制的动态响应时间略短于PID 控制且基本无超调,如图5(b)所示。另外,由于实际步进电动机正反转的模型参数和特性不完全对称,PID 控制在跟踪方波指令信号时正负超调稍有差别,如图5(a)所示。图6 显示,使用相同的控制器参数跟踪锯齿波指令信号时,滑模控制的控制效果更好。以上实验结果验证了滑模控制在实现两相混合式步进电动机位置控制上的可行性和优越性。
6 结 语
本文针对两相混合式步进电动机的位置控制系统,采用改进的具有时变切换增益的指数趋近律对其进行了滑模算法设计,并针对负载扰动构建了负载观测器,在Simulink 环境下搭建了仿真模型,并进行了相应的实验验证。仿真和实验结果表明该算法相比于传统PID 控制,在位置跟踪上具有更好的动态性能,使系统具有更强的鲁棒性。
[1] 苏义鑫,孙功武,聂巍. 基于矢量控制的步进电动机细分驱动技术[J].微特电机,2014,42(2):56 -59.
[2] MARINO R,PERESADA S,TOMEI P. Nonlinear adaptive control of permanent magnet step motors[J]. Automatica,1995,31(11):1595 -1604.
[3] 刘川,刘景林.基于Simulink 仿真的步进电机闭环控制系统分析[J].测控技术,2009,28 (1):44 -49.
[4] 高向东,黄石生,余英林.步进电机模糊控制技术的研究[J].微特电机,1999,27(3):3 -5.
[5] 金路,罗晓曙,姜东东.单细胞分析仪中步进电机的定位控制[J].自动化与仪表,2014,(12):38 -42.
[6] 汪海波,周波,方斯琛. 永磁同步电机调速系统的滑模控制[J].电工技术学报,2009,24(9):71 -77.
[7] WANG Ai-meng,JIA Xing-wang,DONG Shu-hui. A new exponential reaching law of sliding mode control to performance of permanent magnet synchronous motor[J].IEEE Trans on Magnetics,2013,49(5):2409 -2412.
[8] 欧阳叙稳,尹华杰,叶长青. 永磁同步电动机滑模控制仿真[J].微特电机,2011,39(8):38 -40,50.
[9] 山炳强,于海生.基于负载观测器的永磁同步电机反步法控制[J].电机与控制应用,2006,33(7):33 -36.
[10] 鲁文其,胡育文,梁骄燕,等. 永磁同步电机伺服系统抗扰动自适应控制[J].中国电机工程学报,2011,31(3):75 -81.

