直驱式全功率变流器机侧无传感器控制策略研究

顾 凯，魏海峰，张 懿

(江苏科技大学，镇江212003)

0 引 言

直驱风力发电系统成为当前风力发电系统的重要发展方向，目前，国内外学者已加大对直驱式风电变流器控制技术的研究。直驱式风电变流器机侧主要对永磁同步电机进行控制。永磁同步发电机(以下简称PMSG)与传统发电机相比，具有结构简单、效率高等优点，转速可以设计得较低，并且易于实现并网、兼具有功和无功可控、低谐波等优势［1］。目前工程中常用的控制方式有矢量控制和直接转矩控制，矢量控制采用电流闭环控制，可以实现对发电机连续且平滑的控制，并且调速范围较宽;而直接转矩控制，存在转矩脉动，影响低速性能，同时调速范围受到了限制，无论采用哪一种控制，都需要知道发电机转子精确的位置。但是，风力发电机的应用环境通常比较恶劣，采用传统安装光电编码器或旋转变压器等装置进行检测，容易受到干扰，传感器易损坏，这样不仅增加设备成本，而且安装和维修都比较困难，影响了系统的稳定性，因此永磁同步电机无传感器控制技术，对于直驱式全功率变流器的发展具有重要意义［2］。关于无传感器控制技术，国内外已有大量的研究。目前，实现永磁同步电机无传感器控制主要通过利用定子端电压和电流直接估算、基于状态观测器估计和凸极跟踪等方法［3］。

本文研究了一种机侧变流器采用id=0 的转速外环、电流内环的双闭环控制策略。该控制策略控制系统简单，不会引起去磁反应和永磁同步电机退磁现象，实现定子电流与转子磁通解耦控制，良好的转矩特性，可以获得很宽的调速范围，比较适合永磁同步电机。无传感器采用一种数字锁相环和模型参考的方法，并在公司2 MW 直驱式全功率变流器样机上进行了验证，实现了预期的控制效果。

1 PMSG 数学模型

要设计PMSG 控制策略，需要对其进行理论分析，而目前常用的理论分析方法是通过建立电机数学模型进行研究。对于电机有三种不同坐标系下的数学模型，每个数学模型适用于不同的理论分析，本文根据研究需要，建立PMSM dq 轴下的数学模型［3-4］。电机参数矢量图如图1 所示。

在这些假设下，以电动机惯例为电流的参考方向，最后得到永磁同步电机在同步旋转坐标系d，q轴下的数学模型:

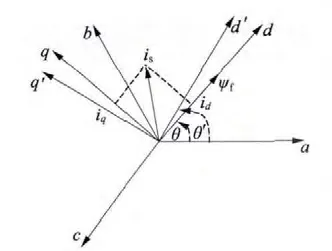
图1 d，q 坐标系矢量图

电压方程:

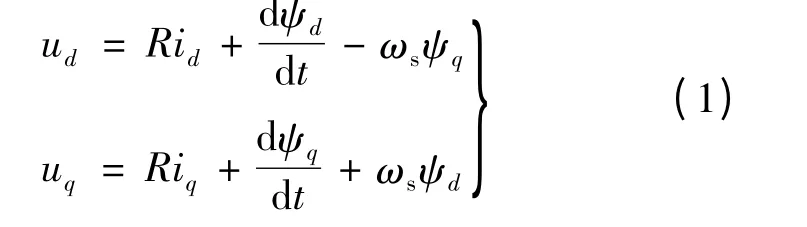
式中:ud，uq分别是d 轴和q 轴的定子电压分量;ωs是转子电角速度;R 是定子电阻。

磁链方程:

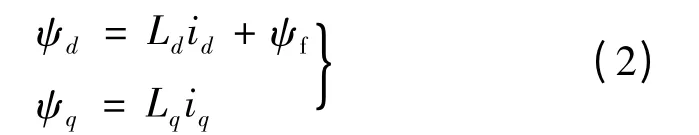
式中:ψd，ψq分别是d，q 轴的磁通;Ld，Lq分别是d轴和q 轴的电感;ψf为转子磁链。

电磁转矩方程:

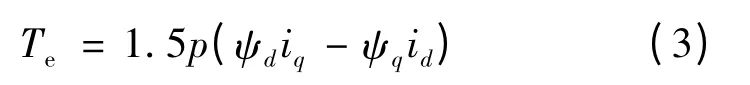
式中:p 为电机极对数;Te为电磁转矩。

机械运动方程:

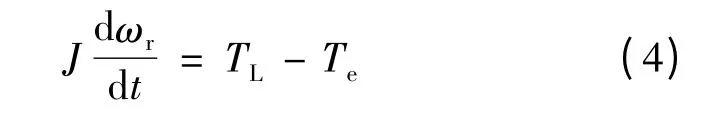
式中:ωr是发电机转子的机械转速;TL为原动机转矩。

2 机侧变流器控制策略

2.1 id =0 矢量控制策略

机侧变流器的控制策略示意图如图2 所示。本文采用转速、电流双闭环矢量控制策略，通过调节发电机定子电流dq 轴分量，实现对发电机的电磁转矩和定子无功功率的控制［5-6］。采取id=0 控制方式，将定子电流全部用于产生电磁转矩，从而实现发电机最大转矩、最小损耗、最大效率的控制［7-8］。外环控制中，风力机实时风速和发电机实际转速计算得到转速度参考值ω*，再将转速实际值与转速参考值的差值，通过PI 调节器进行调节得到q 轴电流参考值。将id=0 代入式(3)中，可得到电磁转矩和iq的线性关系，所以发电机的电磁转矩只存在唯一的变量，即q 轴电流iq。因此，只需要对定子电流在q 轴上的电流分量iq进行调节就可以实现对发电机电磁转矩的控制功能，同时使转速实际值跟随转速参考值ω*。采用Clarke 和Park 变换，将电机三相静止坐标系下的定子电流ia，ib和ic进行变换，得到两相旋转dq 坐标系下的电流值id和iq。机侧为了实现独立控制dq 轴电流和消除电网电压扰动，引入电压前馈补偿控制，同时引入两轴的反馈电流ωLdid和ωLqiq解耦项，使有功电流和无功电流可以分别独立控制。最后得到了要调制的电压ud和uq，再将ud和uq进行反坐标变换后送入SVPWM 脉宽调制产生驱动信号。

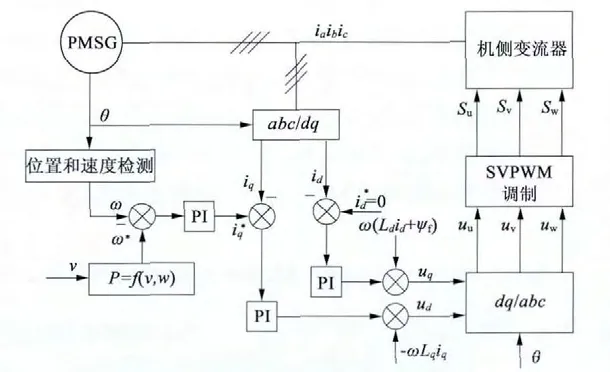
图2 机侧变流器控制策略示意图

2.2 无速度传感器控制策略

本文采用的数字锁相环实现了永磁同步电机的无速度传感器控制技术。图1 中dq 轴是实际转子位置坐标系，d'q'轴为估计转子位子坐标系。由前面分析可知，PMSG 电磁转矩仅与iq成正比而与id无关。当id=0 时，单位电流产生的转矩最大，即电流利用率最高，所以在保证dq 坐标系d 轴与d'重合前提下控制d 轴电流为零［9］。为此本文采用了一种旋转坐标系闭环控制策略，该策略根据d 轴与d'轴线的角度差来调整同步旋转坐标系的旋转速度，进而保证d 轴与d'轴重合。当d 轴与d'轴线重合时，Δθ=θ' -θ=0。为了计算需要，将电压方程改写成:

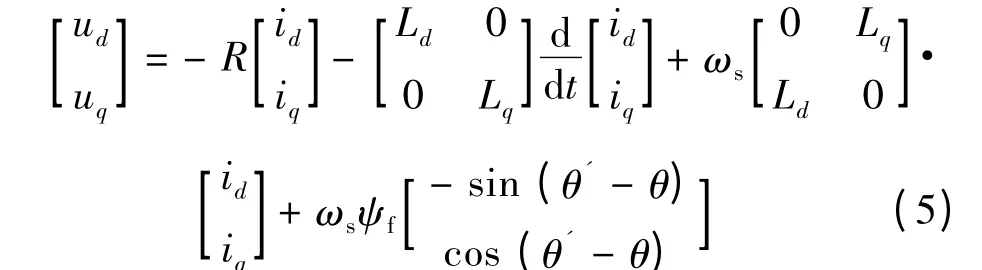
由式(5)可以推出:

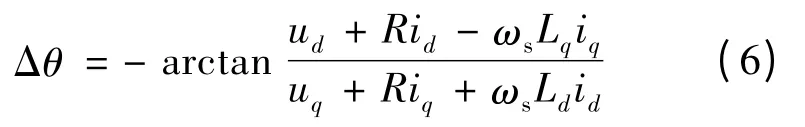
式(6)中，忽略了不容易获得的电流微分信号部分，而且电流微分信号容易引入干扰，并且稳态时基本为零。根据分析及式(5)和式(6)，可知，通过PI 调节器控制Δθ =0 就可实现锁相功能。图3 是锁相环的控制原理图，将PMSG 输出的电压和电流经过坐标变换得到dq 轴分量，经过锁相环算法得到Δθ，再经过PI 调节器调节Δθ=0，得到转子角速度，经过积分环节后就可得到转子位置角。

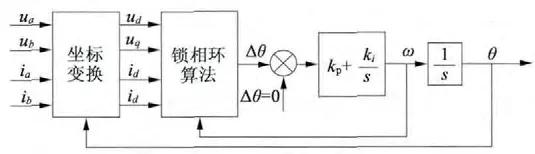
图3 三相数字锁相环控制原理图

3 实验结果与分析

为了检测理论的正确性和可行性，在某公司2 MW 直驱式全功率变流器样机上进行了实验验证。图4 和图5 分别为机侧三相电流波形和直流侧电压波形，从波形上可以看出，机侧三相电流波形接近于正弦波，且波形比较平滑，相序和幅值均达到了设计要求。直流侧电压也稳定在1 000 V 左右。实验结果表明了本文研究的控制策略在工程应用中的可行性。测试平台相关参数如表1 所示，测试波形显示皆为标幺值。

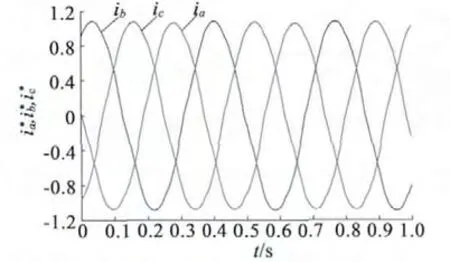
图4 机侧三相电流波形

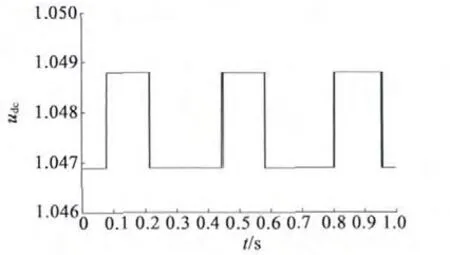
图5 直流侧电压波形

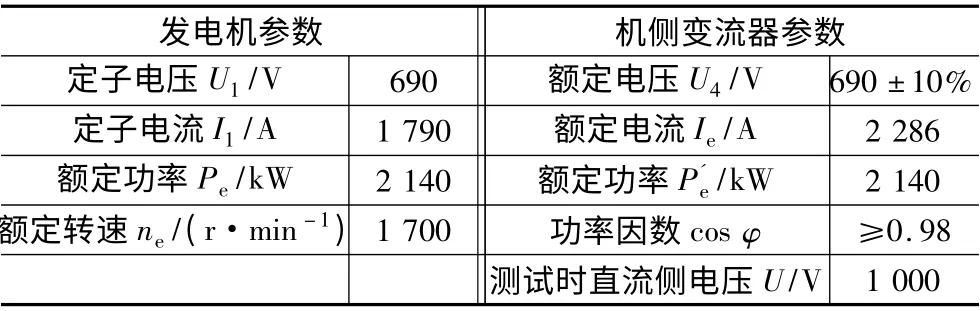
表1 测试平台相关参数

4 结 语

根据实际应用的需要，本文研究一种基于数字锁相环的无速度传感器矢量控制技术，该控制策略简单易行，便于工程实现。经过理论分析和样机实验，测试结果表明该控制策略能够准确算出风力发电机转子的位置，在直驱式全功率变流器上体现了良好的控制性能。

［1］ 范长宝，张洪阳，朱建光，等.永磁直驱全功率变流器控制策略［C］//第十届全国永磁电机学术交流会论文集.2010:119 -124.

［2］ 付明星，李明成，马培锋，等.永磁直驱风电变流器无传感器控制研究［J］.电气传动，2014，44(2):11 -14.

［3］ 唐芬，金新民，姜久春，等.兆瓦级直驱型永磁风力发电机无位置传感器控制［J］.电工技术学报，2011，26(4):19 -25.

［4］ 汪海波，周波，方斯琛. 永磁同步电机调速系统的滑膜控制［J］.电工技术学报，2009，24(9):72 -75.

［5］ 胡书举，许洪华.直驱风电系统PMSG 有无速度传感器控制比较［J］.高电压技术，2009，35(12):3129 -3131.

［6］ 胡书举，王剑飞，赵栋利，等.无速度传感器控制永磁直驱风电变流器的研制［J］.电机与控制学报，2009，13(1):67 -72.

［7］ 张友鹏，刘景利，高锋阳，等.永磁直驱风电系统低电压穿越能力仿真［J］.电源技术，2013，37(9):1635 -1637.

［8］ 刘景利，张友鹏，高锋阳，等.永磁直驱风电变流器控制策略及仿真研究［J］.电源技术，2012，36(4):554 -557.

［9］ 徐壮，李广军，徐殿国，等.永磁直驱风电系统发电机侧变流器的并联控制［J］.高电压技术，2010，36(2):474 -480.