无刷旋转变压器的磁路设计及仿真分析

李立娜，李大超，袁永杰

(1.中国电子科技集团公司第二十一研究所，上海200233;2.海军驻上海地区电子设备军事代表室，上海200233)

0 引 言

旋转变压器作为伺服控制系统中的角度位置测量元件，以其精度高、信号强、环境适应性好等特点被广泛应用在航天、航空、船舶、汽车和机械加工等场合。

为提高旋转变压器的可靠性，出现了用环形变压器代替电刷和集电环的无刷旋转变压器。随着粉末冶金软磁合金材料和正弦分布绕组的应用，以及工艺的简化和精度的提高，无刷旋转变压器发展迅速，特别是在宇航等环境要求苛刻的场合被广泛的使用［1］。

1 基本原理

无刷旋转变压器由环形变压器和旋转变压器两部分组成。按照结构形式可分为装配式和分装式，按照环形变压器和旋转变压器的排列方式可分为轴向排列和径向排列，目前广泛使用的是如图1 所示的分装式轴向排列的结构。

电气原理图如图2 所示，其电磁耦合为激磁电源→环形变压器定子→环形变压器转子→旋转变压器转子→旋转变压器定子输出两相cos θ，sin θ 的调制信号。电压方程如下:

式中:UR1R3为环形变压器定子绕组激磁电压;US1S3为旋转变压器定子绕组余弦输出电压;US2S4为旋转变压器定子绕组正弦输出电压;K 为变压比(最大空载输出电压与激磁电压的比);θ 为电气角。

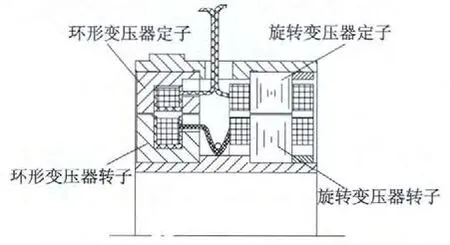
图1 无刷旋转变压器结构图

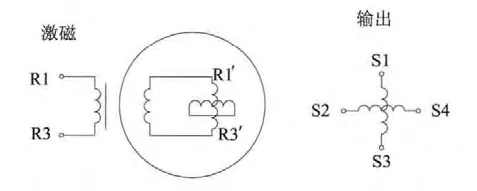
图2 无刷旋转变压器电气原理图

2 磁路法设计

传统的无刷旋转变压器均采用磁路法进行设计，其优点是计算简单，速度快。

下面对无刷旋转变压器磁路计算法进行分析说明。磁路计算法首先根据主要技术指标包括:励磁电压、励磁频率、变压比、外型尺寸等确定环形变压器和旋转变压器的铁心尺寸，再根据阻抗要求对励磁绕组进行计算，根据变压比要求对输出绕组进行计算，最后对环形变压器与旋转变压器对接后的变压比和阻抗进行计算校核，计算流程如图3 所示。

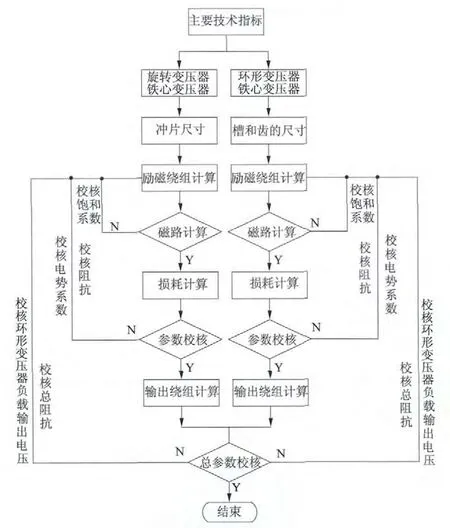
图3 无刷旋转变压器磁路计算流程图

无刷旋转变压器的磁路计算的关键是总参数的校核，即环形变压器与旋转变压器对接后总的输入阻抗和环形变压器的负载输出电压:

式中:Zin为无刷旋转变压器总输入阻抗;Z1k为环形变压器开路输入阻抗;Z2k为环形变压器开路输出阻抗;Zm为环形变压器互阻抗;Zxh为旋转变压器开路输入阻抗;Uhf为环形变压器负载输出电压;U1为无刷旋转变压器励磁电压;Z1r为环形变压器励磁阻抗;Z2r为环形变压器输出绕组串联阻抗;Kw为环形变压器折算系数。

无刷旋转变压器设计的关键参数是精度、变压比和阻抗。虽然磁路法计算可以根据经验比较准确地计算出所需要的冲片尺寸、齿槽分配、结构尺寸等参数，但是由于磁路法是将磁场简化为磁路，并且过多的依赖经验系数，使精度、阻抗和变压比计算并不准确，尤其是无法准确计算出环形变压器磁场对旋转变压器磁场的影响，这就需要通过仿真软件进行电磁场的仿真计算。

3 仿真分析

目前仿真软件很多比如日本JSOL 公司的JMAG，法国Cedrat 公司的Flux 2D 和Flux 3D，美国Ansot 公司的Maxwell 2D 和Maxwell 3D［2］。Ansot公司的Maxwell 软件在电机的仿真计算中被广泛应用，本文采用Maxwell 仿真软件对无刷旋转变压器进行仿真分析。

本文以一款无刷旋转变压器样机为例进行仿真分析，无刷旋转变压器由环形变压器和旋转变压器两部分组成，主要技术参数如表1 所示。定、转子绕组均采用同心式正弦分布绕组。

表1 样机主要参数

采用Maxwell 2D 只能对旋转变压器进行仿真计算，无法分析环形变压器对旋转变压器的影响，因此本文采用Maxwell 3D 进行静磁场和瞬态场的仿真分析。

3.1 静磁场仿真分析

a)模型建立及材料设置

首先在Autodesk Inventor 中建立3D 模型，如图4 所示，导入到Maxwell 3D 中进行参数的设置。

图4 无刷旋转变压器3D 仿真图

b)网格剖分

样机的3D 模型复杂，计算量很大，Maxwell 3D静磁场自适应网格剖分比较合理，因此静磁场不对模型进行剖分，采用自适应网格剖分。

c)静磁场结果分析

通过后处理可以得到无刷旋转变压器的磁场分布情况，图5 为磁密分布图和磁矢量分布图。

图5 无刷旋转变压器磁密分布图和磁矢量分布图

从仿真结果可以看出，环形变压器的漏磁场对旋转变压器是有影响的。为了进一步分析环形变压器对旋转变压器的影响，在模型中对旋转变压器和环形变压器之间建立平面，根据磁通Φ =∫Bds，对平面通过的磁通进行计算。分别计算旋转变压器铁心与环形变压器铁心距离5 mm，7 mm，9 mm 时的截面漏磁通，如表2 所示。

表2 旋变主磁通与环变漏磁通 Wb

从表2 中数据可以更准确的看出，环形变压器磁场对旋转变压器磁场有影响，两铁心近距离时必须采取隔磁措施，通过在环形变压器与旋转变压器之间加隔磁环来减少影响。

3.2 瞬态场仿真分析

为了更准确分析环形变压器对旋转变压器的影响，必须通过瞬态场对旋转变压器输出电压的波形进行分析。瞬态场网格剖分导入静磁场的自适应剖分，励磁加电压源。

a)环形变压器单独仿真

首先对环形变压器单独进行仿真分析，仿真模型如图6 所示，输入、输出电压如图7 所示。

图6 环形变压器仿真模型

图7 环形变压器仿真图

从仿真结果得到电势系数Kh=输出电压/输入电压=0.91，调整副方匝数W2=励磁匝数W1/Kh，调整后的输入输出电压如图8 所示，励磁与输出基本上完全重合。

图8 调整匝数后环形变压器仿真图

b)旋转变压器单独仿真

旋转变压器转子励磁，定子两相输出。仿真模型如图9 所示，得到两相正弦输出电压US2S4、余弦输出电压US1S3，如图10 所示。

图9 旋转变压器仿真模型

图10 旋转变压器输出电压波形

衡量旋转变压器的重要指标是电气精度，即输出电压波形的正弦性。取电压波形曲线最大点做包络线，如图11 所示。在MATLAB 软件中对输出电压包络线做傅里叶分解，得到输出电压各次谐波的数值，并计算出波形畸变率THD(各次谐波均方根值与基值的比)，如表3 所示。

图11 两相输出电压的包络线

表3 输出电压基值与各次谐波的幅值

c)无刷旋转变压器仿真

图12 无刷旋转变压器仿真模型

对环形变压器铁心与旋转变压器铁心距离5 mm 时的无刷旋转变压器进行仿真计算，仿真模型如图12 所示。通过外接电路将环形变压器输出与旋转变压器的输入串接后，得到无刷旋转变压器定子输出正弦相和余弦相，同样在MATLAB 软件中对输出电压包络线做傅里叶分解，得到输出电压各次谐波的数值和波形畸变率，如表4 所示。

表4 输出电压基值与各次谐波的幅值

从无刷旋转变压器的和单独旋转变压器的仿真结果可以看出，环形变压器与旋转变压器布置近距离时环形变压器对旋转变压器输出电压是有影响的，使旋转变压器输出波形的正弦性变差，波形畸变率正弦相增大了1.7 倍，余弦相增大了1.71 倍。在电气精度要求高的场合需要做隔磁处理。

4 隔磁措施

在环形变压器与旋转变压器铁心距离近时可以在两者之间加隔磁环。隔磁环有两部分组成，靠近环形变压器铁心的导磁材料即硅钢片和铜板共同组成，如图13 所示。导磁材料可有效地将环形变压器漏磁感应掉，铜板的相对磁导率为0.999 912，接近空气，可以将未被感应的漏磁通过涡流效应消耗掉。

图13 加隔磁环后无刷旋转变压器仿真模型

加隔磁环后进行静磁场和瞬态场的仿真分析，静磁场中截面漏磁通由6.4 ×10-7Wb 降为2.58 ×10-8Wb，降低24.8 倍。瞬态场仿真，得到的输出电压波形做傅里叶分解，得到两相输出电压的基波和各次谐波值，并计算谐波畸变率THD，如表5 所示。

表4 采取隔磁措施后输出电压基值与各次谐波的幅值

从仿真结果可以看出，采用隔磁措施后无刷旋转变压器的输出电压波形的正弦性有明显改善，接近无环形变压器的结果，因此对精度要求高的产品可以采取此种隔磁措施。

5 试验验证

本文采用与仿真样机相同的参数对无刷旋转变压器进行试验测试，分别进行了单独旋转变压器、无刷旋转变压器未加隔磁和无刷旋转变压器加隔磁三种状态的精度试验。精度试验每隔5°做一点，360°共测试72 点。试验误差曲线如图14、15 和16 所示。

图14 单独旋转变压器误差曲线

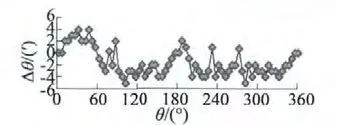
图15 无隔磁措施时无刷旋转变压器误差曲线

图16 有隔磁措施时无刷旋转变压器误差曲线

从三种工作状态的实验数据可以看出，单独旋转变压器时电气误差最好为3＇，无隔磁措施时旋转变压器的电气误差为5＇，采用隔磁措施后旋转变压器的电气误差也为3＇，但误差曲线较单独旋转变压器工作稍差。试验验证了环形变压器对旋转变压器电气精度的影响以及隔磁措施的有效性。

6 结 语

在磁路计算法的基础上，对无刷旋转变压器进行了静磁场和瞬态场的仿真，得出了环形变压器对旋转变压器的影响。瞬态场中分别对环形变压器单独工作、旋转变压器单独工作和无刷旋转变压器工作三种工作状态的输出电压对比分析，得出了环形变压器对旋转变压器输出电压波形的影响程度。

针对环形变压器对旋转变压器的影响，在两铁心距离近时采取隔磁措施，并进行了仿真分析和试验验证，验证了隔磁措施的合理性。

将磁路计算法与电磁场有限元仿真相结合，在准确计算出无刷旋转变压器的主要尺寸、匝数、阻抗等参数的同时，可以仿真计算出无刷旋转变压器的精度，对其他无刷旋转变压器的设计生产有很好的借鉴作用。

［1］ 樊君莉. 控制电机发展综述［J］. 电气技术，2006，(7):50 -53.

［2］ 刘国强，赵凌志，蒋继娅. Ansoft 工程电磁场分析［M］. 北京:电子工业出版社，2005:15 -21.