涡激振动对FPSO外输系统的动态响应分析

洪伟宏

(海军舰船办，北京100073)

0 引言

近年来石油/天然气等开发工程由陆地、近海等浅水区域逐渐转向深水区域，当前在深水海域应用较多的以浮式生产储卸油装置 (Floating Production Storage and Offloading System，FPSO)外输系统为主，并与相应的水下生产系统进行配合开发的深水油气开发工程模式。FPSO外输系统主要包括FPSO、外输油管线和外输浮筒。

在对FPSO外输系统进行初步设计时，随着FPSO不断向更深的海域应用，其所经受的环境载荷也变得越来越复杂，如何模拟浮体和系泊系统之间的耦合作用关系成为设计FPSO外输系统的关键技术点。同时，由于连接FPSO和外输浮筒的外输管线跨距长，在海流作用下外管线的尾流区会产生旋涡现象。若产生漩涡的泄放频率趋近于外输管线的自振频率点，则会出现旋涡泄放频率在一个较大的流速范围内接近于外输管线自振频率的“频率锁定”现象，同时伴随着大幅度振动现象，即“涡激共振”［1］，由此会造成其疲劳损伤，从而会影响FPSO外输系统的使用寿命。

国外学者对FPSO与其系泊系统的耦合作用作了大量研究工作，如 Ran、Garrett［2－3］针对深水和超深水区域作业的船体及其系泊系统，充分算入了船体/系缆/立管的相互作用，研发了时域耦合动力分析研究方法。Tahar［4］采用频域耦合数值模拟和时域耦合数值模拟2种计算方法对深水浮式平台及其系泊系统进行动态响应研究，结果表明时域耦合计算得到的结果比频域计算法更接近实测值。Kim［5－6］基于二项分布Volterra级数展开，对转塔系泊FPSO在非同向风浪流环境力下联合求解船体、系泊及立管的动力性能，其中水动力系数由商业软件WAMIT计算提供。当前，海洋工程领域研究管线水动力性能的方法主要分为计算流体力学模型和经验模型两大类，计算流体力学模型的计算量大、计算时间长且对计算机要求较高，而经验模型如 SHEAR7、VIVA、VIVANA［7－9］等，尽管计算时间相对较短，但基本局限于频域范围内求解。

本文在考虑浮体与管线间的耦合效应的基础之上，计入了外输油管线的涡激振动效应，以准确研究和预测外输油管线的涡激振动现象对整个FPSO外输系统运动响应的影响。基于三维势流理论和快速傅里叶变换法求解浮体在波浪环境下的运动，采用了集中质量法求解了管线张力和弯矩值，选用了涡追踪计算方法对管线建模，涡追踪计算方法基于边界层理论，通过在每个计算时间步内，随机定义众多两个相对独立参考点的位置坐标，由2点的位置坐标形成新的涡而得到管线受到的流体涡激力。此计算模型的优点在于既可用于时域模拟，又能处理管线与浮体的运动耦合问题。

1 理论研究

充分认识其所处的海洋环境特点并准确计算浮体受到的环境载荷是后续准确获得浮体运动响应性能的重要前提条件。本章对浮式结构在作业期间所遭遇的环境载荷进行探讨分析，基本包含风、浪、流、涌浪、飓风等特殊载荷的理论及计算方法。

1.1 浮体的时域运动方程

首先通过频域方法计算，得到浮体的波浪激励力和水动力系数，再通过半解析方法求得时域范围内的波浪激励力、附加质量项以及延迟函数等参数项。在求解浮体时域运动响应时加入双涌浪、飓风、风载荷及流载荷等外力，本文主要采用Newmar kβ法求解计算浮体在时域范围内的总体运动性能。

式中:MS为浮体质量矩阵;Ma(∞)为ω→∞时的浮体附加质量;(t)为浮体加速度，矢量;K为浮体静刚度矩阵;C为浮体阻尼矩阵;F(t)为浮体所受总外力，包括波浪力、流力、风力、飓风、涌浪、系泊力、慢漂力、阻尼力、回复力等等;h(t)为浮体加速度卷积积分函数矩阵。

1.2 管线动力分析

管线在受到外界环境载荷的作用及在系泊浮体运动的扰动下，会产生相应的运动，但此运动具有较强的几何非线性，因此计算系缆的动态运动方程是极为复杂的且与时间有关的强非线性方程，本文基于集中质量法求解了管线的动张力，即是将管线均匀离散成一系列的集中质量点，并采用弹簧将这些节点进行连接并假设弹簧的质量为0，弹簧+阻尼的形式用来模拟管线的弯曲刚度。

图1 集中质量法示意图Fig.1 Sketch of lumped mass method

取图1中外输管线的其中一段加以分析，选3个节点组成2个单元，以单元j为例，加以公式说明。

作用在单元j上的应变能，其计算公式如下:

由此，可以求解得到作用在节点1上的3×3刚度矩阵KA1:

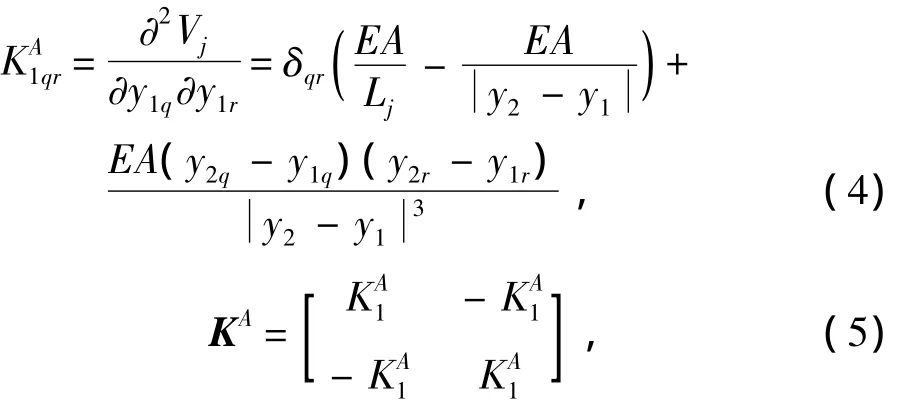
式中，将δqr定义为克罗内克δ函数，即当q=r时，δqr=1;当q≠r时，δqr=0;KA为单元j的刚度矩阵。

假设管线在初始状态处于拉直状态，则存储在旋转弹簧中的势能为:

式中:EI为管线的弯曲刚度;Lk为k单元的管线原长;kb为连接单元j与单元k间等效弹簧的弯曲刚度值;KB为管线的弯曲刚度矩阵。

1.3 浮体与管线的时域耦合数值计算方法

针对浮体与管线的相互耦合效应，将其以相互作用力的形式来处理，此时包含浮体与其系缆的时域耦合运动方程如下:

式中:M为浮体质量矩阵;A为浮体附加质量矩阵;B为浮体阻尼矩阵;K为浮体刚度矩阵;F为作用在浮体上的外力;FM为浮体受到的系泊系统对其的作用力;FOOL为浮体受到的外输油管线对其的作用力，包括管线因涡激振动现象产生的涡激力。

由于管线如系泊系统和外输油管线张力与浮体运动在每时刻都存在相互作用，因而系泊系统和外输管线的张力可以表示成浮体运动的相关函数，即:

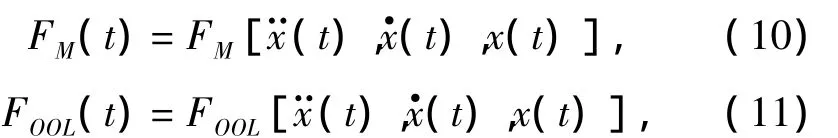
对系泊力和外输管线作用力的处理方式是将其分解为两大类，一类为可表达成与浮体运动相关的显示函数，另一类则为剩下的余项，将作用力与浮体运动相关的显示函数放置于浮体运动方程的左边，而将作用力余项保留在方程的右端，如此，浮体时域耦合运动方程经修正后，表达如下:

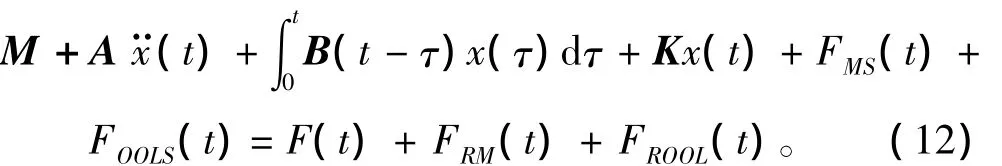
式中:FMS为系缆作用力与浮体相关的显式函数;FOOLS为外输管线作用力与浮体相关的显式函数;FRM为系缆对浮体作用力余项;FROOL为外输管线对浮体作用力余项。

2 数值模型

本文研究的FPSO外输系统，作业水深为1 500 m，FPSO的系泊系统采用4×4的分布式锚链设计，每根锚链均为锚链－钢缆 －锚链的三段组合形式。FPSO的主尺度及其系泊系统的锚链属性详见表1，图2为FPSO的面元计算模型，为准确模拟船体的水动力性能，划分网格时应尽量避免出现三角形单元，最好皆为四边形单元网格，总计4 926个单元，其中水下单元共计2 891个。

图2 FPSO面元计算模型Fig.2 Wave diffraction panel model of FPSO

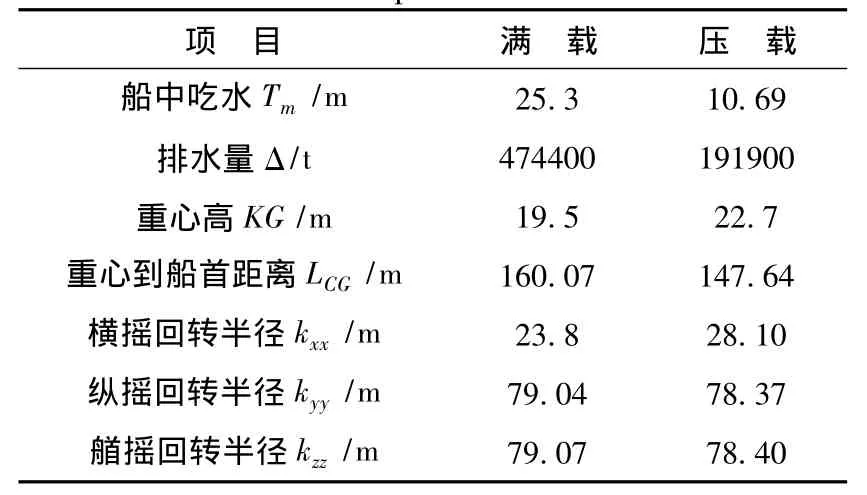
表1 FPSO的主尺度Tab.1 Main parameters of FPSO

图3为FPSO及CALM外输系统在作业的总布置图。浮筒的系泊方式与FPSO有所区别，采用3×3非对称分布式布置，每根系缆均由锚链－钢缆－锚链三段组合构成，每组系缆呈120°夹角，同组锚链缆索间呈5°夹角。表2为外输油管线的主要参数值，表3为海洋环境参数，表4为剪切流的具体参数值。

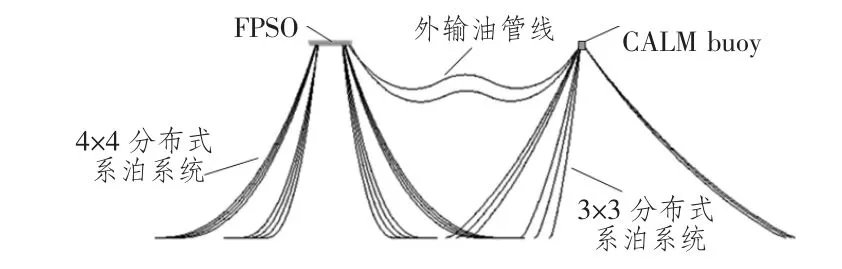
图3 FPSO及CALM外输系统布置图Fig.3 Model of FPSO and CALM offloading system

表2 外输油管线参数Tab.2 Main parameters of oil offloading lines

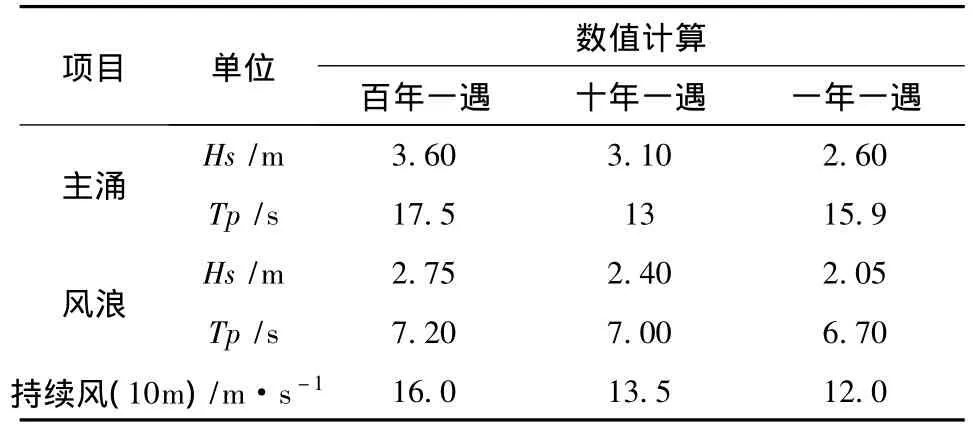
表3 海洋环境条件统计值Tab.3 Parameters of environment condition

表4 剪切流环境条件统计值Tab.4 Parameters of shear current condition

3 结果与讨论

本文将外输管线涡激振动现象与浮体/管线时域耦合运动相结合，计算了外输系统的总体运动响应性能，获得了此现象对多点系泊FPSO及外输浮筒的六自由度运动响应、系缆张力及外输管线张力、疲劳等特性的影响，并对外输管线在设计和布置方面提供了参考性建议。为了阐述方便，将不考虑外输管线的涡激振动效应计为方法A，将考虑了外输管线的涡激振动效应计为方法B，且本文中以左舷外输管线的计算结果为例加以分析。

3.1 外输管线的张力、疲劳特性分析

计入海况条件和环境载荷方向对计算管线疲劳损伤的影响，基于S－N曲线对外输管线进行疲劳特性分析，考虑FPSO及外输浮筒与外输管线的相互作用影响，采用雨流计数法得到输油管各个节点的平均应力、应力幅值和应力循环次数，最后根据Miner线性累计准则来计算变幅应力循环下的疲劳损伤值。

表5 不同海况条件下外输管线张力统计值Tab.5 Line tension results of OOL with different environment conditions

通过分析表5外输管线在不同海况条件下的张力值可发现:外输管线的平均张力值随着海况条件的恶劣程度增加而呈现小幅增加的趋势，方法B计算结果略高于方法A，外输管线的张力均值在管线预张力值附近发生小幅变化。计算结果表明管线涡激振动现象对其管线自身张力的幅值变化影响较为显著，在作业操作时尽量避免管线发生涡激振动的频率范围。

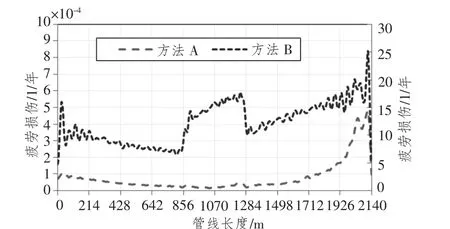
图4 一年一遇海况，管线疲劳损伤值 (左舷)Fig.4 Fatigue damage of OOL with 1－year environment condition(port side)

为了能更加直观的分析管线涡激振动现象对其疲劳损伤的影响，本节以一年一遇作业海况为例，采用方法B得到的疲劳损伤值高于方法A的计算结果，在含有浮力材的管线疲劳损伤值增加的尤为明显，因为含有浮力材的管线部分属于大曲率段，管线因环境外力而产生的涡激力更大导致了其疲劳损伤值的大幅度提升，最高放大了250倍之多。对比方法A和方法B，管线的疲劳损伤值沿着连接FPSO端至外输浮筒的方向呈现逐渐提升的趋势，最大值出现在与外输浮筒的连接处。值得注意的是，方法B计算得到的结果显示了与FPSO连接端的疲劳损伤值出现了极大地突增现象，表明了露出水面段的管线受风的影响造成了管线应力幅值提升，进而加剧了管线的损伤值，即缩减了管线的使用寿命。越靠近浮体端的管线疲劳损伤值起伏变化越大，而靠近外输浮筒端的管线起伏高于靠近FPSO端，表明外输管线的疲劳寿命更易受到小吃水且小水线面浮体运动响应的影响。

图5 15°环境力作用方向下的管线疲劳损伤 (方法A)Fig.5 Fatigue damage of OOL with 15 degree environment direction(Method A)

但在十年一遇海况下，管线的疲劳损伤值分成3个区域，中间区域为带有浮力材的管线部分，每个区域中都出现一个极大值，左舷管线疲劳损伤的最大值发生在管线1 070 m处，最大值为1.8E3，比外输浮筒连接端点的值高出3倍，这是因为1 070 m是左舷管线离自由液面的最近点，因而此点受到的波浪、涌浪及流力作用最大，再加上十年一遇环境载荷频率恰好落在了能激发管线产生共振现象的频率范围内，导致外输管线的疲劳损伤未发生在与外输浮筒连接处，而发生了有3处极大值点的特殊现象。

3.2 多点系泊FPSO运动响应特点分析

考虑外输管线的涡激振动现象，并将此现象与浮体/管线的耦合运动效应相结合，通过时域耦合计算分析，得到多点系泊FPSO的六自由度运动响应和FPSO系缆张力等计算结果。

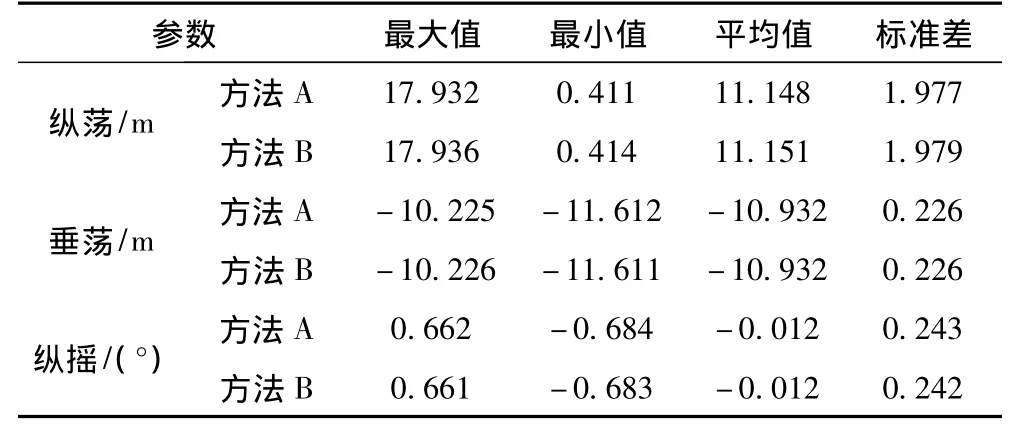
表6 一年一遇海况，FPSO六自由度运动响应统计值 (0°)Tab.6 Dynamic motion of FPSO with the 1－year environment condition(0 degree)

表6为一年一遇海况下FPSO六自由度运动响应统计值。通过分析表6中的计算结果，可发现:方法A与方法B得到的FPSO六自由度运动响应值非常接近，这是因为FPSO与外输管线相比属于大型水线面浮体结构，管线的涡激力对FPSO的作用特别小，再者管线发生涡激力最大的位置距离FPSO较远。总体而言，外输管线的涡激现象对FPSO大型水线面浮体的运动响应影响可忽略不计。

表7 0°环境力作用方向下，FPSO系缆张力统计值Tab.7 Line tension results of FPSO with the 0 degree environment direction

表7给出了方法A和方法B的FPSO系缆张力计算结果，分析表中的数据可发现:计算管线张力均值随着海况条件从一年一遇逐渐增至百年一遇时出现小幅度的增加趋势，对比方法A与方法B计算得到的管线张力均值，方法B略高于方法A，增加的幅值有限，最大不超过0.1%。计算结果表明管线的涡激振动效应对FPSO系缆张力影响较小，可忽略不计。

3.3 多点系泊外输浮筒运动响应特点分析

考虑外输管线的涡激振动现象，并将此现象与浮体/管线的耦合运动效应相结合，通过时域耦合计算分析，得到多点系泊外输浮筒的六自由度运动响应和外输浮筒系缆张力等计算结果。

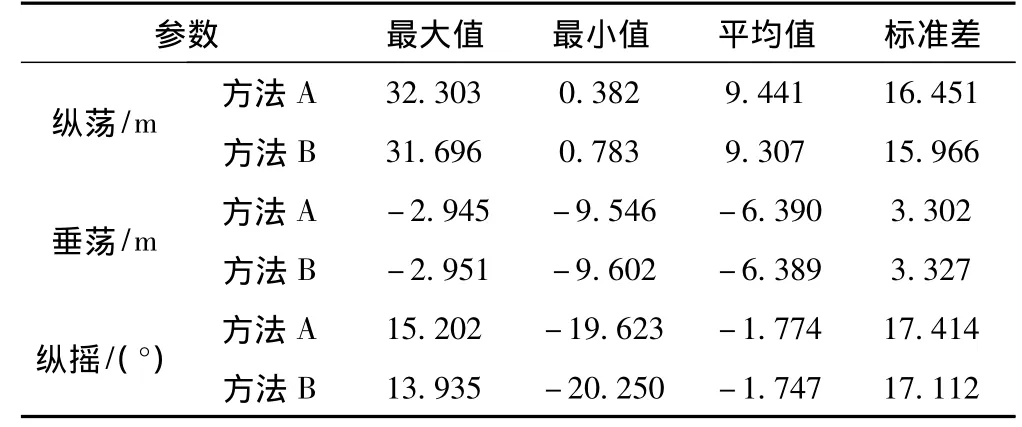
表8 百年一遇海况下的CALM buoy六自由度运动响应统计值 (0°)Tab.8 Dynamic response results of CALM buoy with the 100－year environment condition(0 degree)

表8给出了外输浮筒在不同海况条件下的六自由度运动响应值，分析表中的计算结果可发现:对比方法A与方法B的计算结果，两者的结果较为接近，外输管线的涡激现象对小水线面且小吃水浮体的运动响应影响可忽略不计。

表9 0°环境力作用方向下的CALM buoy系缆张力统计值Tab.9 Line tension of CALM buoy with the 0 degree environment load direction

分析表9中的数据可知:采用方法B得到的系缆张力值高于方法A得到的系缆张力，从系缆张力标准差的角度来看，考虑了管线涡激振动效应，增加了系缆张力的变化幅值，但方法B对系缆均值增加的幅值有限，最大不超过0.16%。计算结果表明了管线的涡激振动效应对CALM buoy系缆的幅值变化存在一定的影响，最大相差不超过13%，而对系缆张力的平均值影响较小，最大不超过0.2%。

4 结语

本文深入考虑了外输管线因距离长受海流作用极易发生涡激振动现象，结合计入FPSO、外输浮筒、外输管线及固定两浮体的系泊系统间的相互耦合作用，结合了三维势流理论、集中质量法和涡追踪计算模型，在时域内求解了整个FPSO及其外输系统的总体运动性能。从浮体运动响应、系缆张力、外输管线张力及其疲劳等方面综合分析了外输管线的涡激振动现象对整个FPSO外输系统的影响。研究发现:

1)在相同环境作用方向下，考虑外输管线涡激振动效应得到的管线张力幅值变化要比不考虑时高出67.81%，而对外输管线张力均值的影响较小，表明了外输管线张力幅值受涡激振动的影响最大。

2)管线的疲劳损伤值在靠近外输浮筒处出现最大值，并随着海况剧烈程度的增加，其发生损伤最大值点逐渐向外输浮筒端偏移，表明了小水线面且小吃水的外输浮筒对管线疲劳损伤的影响较大。同时，管线涡激振动现象会放大等效横截面积和大曲率对疲劳寿命的影响。

3)十年一遇环境载荷频率恰好落在了能激发管线产生共振现象的频率范围内，导致了外输管线的疲劳损伤未发生在与外输浮筒连接处，而发生了三处极大值点的特殊现象，在进行外输作业时应尽量避免与管线自身频率相近的环境载荷。

［1］ 杨明华．海洋油气管道工程［M］．天津:天津大学出版社，1994．

［2］ RAN Z H．Coupled dynamic analysis of floating structures in waves and currents［D］．Doctoral Dissertation，Texas A＆M University，2000．

［3］ GARRETT D L．Coupled analysis of floating production system［J］．Ocean Engineering，2005，32:802 －816．

［4］ TAHAR A，HALKYARD J，LRANI M．Comparison of time and frequency domain analysis with full scale data for the horn mountain spar during squall isidore［C］．Proceedings of the 20th Offshore Mechanics and Artic Engineering Conference，Hamburg，Germany，2006，1:105 －113．

［5］ ARCANDRA T，KIM M H．Hull/mooring/riser coupled dynamic analysis and sensitivity study of a tanker－based FPSO［J］．Applied Ocean Research，2003，25:367 －382．

［6］ KIM M H，KOO B J，MERCIER R M，et al．Vessel/mooring/riser coupled dynamic analysis of a turret-moored FPSO compared with OTRC experiment［J］．Ocean Engineering，2005，32:1780 －1802．

［7］ VANDIVER J K，LI L．SHEAR7 V4．4 Program Theoretical Manual［R］．Cambridge:Massachusetts Institute of Technology，2005．

［8］ TRIANTAFYLLOU M S．VIVA extended user's manual［R］．Cambridge:Massachusetts Institute of Technology，2003．

［9］ LARSEN C M，VIKESTAD K，YTTERVIK R，et al．VIVANA theory manual，version 3．4［R］．Cambridge:Massachusetts Institute of Technology，2005．

［10］罗冬冬，朱仁庆．剪切流下海洋立管涡激振动的三维数值模拟［J］．舰船科学技术，2015，37(2):82 －86．LUO Dong-dong，ZHU Ren-qing．Three dimensional numerical simulation of VIV on marine riser in linearly sheared flow［J］．Ship Science and Technology，2015，37(2):82－86．