水下滑翔机垂直面动力学分析与仿真

张 华，张进峰，张少伟，倪先胜

(1．武汉第二船舶设计研究所，湖北武汉430064;2．东风德纳车桥有限公司，湖北襄阳441000)

0 引言

水下滑翔机是一种依靠机翼水动力和净浮力驱动、将浮标和水下机器人技术结合的新概念水下机器人。水下滑翔机通过间歇性改变自身净浮力和重心在垂直纵剖面的位置从而改变滑翔运动中机翼受到的水动力，借助机翼的升力实现在垂直纵剖面的锯齿状运动，通过重心位置在机翼面的侧向偏移产生的横滚力矩实现机身的横滚，从而使机翼升力产生回转向心力分量实现滑翔机的转向。由于净浮力的改变和重心位置改变是间歇性的，因此滑翔机能耗非常小，适用于长期、大范围海洋环境的长期监测。

1995年以来，在美国海军研究局 (ONR)的资助下，美国研制出了 Slocum、Seaglider和 Spray等［1－3］以电池和海洋温差为能源的水下滑翔机系统，其续航时间一般可达200－300 d，航程达2 000～7 000 km，航行速度约为0.25 m/s。王延辉等［4］设计了基于温差驱动的水下滑翔机，充分利用了海洋温差能，并进行了湖上实验，取得良好效果;赵伟等［5］等设计了滑翔机的浮力调节系统并分析了浮力调节泵的动态性能，通过内置压力传感器准确控制了浮力质量;曾庆礼等［6］从做功的角度规划出滑翔机的最佳路径，并设计出了新型的高速、高效水下滑翔机;程雪梅等［7］介绍了国内外滑翔机研究成果与现状，并探讨了滑翔机在机械结构设计、浮力精确控制等方面的关键技术。

在水动力计算方面，S.Tang［8］设计了无缆水下机器人的水动力拟合仿真实验，采用CFD软件计算了无缆水下机器人在垂直面不同攻角和俯仰角情况下受到的水动力，并将拟合的水动力系数和实际的试验进行对比，验证了拟合结果的有效性;J.S.Geisbert［9］采用USAERO软件计算了滑翔机的附加质量和附加转动惯量，并建立了半物理的实验平台;武建国等［10－11］基于Fluent软件计算了混合驱动水下滑翔器滑翔状态机翼的水动力特性，给出了最大升阻比时对应的攻角，分析并优化了在浅海区水下滑翔器航行效率。马峥等［12］分析了滑翔机的水动力特性与能耗之间的关系，为滑翔机的结构设计和优化提供了条件。胡志强等［13］基于k－ε和k－ω模型，计算分析了CR02水下机器人的水动力系数，并用实际水池拖曳实验验证了系数的可靠性。吴利红等［14］从水动力特性出发对水下滑翔机的主载体线型、升降翼和稳定翼进行优化，为滑翔机的运动控制提供了参考。

在滑翔机垂直面动力学模型与控制分析方面，美国普林斯顿大学N.E.Leonard［15］基于航天飞行器滑翔的原理和模型建立水下滑翔机的动力学模型，给出了水动力在小攻角滑翔情况下的近似表示形式;同时，N.E.Leonard给出了滑翔机在垂直面稳定滑翔情况下净浮力调节、滑翔机重心位置和滑翔机运动状态之间的关系，并基于线性二次最优控制(LQR)，设计了滑翔机在垂直面不同俯仰角下的切换控制方法。J.G.Graver［16－17］用海洋试验数据辨识了Slocum滑翔机水动力参数，确定了精确的升力、阻力系数。葛晖等［18］基于广义的d’Alembert方程推到了变质心控制的水下滑翔机动力学方程，并进行了纵平面下的弹道仿真。王延辉［19］利用吉布斯－阿佩尔方程建立了水下滑翔机的动力学模型，分析了偏心质量块和平移质量块的共同作用对滑翔机三维空间运动和垂直剖面运动的性能的影响。

本文针对某型在研的水下滑翔机原理样机，采用CFX软件计算了滑翔机在不同攻角情况下受到的水动力，并采用最小二乘的方法拟合水动力系数;分析稳态滑翔时，滑翔机控制量和系统状态量之间的关系;基于LQR方法，设计滑翔机在不同俯仰角的稳态运动状态之间的切换控制方法。

1 水下滑翔机工作原理介绍与动力学模型

1.1 水下滑翔机工作原理

本文将滑翔机载体质量分为3个部分:内部姿态调整的动质量块mmr。滑翔机壳体静质量mrb和浮力调节质量mb，滑翔机各部分质量和转动惯量的含义如表1所示。建立如图1(a)所示的动坐标系e0(e1，e2，e3)和惯性坐标系 E0(i，j，k)，质量块 mmr沿e1移动可改变滑翔机载体重心在e1轴上的位置，实现载体垂直面的锯齿形运动;当mmr绕e1转动γ角时，可以改变滑翔机载体重心在e2轴上的位置，使滑翔载体回转以实现偏航 (本文暂不讨论偏航)，通过改变载体浮力mb的大小来实现滑翔机的下潜和上浮。由于滑翔机稳态下绕e2轴的力矩为0，因此滑翔机载体壳体静质量mrb及其位置rrb确定了滑翔机动质量块mmr初始平衡位置rmr。

表1 水下滑翔机符号表示形式与含义Tab.1 The symbol definition for underwater glider

图1 滑翔机系统质量分布与跟踪误差定义Fig.1 The mass distribution and error definition of glider

滑翔机受到的净浮力为:

当净浮力为正时，滑翔机往下滑翔，反之，滑翔机往上滑翔。通常当浮力一定时，滑翔机系统的重心在不同的位置，可使滑翔机以不同的俯仰姿态滑翔。同时，在滑翔机俯仰姿态一定的情况下，改变滑翔机的净浮力的大小可改变滑翔机的运动速度。因此需建立动质量块在不同位置、滑翔机载体在不同净浮力情况下载体的稳定运动状态之间的关系，并深入分析载体的质量配置和浮力变化对滑翔机动力学系统的影响，以确定滑翔机滑翔工作状态的范围以及系统稳定性。

1.2 水下滑翔机动力学模型与稳态分析

结合滑翔机的特性，并基于文献［10］的模型，给出水下滑翔机的动力学模型用以分析动质量块沿e1方向移动的情况下的控制。

动坐标系下滑翔机的前向速度、垂向速度、角速度和俯仰角分别为 V1，V3，q，θ，滑翔机在惯性坐标系下的位置和速度分别为x，z，Vx，Vz，控制输入为动质量块受到推力UFmr1和浮力变化率，P1为动质量块的动量。滑翔机在动坐标系下的速度和攻角关系为:

式中的升力L、阻力D和回转力矩M可近似表示为［10］:

滑翔机大部分时间都工作在稳定运动的滑翔状态中，此时滑翔机载体状态量 V1，V3，rmrx，P1，mb为常值，俯仰角速度q=0。当水下滑翔机在垂直面做直线滑翔运动时，滑翔机动力学系统状态量=，所以式可以简化为:

由上式可求得在稳定状态下电池质量块在e1方向上的位置:

定义航迹角为σ=θ－α(见图1(a))，可以将式化简为

展开式(8)，由于V不为0，消去V化简可得到

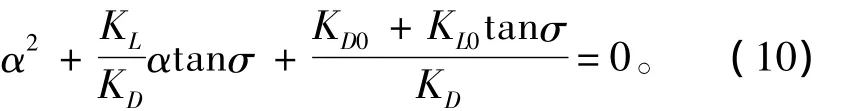
在α有解的情况下，可得到:

对应可求得σ的范围为

式中正号和负号分别代表向上滑翔和向下滑翔的2种情况。

在满足的情况下，合理选取σeq，可以求得相应的攻角:

在已知αeq后，消去mb可求出滑翔机的俯仰角为

将sin2σ+cos2σ=1代入式中消去σ，可得滑翔机的合速度为:

2 水下滑翔机垂直面控制方法

本节给出了在浮力一定的情况下，通过改变rmrx使滑翔机在不同的俯仰角下滑翔的切换控制方法。为分析方便，定义滑翔机的跟踪误差z'，如图1(b)

所示。

由图1(b)可知，z'垂直于期望轨迹，并量测了该方向上的误差，当z'=0时，滑翔机滑翔到期望的轨迹上。

取状态量为X=［z' θ V1V3q rmrxP1¯m］T，取控制输入量为动质量块受到的推力和滑翔机净浮力的变化量，即U=［UFmr1ub］T，联立式和中对应的状态方程量，可得

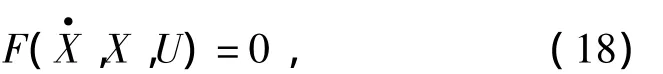
对式(18)线性化，可得

A，B矩阵中各元素值如下:

对线性化后的状态方程，采用LQR控制方法设计控制律，分析滑翔机在不同状态下的切换。LQR是一种标准的二次线性最优控制，选取控制状态的变化量和控制量的变化量的平方作为性能函数，通过给定控制量和控制状态之间的权重函数，确保系统控制量的变化和控制状态之间的变化在实际机械系统允许范围情况下，设计一个局部的稳态控制器。通常性能函数选取为:

式中Q，R为权重矩阵，通过合理选取Q，R，结合滑翔实际的运行状态，使滑翔机在切换过程中的控制量和状态量在滑翔机机械结构设计、净浮力变化允许的范围内。

3 滑翔机垂直剖面运动控制仿真

3.1 水下滑翔机水动力计算与分析

本文基于k－ε模型，采用Gridgen软件和CFX软件设计了滑翔机在垂直面的拖曳水池数值模拟实验。建立的数值流域模型为如图2所示的长方体流域:长5Ll，宽18LD，高18LD(Ll，LD分别是水下滑翔机主体的长度和最大直径)，流域的纵向与滑翔机的主轴e1向成一定攻角，水下滑翔机在载体坐标系下的各线速度满足如下关系:

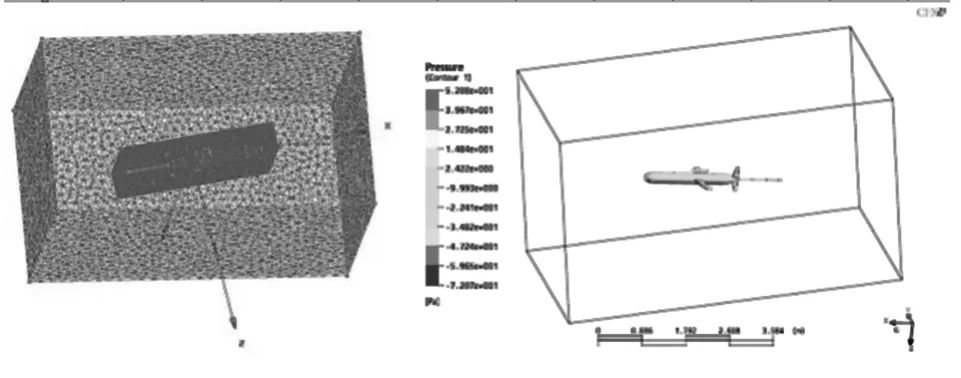
图2 滑翔机垂直面水动力计算Fig.2 The hydrodynamic calculation for glider

由于滑翔机在垂直面稳态滑翔时，漂角β=0，攻角α较小，因此在同一来流速度V=0.5 kn下，计算攻角在－12°≤α≤12°情况下滑翔机在垂直面受到的力和力矩。升力L、阻力D和回转力矩M采用最小二乘法拟合，拟合结果与CFX计算结果如图3所示，拟合结果和计算数据比较吻合。对应水动力系数为

3.2 水下滑翔机垂直面切换控制分析

图4 平衡滑翔状态时，速度关系和攻角俯仰角之间关系Fig.4 The variation between speed and angles

选取LQR控制器权重为

图5 滑翔机载体速度V1、V3，俯仰角θ和角速度q的变化Fig.5 The variation between time and speed，angles

图6 滑翔机载体动质量块位置、浮力的变化及跟踪误差Fig.6 The variation between time and position，buoyancy，error

相对应的控制律为U=－KΔX，通过解关于A，B，Q，R的黎卡提方程可以得到返回控制量K，通常使滑翔机的俯仰角变化、浮力变化量、动质量块的速度的变化波动较小，因此相对应的权重较大。图5和图6给出了Matlab的仿真结果，控制量和滑翔机载体的状态量均在机械结构允许范围内。在t=800 s，1 600 s，2 400 s，3 200 s时，滑翔机在这2个状态之间切换。从仿真中可知，系统的各个状态波动较小，切换过程较为平稳，且动质量块的移动量和浮力质量的变换都在滑翔机机械系统允许的范围内。

4 结语

本文介绍了水下滑翔机在垂直面的水动力计算方法和垂直面的稳态分析过程，并基于LQR方法，给出了滑翔机在垂直面不同俯仰角的切换控制策略。通过合理选择LQR控制器的权重，可使滑翔机在不同滑翔状态间切换时，滑翔机的状态量变化在滑翔机动力系统允许范围内，并保证动质量块的控制量和浮力的控制量的变化也均在实际机械系统可允许的范围内，仿真表明了这种控制方法的有效性。

［1］ WEBB D C，SIMONETTI P J，JONESC P，SLOCUM，an underwaterglider propelled by environmental energy［J］．Oceanic Engineering，2001，26:447 －452．

［2］ SHERMAN J，DAVISR E，OWENSWB，et al．The autonomousunderwater glider“Spray”［J］．Oceanic Engineering，2001，26:437 －446．

［3］ ERIKSEN CC，OSSE T J，LIGHT R D，et al．Seaglider:A long rangeautonomous underwater vehicle for oceanographic research［J］．OceanicEngineering，2001，26:424 －436．

［4］ 王延辉，王树新，谢春刚．基于温差能源的水下滑翔器分析与设计［J］．天津大学学报，2007，40(2):133 －188．

［5］ 赵伟，杨灿军，陈鹰．水下滑翔机浮力调节系统设计及动态性能研究［J］．浙江大学学报(工学版)，2009，43(10):1772－1776．

［6］ 曾庆礼，张宇文，赵加朋．水下滑翔机总体设计与运动分析［J］．计算机仿真，2010，27(1):1 －6．

［7］ 程雪梅．水下滑翔机研究现状进展及关键技术［J］．鱼雷技术，2009，17(6):1 －6．

［8］ TANG S，URA T，NNKATANI T，et al．Estimation of the hydrodynamic coefficients of the complex-shaped autonomous underwater vehicle TUNA － SAND［J］．Journal of Marine Science and Technology，2009，14:373 －386．

［9］ GEISBERT J S．Hydrodynamic modeling for autonomous underwater vehicles using computational and semi-empirical methods［J］．Master Thesis，Virginia Polytechnic Institute and State University，2007．

［10］武建国，陈超英，王树新．混合驱动水下滑翔器滑翔状态水动力特性［J］．天津大学学报，2010，43(1):84 －89．

［11］武建国，陈超英，王树新．浅海水下滑翔器航行效率分析［J］．中国机械工程，2009，3(20):349 －353．

［12］ MA Zheng，ZHANGHua，ZHANGNan，MA Dong-mei．Study on energy and hydrodynamic performance of the underwater glider［J］．Journal of Ship Mechanics，2006，10(3):53 －60．

［13］胡志强，林扬，谷海涛．水下机器人粘性类水动力数值计算方法研究［J］．机器人，2007，29(2):145 －150．

［14］吴利红，俞建成，封锡盛．水下滑翔机器人水动力研究与运动分析［J］．船舶工程，2006，28(1):12 －16．

［15］ LEONARD N E，GRAVER J．Model-based feedback control of autonomous underwater gliders［J］．Oceanic Engineerng，2001，26:633 －645．

［16］ GRAVER J G，LEONARD N E．Underwater glider dynamics and control，12th international symposium on unmanned untethered submersible technology，2001．

［17］ GRAVER J G．Underwater gliders:dynamics，control and design［J］．Phd Thesis，Princeton University，2005．

［18］葛晖，徐德民，周秦英．基于变质心控制的低速水下航行器动力学建模［J］．机械科学与技术，2007，26(3):327 －337．

［19］王延辉．水下滑翔器动力学行为与鲁棒控制策略研究［D］．天津:天津大学，2007．