一种改进的基于GPS某型舰船姿态解算算法

孙海文，欧阳中辉，王 彦

(海军航空工程学院兵器科学与技术系，山东烟台264001)

0 引言

现在利用载波相位技术进行定位是十分活跃的研究领域，由于GPS L1载波波长很短，只有19 cm，载波相位测量噪声很小，因此测量精度高，能达到很高的定位精度。对此许多人作了研究，并将此技术应用到姿态测量领域［1－3］。

利用载波相位GPS进行测姿已逐渐应用于卫星、导弹、飞机、船舶、汽车等高动态的载体上［4－6］。随着载波相位 GPS测量精度的不断提高，利用其动态测量精度高、实时性好、受环境影响小的特点［7－8］，可以对舰船进行海上动态标校。目前对于姿态解算算法有很多，例如九参数最小二乘法、三参数迭代最小二乘法、直接算法［8］等。前2种算法的优点是，可利用多条基线的冗余信息，解算精度较好，但计算过程复杂，实时性差;直接算法通过代数方法求解载体的姿态角，其原理简单易懂、计算速度快、实时性好，在单基线解算中，其解算精度较好，但在解算中没有对粗大误差和GPS信号缺失进行处理，解算结果误差较大。

1 舰船姿态角定义

舰船姿态角一般是指船舶甲板坐标系相对当地水平坐标系之间关系的角度，姿态角，为纵摇角(P)、横摇角(R)、航向角(Y)。用坐标系O－XYZ来表示水平坐标系［9］，姿态角定义如图1所示。

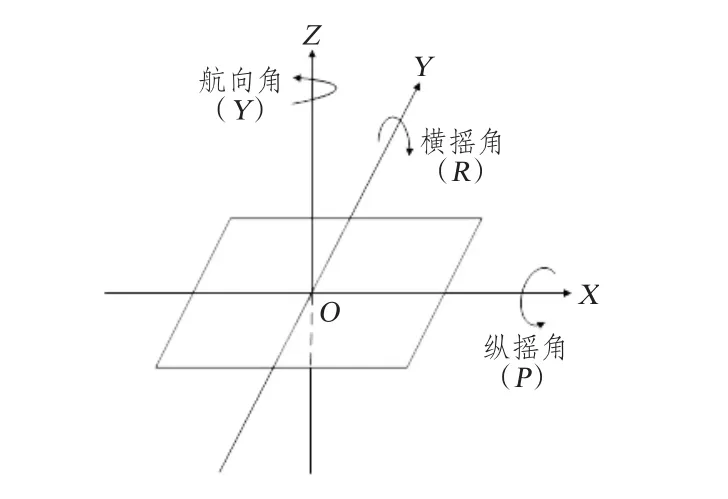
图1 姿态角示意图Fig.1 The attitude angle diagram

舰船相对于水平坐标系X轴的相对旋转角度定义为纵摇角，右手定则X轴正方向沿着手指方向转为正，否则为负;Y轴的相对旋转角度定义为横摇角，右手定则Y轴正方向沿着手指方向转为正，否则为负;Z轴的相对旋转角度定义为航向角，右手定则Z轴正方向沿着手指方向转为正，否则为负。

2 直接算法

直接计算法是根据基线的当地水平坐标值和舰船甲板坐标值及两坐标系间的转换关系直接求解载体姿态角的算法。在单基线测量时只能求解出航向角和纵摇角。在船的首尾分别安放GPS接收机，尾部的接受机为基准站天线1，首部的接收机为用户站天线2，GPS接收机架设坐标系如图2所示，天线1和天线2之间的连线经过甲板坐标系原点且位于舰船甲板坐标系的Y轴上。天线1和天线2之间的连线向量记作L12，这条基线的长度和方向可精确测量。

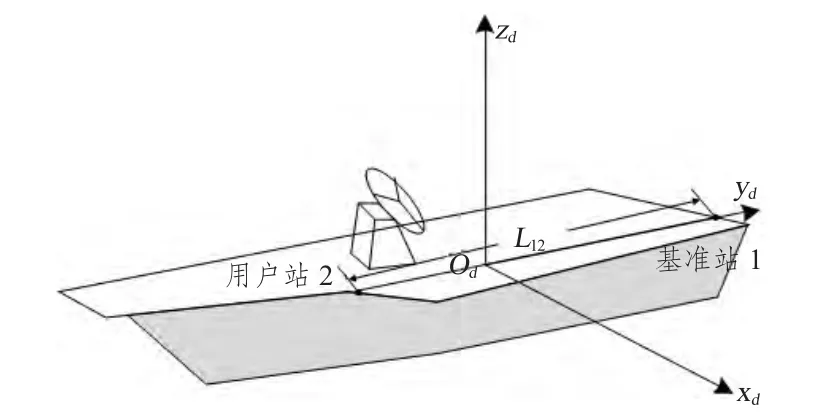
图2 甲板GPS架设示意图Fig.2 The deck GPSerection diagram

直接计算法的具体计算过程如下:

第1步:根据GPS精密单点定位方式测量出基准站的地心坐标，同时利用GPS的载波相位差分方式测量出用户站相对于主天线在地心坐标系下的基线解:

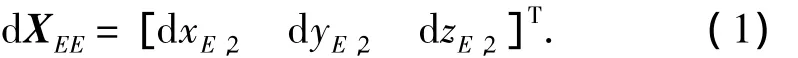
其中E为地心坐标系。

第2步:按照式(2)把式(1)地心坐标系下的解转换成当地水平坐标系下的解:

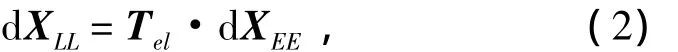
式中:L为当地水平坐标系;l0和b0分别为舰船甲板坐标系原点的经度和纬度。

第3步:根据当地水平坐标系与舰船甲板坐标系之间的转换关系［10－11］，如图3所示，可以得到坐标转换关系式:

其中D为舰船甲板坐标系。

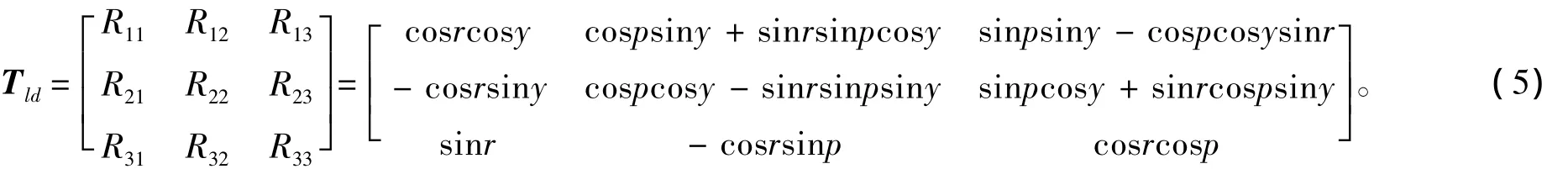
图3 当地水平坐标系和舰船甲板坐标系间的转化示意图Fig.3 Conversion diagram of the local level coordinate system and the ship deck coordinate system

第4步:把基L12线的当地水平坐标系的解d XLL=［d xL，2d yL，2d zL，2］T和舰船甲板坐标系的解 d XDD=［0 L120］T同时代入式(4)，得:

由式(6)可解得:

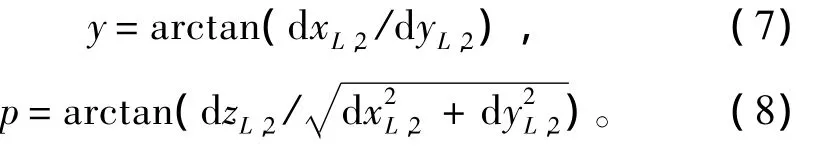
对式(7)进行微分，得到:

航向角的方差为

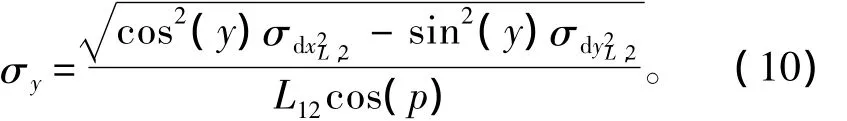
上式化成不等式为

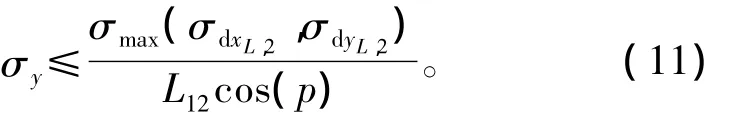
σdxL，2，σdyL，2为 GPS 接收机的测距精度，统一用σΔGPS来表示，即为:

由上述公式分析可知，航向角的精度与定义航向的基线L12的长度成反比，即基线长度越长，精度越高，此结论只适用于短基线 (一般在10 km范围内)。

在解算纵摇角时基线在Z轴的投影长度较短，因此其解算精度较低。

3 基于自适应卡尔曼滤波的姿态解算算法

为满足舰船姿态的实时测量需求，本节提出一种不受粗大误差干扰和GPS信号短暂缺失的GPS定姿算法。该方法的基本原理和解算过程如下:

在姿态测量开始前，通过GPS静态相对定位方式确定出用户天线相对于基准天线在载体坐标系下的基线d XkD2，其中k为历元号;

舰船姿态测量过程中，根据伪距单点定位方式或伪距差分方式获得基准天线的地心坐标值。同时，利用载波相位差分方式获得用户天线相对于基准天线的基线向量(地心坐标系)，见式(1);利用旋转矩阵将上述地心坐标系下的解转换成当地水平坐标系下的解:

再利用旋转矩阵Tkdl，得到基线当地水平坐标系下的解与载体坐标系下解得函数关系式:

其中r，p，γ分别为翻滚角、俯仰角和航向角。

式(15)是以r，p，γ为未知量的非线性表达式。用自适应卡尔曼滤波进行参数估计前需先进行线性化处理，把式(14)进行泰勒级数展开并保留第一项，可得到式(14)的线性化表达式:

式中:∑dXkL，2为的协方差矩阵;Vk为残差。由于是单基线测量，在解算过程中横摇角r会为0。利用直接算法获取初始解p0和γ0。

对于单基线，则其最小二乘解及协方差为:

在舰船的姿态测量过程中，舰船始终处于摇摆状态，所以可根据前一历元的信息和舰船的摇摆方程，来预测和估计下一历元的信息。由于舰船的摇摆运动是不规则的曲线，采用加速度模型时会出现周期的间断点，所以此处采用常速度模型，有:

其中，

式中:Xk和分别为历元k的真值和估计值;Φk/k－1为状态转移矩阵;Wk为动态噪声;Δt为历元间隔;ω为姿态角变化的速度;Q为姿态角变化的速度功率谱密度。

那么，基于常规卡尔曼滤波的递推解为:

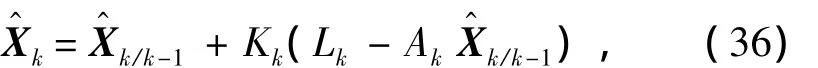
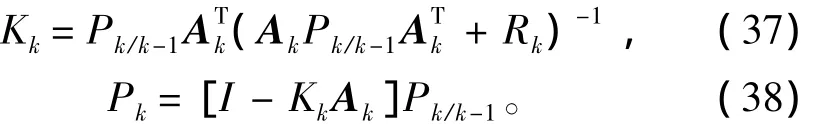
进一步，可写出基于自适应卡尔曼滤波的解为:

其中α为自适应因子，它们的计算公式如下:

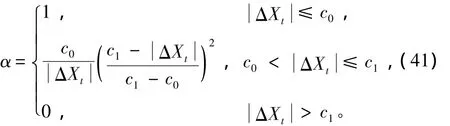
式中:c0和c1为常数，一般取值范围为c0=1.0～1.5，c1=3.0～4.5。ΔXt按下式求取:

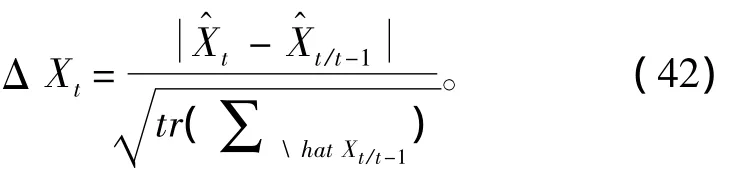
4 仿真试验

4.1 仿真条件建立

假设2个组GPS数据基准站为 (E37.94169444，N121.6988889)、 用 户 站 为 (E37.94166666，N121.6975000)、高度为15 m，坐标原点位于用户站与基准站之间连线上坐标为 (E37.94168750，N121.6985417)。

建立舰艇纵摇角模型

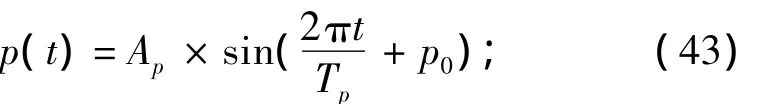
航向角模型

纵摇角速度模型

航向角速度模型

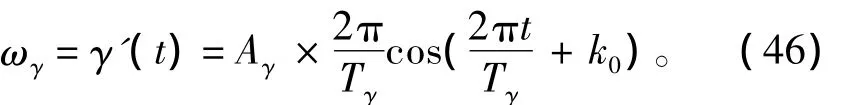
式中:Ap，Aγ分别为舰船的纵摇角幅度值和航向角幅度值;Tp，Tγ分别为舰船纵摇周期、舰船偏航周期;p0，k0分别为舰船纵摇角初始相位、舰船偏航角初始相位;γ0为舰船航向角;¯ωp，¯ωγ为舰船引入误差后的角速度。

4.2 纵摇角和航向角误差比较

图4是引入误差后，纵摇角和航向角的测量误差和标准差的曲线图。

图4 纵摇角误差和航向角误差曲线图Fig.4 The curves of the pitch angle error and the path angle error

从图4可看出，航向角误差值的标准差小于纵摇角误差值的标准差，而且相差一个数量级，因此得出结论，在单基线测量过程中纵摇角测量精度明显低于航向角测量精度。

4.3 航向角误差与基线长度的关系分析

通过经纬度数据可计算出2个GPS天线之间的距离为122 m;保持纬度不变，缩小经度之间的差值，基线长度分别为73 m和24 m。仿真结果如图5所示。

图5 不同基线长度下误差情况曲线图Fig.5 The curves of different baseline length errors

从图5可看出，随着基线长度缩短，测量误差的标准差逐渐增大。因此可知，在短基线 (一般在10 km以内)情况下，航向角的测量精度跟基线长度有关系，基线越长，精度越高。

4.4 直接姿态解算算法和基于自适应卡尔曼滤波的姿态解算算法比较及分析

第1步:仿真出用直接算法解算出的航向角与真实航向角对比曲线图，并仿真出误差曲线图如图6所示。

图6 直接算法解算与真值比较及误差曲线图Fig.6 The comparison of the solution of the direct attitude algorithm and the true value curves and the error curves

第2步:仿真出改进算法解算出的航向角与真实航向角对比曲线图，并仿真出误差曲线图如图7所示。

图7 改进算法解算与真值比较及误差曲线图Fig.7 The comparison of the solution of the improved algorithm and the true value curves and the error curves

第3步:为了更直观地看出改进算法的优势，将改进算法、直接算法与真值进行比较，如图8所示。

图8 改进算法、直接算法与真值比较图Fig.8 The comparison diagram of the improved algorithm，the direct algorithm and the true value

第4步:对2种算法的误差进行仿真比较，绘出误差曲线并计算出误差的标准差，如图9所示。

图9 两种算法的误差对比图Fug.9 The error comparison diagram of the two algorithms

从仿真图中可看出，改进后的姿态测量算法能很好地消除粗大误差，并能很好地补偿缺失数据，测量的姿态角精度明显提高。计算出的改进算法的误差标准差=0.001 2，明显小于直接算法的误差标准差=0.034 4，相差一个数量级，解算精度得到明显提高。

5 结语

本文对直接法求解姿态角进行公式推导，因为直接算法在解算过程中，不能消除粗大误差并且受GPS信号缺失的影响，因此提出了一种改进的姿态角解算即基于自适应卡尔曼滤波的姿态解算算法;通过仿真试验分析比较航向角与纵摇角的测量精度、航向角与基线长度的关系、直接法与基于自适应卡尔曼滤波的姿态解算算法的测量精度，仿真结果表明航向角的解算精度比纵摇角的解算精度高，且高出一个数量级;基线越长，航向角测量精度越高;改进算法比直接算法的解算精度高，且高出一个数量级。

［1］ 李跃，邱致和．导航与定位［M］．北京:国防工业出版社，2008:192－193．

［2］ ELLIOTT D K．Understanding GPSprinciples and applications artsch house［D］．1996．

［3］ ZHU R，SUN D，ZHOU Z Y，et al．A linear fusion algorithm for attitude determination using lowcostMEMS－based sensors［J］．Measurement，2007，40(3):322 －328．

［4］ 韩慧群．GPS姿态测量系统研究与开发［D］．哈尔滨:哈尔滨工程大学，2005．

［5］ CHANG X W，YANG X，ZHOU T Y．et al．A modified lambda method for integer least-squares estimation［J］．Journal of Geodesy，2005，79(2):552 －565．

［6］ 黄显亮，温连峰，王强．基于多天线GPS舰船姿态测量系统研究［J］．舰船电子工程，2009，29(12):80 －82．HUANG Xian-liang，WEN Lian-feng，WANG Qiang．Study on multi antenna GPS ship attitude measurement system based on the［J］．Ship Electronic Engineering，2009，29(12):80－82．

［7］ 杨铁军．GPS实时姿态测量技术与多径误差研究［D］．成都:电子科技大学，2003．

［8］ 李俊毅．GPS姿态测量及相关技术的研究［D］．南京:信息工程大学，2004．

［9］ 李哲，苏秀琴，乔永明，等．基于船姿测量的舰载光电经纬仪视轴稳定方法研究［J］．光子学报，2009，38(6):1553－1556．LI Zhe，SU Xiu-qin，QIAO Yong-ming．et al．Shipboard theodolite LOS stabilization based on ship attitude measurement［J］．Acta Photonica Sinica，2009，38(6):1553－1556．

［10］杨铁军，张晓玲，付毓生，等．基于DSP的GPS双天线实时姿态测量系统实现［J］．电波科学学报，2002，17(6):661－666．YANG Tie-jun，ZHANG Xiao-ling，FU Yu-sheng，et al．Realize the real-time attitude determination system of GPS dual antenna based on DSP［J］．Chinese Journal of Radio Science，2002，17(6):661 －666．

［11］黄德武．GPS变形监测中多路径效应影响研究［D］．成都:西南交通大学，2005．