基于演化算法和讨价还价博弈的多目标最优潮流研究
付艳兰,赵雪霖,刘铠诚,何光宇
(1.海南电网公司,海口市 570273;2.电力系统国家重点实验室(清华大学电机系),北京市 100084; 3.上海交通大学电机系,上海市 200240)
基于演化算法和讨价还价博弈的多目标最优潮流研究
付艳兰1,赵雪霖2,刘铠诚2,何光宇3
(1.海南电网公司,海口市 570273;2.电力系统国家重点实验室(清华大学电机系),北京市 100084; 3.上海交通大学电机系,上海市 200240)
针对电力系统的多目标最优潮流问题,首先通过遗传算法取得帕累托解集,从而充分反映出不同优化目标之间相互影响、相互背离的内在关系,在此基础上利用纳什讨价还价博弈方法选取全局最优解。探讨同时考虑发电费用(或发电煤耗)最小和系统网损最小的多目标最优潮流问题,首先验证该问题满足讨价还价博弈公理,再通过强度帕累托演化算法(strong Pareto evolution algorithm 2, SPEA2)求解得到帕累托前沿,保证收敛速度较快且帕累托前沿分布均匀,最后基于纳什讨价还价博弈求得最优解,解决了不同目标函数之间可能存在的矛盾。该文通过对IEEE 14节点系统的算例计算,验证了该方法的有效性。
多目标;最优潮流;纳什讨价还价博弈;遗传算法
0 引 言
电力系统最优潮流是通过对控制变量的优化选择,在满足系统所有约束条件的前提下,使得系统运行效益的某一给定的目标函数最优[1-2]。由于电力系统单独优化上述某一运行效益(如单独优化发电成本或单独优化系统网损)时,都不一定是系统的最佳运行方式,只有同时优化多个目标时才更具有实际意义,因此许多学者针对多目标最优潮流计算做出很多研究,并取得了开创性的研究成果,如文献[3-4]同时考虑机组燃料费用和系统有功网损为目标函数情况下的最优潮流计算,文献[5-6]则以有功网损和发电总耗量为目标函数进行多目标最优潮流计算。
求解多目标最优潮流问题一般先将多目标优化问题转化为单目标优化问题,再进一步求解该单目标优化问题。如文献[7]引入模糊集理论将多目标优化问题转化为单目标优化问题,再进一步与免疫禁忌混合算法相结合进行求解。文献[8]利用目标满意度的隶属度函数概念进行目标的多对单转化,并采用内点法求解。然而这些转化方法都没有充分反映出不同优化目标之间的相互影响、相互背离的内在关系,如要获得更小的发电成本,必然使成本系数低的机组更多出力,从而破坏了系统整体稳定性,即经济性与稳定性难以兼顾。文献[9]在非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA)的基础上,采用NSGA-II[10]算法,获得优质广泛的帕累托前沿,反映出了多目标优化的不同目标之间相互矛盾的关系,但文章认为最终需要决策者根据实际情况从帕累托解集中选择需要的方案,而未能给出更为充分的分析和更有说服力的结果。因此,本文首先采用遗传算法中的强度帕累托演化算法(strong Pareto evolution algorithm 2, SPEA2)[11]求解多目标优化的帕累托前沿,充分反映出不同优化目标间的内在关系,再进一步引入博弈的思想,将不同的优化目标视为博弈者,各优化目标间的协调过程则可视为博弈者之间的讨价还价过程。若此博弈过程满足Nash公理,则可求出该博弈问题的唯一解,从而使最优潮流在发电成本和网损等不同的优化目标间取得平衡。
1 多目标最优潮流模型
本文建立的多目标最优潮流模型中同时考虑了2个目标:发电费用(或发电煤耗)最小;系统网损最小。目标函数如(1)式和(2)式所示:
(1)
(2)
约束条件:
(1)潮流方程:
(3)
(2)发电机节点有功上下限约束:
(4)
(3)发电机节点无功上下限约束:
(5)
(4)节点电压的上下限约束:
(6)
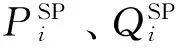
2 基于讨价还价博弈的算法
上述多目标最优潮流模型希望能同时优化“发电费用”和“网损”这2个指标。这2个指标相互联系、相互影响,既不完全一致,也不完全背离。从数学上看,二者实质存在着某种“竞争-合作”关系。因此将“发电费用”和“网损”看作2个互相竞争的谈判单位所追求的目标,它们可选择的策略就是发电机节点的有功功率和电压控制。因此,采用博弈论中的讨价还价博弈方法解决这个问题。
2.1Nash公理模型
在讨价还价过程中,假设利益双方都是理性的,且对于对方可能的策略及收益有着完全的了解。对于这类讨价还价问题,Nash提出了4条公理,用于求出一个博弈双方都可以接受的“合理”的解。下面对这些公理及其意义进行阐述,并验证该多目标最优潮流模型满足这4条公理。
(1)帕累托有效性:一个双方均可接受的结果不能被其他结果所“优超”,即不能有其他结果使双方均获得更大的收益。即讨价还价博弈问题的结果一定在其所对应的多目标优化问题的帕累托前沿上。在该多目标最优潮流模型中,将“发电费用”和“网损”看作2个互相竞争的谈判单位所追求的目标,一个双方均可接受的结果,一定不能有其他的结果既获得更少的发电费用又获得更少的网损,即该讨价还价问题的结果一定在其所对应的双目标优化问题的帕累托前沿上。
(2)对称性:对称性是指博弈方的讨价还价结果与双方决策的顺序无关,只由博弈双方的收益函数决定。即当博弈方收益空间完全相同时,作为2个理性的对局者,没有理由不对等地分配它们的收益。在该多目标最优潮流模型中,讨价还价结果与发电费用和网损的决策顺序无关,满足对称性。
(3)等价收益的不变性:对任一方的收益函数作线性变换,则最终合理解也应做同样的线性变换。这一公理表明了博弈双方合理解的相对位置不随收益数值大小的改变而改变。对该多目标最优潮流模型,无论对发电费用还是网损作线性变换,最终合理解也都是做同样的线性变换,故满足等价收益的不变性。
(4)无关选择的独立性:假设U和U′是2个讨价还价问题,U′的收益空间是U的收益空间的子集,则U的合理解必然也是U′的合理解。即对博弈者来说,在选择某个合理解的时候,与合理解无关的选择不会影响最终博弈的结局。对该多目标最优潮流问题,假设约束条件变化,形成讨价还价问题1和讨价还价问题2,如果讨价还价问题2的收益空间是讨价还价问题1的收益空间的子集,那么问题1的合理解必然也是问题2的合理解。该讨价还价问题满足无关选择的独立性。
Nash证明了在满足上述公理的前提下,讨价还价问题存在下述唯一的合理解:
(7)
式中:f1、f2为博弈双方的收益函数,(d1,d2)表示博弈双方可能会得到的最差收益。一般来讲,若双方都是理性的博弈者,且均对自身利益有着相同的偏好程度,则它们总是希望选择一个离最坏情况最远的解,因而两人谈判的结果即为最终的博弈解。
2.2 基于讨价还价博弈的多目标最优潮流模型
对于发电费用和网损这2个目标,采用讨价还价问题模型求解Nash均衡解,则可等价于求解下述二次优化问题:
max(f1-F1max)(f2-F2max)
(8)
式中:F1max和F2max分别表示发电费用和煤耗在约束条件下的最大值,可先由单目标优化分别求解得出。由Nash公理1可知,均衡点一定在多目标优化问题的帕累托前沿上取得。由于二次优化问题求解较为复杂,因此,可先求出原多目标优化问题的帕累托前沿,再从中搜索满足式(7)条件的解x0。选用SPEA2求解该双目标最优潮流问题的帕累托前沿。
2.3 基于SPEA2求解帕累托前沿
SPEA采用了协同进化规则的适应度分配策略和基于帕累托支配关系的小生境机制,与其他多目标演化算法相比具有更强的优化能力,而且需要设置的参数较少,是目前公认比较好的多目标问题优化方法,但存在适应度分配不精确以及多样性差等缺点[12]。针对上述缺点,SPEA2算法对SPEA算法进行了改进,成功地把精确的适应度分配策略、密度估计技术、增强截断方法结合在一起,收敛速度加快、帕累托最优解分布均匀。将发电机的有功功率和电压作为控制变量进行编码,不等式约束的处理采用罚函数的方式。SPEA2的算法流程如图1所示。
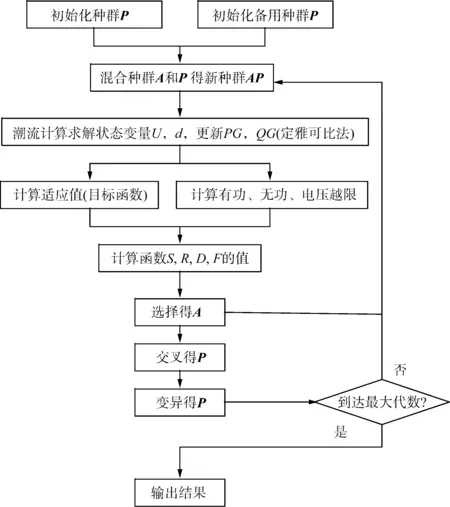
图1 SPEA2程序流程图Fig.1 Flow chart of SPEA2 program
步骤简介如下:
(1)初始化种群。采用随机生成一定数量个体的方式,初始化种群P和备用种群A,并混合种群A和P,得到新的种群AP。
(2)潮流计算。通过定雅克比矩阵法进行潮流计算,得到状态变量电压U和相角θ的值。
(3)计算适应值和罚函数。计算种群AP的适应值和罚函数。适应值即目标函数值f1和f2,罚函数值为违反约束的值,即查看有功、无功和电压越限情况。
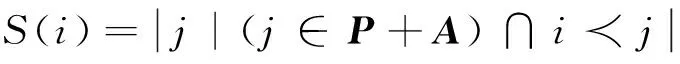
(5)计算函数值F。F=R+D,F的值越小越好。
(6)选择、交叉与变异。选择函数值F最小的前一半个体,生成新种群A。对新种群A进行模拟二项式交叉操作,进而生成新种群P。对新种群P进行高斯变异操作,再次生成新种群P。
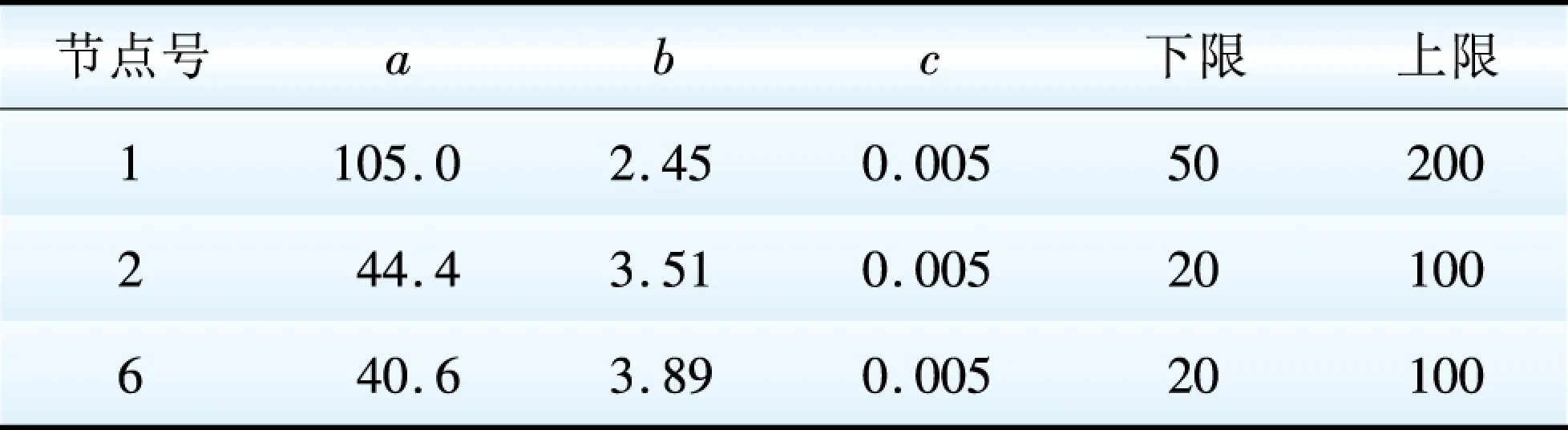
(7)终止条件。如果t 本文算例采用IEEE#14母线系统,功率基准值为100 MVA,母线电压上、下界分别为 1.1 和 0.95(标幺值),具体参数见文献[13]。发电机的经济参数见表1,其中下限、上限代表有功功率下限和上限,也就是在进行最优潮流计算时,有功源的上下限约束,此处为有名值。 根据2.3节中的SPEA2方法求解帕累托前沿,选取种群数量为50,最大遗传代数为200,算法以达到最大代数为终止条件。在此基础上,基于纳什讨价还价博弈寻优,找出最优点,最优解的结果在图2上标出,最终得出的结果是发电费用为28.345 5万元,网损是0.034 82 pu。相应的潮流计算结果如表2所示。 表1 算例发电机经济参数 Table 1 Economic parameters of generator in example 图2 基于遗传算法的帕累托前沿与讨价还价博弈的最优解Fig.2 Optimal solution based on GA’s Pareto front and Nash Bargaining Game 将转化成单目标优化问题后求得的最优解与基于演化计算和讨价还价博弈的多目标最优潮流计算比较,如表3所示。通过比较以式(9)和式(10)为目标函数的单目标算法,可看出将多目标最优潮流转化成单目标最优潮流问题时,不同的权重系数会带来不同的结果。采用式(9)的单目标函数进行计算时,可以获得较少的发电费用,但网损较大,而采用式(10)的单目标函数进行计算时,可以获得很少的网损,但发电费用较多。实际上发电费用与网损之间并没有明确的函数关系,因此单纯把二者加和所得的值进行最优化求解,本身物理含义不明确,且无法确定权重系数。但是讨价还价博弈算法则是在得到该双目标优化的帕累托前沿的基础上,进行讨价还价博弈,确定对博弈双方都最优的解,可以在获得较少的发电费用的同时,获取较小的网损,意义明确,结果可靠。因此,讨价还价博弈在求解该多目标最优潮流问题上具有优越性。 表2 潮流计算结果 Table 2 Power flow calculation results minf0=f1+f2 (9) minf0=f1/max(f1)+f2/max(f2) (10) 表3 最优解比较 Table 3 Comparison of optimal solutions 本文提出的基于演化计算和讨价还价博弈的多目标最优潮流算法,可以在考虑潮流平衡方程、有功上下限、无功上下限和电压上下限等约束的基础上,对模型的发电费用和网损进行优化。SPEA2算法可以获得较好的帕累托前沿,充分反映了2个目标函数之间相互影响又相互背离的关系,博弈方法进一步解决了这种不同目标函数之间的矛盾并得到最优解,具有明确的物理意义。通过算例表明了该算法的可行性与有效性。 [1]袁贵川,王建全,韩帧祥.电力市场下的最优潮流[J].电网技术, 2004,28(5):13-17. Yuan Guichuan, Wang Jianquan, Han Zhenxiang. Optimal power flow under electricity market[J].Power System Technology,2004,28(5):13-17. [2] 王彬, 何光宇, 卢建刚, 等. 考虑电网运行状态不确定性的最优潮流研究[J]. 电力建设, 2014,35(10): 1-6. Wang Bin, He Guangyu, Lu Jiangang, et al. Optimal Power Flow with Considering Operation State Uncertainty of Power System[J]. Electric Power Construction, 2014, 35(10): 1-6. [3] Wei H, Sasaki H, Kubokawa J. An interior point nonlinear programming for optimal power flow problems with a novel data structure[J]. IEEE Transactions on Power Systems, 1997, 13(3):870-877. [4] Yan Wei, Yu Juan, Yu D C, et al. A new optimal reactive power flow model in rectangular form and its solution by predictor corrector primal dual interior point method[J]. IEEE Transactions on Power Systems, 2006,21(1):61-67. [5] 刘明波,段晓军,赵艳. 多目标最优潮流问题的模糊建模及内点解法[J].电力系统自动化,1999,23(14):37-40. Liu Mingbo,Duan Xiaojun,Zhao Yan. Fuzzy modeling and interior point algorithm of multi-objective OPF problem[J]. Automation of Electric Power Systems,1999,23(14):37-40. [6] 卓峻峰,赵冬梅.基于混沌搜索的多目标模糊优化潮流算法[J].电网技术,2003,27(2):41-44. Zhuo Junfeng, Zhao Dongmei. A chaos optimization based algorithm for multi-objective fuzzy optimal power flow[J]. Power System Technology, 2003,27(2):41-44. [7] 唐忠, 蔡智慧, 黎文华. 基于免疫禁忌混合算法的多目标最优潮流计算[J]. 高电压技术, 2008, 34(9): 1954-1958. Tang Zhong, Cai Zhihui, Li Wenhua. Multi-objective optimal power flow calculation based on immune/Tabu search hybrid algorithm [J]. High Voltage Engineering, 2008, 34(9): 1954-1958. [8] 卫志农, 向育鹏, 孙国强, 等. 计及碳排放含有碳捕集电厂电网的多目标动态最优潮流[J]. 电网技术, 2012, 36(12): 11-17. Wei Zhinong, Xiang Yupeng, Sun Guoqiang, et al. Carbon emission-considered multi-objective dynamic optimal power flow of power system containing carbon-capture plant[J].Power System Technology,2012,36(12):11-17. [9] 叶承晋, 黄民翔. 考虑暂态稳定性的多目标最优潮流[J]. 中国电机工程学报, 2013, 33(10): 137-144. Ye Chengjin, Huang Minxiang. Multi-objective optimal power flow considering transient stability[J].Proceedings of the CSEE,2013, 33(10):137-144. [10] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. [11] Mendoza F, Bernal-Agustin J L, Dominguez-Navarro J A. NSGA and SPEA applied to multiobjective design of power distribution systems[J]. IEEE Transactions on Power Systems, 2006, 21(4): 1938-1945. [12] Zitzler E,Laumanns M,Thiele L. SPEA2: Improving the strength Pareto evolutionary algorithm[R], 2001. [13] 张伯明, 陈寿孙. 高等电力网络分析[M]. 北京:清华大学出版社,1996. (编辑:张媛媛) Multi-Objective Optimal Power Flow Based on Evolutionary Algorithm and Bargaining Game FU Yanlan1, ZHAO Xuelin2, LIU Kaicheng2, HE Guangyu3 (1. Hainan Power Grid Corporation, Haikou 570273, China;2. State Key Laboratory of Power Systems, Department of Electrical Engineering, Tsinghua University, Beijing 100084, China;3. Department of Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China) To solve the multi-objective optimal power flow (OPF) problem, genetic algorithm (GA) was used to find the Pareto front, and fully reflect the interaction and deviation internal relation of different optimal objective functions. On this basis, Nash Bargaining Game was used to get the global optimal solution. This paper discussed the multi-objective OPF problem with considering the minimum generation cost (or coal consumption) and the minimum system loss simultaneously. This paper firstly verified that the problem could satisfy the Nash Bargaining axiom, secondly obtained the Pareto front by strong Pareto evolution algorithm 2 (SPEA2), which could ensure faster convergence rate and more uniform Pareto front, and then used Nash Bargaining to find the optimal solution and solve the possible contradiction between the different objective function. Case study on IEEE 14-bus system verified the effectiveness of the proposed algorithm. multi-objective; optimal power flow (OPF); Nash Bargaining Game; genetic algorithm 国家高技术研究发展计划项目(863计划)(2012AA050201)。 TM 73 A 1000-7229(2015)05-0020-05 10.3969/j.issn.1000-7229.2015.05.004 2014-12-01 2015-02-04 付艳兰(1983),女,硕士,主要研究方向为电力系统自动化; 赵雪霖(1991),女,硕士研究生,主要研究方向为电器节能; 刘铠诚(1988),男,博士研究生,研究方向为无功电压自动控制、智能调度; 何光宇(1972),男,博士、教授、博士生导师,主要研究方向为智能调度与智能电网、优化技术及其在电力系统中的应用。 Project Supported by the National High Technology Research and Development of China (863 Program)(2012AA050201).3 算例分析
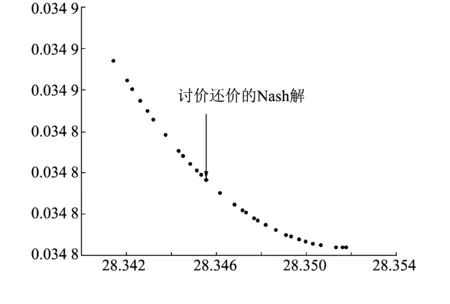
4 结 论

