基于子空间辨识和遗传算法的多回直流协调阻尼控制器设计

张中庆，张步涵，马怡晴，黄贻煜，马进霞，毛承雄

(1.中国电力工程顾问集团中南电力设计院，武汉市430071；2.强电磁工程与新技术国家重点实验室(华中科技大学)，武汉市430074)



基于子空间辨识和遗传算法的多回直流协调阻尼控制器设计

张中庆1，张步涵2，马怡晴1，黄贻煜1，马进霞1，毛承雄2

(1.中国电力工程顾问集团中南电力设计院，武汉市430071；2.强电磁工程与新技术国家重点实验室(华中科技大学)，武汉市430074)

提出了一种多回直流协调阻尼控制器的设计方法，用子空间辨识法对系统降阶建模，用遗传算法进行参数寻优，并对时滞系统稳定性进行了评估。首先利用基于Prony分析的主模比指标计算法选择直流控制器的广域输入信号，通过仿真得到扰动下系统输入输出数据，基于数据对系统进行子空间辨识，得到系统开环状态空间方程。其次将控制器加入开环系统得到闭环系统状态空间方程，以多种运行方式下的系统最小阻尼比最大化为优化目标，针对闭环系统状态空间方程，用遗传算法对控制器参数进行协调优化。采用基于自由权矩阵的时滞稳定性判据，分析含有多回直流协调控制器的广域电力系统的时滞稳定性。最后以南方电网为例，对多回直流协调阻尼控制器进行仿真，仿真结果表明，通过该方法所得到的多回直流协调阻尼控制器能够较好地提高电网阻尼水平，并满足时滞系统稳定性的要求。

子空间辨识；遗传算法；协调控制器；协调优化；时滞稳定

0 引 言

随着我国电力系统的发展及“西电东送、南北互供、全国联网”战略的实施，我国大区电网之间的互联已经进入了规划和实施阶段，电力系统逐渐呈现出大区电网互联，远距离、大容量送电，多回交、直流并联运行等特点和发展趋势。然而随着交、直流混合电网的发展，电网动态稳定问题日益复杂，区间弱阻尼问题成为大规模交、直流混合电网面临的主要挑战之一[1-2]。由于多回大容量特高压直流输电系统，具有响应速度快、可控程度高、调节容量大、横跨区域广等特性，为改善系统的动态性能提供了有力的手段，其中直流附加阻尼控制作为直流调制控制的有效方式得到了广泛研究[3]。为抑制区域电网互联低频振荡，国内目前已建成的直流输电系统均带有双侧频差调制功能(power swing damping/power swing stabilization, PSD/PSS)，但在历次振荡事件中，自带的调制功能并未发挥理想的作用。

目前直流协调阻尼控制器设计主要包括结构设计、参数适配、仿真校验等设计环节。本文将系统状态空间辨识、遗传算法应用于控制器的设计中，重点从控制器的结构和参数方面解决多回直流协调阻尼控制问题。

1 广域反馈信号选择

对于大规模电力系统，广域监测系统(wide area measurement system，WAMS)能为广域直流协调阻尼控制器提供大量备选的反馈输入信号。但是，从控制难度和经济的角度考虑，不可能将全部的广域反馈信号都用于控制器的输入，一般选择对区间模式可观度最强的一个或几个信号，因此，反馈信号的选择是广域直流协调阻尼控制器设计的关键所在。可供选择的广域信号很多，包括传输线上的有功潮流、远方发电机母线功角、发电机转差等[4]。由于主模比指标法可比较不同类型反馈信号的可观性，其反映了信号中指定模式的相对强度，可以用来量化地比较来自不同测点的广域信号对指定模式可观性的大小[7]。因此，本文采用基于Prony分析的主模比指标计算法进行广域反馈信号的选取。根据输出反馈控制的一般要求，选取可观性好，即主模比大的信号作为广域反馈信号。

Prony辨识方法的信号模型[5]为

(1)

式中：y(k)为信号离散化的取值；k为离散的时间变量；Ai、θi、ai、fi分别为对应第i个模式的振幅、初相位、衰减因子、频率;p为模型的阶数;Δt为时间间隔。

则主模比指标可表示为

(2)

2 基于子空间辨识的系统闭环方程

2.1 子空间辨识原理

线性时不变系统的状态空间模型[6-7]可表示为

(3)

式中：xk为状态变量；uk为系统输入；yk为系统输出；A、B、C、D为相应的系数矩阵,对于m输入l输出的n阶系统，A∈Rnm,B∈Rnm,C∈Rln和D∈Rlm。

对由上式所表示的系统定义符号：

(1)输入输出Hankel矩阵

(4)

(5)

式中：Uo|i-1为输入Hankel矩阵；Yo|i-1为输出Hankel矩阵。

(2)广义可观测矩阵Γi

Γi=(CCACA2…CAi-1)T

(6)

(3)下三角Toeplitz矩阵Hi

(7)

(4)状态矩阵

X=(xi,xi+1,xi+2,…,xk+j-1)

(8)

则可推出

(9)

其中

(10)

(11)

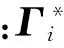
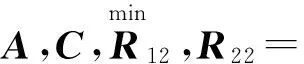
(12)

2.2 闭环系统状态空间方程

闭环控制系统为输出量直接或间接反馈到输入端，形成闭环参与控制的系统，对于多输入多输出开环系统，为提高系统稳定性，加入直流附加阻尼控制器作为反馈，附加阻尼控制器结构如图1所示。

图1 附加阻尼控制器结构Fig.1 Additional damping controller structure

由于多输入多输出系统辨识为状态空间形式，因此要将控制器加入系统，必须先将控制器由传递函数形式,即公式(13)，转换到状态空间形式，即公式(14)，由自动控制原理传递函数转换到状态空间的推导理论可得到控制器状态空间方程的Ac、Bc、Cc、Dc矩阵分别如式(15)～(18)所示。

(13)

式中：Y(s)为控制器输出信号；U(s)为控制器输入信号；K为控制器放大增益；T1、T2、T3、T4为控制器移相环节参数；s为拉普拉斯变换复变量。

(14)

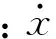
(15)

(16)

Cc=[0 1]

(17)

(18)

对于如图2所示的多输入多输出闭环系统，状态空间方程推导过程如式(19)～(22)所示。

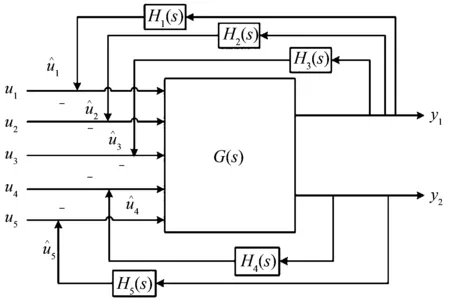
图2 多输入多输出闭环系统Fig.2 Multiple input and multiple output closed-loop system

单回直流附加阻尼控制器状态空间方程由公式(14)给出，5回直流附加阻尼控制器的状态空间方程由公式(19)给出。

(19)

基于系统开环状态空间方程的辨识结果：

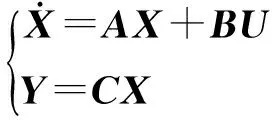
(20)

系统闭环状态空间方程矩阵为

(21)

(22)

3 遗传算法寻优

3.1 遗传算法原理

遗传算法是模仿自然界生物进化而发展起来的随机全局搜索和优化方法，其借鉴了达尔文的进化论和孟德尔的遗传学说[8-10]。遗传算法，本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并且可以自适应地控制搜索过程以求得最优解。遗传算法对优化问题本身没有太多限制，因此适用范围广，并且在优化单元数量较多时，遗传算法具有较高的寻优效率。

遗传算法的基本步骤包括：编码、初始种群的形成、适应度值评价、选择、交叉、变异、终止条件判断。

3.2 问题模型

在小干扰稳定分析中，阻尼比是衡量系统动态性能的指标，阻尼比越大，系统的动态性能越好，因此将获得较大的阻尼比作为控制器参数优化的目标。由于存在多种低频振荡模式，控制器参数变化在提高一种振荡模式阻尼比的同时可能降低另一种振荡模式的阻尼比，因此要考虑在多种振荡模式下的控制器参数协调优化。

控制器参数为K、T1、T2、T3、T4，根据控制器参数设计有关理论和经验，T2、T4为给定值，均取0.1，K、T1、T3为待优化量。

(23)

约束条件

(24)

目标函数

(25)

式中：ξj为第j个振荡模式的阻尼比，即目标函数为多振荡模式下最小阻尼比的最大化。

算法流程如图3所示。

4 时滞系统稳定性分析

4.1 考虑时滞的广域电力系统建模

对于大规模的电力系统，其线性模型的阶数一般都很高，这使得时滞稳定裕度计算很困难甚至不可行，因此，可以在子空间辨识方法得到的降阶模型的基础上进行时滞稳定性分析。将系统状态方程的某一稳定运行点，线性化后可得如下状态空间模型：

(26)

式中：x1(t)为模型的状态变量；A1、B1、C1分别为电力系统的状态矩阵；u(t)、y(t)分别为输入矩阵和输出矩阵。

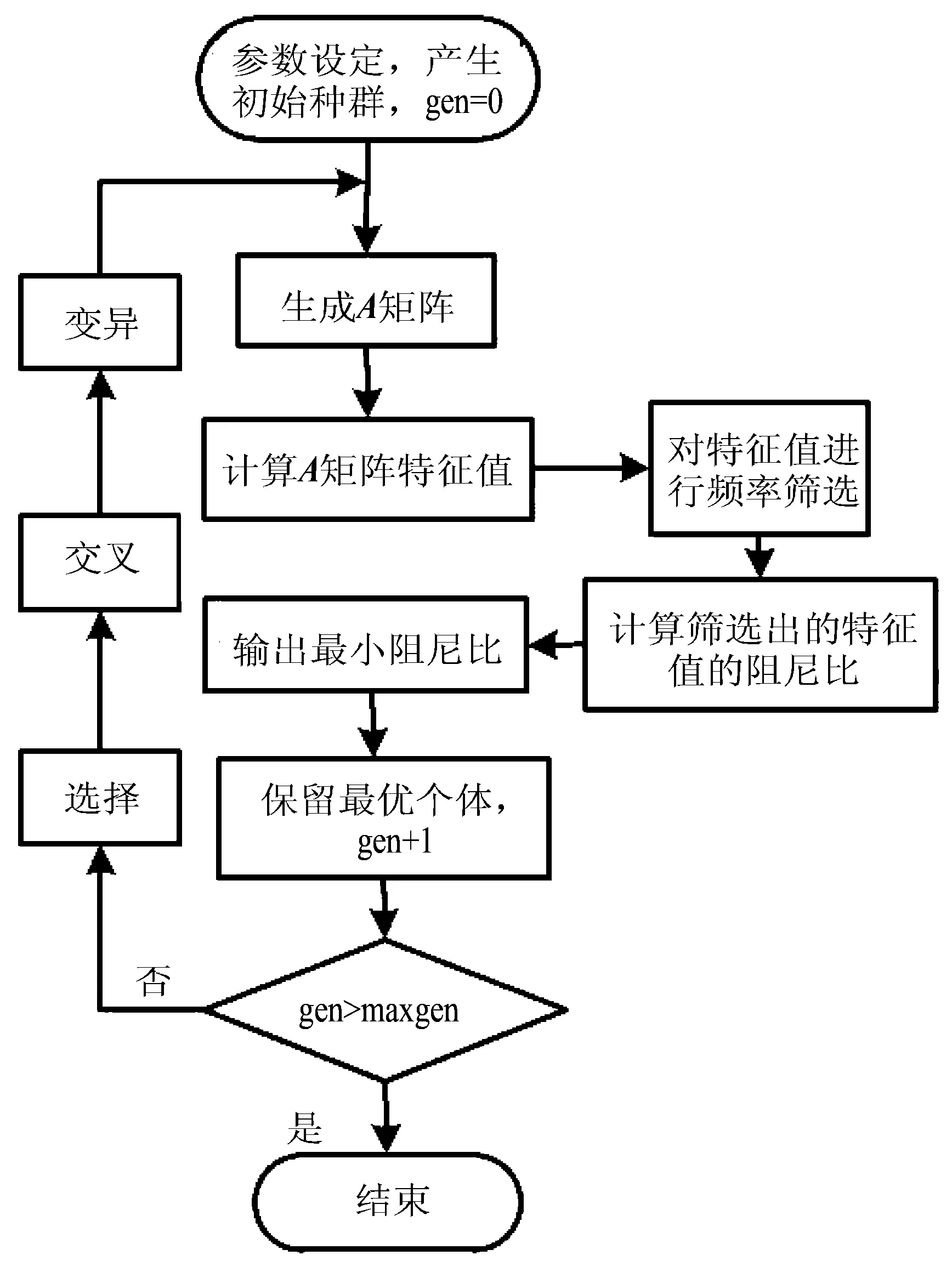
图3 算法流程Fig.3 Algorithm process

直流协调阻尼控制器的状态空间方程可表示为

(27)

式中：x2(t)、y2(t)、u2(t)分别为广域直流附加阻尼控制器的状态变量、输出变量和输入变量；A2、B2、C2分别为广域直流控制器的状态矩阵、输入矩阵和输出矩阵。

设广域信号的时滞为τ，则

(28)

含降阶广域系统、广域直流控制器和时滞的闭环电力系统可以表述为以下模型[11]:

(29)

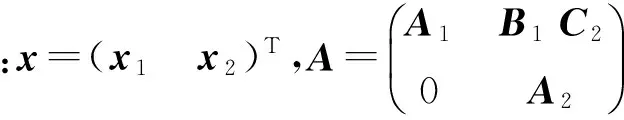
4.2 时滞系统稳定性判别

对于时滞系统，设τ为时滞，τd为时滞稳定裕度，当τ<τd时，时滞依赖系统保持渐进稳定，当τ>τd时，时滞依赖系统不稳定。τd是判断时滞依赖系统稳定性的判据。

时域仿真法、Smith补偿法、基于Lyapunov直接分析法等均可以用来计算时滞稳定裕度τd，但是这些方法的计算结果都不同程度地偏于保守，本文结合基于自由权矩阵的单时滞系统和多时滞系统的时滞稳定性判据，利用线性矩阵不等式，计算相应时滞稳定裕度。

采用自由权矩阵方法来分析含有广域直流附加阻尼控制器的电力系统的时滞稳定性及求解时滞系统的时滞稳定裕度，主要思想及步骤如下：

(1)利用子空间辨识方法，建立含时滞的闭环电力系统模型。将广域直流附加阻尼控制器的方程写成状态空间形式，并引入广域信号时滞，然后得到时滞系统闭环模型。

(2)开发基于自由权矩阵的时滞稳定性分析程序。结合基于自由权矩阵的单时滞系统和多时滞系统的稳定性判据，利用线性矩阵不等式处理方法，进行时滞系统稳定性判定及稳定裕度计算程序开发。

(3)时滞上限的计算。根据系统闭环电力系统模型，结合基于自由权矩阵的时滞系统稳定性判据，在给定时滞情况下判定时滞系统的稳定性，多次试算得到时滞稳定上限值。

5 算例分析

本文以南方电网2015年“丰大”运行方式及其检修方式为例，进行小干扰稳定分析、系统状态空间的子空间辨识及多回附加阻尼控制器参数的协调优化等研究。

基于BPA软件对2015年“丰大”方式下南方区域电网进行小干扰稳定计算，结果显示存在3个区域间振荡模式：(1)云南对广东的振荡模式，振荡频率为0.360 5Hz，阻尼比为0.096 3；(2)云南、广东对贵州的振荡模式，振荡频率为0.498 6Hz，阻尼比为0.058 6；(3)海南对主网的振荡模式，振荡频率为0.817 5Hz，阻尼比为0.056 4。由于南方电网直流线路联络了云南、贵州、广东区域，而海南与主网之间无直流联系，因此调制直流功率对海南-主网模式的阻尼影响不大，因此本文仅针对云-广模式、云广-贵模式进行研究。

根据主模比指标可筛选出可观性较好的信号作为控制器反馈信号：云-广模式选择1/3(f罗平+f普洱+f昭通-f从化-f罗洞-f宝安)频率差信号，云广-贵模式选择1/3(2f高坡+f兴仁-f从化-f楚雄-f罗平)频率差信号。

系统多输入为矩阵波激励信号，分别为溪洛渡直流ΔP1、糯扎渡直流ΔP2、楚穗直流ΔP3，高肇直流ΔP4、兴安直流ΔP5，激励信号如图4所示，幅值为0.25倍额定功率，持续1 s。

多输入多输出系统状态方程中矩阵A反映系统的稳定性，对辨识出的矩阵A进行特征值分析，可得到系统的低频振荡相关信息，如表1所示。2015年“丰大”运行方式下云广-贵模式的低频振荡频率为0.498 6 Hz、云广模式的低频振荡频率为0.360 5 Hz，辨识结果的误差分别为9.2%、5.1%，误差均小于10%，因此子空间辨识得到的状态空间方程能较好地反映5输入2输出系统的低频振荡特性。

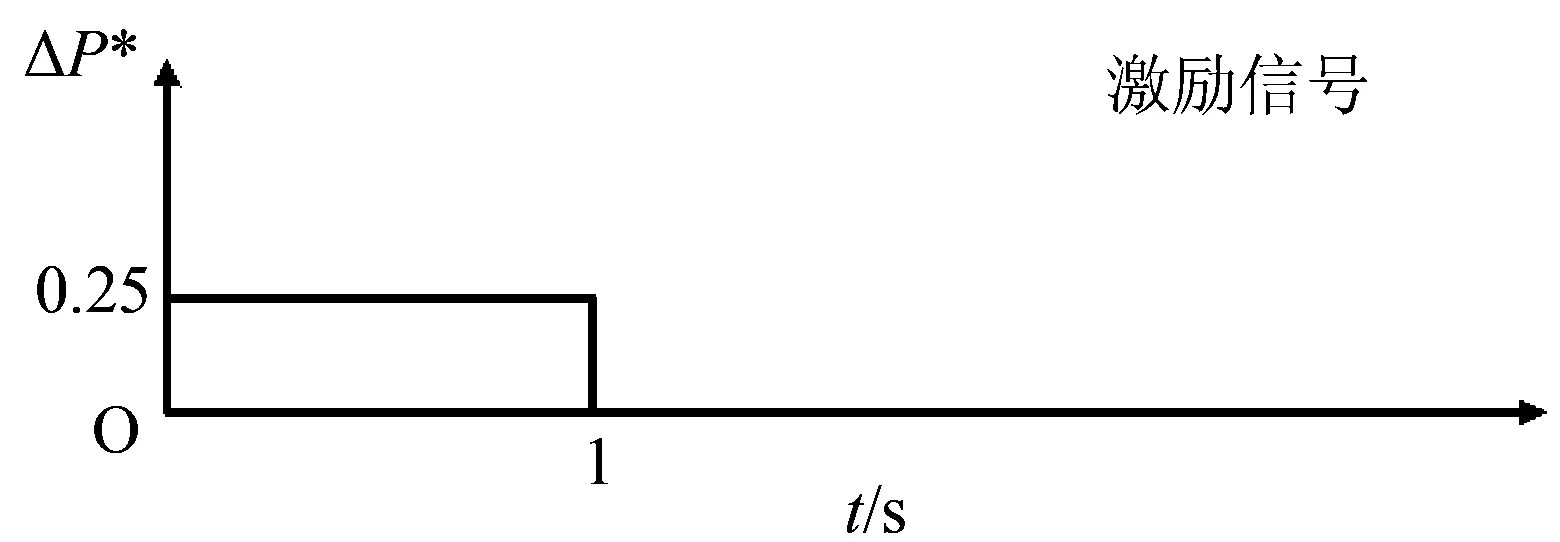
图4 激励信号Fig.4 Excitation signal

表1 矩阵A的特征值分析结果

Table 1Amatrix eigenvalue analysis results

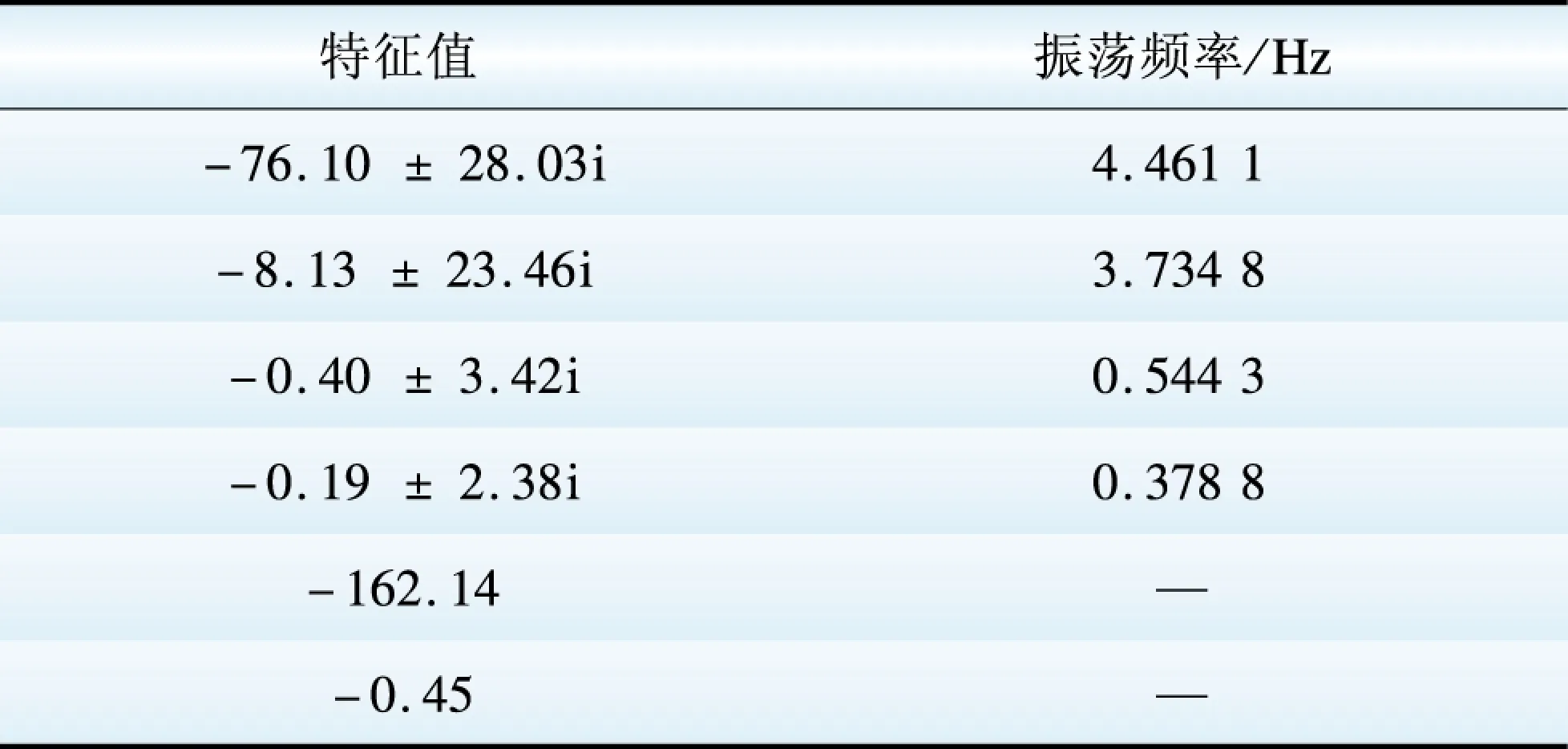
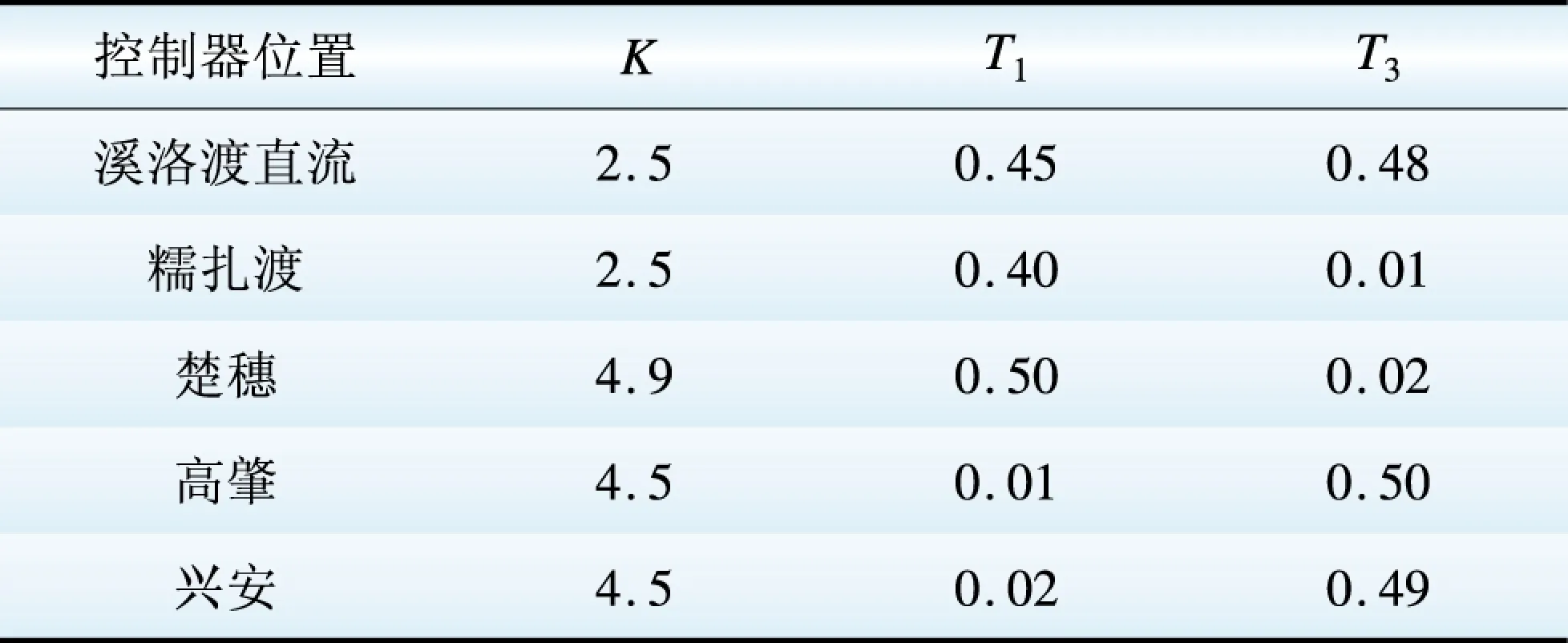
表2 控制器参数优化结果表

Table 2 Optimization results of controller parameters

为了分析多回直流协调阻尼控制器对系统动态稳定特性的影响效果，以南方电网“西电东送”通道贤令山—花都500 kV交流线路三相短路跳单回线路故障(N-1故障)作为扰动故障，重点考查扰动后云南交流出口通道罗平—百色500 kV线路、贵州交流出口通道黎平—桂林500 kV线路功率振荡情况如图5、6所示。仿真表明，投入控制器后，山花线N-1故障后，罗百线、黎桂线功率振荡幅度较小，振荡平息的时间也较短。可见，多回直流协调阻尼控制器能够有效改善系统动态稳定特性，提高扰动故障后系统的阻尼。

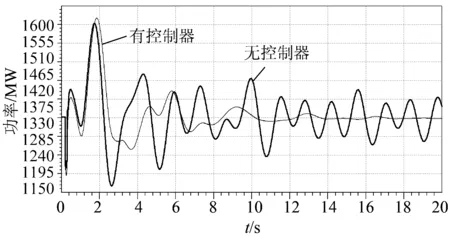
图5 罗百线仿真功率曲线Fig.5 Simulated power curve of Luobaixian

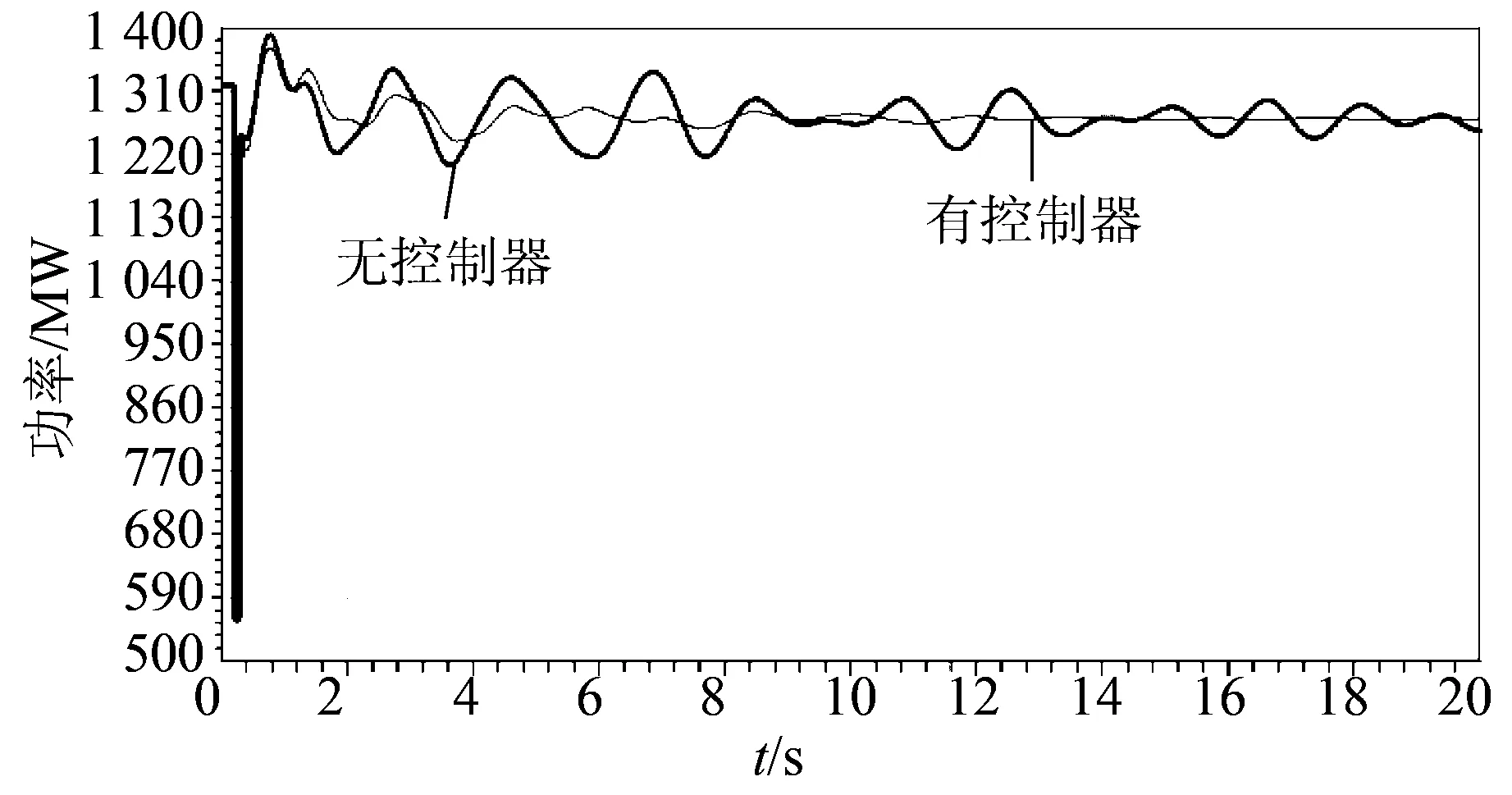
图6 黎桂线仿真功率曲线Fig.6 Simulated power curve of Liguixian

通过基于自由权矩阵的多时滞稳定裕度计算程序分析可知，基于所考虑的南方电网多典型方式，系统总时滞稳定裕度为233 ms。由于南方电网直流协调控制系统在系统时滞约80 ms，因此系统在多种典型运行方式下均能保持时滞稳定。

6 结 语

致 谢

本研究得到了中国顾问集团公司、南京南瑞继保有限公司的大力支持，特此表示感谢！

[1]朱方，赵红光，刘增煌，等.大区电网互联对电力系统动态稳定性的影响[J].中国电机工程学报，2007，27(1)：1-7. Zhu Fang, Zhao Hongguang, Liu Zenghuang, et al. The influence of large power grid interconnected on power system dynamic stability[J]. Proceedings of the CSEE, 2007,27(1):1-7.

[2]孙景强，陈志刚，曹华珍，等.南方电网2010年低频振荡问题[J].电网技术，2007，31(2)：93-97. Sun Jingqiang, Chen Zhigang, Cao Huazhen, et al. Analysis on low-frequency oscillation of South China power grid in 2010[J]. Power System Technology, 2007, 31(2):93-97.

[3]Kundur P. Power system stability and control[M]. New York, USA: McGraw-Hill Inc, 1994.

[4]亓玉丽.多馈入直流系统调制控制的广域最优协调设计[D].北京：华北电力大学,2006. Qi Yuli. Design on wide-area coordination and optimization in multi-infeed HVDC transmission system modulations control[D].Beijing: North China Electric Power University, 2006.

[5]韩民晓，文俊，徐永海，等.高压直流输电原理与运行[M].北京：机械工业出版社，2010.

[6]王锡凡，方万良，杜正春.现代电力系统分析[M].北京：科学出版社，2003.

[7]张贤达.现代信号处理[M].北京：清华大学出版社，2002.

[8]雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2005.

[9]Abido MA.Parameter Optimization of Multimachine Power System Stabilizers Using Genetic Local Search[J].Electrical Power and Energy System，2001,23(8):785-794.

[10]牛振勇，杜正春，方万良，等.基于进化策略的多机系统PSS参数协调优化[J].中国电机工程学报，2004,24(2):22-27. NiuZhenyong, Du Zhengchun, Fang Wanliang, et al. Parameter optimization of multi-machine power system stabilizers using evolutionary strategy[J].Proceedings of the CSEE, 2004, 24(2):22-27.

[11]姚伟,文劲宇,程时杰,等. 考虑时滞影响的SVC广域附加阻尼控制器设计[J]. 电工技术学报,2012,27(3):239-246. Yao, Wei, Wen Jinyu, Cheng Shijie, et al. Design of wide-area supplementary damping controller of SVC considering time delays[J]. Transactions of China Electrotechnical Society, 2012, 27(3):239-246.

(编辑：张小飞)

Multiple-Loop HVDC Coordination Damping Controller Based on Subspace Identification and Genetic Algorithm

ZHANG Zhongqing1, ZHANG Buhan2, MA Yiqing1,HUANG Yiyu1, MA Jingxia1, MAO Chengxiong2

(1. Central Southern China Electric Power Design Institute of CPECC, Wuhan 430071, China;2. State Key Laboratory of Advanced Electromagnetic Engineering and Technology,Huazhong University of Science and Technology, Wuhan 430074, China)

A design method was proposed for multi-loop DC coordination damping controller, which used subspace identification to reduced order modeling for system, used genetic algorithm for parameter optimization, and estimated the stability of time-delayed system. Firstly, the wide-area input signal of DC controller was selected by using dominate mode ratio index calculation method based on Prony analysis; the input and output data of the system under disturbance were obtained according to the simulation; and the open-loop state space equation was obtained by system subspace identification based on the data. Secondly, adding the controller in the open-loop system to get closed-loop system state space equation. Moreover, with maximizing the minimum damping ratio of the system under various operation modes as the optimization goal, genetic algorithm was used to coordinately optimize the controller parameter in closed-loop system state space equation. The stability criterion of system with time-delay based on free-weighting matrices was used to analyze the stability of system with time-delay for wide-area power system with multi-loop DC coordination controller. Finally, taking China Southern Power Grid as an example, the multi-loop DC coordination damping controller was simulated. The simulation results show that the multi-loop DC coordination damping controller obtained by this method can better improve the damping level of power gird, and meet the requirements of the stability of time-delayed system.

subspace identification; genetic algorithm; coordination controller; coordination optimization; stability of time-delayed system

中国电力工程顾问集团公司科技项目(DG1-R02-2012)。

TM 712

A

1000-7229(2015)05-0060-06

10.3969/j.issn.1000-7229.2015.05.010

2015-01-05

2015-03-18

张中庆(1982)，男，硕士，工程师，主要从事安全稳定控制系统、直流控制保护方面的研究；

张步涵(1950)，男，硕士，教授，主要从事电力系统分析与规划方面的研究；

马怡晴(1975)，女，本科，高级工程师，主要从事安全稳定控制系统、直流控制保护、电力调度自动化方面的研究；

黄贻煜(1979)，男，硕士，高级工程师，主要从事安全稳定控制系统、直流控制保护、电力调度自动化方面的研究；

马进霞(1957)，女，本科，教授级高级工程师，主要从事安全稳定控制系统、直流控制保护、电力调度自动化方面的研究；

毛承雄(1964)，男，博士，教授，主要从事电力系统运行与控制、大功率电力电子技术在电力系统的应用等方面的研究。