基于控制变量法的一维光子晶体态密度特性的研究

胡迎宾， 廖同庆， 吴 昇， 魏小龙

（1.安徽大学 电子信息工程学院，安徽 合肥 230601；2.合肥师范学院 计算机学院，安徽 合肥 230601）

光子晶体是一种介电常数周期性变化的人工微结构材料，其具有特殊禁带和导带［1－2］，在禁带处，相应频率的光子不能通过光子晶体，导带处则可以通过。光子的这种行为类似于半导体能带结构所形成的禁带和导带中电子的行为。为了方便讨论一维光子晶体的禁带特性，引出了态密度（density of states，DOS）这一物理参考量，其表示的含义是光子在电磁特性下，单位体积内特定频率附近单位宽度上的光子电磁本征态的数量，间接反映了光子在光子晶体中的传播特性［3－5］。

根据Fermi’s golden rule在原子微腔内自发辐射几率正比于DOS，因此可通过调制DOS的分布，改变电偶极子辐射几率，如金属腔、介质腔、超晶格等，通过增强自发辐射制成光子带边激光器［6］。本文研究一维周期性光子晶体的DOS特性，以便控制光子在光子晶体中的传播。

1 一维光子晶体DOS的计算

当单位振幅光波穿过一层薄膜，由薄膜光学理论可知，薄膜两侧相位差δ1＝（2πn1dcos C1）／λ，C1为透射角（C1＝arcsin［（n0sin C0）／n1］，C0为入射 角 ），再 引 入 参 数cos2C1＝，则薄膜的传输矩阵M1［7］为：

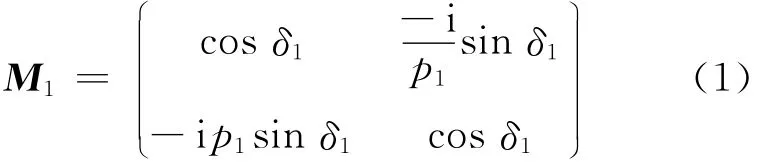
同理，进一步可以得到第2层的传输矩阵M2。

N周期一维光子晶体介质参数分布示意图如图1所示，一维光子晶体由2层薄膜周期性组成，薄膜的传输矩阵分别为M1和M2，则N周期的光子晶体的传输矩阵MN为：

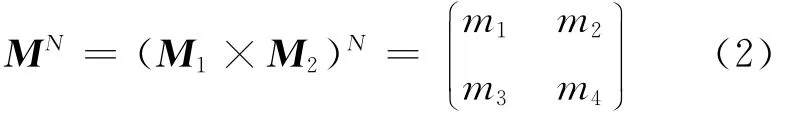
同理可得一维N周期的光子晶体的反射率rN和透射率tN为：

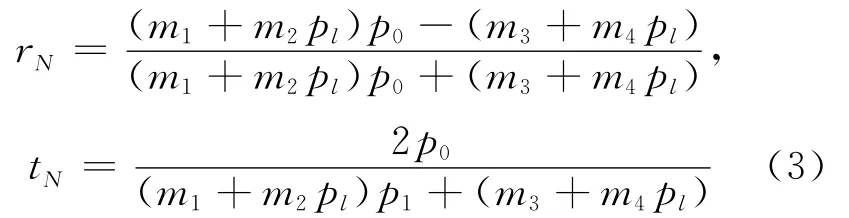
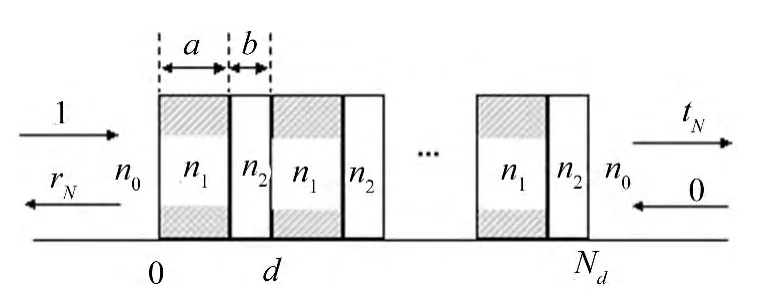
图1 N周期一维光子晶体介质参数分布示意图

通过引入无限多个单个周期单元组成介质材料的Bloch函数uB和Bloch位相β，可得到单个周期的（N＝1）透射系数t倒数的实部与Bloch位相β的关系［8］，即

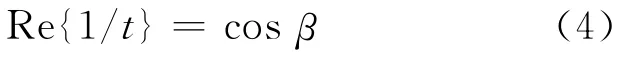
用X、Y分别表示t的实部和虚部，XN、YN表示tN的实部和虚部，可得：

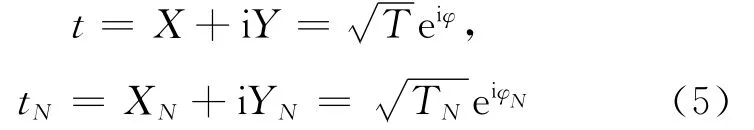
令T＝X2＋Y2，ξ＝X／T，η＝Y／T，则有：

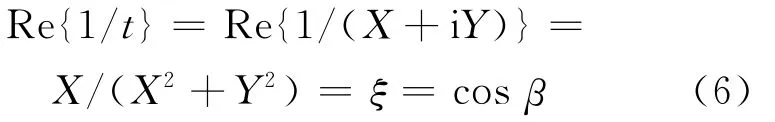
一维N周期光子晶体的DOS［8］为：

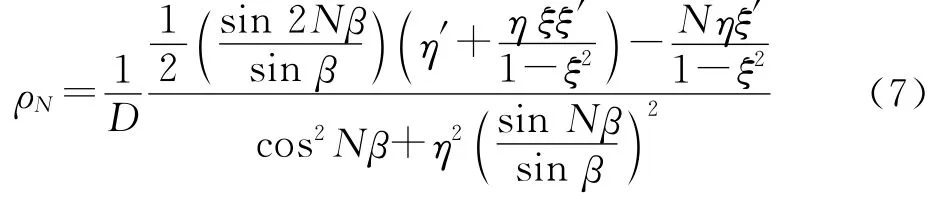
其中，D＝Nd为N个周期一维光子晶体的总长度；ξ′和η′均表示对ω微分。

由上述公式推导可知，当2种材料周期性构成的一维光子晶体，周期数N一定时，影响态密度变化的变量是入射光的频率ω，而λ＝2πc／ω，将ω用λ代入，可知ρN是关于波长λ的函数，从而可以绘制出DOS随波长λ变化的波形。

2 一维光子晶体DOS特性

假设一维光子晶体是由折射率分别为n1和n2的2种薄膜材料周期性构成，中心波长为λ0＝600nm，薄膜厚度满足：其中，ω0为中心波长下对应的频率。

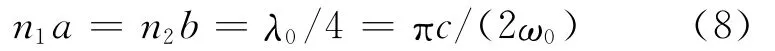
利用上述公式可以推导计算出透射率t的实部和虚部，从而计算出ξ和η及其导数的值，并代入（7）式计算出DOS随波长λ的变化关系。

2.1 不同折射率比下光子晶体的DOS

分别选取4组折射率比值不同的薄膜构成的一维周期性光子晶体，4组材料见表1所列，周期数N＝20，其DOS曲线如图2所示。

表1 4组光子晶体的组成材料

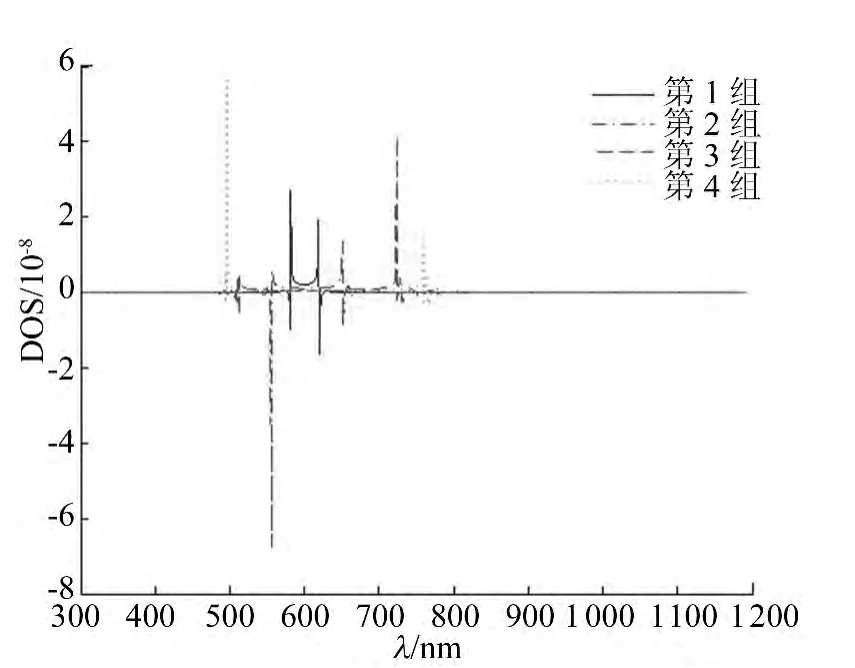
图2 不同折射率比下光子晶体的DOS曲线

由图2可见，DOS受到光子晶体周期性结构的调制作用，出现了极强的波动性，可以看出通过调制DOS，也就控制了光子在光子晶体中的传播。DOS波形明显地显示出了光子晶体所形成特有的禁带特性，如4组DOS曲线在中心波长λ＝600nm附近，DOS接近于0，即此处的光子电磁本征态的数量接近于0。对比4组曲线，观察到禁带的宽度随着选取的薄膜材料折射率比值的增大而增大；在禁带和导带边缘位置会出现突然增强的现象，这是光子晶体的一个重要特性。

2.2 不同周期数下光子晶体的DOS

讨论周期数对DOS的影响，假定选取的2种薄膜材料是由上面的第2组构成，其他条件设定和上面相同，则可以绘制出周期数分别在5、10、20、50情况下的DOS曲线，如图3所示。

由图3可知，中心波长λ＝600nm附近存在光子晶体的禁带。但在图3中，不同周期数下的禁带宽度相同，即周期数的改变并不影响禁带的带宽，而是增强了光子晶体对入射光的调制作用，随着周期数的增加，态密度曲线波动性增强，且在禁带边缘处DOS突然增强的现象更加明显。作为文献［2］的对比验证，一维周期性光子晶体的禁带宽度与构成的材料的折射率比有关，与光子晶体的周期数无关，这一结论与文献［2］完全相同。

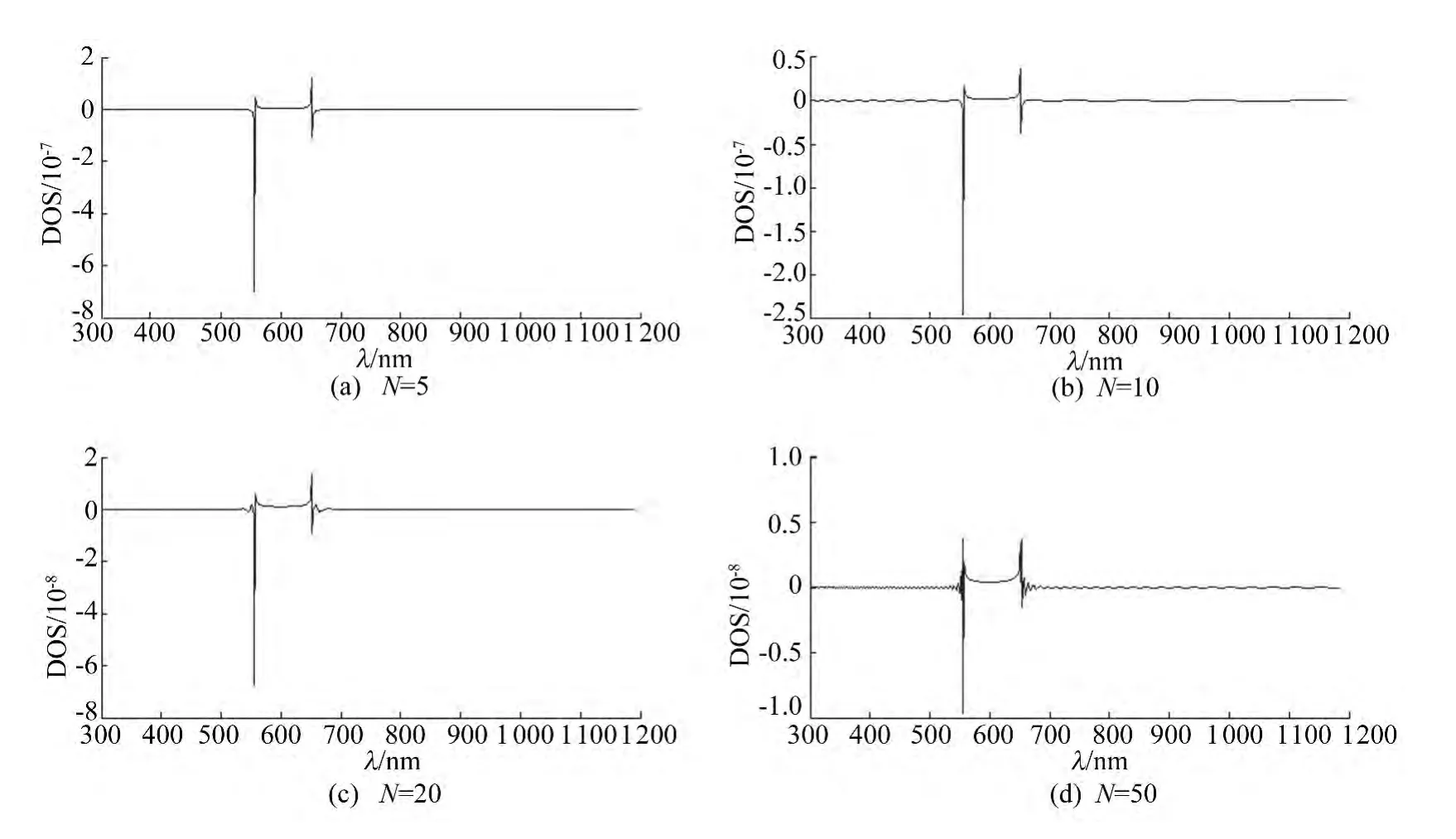
图3 不同周期数下光子晶体的DOS曲线

3 禁带边缘处DOS增强

为了方便讨论波长λ对β的影响，选择第2组材料构成一维光子晶体，周期数N＝20，在相应条件下，定义一个群速度v为：

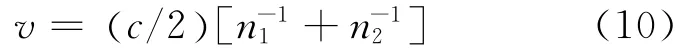
对于确定的薄膜材料构成的光子晶体，v是一个常量，用ρNv表示归一化的DOS，绘制Bloch位相β以及相同条件下归一化的DOS随波长变化的曲线，如图4所示，相同条件下的β′的曲线如图5所示。

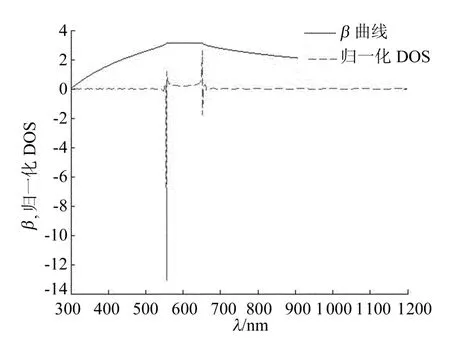
图4 β和归一化DOS随入射光波长的变化曲线

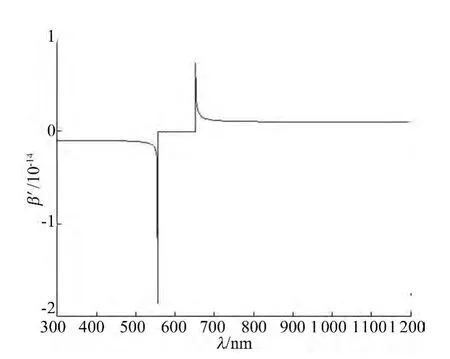
图5 β′随入射光波长的变化情况

由（7）式可知，当Nβ＝mπ（m＝0，1，2，…，N－1）时，sinNβ＝0、sin 2Nβ＝0、cos2Nβ＝1，此时ρN分母快速变化项的值为1，为极小值，其分子的值为Nηξ′／（1－ξ2）。即当β从0变化到π时，ρN有N个局域的最大值，即

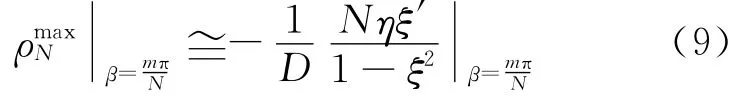
由此可知，当入射光波长改变时，β也随之改变，从而导致ρN的变化。观察图4、图5中光子晶体禁带位置，β值的大小保持不变，而在非禁带处，其值处于持续的变化状态；在禁带边缘处，β的变化率出现了极强的突变现象，由此可推导出光子禁带边缘处的突然增强现象，与β的变化率有着很大的关系。

4 结束语

本文通过数值计算分析了一维周期性光子晶体的DOS，并基于控制变量法，计算出不同折射率比值、不同周期数的一维周期性光子晶体DOS随入射光波长λ的变化特性；研究了DOS随入射光波长变化时，光子禁带边缘处的突然增强现象。分析表明边缘处增强的现象与Bloch位相β的相应变化有关。

［1］ Wang R L，Zhang J，Hu Q F.Simulation of band gap structures of 1Dphotonic crystal［J］.Journal of the Korean Physical Society，2008，52：S71－S74.

［2］ 黄弼勤，顾培夫.一维光子晶体禁带的展宽［J］.光学学报，2003，23（12）：1497－1501.

［3］ Rudzinski A，Zawadzka A T，Szczepanski P.Simple model of the density of states in 1Dphotonic crystal［C］／／Photonic Crystals and Fibers：Proc SPIE 5950，2005：59501A1－59501A8.

［4］ 陈慰宗，郑新亮，付灵丽，等.一维光子晶体中的电磁模密度［J］.光子学报，2003，32（2）：239－243.

［5］ Wang Hong，Fang Yuntuan.Achieving transparent photonic band in regular one－dimensional photonic crystal［J］.Journal of Infrared，Millimeter，and Terahertz Waves，2011，32（1）：47－54.

［6］ Deppe D G，Huang H.Fermi’s golden rule，nonequilibrium electron capture from the wetting layer，and the modulation response in P－doped quantum－dot lasers［J］.IEEE J Quantum Electron，2006，42（3）：324－330.

［7］ 王 辉，李永平.用用特征矩阵法计算光子晶体的带隙结构［J］.物理学报，2001，50（11）：2172－2178.

［8］ Bendickson J M，Dowling J P，Scalora M.Analytic expressions for the electromagnetic mode density in finite，one－dimensional，photonic band－gap structures［J］.Phys Rev E，1996，53（4）：4107－4121.