一种无证书的顺序聚合签名方案
汤小超, 王 斌, 杨 睛, 李 纯
(扬州大学 信息工程学院,江苏 扬州 225127)
近年来人们对数字签名的变体进行了多方面的研究[1-2]。聚合签名方案[2]将来自不同的n 个用户的对n个消息的n个不同的签名进行聚合,从而生成一个聚合签名。聚合签名可以简化信息验证的过程,从而减少验证签名需要的计算量和数据存储。聚合签名分为无序的聚合签名[2]和顺序的聚合签名[3]2种。
由于基于身份的公钥密码系统[4]存在固有的密钥托管问题,文献[5]提出了无证书的公钥密码系统,该系统的私钥由用户和密钥生成中心(key generate center,KGC)共同生成,所以无证书的公钥密码系统解决了密钥托管的问题,以该方案为基础,研究者提出了许多无证书的签名方案。文献[6]提出了基于双线性映射的2个无证书聚合签名方案。文献[7]利用双线性映射构造方案,提高了签名以及验证过程中计算效率。文献[8]提出在消息签名阶段不需要双线性映射的计算,而且在验证阶段也只需要2步的双线性映射的计算,所以该方案在签名验证时更加高效。
文献[9]的方案是在无证书签名方案的基础上提出的,并给出了正式的安全模型,本文将该方案[9]的部分密钥提取部分与自认证体制[10]相结合,保证了密钥分配中心生成部分密钥在信道传输时的安全性,并对文献[9]方案的签名、聚合签名及聚合验证部分进行了改进,提出了一种无证书的顺序聚合签名方案,并进行了安全性分析。性能分析表明,新提出的顺序聚合签名方案可以改善聚合签名的效率。
1 无证书的顺序聚合签名方案
无证书的顺序聚合签名方案是在文献[9]方案的基础上进行扩展得到的,该方案包含以下算法。
1.1 系统设置
KGC选取一个安全参数k。选取一个循环群G1,G1的生成元为P,其阶为素数p。一个循环群G2,其阶也为素数p。双线性映射e:G1×G1→G2。除此之外,KGC再选取一个随机数λ∈作为系统主密钥,计算PT=λ·P。选取3个Hash函数如下:
H1:{0,1}*→G1,
H2:{0,1}*→G1,
H3:{0,1}*→G1。
所以系统的参数列表为:
params= 〈G1,G2,e,P,PT,H1,H2,H3〉。
消息空间为:
M = {0,1}*。
其中,PT为系统公钥。
1.2 生成用户密钥
一个用户 Ui,其身份为IDi={0,1}* ,Ui随机选取一个数作为用户私钥,计算Xi=xi·P,Yi=xi·PT,Pi=(Xi,Yi)作为用户公钥。
1.3 生成部分私钥
用户Ui将自己的身份IDi和自己的公钥Pi传送给KGC,接着KGC计算出Di=λ·Qi,其中Qi=H1(IDi,Pi),并将Di作为部分私钥。KGC随机选取一个数,计算Ai=ai·P,Bi=Di+ai·Xi,最后 KGC通过公共的通道将(Ai,Bi)发送给相应的用户Ui。
用户Ui收到KGC发送的(Ai,Bi)信息后,计算Di=Bi-xi·Ai,用户Ui就可得到部分私钥Di。用户将Di和xi作为签名密钥。
1.4 签名
用户U1的身份为ID1,选取消息m1∈M 和签名密钥D1、x1,P1=(X1,Y1)作为用户公钥。具体签名步骤如下:
(1)选取一个随机数r1∈Z*p,并计算R1=r1·P。
(2)计算W1=H3(m1‖ID1‖P1‖R1)。
(3)计算V1=D1+x1·W1+r1·x1·P。
(4)σ1=(R1,V1)。用户 U1对消息m1的签名即为σ1。
1.5 顺序聚合签名
1.5.1 用户 U2签名
(1)用户U2收到用户 U1发来的σ1=(R1,V1)、m1、ID1时,首先计算W1、Q1,即
W1= H3(m1‖ID1‖P1‖R1),
Q1= H1(ID1,P1),
然后验证e(V1,P)=e(PT,Q1)e(W1,X1)e(R1,X1)是否成立。如果等式不成立,则停止聚合签名;如果等式成立,则执行以下步骤。
用户U2的身份为ID2,选取消息m2∈M 和签名密钥D2和x2,具体签名步骤如下:
步骤1 设R1=r1·P,选取一个随机数r2∈,并计算R2,即
R2=R1+r2·P=r1·P+r2·P=(r1+r2)·P。
步骤2 计算W2=H3(m2‖ID2‖P2‖R1)。
步骤3 V1′=V1+r2·X1=D1+x1·W1+(r1+r2)·x1·P;V2′=D2+x2·W2+x2·R2,V2=V1′+V2′。
步骤4 输出聚合签名σ2=(R1,R2,V2)。用户U2对添加消息m2后的聚合签名即为σ2,并将σ2、{m1,m2}、{ID1,ID2}发送给用户 U3。
1.5.2 用户 Ui签名
用户 Ui(i≥3)收到用户 Ui-1发来σi-1=(R1,Ri-1,Vi-1),{m1,m2,…,mi-1},{ID1,ID2,…,IDi-1}时,首先计算Wj、Qj,即
Wj=H3(mj‖IDj‖Pj‖R1),1≤j≤i-1;
Qj= H1(IDj,Pj),1≤j≤i-1。然后验证是否成立。如果等式不成立,则说明前面的签名存在错误;如果等式成立,则说明前面的聚合签名都正确,则用户Ui对消息mi执行以下步骤:
步骤1 设Ri-1=ri-1·P,选取一个随机数,并计算:
Ri=Ri-1+ri·P=ri-1·P+ri·P=
(ri-1+ri)·P。
步骤2 计算Wi=H3(mi‖IDi‖Pi‖R1)。
步骤3Vi-1′=Vi-1+,Vi′=Di+xi·Wi+xi·Ri,Vi=Vi-1′+Vi′。
步骤4 输出聚合签名σi=(R1,Ri,Vi)。
2 方案的安全和效率
为了验证安全性分析结果,本文给出了数论假设,即可计算Diffie-Hellman(CDH)问题为:
∀P,aP,bP∈G1,
2.1 安全性分析
首先在CDH安全假设的条件下对单个签名的安全性进行分析。
定理1 如果攻击者A能以概率ε对单个签名进行伪造,则可以构造一个求解器以相同的概率解决CDH问题。
证明 设攻击者A的一次运行能以概率ε输出对消息m1的伪造签名σ1=(R1,V1),满足验证方程为:
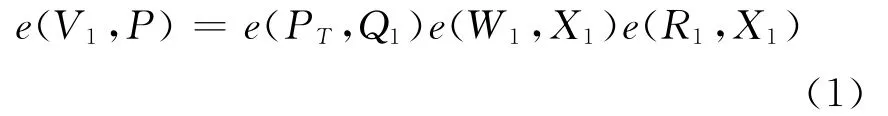
设W1=H3(m1‖ID1‖P1‖R1),将H3(·)视为random oracle,即攻击者必须提交x,才能获取y=H3(x)的值,而不能自行求值,且y的值在H3(·)的值域上随机分布。
因此一次成功的伪造签名必须把m1‖ID1‖P1‖R1作为输入查询H3(·),否则H3(·)在m1‖ID1‖P1‖R1上得到的输出是随机、不可预测的。设m1‖ID1‖P1‖R1出现在攻击者对H3(·)的第i次查询。
现在回卷攻击者状态,在攻击者的第2次运行中保持攻击者对H3(·)的前i-1次查询的回答不变,但重新选取对H3(·)的第i次查询m1‖ID1‖P1‖R1及之后查询的回答。
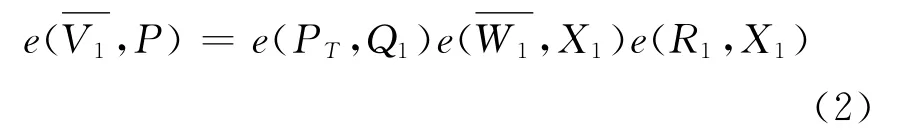
设攻击者第2次运行输出的伪造签名为σ1=(R1,V1),m1,验证方程为:为在第2次运行中对m1‖ID1‖P1‖R1所选取的回答。2个验证方程(1)、(2)相除,可得:
设有一个算法B给定输入为P,aP,bP∈G1,
其中,试图求解CDH问题,即计算abP。
算法B模拟攻击者A的安全试验环境,并回答A发出的random oracle查询,B设置第1个用户的公钥为X1=bP,对H3(·)采取的模拟方法如下:
攻击者提交x,B选取w∈Zp,返回w·(aP)作为H3(x)的值。
第1次运行攻击者时,对m1‖ID1‖P1‖R1,B选取wi∈Zp,设置W1=H3(m1‖ID1‖P1‖R1)=wi·(aP)。
第2次运行攻击者时,B选取wi∈Zp,设置W1=H3(m1‖ID1‖P1‖R1)=wi·(aP),将W1、W1代入方程(3),则有:
e(V1-V1,P)=e((wi-wi)·aP,bP)。故e((wi-wi)-1·(V1-V1),P)=e(abP,P),则abP为(wi-wi)-1·(V1-V1)。
由CDH 假设可知,根据(P,aP,bP,G1)计算abP的结果是不可行的,以上结果与数论假设矛盾,定理得证。
根据顺序聚合的签名过程,每次聚合本质上是将当前签名人生成的独立签名和已有的部分聚合签名进行线性叠加。若一个攻击者A′可以针对某个用户伪造其参与顺序聚合签名,则在顺序聚合签名的某个位置,必然存在一个对该用户的签名伪造,且能通过验证。由上述关于单个签名的安全分析可知,本文构造的顺序聚合签名方案也是安全的。
2.2 效率分析
本文通过计算量和通信量比较2种方案的效率(假设有n个用户参与),结果见表1所列,对于计算代价较小的运算忽略不计。表1中,M为点乘运算;H为Hash函数运算;E为双线性运算。从表1可看出,文献[9]提出的方案和本文方案的计算量是基本相同的。因为本方案对文献[7]中方案的随机数Ri(1≤i≤n)也进行了聚合,在文献[9]方案中需要传输数据{R1,R2,…,Rn},而在本方案中只需要传输R1、Rn即可,所以在通信开销方面本方案是优于文献[9]的。
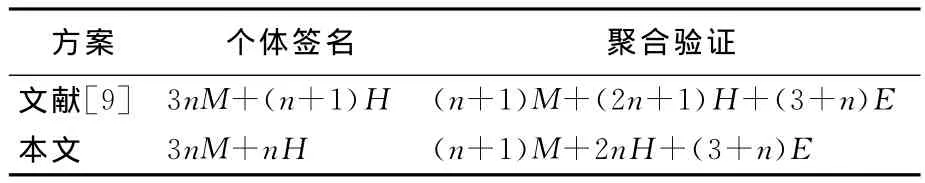
表1 效率比较
3 结束语
本文提出了一种无证书的顺序聚合签名方案,该方案不同于现有的聚合签名方案,因为现有的签名方案大多是无序的,而该方案的签名是有顺序的。本方案的部分密钥生成过程中引入了自认证签名方案,解决了部分密钥的安全问题,同时相对聚合签名,方案的效率也较高。在随机预言模型下证明了该方案可以防止攻击者的伪造攻击。
[1] 薛益民,米军利.可撤销匿名性的盲代理群签名方案[J].合肥工业大学学报:自然科学版,2013,36(12):1465-1467.
[2] Boneh D,Gentry C,Lynn B,et al.Aggregate and verifiably encrypted signatures from bilinear maps[C]//Advance in Cryptology-EUROCRYPT 2003,Warsaw,Poland.Berlin:Springer,2003:416-432.
[3] Lysyanskaya A,Micali S,Reyzin L,et al.Sequential aggregate signatures from trapdoor permutations[C]//Advances in Cryptology-EUROCRYPT 2004,Interlaken,Switzerland.Berlin:Springer,2004:74-90.
[4] Shamir A.Identity-based cryptosystems and signature schemes[C]//Advances in Cryptology:Proceedings of CRYPTO 84.Berlin:Springer,1985:47-53.
[5] Al-Riyami S S,Paterson K G.Certificateless public key cryptography[C]//Advances in Cryptology-ASIACRYPT 2003,Taipei,Taiwan.Berlin:Springer,2003:452-473.
[6] Gong Zheng,Long Yu,Hong Xuan,et al.Two certificateless aggregate signature from bilinear maps [C]//Eighth ACIS International Conference,2007:188-193.
[7] 曹素珍,王彩芬,程文华,等.一种高效的无证书聚合签名方案[J].计算机工程,2011,37(18):157-159,166.
[8] Li Fengyin,Liu Peiyu.An efficient certificateless signature scheme from bilinear parings[C]//Network Computing and Information Security(NCIS),2011:35-37.
[9] Zhang Lei,Zhang Futai.A new certificateless aggregate signature scheme[J].Computer Communications,2009,32(6):1079-1085.
[10] Shao Zuhua.Self-certified signature scheme from pairings[J].The Journal of Systems and Software,2006,80(3):388-395.

