对数周期天线阵波束形成的最优激励研究

尹 凡， 孙玉发

（安徽大学 电子信息工程学院，安徽 合肥 230601）

尽管由于卫星通信的出现及迅速发展，短波通信曾一度停滞不前，但近年来短波通信又重新引起了关注，它是海上通信、极地通信的重要手段，也是军事通信的重要战略备份。目前短波通信技术已经取得了重大进展，广泛地采用扩频、跳频和实时信道估值（RTCE）等新技术，这使得短波通信成为远程通信的重要手段。为了实现远程的点对移动点的通信，就需要根据移动点的运动以及电离层的变化，改变发射天线波束的方位和仰角。因此，这就要求天线部分是短波相控阵系统。

为获得理想的通信效果，提高天线阵的效率和方向性是提高系统灵敏度的有效途径。为了提高整个天线阵的增益，单元天线就希望选择高增益定向天线。短波宽带天线一般有2种较成熟的天线形式：一种是菱形天线，另一种是对数周期天线。对数周期天线工作频带宽，由于其特有的结构，其辐射特性与驻波天线相似，其效率可达80%以上，增益一般可达7～10dB［1－2］，占地面积小。因此，对数周期天线是一较好的选择。对数周期天线近年来也获得进一步的开发和应用，文献［3］提出一种Koch阵子的对数周期天线，进一步缩小天线的尺寸；文献［4］考虑到对数周期天线辐射脉冲失真问题，从传递函数开始进行设计，满足脉冲UWB的应用；文献［5］将目前热门的超材料应用于对数周期天线设计，实现正负相移，进一步提高了UWB脉冲辐射的保真度。

对数周期天线阵由于存在阵子之间、单元天线之间的耦合，要获得需要的波束指向、最大增益，激励信号的确定成为一个关键问题。本文利用矩量法对特殊要求的对数周期天线阵进行全波分析，对天线阵单元天线之间的互阻抗、驻波比以及最优激励等进行了严格的计算和分析。其结果表明该天线阵具有非常好的性能，其得到的结果对天线阵的设计和分析具有参考价值。

1 单元天线和天线阵的结构

对数周期偶极子天线（LPDA）的结构示意图如图1所示［6］。

图1 偶极子对数周期天线原理结构示意图

单元对数周期天线由N个平行排列的对称振子构成，其结构特点是各振子的尺寸、位置与振子的序号有关，即按照结构周期τ组成。令

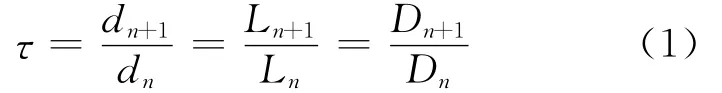
其中，n为振子的序号，n＝1，…，N；dn为两相邻阵子的间距；Ln为振子的长度；Dn为天线的几何顶点到振子的垂直距离。所有振子采用一对传输线进行馈电，源接在短振子的一端，两相邻振子交叉馈电。天线的整体结构决定于τ和α，α为振子的末端连线夹角。在实际设计天线时，为了方便，引入一个参量σ，σ＝dn／（2Ln），称为间隔因子。σ、α、τ之间的关系如下

在确定天线设计参数时，只要知道σ、α、τ中的任意2个，则天线的几何结构及其相应的电特性也就确定了。为了达到天线阵的工作频率范围为4～12MHz，本文的单元天线参数为τ＝0.88，α＝370，N＝12，σ＝0.09。天线阵采用八单元的对数周期天线，结构布局如图2所示，其中β1＝75°，β2＝55°。天线阵采用水平极化，为了防止地面镜象对宽带工作的影响，每一单元天线对地面有一倾角γ＝31°，天线的架高最高处为30m，这样高频辐射区离地面近，低频辐射区离地面远，可以确保各阵子相对地面的电长度一致。采用这种斜架和扇形布局方式，天线阵的天波工作频带可达3～5倍频程。

图2 对数周期天线阵列位置的俯视图

2 对数周期天线阵的矩量法分析

2.1 基本原理

电磁场的反应积分方程［7］为：

其中，Em、Hm为检验源产生的场；Js＝n×H，Ms＝－n×E为由等效原理得到的天线振子表面的等效电流和等效磁流；Ji、Mi为天线阵馈入的电流和磁流。假设天线的振子由理想导体构成，则Ms＝0；馈源采用磁流环模型，则Ji＝0；这样（3）式可简化为：

（4）式即是所要求解的算子方程。本文采用分域正弦基的Galerkin算法。

2.2 单元天线激励的处理

单元对数周期天线具有多个交叉馈电的振子，而激励信号只有1个，因此一般采用将矩量法和等效传输矩阵网络相结合的方法［2，8］来处理。如图3所示，把对数周期天线分成天线阵网络和集合线网络，分别把这两部分看作N端口无源网络。采用矩量法求解天线阵网络的各端口的互阻抗矩阵，利用两端口网络方程计算集合线网络阻抗或导纳矩阵。运用集合线网络、天线阵网络和矩量法分段电流的内在联系，把天线阵网络和集合线网络有机结合起来，由天线激励电流直接给出简洁的天线电流分布表达式。

图3 LPDA的2个等效网络

为了求解LPDA上的电流分布必须先求出激励每个振子的电压UA。令YA和ZA分别代表天线阵网络的导纳矩阵和阻抗矩阵，则电压、电流之间的关系为：

其中，UAi、IAi分别为第i个振子的输入端电压和电流；ZAii、ZAij分别为输入端的自阻抗和互阻抗（i，j＝1，2，…，N）。

用矩阵表示为：

令YL表示传输线网络的导纳矩阵，IL、UL表示具有N端的网络每个输入端上的电流和电压矢量。利用网络理论，集合线各端子处电压UL、电流IL之间的关系为：

传输线网络的导纳矩阵可表示为：

其中，Y0为传输线的特性导纳；k为传输线的传输常数；di为振子之间的距离。由图3可知，UA＝UL。因此，2个并联网络总的电流表达式为：

其中，Is为激励电流向量，它只有最后一个元素有值，其他元素为0。在具体的分析过程中，将对数周期天线的所有振子进行剖分，总共得到NN段（其中每一个振子上的分段数应保证为偶数，模为奇数），则由矩量法，天线上各个分段的电流、电压可以归结为如下方程：

其中，UM、IM分别为NN维的电压列向量和电流列向量；ZM为NN阶的阻抗矩阵。现在的主要任务是求出YA的分布，利用YA得到电流分布，求得其他的各种电参数。因为天线阵的每个振子都是中心馈电，显然，UM只在每一个振子的中心点所对应的元素组成的向量就是UA。为了求解出天线上的电流，定义一个扩展矩阵P，P为NN×N矩阵，每一行都有且仅有一个非零元素1，依次位于馈电点对应模的列，则有：

综合以上各式，可得：

PTZ－1MP即相当于天线阵馈电端的导纳矩阵，这样就可以求出YA。再由（8）式、（10）式，可得天线上的电流分布：

以上是对单元对数周期天线的分析过程，ZM是利用矩量法分析对数周期天线时得到的阻抗矩阵，可以求解，如果是分析对数周期天线阵列，则在计算阻抗矩阵ZM时，必须考虑非共面振子之间的互阻抗的计算。

2.3 天线阵互阻抗矩阵的计算

从图2可以看出，要计算对数周期天线阵的各振子上的电流分布，需要对图3所示的2个网络的合成，其中天线部分的网络是存在相互耦合的，因此，不是简单的组合。由于不同对数周期天线的振子之间是非共面的，这样计算互阻抗矩阵不同于单元对数周期天线。下面给出非共面模之间的互阻抗的计算［9］。空间任意2个振子间的位置关系如图4所示。

假设振子1的两臂长为2d1，沿着Z轴放置，馈电点位于坐标原点，若I1（0）为其输入端电流，则沿线电流分布的表达式为：

振子2的臂长为2d2，振子中心位于（x0，y0，z0），若I2（0）为其输入端电流，则

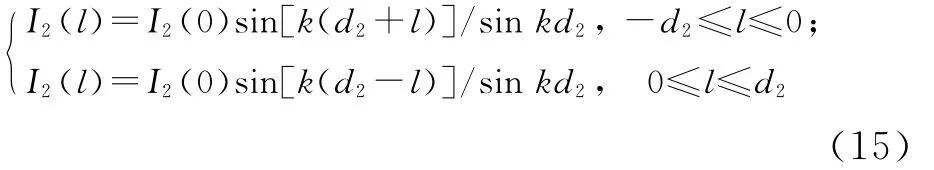
振子2的电流I2的方向矢量为：

l＝lxex＋lyey＋lzez。

图4 空间任意2个振子间的位置关系

根据反应积分方程，振子1、2之间归一化于输入电流的互阻抗为：

其中，E21（s）为振子1在2上产生的电场，在柱坐标系中，E21（r）＝E21ρeρ＋E21ez，其中

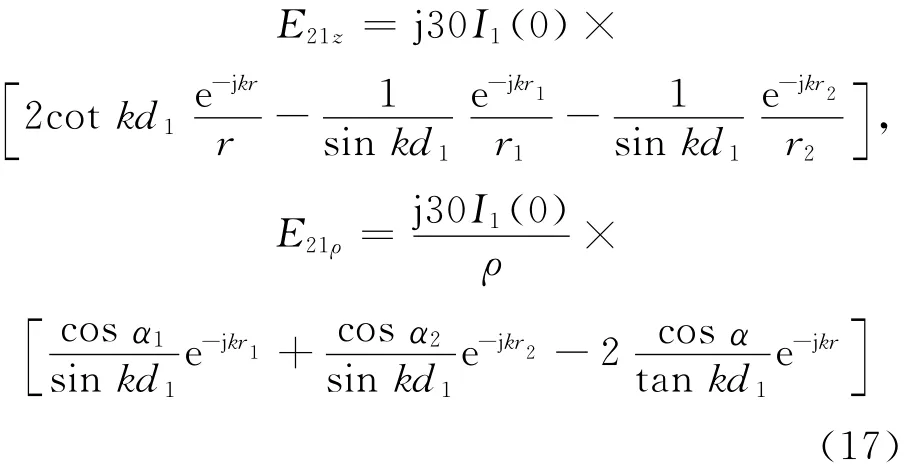
将（17）式转换成直角坐标系代入（16）式，并运用数值积分就可以得到任意两模之间互阻抗。

从图2可以看出，在计算互阻抗矩阵时，除了可以利用互阻抗矩阵的对称性，节约1／2的计算量外，还可以利用天线阵布局本身的对称性。在阵列中1、4，2、3，5、8，6、7单元天线分别关于Y轴对称。因此，稍加分析可以发现，只要计算出1单元和2单元天线与其他单元天线的互阻抗，就可以计算出整个互阻抗矩阵。

3 对数周期天线阵的最优激励

在天线设计中，如何确定使天线获得最佳性能时所对应的激励，是一个很基本的问题。目前很多关于阵列问题的求解中，一般忽略了阵列中各单元之间的互耦。而这里将要讨论的是考虑了阵元间互耦后，阵列获得最佳性能时的激励。任意天线阵及其远区检验天线如图5所示。

图5 任意天线阵及其远区检验天线

图5a所示为假设一任意的N端口天线阵以及位于远区的一个接收天线，假设接收天线可以接收正交极化分量。天线阵加上接收天线构成了一个N＋2端口网络，Vt1代表接收的水平极化分量，Vt2代表接收的垂直极化分量。利用开路阻抗矩阵，可以得到：

其中，Vt、It为接收天线的端口电压和电流；Va、Ia为阵列各端口的电压、电流向量；Ztt为接收天线的输入阻抗，由于接收正交分量之间不耦合，所以它是1个2×2的对角阵；Zaa为天线阵的阻抗矩阵，它可以通过前面求得的天线阵的模式互阻抗矩阵，提取对应激励单元的行与列得到；Zat、Zta为接收天线和天线阵之间的互阻抗矩阵，假设接收天线是一理想的无方向性天线，由于接收天线与天线阵距离很远，因此Zat（1，i）的大小与天线阵的第i阵元在接收点水平场强大小成正比，Zat（2，i）的大小与天线阵的第i阵元在接收点垂直场强大小成正比，这样就可以通过前面计算的天线阵的模式互阻抗矩阵，计算出第i阵元激励时，整个天线阵上的电流分布，根据电流分布计算出接收方向的场强，从而得到Zat或Zta。

假定阵列所加的激励电流源为I1，I2，…，IN，接收天线开路，如图5所示，此时的复输入功率可以表示为：

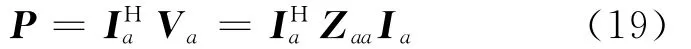
所以加在阵列上的输入功率是（19）式的实部。

而接收天线端口电压模的平方正比于入射场的功率密度。由（18）式，令It＝0，则接收天线方向的天线阵发射的功率密度可以表示为：

其中，K为取决于接收天线自身的常数。比较（20）式与（21）式，可以得到阵列在接收方向的增益［10］为：

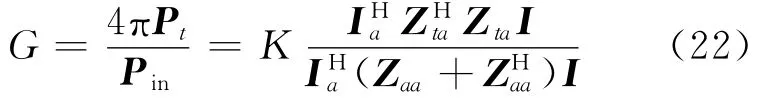
从（22）式可看出G具有厄密特二次式，所以令：

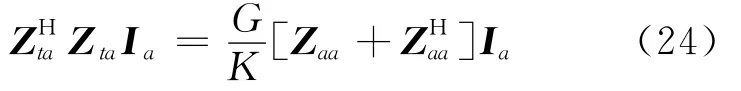
可以得到一个特征值方程：其中，G／K为特征值，由阻抗矩阵的性质，［Zaa＋］为正定阵，为半正定阵，即所有的特征值大于等于0。因此，最大的特征值对应的特征向量即是获得最大功率增益所需要的激励电流。

这种激励是以最大增益为优化目标求得的最优激励电流，不仅相位不同，而且幅度也不同。实际的天线阵系统的各单元的激励电流输出能力一致，这样不等幅激励会产生资源的闲置，因此，另一种优化目标就是使得接收方向获得最大的接收强度。由（21）式，就是使Pt获得最大。根据上面的分析只有2个非零的特征值。由矩阵的特征分解：

由（25）式可见，在各激励单元幅度受到约束，Ia的相位矢量与的相位矢量一致的情况下，获得最大的输出功率。

4 计算结果与分析

通过以上的理论分析，利用Matlab编程开发了上述矩量法分析计算程序，对本文开始给出的天线阵结构进行了计算。由于天线架设较高，地面近似按理想导体镜象来处理，由于单元天线的各振子离地面不是等高的，因此不能简单地乘以天线阵镜象因子，而是利用各个子域模的电流镜象来完成。实际计算时将每个单元对数周期天线剖分成122子模，共计976模。采用最大输出功率作为优化目标。此时得到的所有端口所加的激励是等幅不同相的，且以第8单元的相位为参考，令其为0。

表1、表2分别列出了天线阵设计的2端频率点4、12MHz，波束指向不同方向时激励信号的相位、各单元天线的驻波比和天线阵的增益。从计算结果可以看出，除个别点驻波比超过2外，基本上都控制在2以内，增益都达到23～26dB。这是一般短波不可能做到的。

另外，图6a所示为f＝6MHz、θ＝40°，即仰角为500时，天线阵在方位上扫描±300方向图，图6a表明阵列的主波束在方位上方向是精确可控的。图6b所示为f＝6MHz、φ＝270°，仰角为70°、50°、30°（即θ为20°、40°、60°）波束扫描的方向图，从图6b中可以看出，仰角最大值与预设方向有很小的偏差，同时可以发现，仰角越高天线阵的增益越低，这都是因为地面镜象的影响所致。

由上述计算结果可知，该天线阵可以满足方位±150、仰角300～600的电扫描，增益可达23dB以上，天线阵的主波束在方位和仰角上方向都基本是精确可控的。

以电离层高度为300km计算，该天线阵的落地波束方位前后左右都能达到100km，通过相控扫描前后可达300～1 500km，左右可达±400km，因此该天线阵在远洋通信中将有非常大的应用价值。

表1 4MHz时不同波束指向对应的阵列激励相位、驻波比和增益

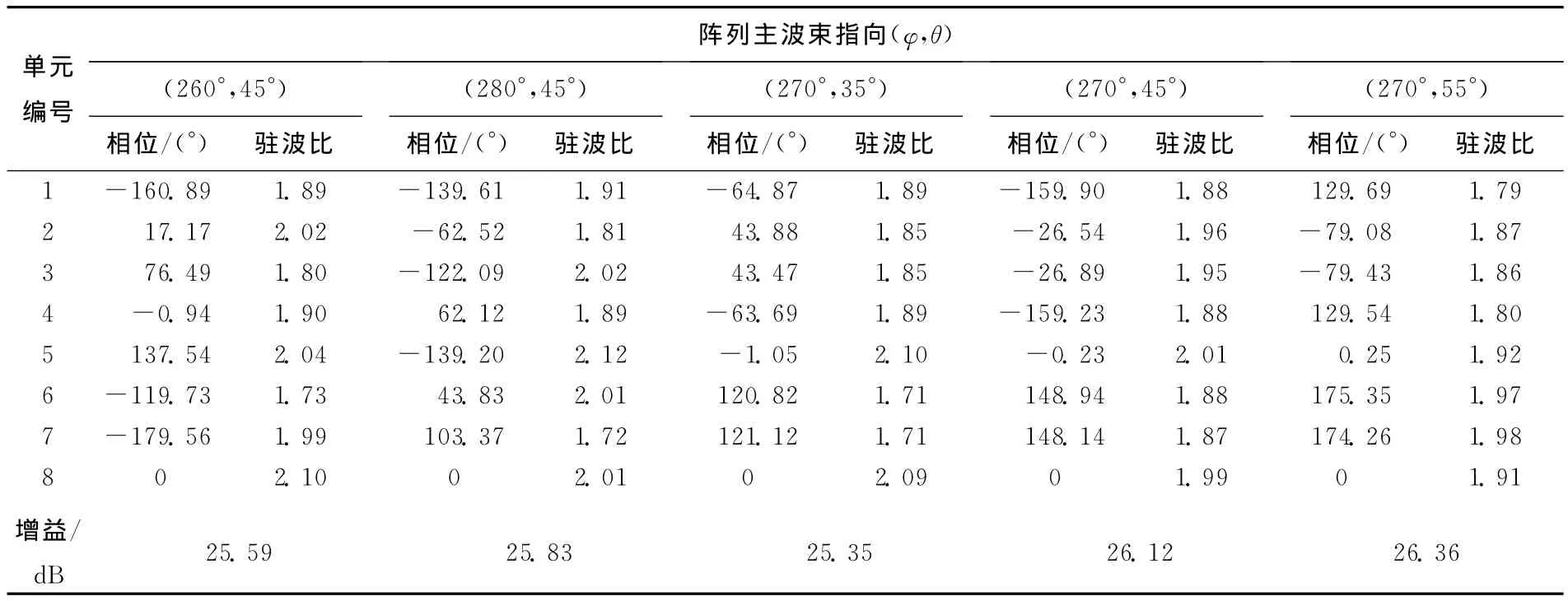
表2 12MHz时不同波束指向对应的阵列激励相位、驻波比和增益

图6 6MHz时方位角、仰角扫描的方向图

5 结束语

本文利用矩量法结合微波网络的全波理论对对数周期天线阵进行了严格的理论分析和数值计算，计算对数周期天线阵的工作状态的输入阻抗、驻波比电特性参数，同时计算分析了天线阵的波束宽度、波束指向和增益辐射特性参数，在此基础上对天线阵的波束扫描在最大增益和最大功率2个优化准则下的最优激励进行了理论分析和数值计算，证明了算法的有效性。本文方法对复杂线天线阵的分析具有一定的指导意义，同时在远洋、极地等超视距通信中有应用价值。

［1］ 周朝栋，王元坤，周良明.线天线理论与工程［M］.西安：西安电子科技大学出版社，1988：294－320.

［2］ Peixeiro C.Design of logic－periodic dipole antennas ［J］.IEE Proceedings，1998，135（2）：98－102.

［3］ Anagnostou D E，Papapolymerou J，Tentzeris M M，et al.A printed log－periodic koch－Dipole array （LPKDA）［J］.IEEE Antenna and Wireless Propagation Letters，2008：7（1）：456－460

［4］ Merli F，Zürcher J F，Freni A，et al.Analysis，design and realization of a novel directive ultrawideband antenna［J］.IEEE Transaction on Antennas and Propagation，2009，57（11）：3458－3466.

［5］ Ziolkowski R W，Peng Jin.Metamaterial－based dispersion engineering to achieve high fidelity output pulses from a log－periodic dipole array ［J］.IEEE Transaction on Antennas and Propagation，2008，56（12）：3619－3629.

［6］ 斯塔兹曼，蒂尔.天线理论与设计［M］.朱守正，安同一，译.第2版.北京：人民邮电出版社，2006：241－251.

［7］ 胡 庆，高 荣，肖 琴，等.高效偶极矩法分析金属天线电磁辐射特性研究［J］.合肥工业大学：自然科学版，2012，35（5）：648－651.

［8］ 袁伟良，梁昌洪，史小卫.矩量法结合网络理论分析对数偶极天线［J］.微波学报，2000，16（2）：106－110.

［9］ Richmond J H，Gerry N H.Mutual impedance of nonplannar－skew sinusoidal dipoles［J］.IEEE Transaction on Antennas and Propagation，1970，18（1）：412－414.

［10］ Harrington R F.Antenna excitation for maximum gain［J］.IEEE Transaction on Antennas and Propagation，1965，13（6）：896－903.