基于改进遗传算法框架结构损伤识别
李 慧, 丁万宁, 周明姬, 王二成
(1.邯郸学院 信息工程学院,河北 邯郸 056005;2.河北工程大学 土木工程学院,河北 邯郸 056038)
结构在投入使用后,会受到周围环境的影响,或遭受地震、冲击等外部偶然荷载的作用,同时也由于材料本身力学性能的变化,在使用一定的年限后,通常需要对结构进行检测,来评价内部的损伤情况[1-2]。对于结构整体的性能,通常要通过在既定荷载作用下结构的静态或动态响应来评价系统参数,动态测试相对于静态测试对结构进一步损伤的可能性小,是主要的测试手段。损伤分析主要是通过结构的固有参数与响应之间的关系,由所测响应反推结构的性能参量,其实质是参数识别问题,可以通过优化算法来求解[3-5]。
遗传算法是一种智能优化算法[6],不涉及复杂的数学知识,不要求函数可导、连续等性质,可以处理复杂的目标函数和约束条件,广泛应用到各个领域处理各种优化问题[7-11],对于处理系统辨识、损伤识别也显示出很大的优越性。
文献[12]采用贝叶斯理论和改进的免疫遗传算法对结构进行了损伤识别;文献[13]采用遗传算法对振动体进行损伤检测;文献[14]采用改进遗传算法对两端固支梁进行了损伤诊断;文献[15]介绍了利用遗传算法如何进行结构损伤识别及程序设计,并对三跨连续梁进行了损伤分析;文献[16]采用递阶遗传算法对结构进行了多损伤监测;文献[17]利用改进损伤识别因子和遗传算法研究了在噪声影响下的结构损伤识别,并以简支梁和连续梁为例进行了识别效果验证。文献[18-20]探讨将遗传算法等智能优化算法用于对结构的损伤识别。
遗传算法具有思路清晰、操作简单等优点,但存在着收敛速度慢、出现“早熟”、陷入局部最优等问题。本文针对基本遗传算法在收敛的过程中由于交叉或变异可能破坏原本已经搜索到的父代较优个体,将选择算子、交叉算子和变异算子分别施加在父代群体上,然后对新产生的个体进行优劣排序,择优作为新一代群体,从运算流程上提高算法的寻优效率,并将改进后的算法运用到框架结构的损伤识别中。
1 框架结构损伤识别
1.1 结构损伤识别方法及原理
组成结构的某个构件发生损伤会引起整个结构的刚度等力学参数发生变化,表征结构动态特性的固有频率和对应的振型也会发生变化。固有频率和振型与结构的质量分布和刚度是密切相关的。假定损伤只是刚度的退化,直接测定结构的刚度是比较困难的,静态的测定方法还可能进一步引起内部损伤破坏,因此,通常通过测定结构的动态信号来反推某个位置处构件的刚度是否发生变化及严重程度。
假定结构为n个自由度系统,n为正整数,未损伤状态下,质量矩阵为M,通常为对角阵,刚度矩阵为K,即


相对应n个固有频率为ω1,ω2,…,ωn,n个振型向量为φ1,φ2,…,φn,其中φi=(φi1,φi2,…,φin)。结构发生损伤,刚度发生变化,由原来的刚度矩阵K变为K′,即

其中,αij为对应刚度矩阵元素中kij的损伤因子,0<αij≤1。
αij的取值不同,对应kij的损伤程度不同。当αij接近0时,指损伤很严重,该段将退出工作;当αij=1,说明该位置没有损伤。
基于动态测试信号的损伤识别,已知结构的原刚度矩阵K,假设损伤因子为αij,得到损伤后的刚度矩阵K′,假定质量矩阵M不变,则

计算求得损伤后的固有频率为ωc1,ωc2,…,ωcn,相对应振型为φc1,φc2,…,φcn。
同时结构模态试验测量得出损伤后结构的固有频率和振型分别为ωm1,ωm2,…,ωmn和φm1,φm2,…,φmn。
确定损伤因子αij,使得计算得到的动态特性参数无限接近于测量值,就是损伤识别的过程。
1.2 框架结构损伤识别目标函数
假设n层的框架结构如图1所示,自下而上每层水平刚度分别为k1,k2,…,kn,通常采用集中质量法,将质量集中在楼层处,分别为m1,m2,…,mn。

图1 框架结构示意图
质量矩阵M为对角阵,主对角线上元素为各层质量,其他元素均为0,刚度矩阵K为:
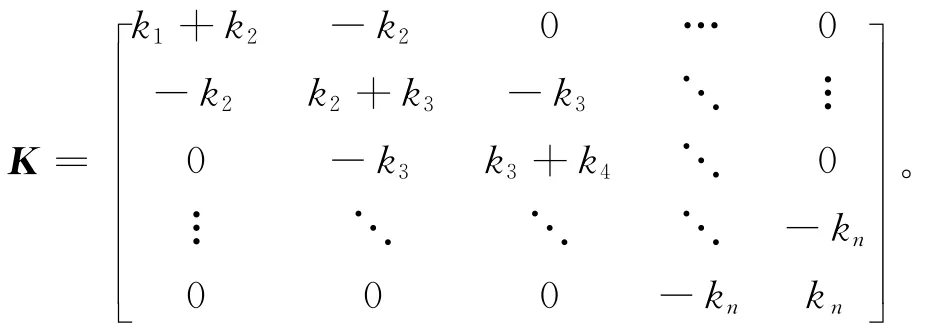
为了更直观可见,物理意义更明确,也可以直接对水平层间刚度进行折减表示损伤,损伤后的层刚度系数分别为α1k1,α2k2,…,αnkn,代入原刚度矩阵K,得到损伤后的刚度矩阵K′。
此时,损伤识别问题就是确定损伤因子αi,使得计算出的动态特性参数与测量值相吻合。这是一个选优过程,目标函数如下:

其中,ai为第i阶固有频率权值;bi为第i阶振型向量权值;MAC()指模态置信度准则。
约束条件:

2 改进遗传算法及程序实现
2.1 遗传算法流程改进
基本遗传算法的运算流程如下:
(1)根据设计变量生成初始种群,由N个个体组成,N为一正整数。
(2)计算个体适应度值,对不符合约束条件的个体,施加惩罚算子。判断是否满足终止条件,满足,结束;否则,进入步骤(3)。
(3)对个体施加选择算子,适应度值高的个体具有更高的概率被选择进入到下一步。
(4)施加交叉算子。
(5)施加变异算子,返回步骤(2)。
在基本遗传算法中,选择、交叉和变异算子是串联关系。当交叉率和变异率取值过大,后续操作算子会破坏已经搜寻到的较优个体;反之,如果交叉率和变异率取值过小,收敛速度会变慢。据此改进遗传算法,改进后的遗传算法流程如图2所示。
改进后的优化计算流程中,将父代中的个体在施加操作算子之前先自身复制2份,对每一份分别进行选择、交叉和变异操作,然后对这3N个个体汇总,适应度计算并排序,选择较优的前N个个体作为子代。此时,交叉率和变异率可以取100%,不会使父代中搜寻到的较优个体被后续操作算子破坏,最大限度地保存了最优个体。

图2 改进遗传算法流程
2.2 惩罚算子改进
如果父代中个体差异性不大或在解空间中分布过于集中,则算法很可能会陷入某一局部最优解。因此,除了对不满足约束条件的个体施加惩罚函数外,对群体中具有过高相似度的个体也施加惩罚算子,保存最优个体,降低其他个体的适应度值。个体的相似性用两者的海明距离来表示,假设2个个体分别为Xi和Xj,它们的染色体的长度为m,则它们之间的海明距离为:

控制变量之间的海明距离可以提高算法的分布性和收敛性[21],在操作的过程中,染色体中各设计变量可能存在数量级上的差别,为了使惩罚算子更有效,衡量两者的差异性可以采用(7)式:当dis(Xi,Xj)<L时,比较2个个体的适应度的大小,并对其中适应度较低的个体处以惩罚函数:

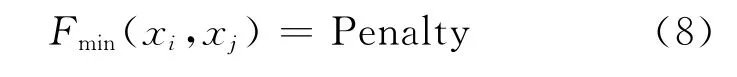
3 算例分析
3.1 框架模型
某3层钢框架结构如图1所示,m1=m2=m3=1.5×106kg,k1=10.0×106N/m,k2=9.5×106N/m,k3=9.0×106N/m。
质量矩阵为:

刚度矩阵为:

3.2 单变量损伤识别
现假定对应层刚度损伤因子α1=1,α2=0.5,α3=1,即2层的水平向层刚度系数折半,质量矩阵M不变,原刚度矩阵变为:

根据(1)式,利用Matlab软件进行计算得出,ω1=0.966 4rad/s,ω2=3.001 1rad/s,ω3=3.880 6rad/s,相对应的振型列向量为:
φ1= (1 2.810 4 3.328 4)T,φ2= (1 0.261 0 -0.520 8)T,φ3= (1 -1.650 3 1.093 0)T。
将以上损伤后的频率和振型作为测量值,根据(2)式和图2的流程,在VC++环境下,编制C语言程序,利用改进遗传算法反求损伤因子α1、α2、α3,取值为一位数,加权系数均取1,初始种群规模为100,优化收敛过程如图3所示。

图3 单变量损伤识别收敛
从图3中可以看出,经16次迭代运算,收敛到最优解,对应最优个体为:
X= (α1α2α3)= (1.0 0.5 1.0)。
可见,对于单变量损伤识别,改进遗传算法具有很好的全局寻优能力,多次试算,最优解稳定。与基本遗传算法相比,解更稳定,收敛速度更快。设定最大代数为100,各方案结果见表1所列。表1中,方案1,操作算子串联;方案2,操作算子串联+保持个体差异惩罚算子;方案3,操作算子并联;本案,操作算子并联+保持个体差异惩罚算子。表2中方案含义同此。
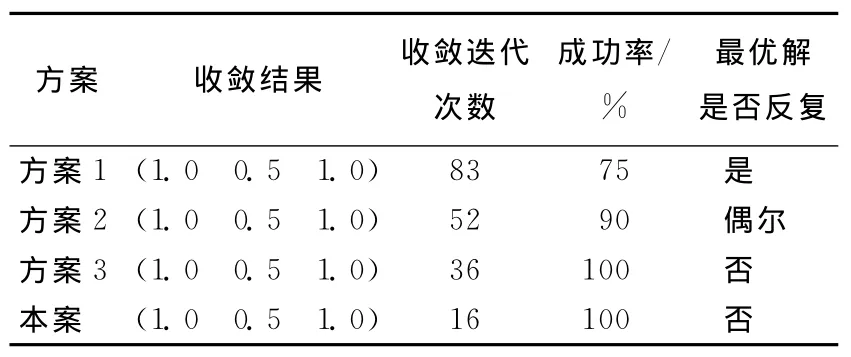
表1 单变量损伤识别多种算法结果比较
3.3 多变量损伤识别
假设框架各层刚度均有损伤,α1=0.6,α2=0.7,α3=0.8,即损伤后的框架各层刚度分别为原来的60%、70%和80%,刚度矩阵变为:
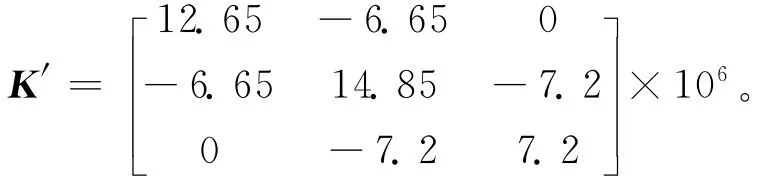
计算得损伤后频率ω1=0.913 9rad/s,ω2=2.633 1rad/s,ω3=3.833 8rad/s,相对应的振型列向量为:
φ1= (1 1.713 8 2.074 9)T,φ2= (1 0.338 4 -0.761 5)T,φ3= (1 -1.413 1 0.685 3)T。
同样,将以上固有频率和振型作为测量值,利用遗传算法求损伤因子α1、α2、α3。优化收敛过程如图4所示。
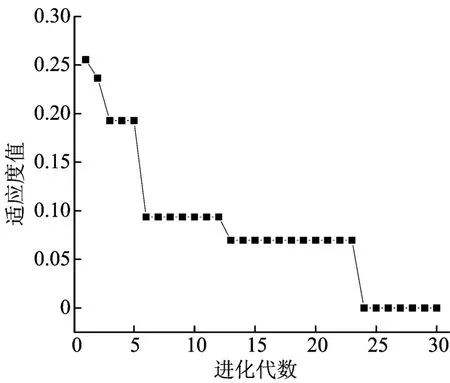
图4 多变量损伤识别收敛
最后收敛到最优解为:
X= (α1α2α3)= (0.6 0.7 0.8)。
同等条件下与其他算法的结果对比见表2所列。
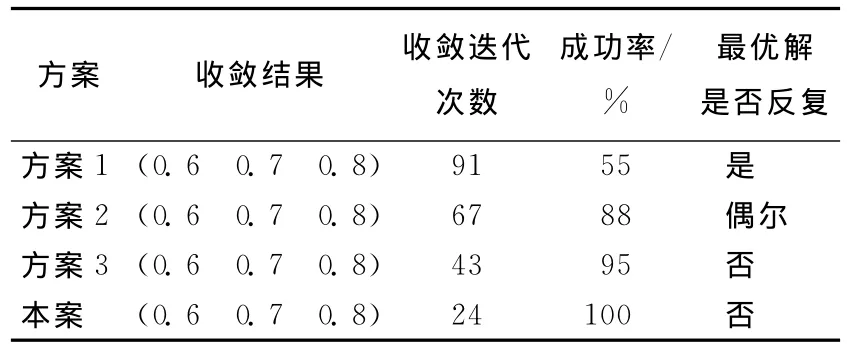
表2 多变量损伤识别多种算法结果比较
从以上2个算例可以看出,无论是单变量损伤还是多变量损伤,改进遗传算法的优化收敛过程是相似的,都能很好地识别结构的损伤位置及损伤程度。
实际工程中进行损伤识别时,已知结构的原质量矩阵和刚度矩阵,通过动态测试得出结构的固有频率和振型,假设各刚度系数损伤因子,按上述方法采用遗传算法进行寻优计算,对结构损伤情况给出评价。
4 结 论
(1)改进遗传算法用于框架结构的损伤,能较好地识别出结构的损伤位置和损伤程度。
(2)通过改变运算的流程能保证最优解不会出现反复,提高收敛的效率。
(3)通过施加惩罚算子来保持个体的差异性能有效地防止算法“早熟”及过早陷入局部最优解。
[1] 杨秋伟.基于振动的结构损伤识别方法研究进展[J].振动与冲击,2007,26(10):86-91.
[2] 郭惠勇,李正良,彭 川.结构损伤动力识别技术的研究与进展[J].重庆建筑大学学报,2008,30(1):140-145.
[3] Zheng Z D,Lu Z R,Chen W H,et al.Structural damage identification based on power spectral density sensitivity analysis of dynamic responses[J].Computer &Structures,2015,146(1):176-184.
[4] Andrzej K.Vibration based spatial damage identification in honeycomb-core sandwich composite structures using wavelet analysis[J].Composite &Structures,2014,118(11):385-391.
[5] Cao Maosen,Radzienski M,Xu Wei,et al.Identification of multiple damage in beams based on robust curvature mode shapes[J].Mechanical Systems and Signal Processing,2014,46(2):468-480.
[6] 周 明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999:4-17.
[7] 汪 权,王建国,陈 涛,等.高层建筑结构地震反应的分散遗传-模糊控制研究[J].合肥工业大学学报:自然科学版,2012,35(9):1230-1234.
[8] 张代胜,张 旭,李彦保,等.基于Pareto聚类免疫进化算法的发动机悬置系统优化与稳健性分析[J].合肥工业大学学报:自然科学版,2012,35(12):1589-1593.
[9] 李志强,何明胜,夏多田.基于层次分析遗传算法的SRC框架梁优化设计[J].合肥工业大学学报:自然科学版,2014,37(5):609-614.
[10] 扈 静,蒋增强,葛茂根,等.基于改进遗传算法的混合装配生产线平衡问题研究[J].合肥工业大学学报:自然科学版,2010,33(7):1006-1009,1019.
[11] 褚永康,文桂林,崔 中,等.基于遗传算法的汽车变速箱轻量化设计[J].合肥工业大学学报:自然科学版,2011,34(10):1461-1465.
[12] Guo H Y,Li Z L.Structural damage identification based on Bayesian theory and improved immune genetic algorithm[J].Expert Systems with Applications,2012,39(7):6426-6434.
[13] Rao M A,Srinivas J,Marthy B S N.Damage detection in vibrating bodies using genetic algorithms[J].Computer&Structures,2004,82(11):963-968.
[14] 易伟建,刘 霞.基于遗传算法的结构损伤诊断研究[J].工程力学,2001,18(2):64-71.
[15] 朱劲松,高嫦娥,肖汝诚.基于遗传算法的结构损伤识别及其程序设计[J].哈尔滨工业大学学报,2007,39(12):1952-1956.
[16] 范德礼,郑世杰,王宏涛.基于递阶遗传算法的结构多损伤监测[J].航空动力学报,2013,28(9):2050-2054.
[17] 黄民水,吴 玏,朱宏平.噪声影响下基于改进损伤识别因子和遗传算法的结构损伤识别[J].振动与冲击,2012,31(21):168-174.
[18] 王延伟,宋旭坤,温瑞智,等.智能优化算法在结构损伤识别中的应用[J].世界地震工程,2011,27(4):44-51.
[19] 张瑞刚,郭 利,王天辉,等.运用改进的量子遗传算法进行结构损伤识别[J].噪声与振动控制,2013,33(3):203-207.
[20] 郭惠勇,李正良.免疫遗传算法在结构损伤识别中的应用与改进[J].土木建筑与环境工程,2012,34(2):7-14.
[21] 谭 阳,谭岳武,唐钊轶.基于海明差异评价的多目标进化算法[J].计算机工程,2014,40(2):212-218.

