一种多标记学习入侵检测算法

钱燕燕， 李永忠， 章 雷， 余西亚

（1.江苏科技大学 计算机科学与工程学院，江苏 镇江 212003；2.紫光软件系统有限公司，北京 100084；3.南京邮电大学通达学院，江苏 南京 210003）

入侵检测技术［1］是网络安全防御体系的关键技术之一，主要分为异常检测和误用检测2类。其中异常检测有检测新型攻击的能力，且不需要有入侵的先验知识，其关键是建立系统的正常行为模式及利用该模式去检测和判断系统的异常行为。入侵检测方法结合一些智能技术应用于入侵检测系统中成为当前研究的重点。文献［2］提出了基于混合分类模型的入侵检测技术；文献［3］提出云模型半监督聚类动态加权的入侵方法；文献［4］提出基于混合入侵检测技术的网络入侵检测方法等。

多标记学习（multi－label learning）是机器学习一个新的研究领域，已经成功应用在文档分类［5］、图像分类［6］、生物基因功能分类［7］等领域。本文研究了基于多标记学习的KNN（multi－label k－nearest neighbor，ML－KNN）算法，进行了必要的改进，使其能对入侵检测KDD CUP99数据集进行分类，并建立正常行为模式，再利用该模式去检测和判断系统的异常行为，然后将结果与基于聚类的入侵检测方法进行比较。实验证明，本文方法具有高检测率和低误报率，在一定程度上能够改善入侵检测的性能。

1 多标记学习

1.1 问题定义

假设X＝Rd代表d维的示例空间，Y＝｛y1，y2，…，yq｝表示q个类别的标记空间。传统的监督学习框架是单示例单标记学习［8－10］，即1个对象只用1个示例来表示，而且该示例只对应1个类别标记。学习的主要目标是从数据集｛（x1，y1），（x2，y2），…，（xm，ym）｝中可得函数f：X→Y，其中，xi∈X为一个示例；yi∈Y为示例xi对应的类别标记。

在多标记学习中，1个对象用1个示例表示，且该示例可以同时对应多个类别标记［7，10］。给定多标记训练集T＝｛（x1，Y1），…，（xm，Ym）｝（xi∈X，Yi∈Y），其中，X为输入空间；有限个标记的集合Y＝｛1，2，…，Q｝。多标记学习系统的目标是从训练集T中进行学习，输出一个多标记分类器h：X→2Y。一般情况下，为了得到上述的多标记分类器Yi，学习系统将学习得到某个实值函数g：X×Y→R。对于训练样本xi及其对应的标记集Yi，g（·，·）在属于Yi的标记上输出较大的值，而在不属于Yi的标记上输出较小的值，即y1∈Y 以及y2∉Yi有g（xi，y1）＞g（xi，y2）。

多标记学习一般采用的评价指标［10］有汉明损失、1－错误率、覆盖率、排序损失及平均精度。

1.2 问题转换

多标记学习主要的解决途径有问题转化法和算法适应法。

问题转换法是通过对多标记训练样本进行处理，将多标记学习问题转换为其他已知的学习问题（如传统的单标记学习问题）进行求解。

算法适应法是通过改进传统的监督学习算法，使其能用于多标记数据的学习；代表性的算法有 ML－KNN和Rank－SVM。

入侵检测可看作二分类问题，即正常记录和异常记录。本文结合以上2种方法，将ML－KNN算法应用于入侵检测，并将入侵数据集中记录分为正常和异常，即多个独立的二分类问题，以构造多标记学习系统，提高入侵检测性能。

2 半监督学习

半监督学习的基本思想为：假定一个存在一个未知分布的有标记数据集L＝｛（x1，y1），（x2，y2），…，（xl，yl）｝和一个未标记数据集U＝｛x1′，x2′，…，xu′｝，期望通过学习函数f′：X→Y 准确地对x预测标记y。

半监督学习［11］是机器学习的一种特殊形式。监督学习需要对大量有标记的数据进行训练，但通常标记数据很难获得，而非标记数据获取相对容易，却难于使用。半监督学习通过标记数据与非标记数据的联合使用来解决上述问题，并建立更好的学习方式［12］。本文结合半监督学习，根据数据固有的性质，既不丢失含标签数据的信息，又能利用非标签数据的信息进行学习，结合 MLKNN算法，提高少部分标记数据的利用效率，以提高分类的精度。

3 基于ML－KNN 的入侵检测算法

3.1 基于多标记学习的KNN算法

ML－KNN算法［9，13］是多标记学习应用于文档和图像领域中最成熟的算法之一，是对已有k近邻算法的改进。该算法的基本思想是采用“k近邻”分类准则，统计近邻样本的类别标记信息，通过最大化后验概率（maximum a posterior，MAP）的方式推理未标记数据的所属集合［10］。

给定样本x及其对应的标记集合y⊆Y，假定算法共取k个近邻。令yx为对应样本x的标记向量，对于其中分量yx（s）（x∈Y），当x为s时，yx（s）＝1，否则yx（s）＝0。设 N（x）表示样本x在训练集中的k个近邻的集合，则样本x的近邻中属于每个标记的数目组成的向量如下：

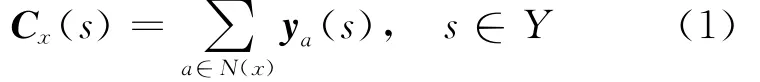
对于每个测试实例t，ML－KNN算法首先确定它在训练集合中的k个近邻组成的集合N（t）。令为实例t中包含标记s的事件，为实例t中不包含标记s的事件，（j∈｛0，1，…，k｝）为在t的k个近邻中有j个包含标记s的事件。基于近邻标记计数向量Ct，测试样本t的预测标记向量yt的计算公式为：

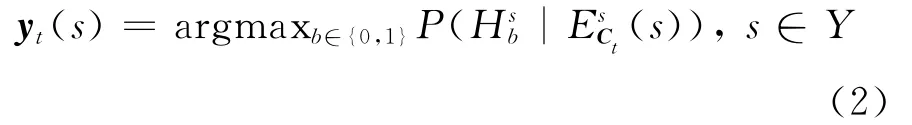
根据贝叶斯规则，（2）式可以改写为：

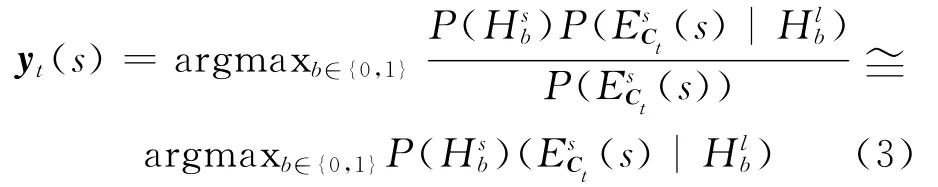
根据（3）式可知，可以直接通过统计计算的方法从训练集合中得到预测标记向量yt、所需的先验概率和后验概率（j∈｛0，1，…，k｝）。算法伪代码如下：

其中，T为训练数据集；k为近邻的数目；t为一个实例；yt为输出的预测标记集合向量；s为一个平滑参数，本文采用Laplace平滑参数，设s＝1。rt为一个实数向量，用来对Y中的标记进行等级划分，rt（l）对应的后验概率为。

3.2 基于ML－KNN 的入侵检测算法

入侵检测可看作二分类问题，因此正常记录标记为（＋1，－1），入侵记录标记为（－1，＋1）。原有的ML－KNN算法是针对多标记学习的，算法中包含了多标记学习评价指标，而本文侧重于入侵检测，因此将算法根据入侵检测评价指标进行部分改进。删除有关多标记学习评价指标的代码，修改主程序 ML－KNN－train 和 ML－KNN－test函数中的代码，增加compare函数来验证入侵检测性能。下面给出算法过程。

输入：训练数据集T，T对应的标记集合T′，测试数据集t，t对应的标记集合t′，近邻数目k，平滑参数s。

输出：测试数据集t的预测标记集合向量yt，后验概率rt（l），入侵检测评价指标（检测率DR和误报率FPR）。

（1）对于∀ti∈t，计算先验概率P（Hlb）。

（2）对每个样例确定k近邻。

（3）计算后验概率P（Elj｜Hlb）。

（4）根据步骤（1）和步骤（3）的结果，结合（3）式得出ti属于正常或异常的可能概率性Outputs，若 Outputs＞ 0.5，则yt（i，j）＝＋1；否则yt（i，j）＝－1。

（5）比较预测标记集合向量yt与标记集合t′，统计总的入侵数目N1、正确检测出的入侵数目N2、总的正常数目M1及将正常记录误判断为入侵 记 录 数 目 （M1－M2），则 DR＝N2／N1，FPR＝（M1－M2）／M1。

4 实验与分析

为了研究多标记学习理论对入侵检测率性能的影响，实验采用了KDD CUP99中的corrected.gz数据集［14］。本实验采用了模式匹配的方式，过滤掉部分入侵类型的攻击。例如，根据land属性的值可判断是否发生了land攻击，land＝1时，可判断该条记录必定为land攻击。但模式匹配只能检测出已知攻击类型，只适合对数据进行前期处理。为了便于处理，实验1按corrected.gz分布比例选取大约1／31的数据，去掉匹配算法检测出来的数据并剔除一些不常见的入侵记录，剩余8 324条作为研究对象来检验本文的入侵检测模型。实验2按照实际网络情况选取代表性数据进行研究分析与对比。

4.1数据预处理

每条数据由41个特征属性和1个决策属性构成。决策属性是每条数据的所属类别，在测试时仅作为判断条件。其余41个属性可分为基本属性集、内容属性集、流量属性集和主机流量属性集。41个属性中有8个属性是离散型变量，剩余为连续型变量。为了使数据符合实验要求，需要对数据进行预处理。

数据的预处理包括符号型数据的数据化处理和数值数据的标准化处理2个步骤。由于每条数据含有3个符号型属性，实验时应将其转化为数值属性，3个符号型属性分别为protocol－type、service、flag。protocol－type属性含有tcp、udp、icmp 3个属性，分别数值化为1、2、3。对于service属性，由于其含有65种取值，若按照之前方法进行处理，虽然解决了数据的数值化问题，但将数据扩大到高维空间中，同时加大了计算量。通过分析，将service类型进行约简，并分成9种取值，分别为 http：1；private：2；urp－i：3；smtp：4；ftpdata：5；ecr－i：6；domain－u：7；other：8；others：9。flag属性含有11种属性，约简成sf：1；rej：2；so：3；others：4。

原始数据记录经过上述处理后，所有属性均变为数值，但仍存在问题。对于连续型的属性特征，不同的属性特征有不同的度量标准，会产生大数吃小数的问题。数据的某些属性特征将被掩盖。为了解决该问题，必须将数据的特征属性值进行标准化，进行如下变换［12］：

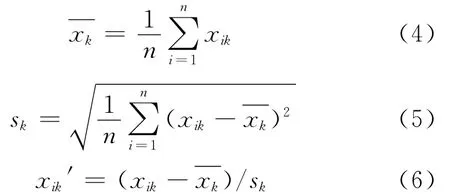
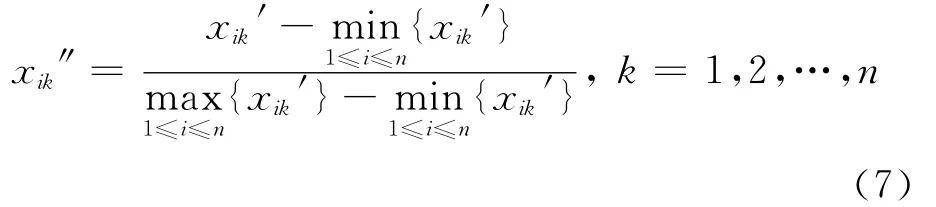
为了方便对数据进行操作，实验时把所有数据放到excel表格中，使用xlsread命令导入Matlab中，此时数据经过数值化并归一化后可以直接用于测试。

4.2 检测结果和算法比较分析

入侵记录主要分为4种：① 扫描与探查（probe）；② 拒绝服务（dos）；③ 对本地超级用户的非法访问（U2R）；④ 未经授权的远程访问（R2L）。本文将normal标记为（1，－1）；probe、dos、U2R和R2L标记为（－1，1），数据的类别分布见表1所列。一个好的入侵检测方案具有高检测率和低误报率的特点，因此，本文用检测率（detection rate，DR）和误报率（false positive rate，FPR）来衡量入侵检测性能。

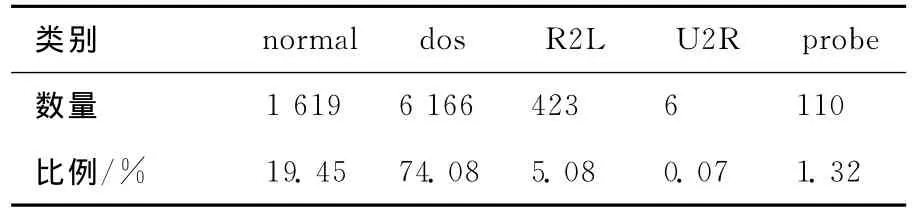
表1 数据的类别分布

利用半监督学习需要提供少量标记数据，实验1设计了3个数据集。3个数据集含有相同的数据，但是标记数据所占的比例不同。其中，数据集1的标记数据约占总数据的1／4；数据集2的标记数据约占总数据的1／3；数据集3的标记数据约占总数据的1／2。取不同K值，分别运行10次，其检测率均为100%，数据集1的误报率均为0.08%，数据集2的误报率均为0.09%；数据集3的误报率均为0.12%。上述数据表明，ML－KNN算法在标记数据的训练下建立了一个较好的模型，误报率基本可以忽略不计。因此，本文提出的方案可以很好地改善入侵检测性能。

在实际的网络运行中，正常数据占大多数，而攻击是少量的，实验2把异常数据记录控制在5%以内。为了与文献 ［3］作比较，实验选取dos的攻击为neptune、smurf；R2L的攻击为guesspasswd；U2R 的攻击为land－module、buffer－overflow、rootkit；probe的攻击为portsweep，并新增portsweep、satan、back、teardrop 入 侵 记 录。本文共做了3组实验测试算法的性能，3组实验选取了不同的数据集对算法进行了测试，其中数据类型及分布见表2所列。

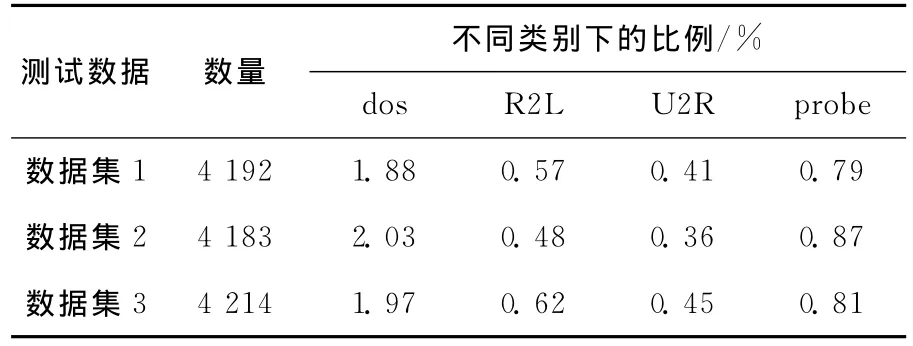
表2 实验测试数据比例

利用半监督学习理论，3个测试数据集部分标记（比例控制在30%～40%），取不同的K值，分别运行10次，实验结果见表3所列。以入侵检测的误报率和检测率作为衡量标准，尽量选择高

检测率和低误报率下的实验数据。经权衡比较，本实验结果见表4所列。

表3 不同K值下的实验2ML－KNN算法分类准确率 %

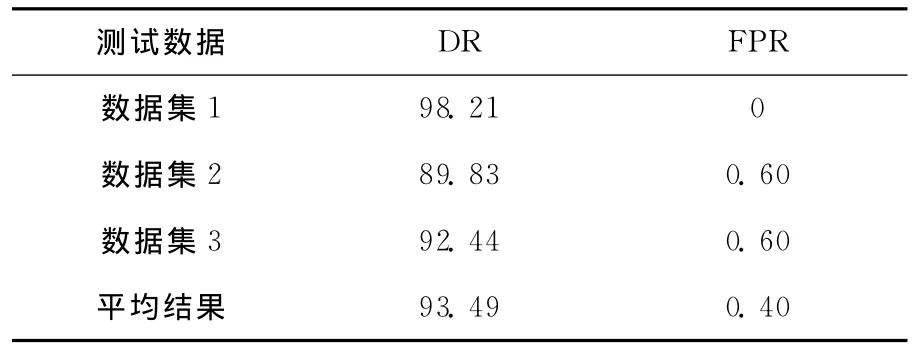
表4 测试结果 %

不同方案的检测率和误报率见表5所列。

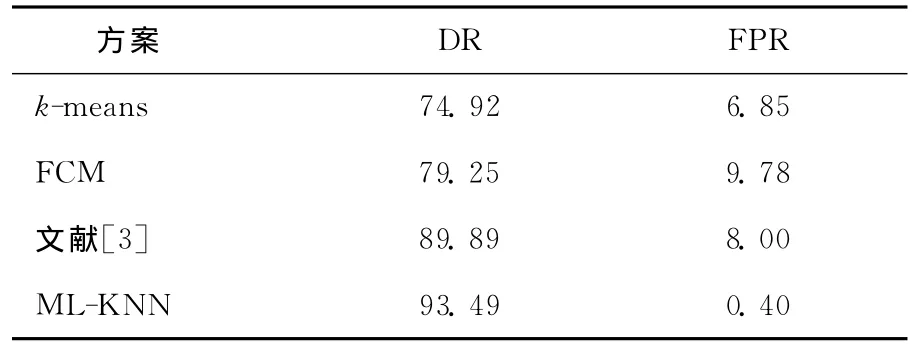
表5 入侵检测性能比较 %

由表5可知，本文算法在保证检测率的同时，有效地降低了入侵检测系统的误报率与k－means硬聚类算法、模糊C均值（fuzzy C－means，FCM）及文献 ［3］相比，本文方法的检测率有了较大的提高，误报率很低，基本可以忽略不计，一定程度上解决了目前入侵检测存在的一些问题。但是该模型纯粹采用KNN技术，在一些情况下是可行的，但是对于已知的标记数据和未标记数据，没有区别哪能个更重要。

5 结束语

实验证明本文提出的ML－KNN算法在入侵检测方面是可行和有效的，优于传统的入侵检测算法。基于 ML－KNN的入侵检测算法将KNN算法和贝叶斯理论相结合，构造学习分类器，从而对KDD CUP99数据集进行有效的分类。基于多标记学习的算法有很多，将其应用于入侵检测系统中进行性能分析以及对海量数据进行分析等将是今后研究的重点。

［1］ 罗守山.入侵检测［M］.北京：北京邮电大学出版社，2003：1－10.

［2］ 黄 越，臧 洌.基于混合分类模型的入侵检测技术研究［D］.南京：南京航空航天大学，2012.

［3］ 张 杰，李永忠.云模型半监督聚类动态加权的入侵检测方法［J］.昆明理工大学学报：自然科学版，2013，38（4），44－47，59.

［4］ 尹才荣，叶 震，单国华，等.基于混合入侵检测技术的网络入侵检测方法［J］.合肥工业大学学报：自然科学版，2009，32（1）：69－72.

［5］ Schapire R E，Singer Y.Boostexter：a boosting－based system for text categorization［J］.Machine Learning，2000，39（2／3）：135－168.

［6］ 宋相法，焦李成.基于稀疏编码和集成学习的多示例多标记图像分类方法［J］.电子与信息学报，2013，35（3）：622－626.

［7］ 陈晓峰，王士同，曹苏群.半监督多标记学习的基因功能分析［J］.智能系统学报，2008，3（1）：83－90.

［8］ 周志华，张敏灵.MIML：多示例多标记学习［J］.机器学习及其应用，2009，3（2）：218－234.

［9］ Zhang Minling，Zhou Zhihua.A lazy learning approach to multi－label learning［J］.Pattern Recognition，2007，40（7）：2038－2048.

［10］ 周志华，杨 强.机器学习及其应用 ［M］.北京：清华大学出版社，2011：179－199.

［11］ Zhu Xiaojin.Semi－supervised learning literature survey［D］.Madison：University of Wisconsin，2006.

［12］ 谢中华.Matlab统计分析与应用：40个案例分析［M］.北京：北京航空航天大学出版社，2010：321－326.

［13］ 郭跃健.多值属性和多标记数据分类［D］.长沙：中南大学，2010.

［14］ KDD Cup 1999Data［EB／OL］.（1999－10－28）［2014－05－23］.http：／／kdd.ics.uci.edu／databases／kddcup99／kddcup99.html.