基于GARCH－EVT模型的证券投资基金动态风险测度

许启发， 陈士俊， 蒋翠侠

（1.合肥工业大学 管理学院，安徽 合肥 230009；2.合肥工业大学 过程优化与智能决策教育部重点实验室，安徽 合肥 230009）

0 引 言

证券投资基金是一种间接的证券投资方式，基金管理公司通过基金发行单位，集中投资者的资金，从事金融工具的投资，以实现共担风险、分享收益。证券投资基金的市场风险分为系统性风险和非系统性风险。无疑，证券投资基金风险的准确预测，对于指导机构投资者、个人投资者进行金融风险防范与风险分担，具有重要的决策参考价值。

当前，VaR风险测度是金融机构度量风险的标准方法，它度量了在一定持有期内以及给定的置信水平下金融资产所遭受的最大可能损失，即

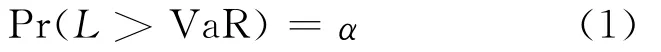
其中，L为金融资产在持有期内的损失；VaR为置信水平1－α下处于风险中的价值。文献［1］运用GARCH模型来研究收益率在尖峰厚尾分布下的VaR值，实证结果表明，在衡量石油风险方面GED分布下的模型要比t分布下的模型更优。文献［2］基于GARCH－时变Copula模型测度社保基金投资组合的动态风险，实证结果表明时变Copula模型的预测结果优于非时变模型。

虽然VaR风险测度概念得到了广泛应用，但VaR不满足次可加性等要求，不是一致性风险度量指标。为弥补这些缺陷，文献［3］提出了ES的概念，ES度量的是损失超过VaR水平的条件期望值，即

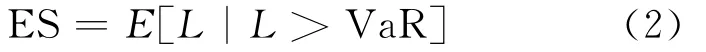
其中，L为金融资产的损失；ES为损失超过VaR的均值。ES是在VaR概念基础上衍生出来的风险度量工具，弥补了VaR的缺陷，更接近于投资者的真实心理感受。目前国内对证券投资基金的ES风险测度的研究工作较少，文献［4］以26只封闭式基金为例，将ES和传统的Sharpe比率相结合，构造基于ES的Sharpe比率来评价基金业绩，研究结果表明，在风险描述方面，基于ES的Sharpe比率比传统的Sharpe比率更加合理。

从上述研究工作来看，通常假设收益率序列服从正态分布，研究方法基本采用GARCH模型，得到静态的VaR估计和ES估计。而实际上金融资产的收益率序列具有尖峰厚尾、波动率聚集和时变等特征，并不服从正态分布，而且VaR风险测度只和收益率分布的尾部有关。文献［5］提出了GARCH－EVT模型，先对原始数据拟合GARCH模型得到残差，然后再对残差序列使用极值理论（EVT）进行建模，很好地解决了动态风险测度中的尾部特征刻画，能够取得比较好的实证效果。迄今为止，GARCH－EVT模型只对国外股票市场的动态VaR进行了测度，如文献［6］将GARCH－EVT模型应用于澳洲综合指数和标准普尔指数的VaR风险测度，结果表明GARCHEVT模型的VaR测度比GARCH（1，1）模型和RiskMetrics模型的结果更准确。基于此，本文将GARCH－EVT模型应用于中国证券投资基金动态风险测度分析，进行如下2个方面的研究：①考虑了一类极值风险特征更为明显的金融资产，即证券投资基金，其具有更高偏度与更高峰度，其收益序列的动态风险特征也更难计量，扩展了先前的应用领域；② 通过似然比检验与Bootstrap方法进行了返回测试，综合比较了Risk－Metrics、GARCH 和 GARCH－EVT 3类模型的动态风险测度效果，结果表明GARCH－EVT模型能够更加准确地描述尾部风险，更适合于证券投资基金的动态风险测度。

1 模型和方法

1.1 动态风险测度方法

1.1.1 基于RiskMetrics模型的动态风险测度

（1）RiskMetrics模型。文献［7］推出风险测度的计量方法（RiskMetrics），并应用到VaR风险测度中。RiskMetrics模型可以表示为：

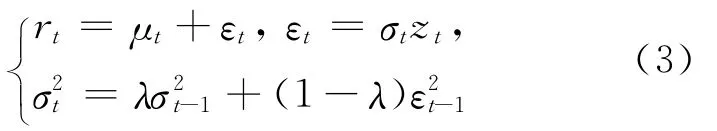
其中，rt为金融资产收益率序列；μt为收益率序列的均值；σt为波动率；εt为随机扰动项；zt为残差序列，假定它服从标准正态分布。实证中，λ为权重参数，在估计日收益序列波动时，RiskMetrics推荐选λ＝0.94。

（2）动态风险测度。记Ft表示第t天可以得到的信息集合，则风险度量制假定rt＋1｜Ft～

由此可以进一步得到原始收益序列t＋1天的动态风险测度为：

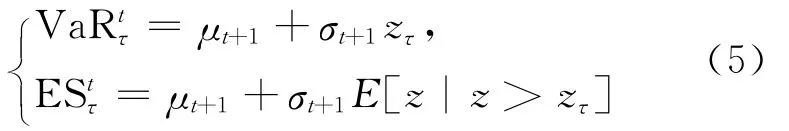
1.1.2 基于GARCH模型的动态风险测度

（1）GARCH模型。文献［8］提出了广义自回归条件异方差模型（GARCH），虽然后来许多学者在GARCH模型的基础上扩展出了IGARCH、EGARCH等衍生模型，但大量的文献研究表明，GARCH（1，1）模型已能够对绝大多数金融时间序列进行很好的描述。GARCH（1，1）模型如下：

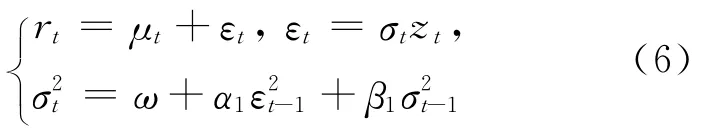
其中，rt为金融资产收益率序列；μt为t时刻的期望收益率；σt为波动率；εt为随机扰动项；zt为残差序列，通常假定它服从标准正态分布；系数ω＞0，α1＞0，β1＞0，以保证条件方差过程的正定性；α1＋β1＜1，以保证条件方差过程的平稳性。

（2）动态风险测度。文献［5］提出动态风险测度时指出，基于正态分布的GARCH（1，1）模型假定收益率序列rt服从正态分布，在第t天运用GARCH（1，1）模型拟合历史数据，通过向前一天预测得到t＋1天的期望收益率μt＋1和波动率σt＋1，则第t＋1天的动态风险测度可以参照（5）式的推导得出，即

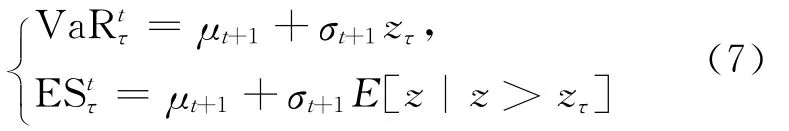
其中，为标准正态分布的τ分位数。

1.1.3 基于GARCH－EVT模型动态风险测度

（1）极值理论的POT方法。极值理论适合对金融时间序列数据的尾部进行建模和预测风险，POT（Peaks－over－Threshold）方法能有效地使用有限的极端观测值，POT方法对超过给定阈值的所有观测值进行建模，用广义帕累托分布（GPD）来拟合这些超出量的分布函数。不妨假设残差序列为z1，z2，…，zt，其分布函数为F（z），给定的阈值为u，超出量的分布函数为：

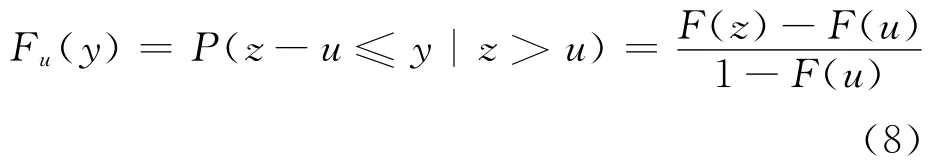
其中，0＜y＜zF－u；zF≤∞为F 的右端点；y＝z－u。

文献［9］提出了对于一个充分大的阈值u，Fu（y）可以由广义帕累托分布近似表示，即

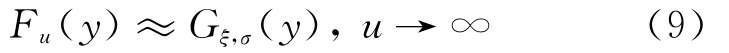
其中，ξ为帕累托分布的形状参数；σ为尺度参数，且有：

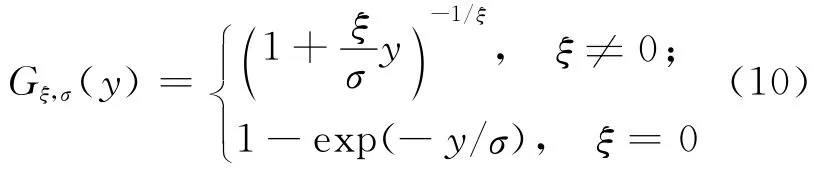
当ξ≥0时，y∈［0，（zF－u）］；ξ＜0时，y∈［0，－（σ／ξ）］。

由（8）式可知，当z≥u时有：

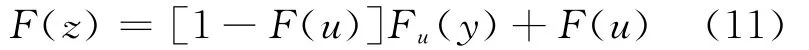
如果n为总观测值的个数，Nu为超过阈值的观测值个数，文献［10］提出用GPD分布替换Fu，用（n－Nu）／n替换F（u），可以得到尾部概率的估计，即

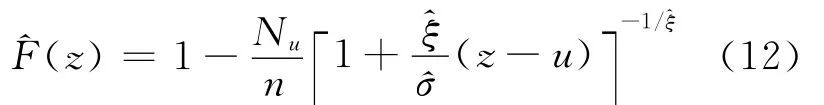
（2）动态风险测度。文献［5］首次提出GARCH－EVT模型，文献［11］将 GARCH－EVT模型运用到股票市场，通过实证研究得到持有期为1d的动态风险测度结果。GARCH－EVT模型分2个步骤：① 运用GARCH（1，1）模型，在第t天通过伪极大似然估计法拟合历史数据，得到残差序列zt，并通过向前一天预测得到t＋1天的期望收益率μt＋1和波动率σt＋1；② 将极值理论POT方法运用到残差序列zt中，估计VaR（z）τ和ES（z）τ。

对于分位数τ≥F（u），由（12）式可以得到残差序列的VaR（z）τ估计为：

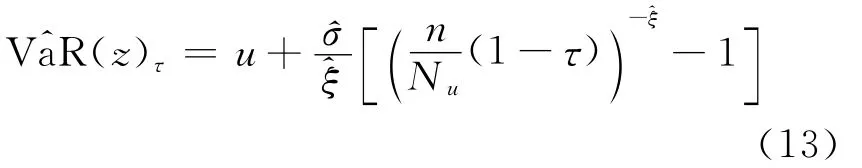
对于ξ＜1可以得到残差序列的ES（z）τ估计为：

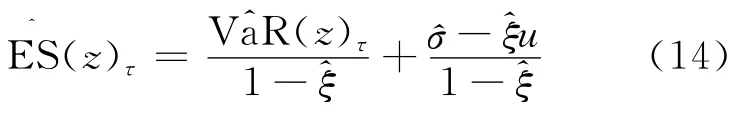
则可以进一步得到原始收益序列t＋1天的动态风险测度，可以参照（5）式的推导得出：

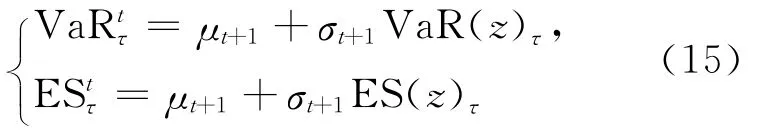
1.2 返回测试

1.2.1 VaR 的返回测试

为了检验模型的有效性，需要对VaR进行返回测试。本文采用的方法是文献［12］提出的似然比检验法。此方法假定VaR估计具有时间独立性，实际损失超过VaR的估计记为失败，实际损失低于VaR的估计记为成功，失败的期望概率为p＊＝α（1－α为置信水平）。假定估计VaR的置信水平为1－α，实际考察天数为T，失败天数为N，则失败频率为p（N／T），这样失败频率就服从一个二项式分布，零假设为H0：p＝p＊，备择假设为H1：p≠p＊。文献［12］提出采用似然比检验法对零假设检验，似然比统计量为：

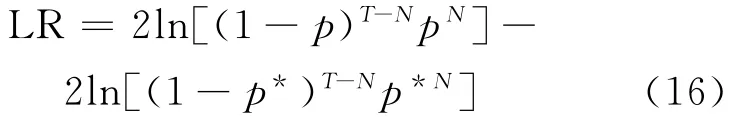
在零假设条件下，统计量LR服从自由度为1的χ2分布。即如果估计的LR值大于自由度为1的χ2分布的临界值，则拒绝零假设；反之则接受零假设。此外还可以通过该检验的P值（P－Value）判断模型的精确程度，如果返回测试的P值越大，则说明越不能拒绝零假设，表明该模型的精确程度越高。

1.2.2 ES的返回测试

文献［13］采用Bootstrap方法对ES进行返回测试。定义如下形式的超出残差：

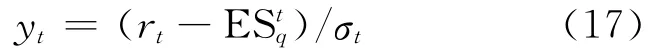
其中，rt为损失超过VaR值的日对数收益率。文献［13－14］指出如果估计ES所使用的模型足够精确的话，超出残差yt应具有零均值，即μy＝0。设该超出残差序列包含I个样本点，则由（18）式产生一个由超出残差序列中每一个样本值yt与其均值的离差所构成的新序列lt（t＝1，2，…，I），并称其为初始样本。lt为：

由初始样本估计以下检验统计量的值为：

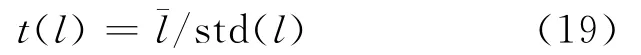
由于yt经常呈现明显的右偏分布，所以检验的备择假设为μy＞0，即该检验为单尾检验，因此估计出｛t1（l），…，tB（l）｝中大于t0（l）的数值所占的比例，这一比例即是用于检验μy＝0的显著性P值，P值越大，越不能拒绝原假设，即认为模型对ES风险测度的估计精度越高。

2 实证研究

2.1 数据选取与统计分析

本文选取2003年1月2日至2012年12月31日的股票基金、混合基金和债券基金（代码分别为H11021、H11022和H11023）的日收盘价数据作为研究对象，共2 428个日收盘价，数据源于锐思金融数据库。日对数收益率的定义为：rt＝100×（lnPt－lnPt－1），其中Pt是第t日的基金收盘价，共2 427个日对数收益率。这一时期包含了2007—2009年这一波动性较强、风险较高时期，存在极值风险。

各基金日对数收益率的描述性统计、JB检验和LM检验结果见表1所列。就收益情况而言，股票基金的平均收益最高，为0.057；其次为混合基金，最低为债券基金。不过，股票基金收益的方差也最大，为1.915；其次为混合基金，最低为债券基金。上述结果表明股票基金平均收益最高，风险最大，而债券基金平均收益最低，风险却最小。这一结果完全符合金融市场的“高风险－高收益”特征。

表1中的偏度都小于0，超额峰度都大于0，偏度与超额峰度统计结果表明，3只基金的收益序列都呈现左偏特征，并且都是尖峰厚尾的，不符合正态分布的特征，这一结果由J－B检验得到了加强；LM检验结果表明序列有明显ARCH效应。

表1 各基金日对数收益率的描述性统计、J－B检验和LM检验

2.2 动态风险测度

2.2.1 基于RiskMetrics模型动态风险测度

采用RiskMetrics模型估计动态风险测度时，首先要根据（3）式估计出每一天的波动率，由于第1天无法估计，因此得到2 426个波动率，然后在95%和99%置信水平下通过（5）式得到2 426个动态VaR和ES的预测值。具体的估计结果及图略。

2.2.2 基于GARCH模型的动态风险测度

由上述分析结果可知，各基金的日对数收益率序列都是尖峰厚尾的，此外存在很明显的ARCH效应，因此采用GARCH（1，1）模型在移动窗口中拟合历史数据。本文使用1 000个日对数收益率（约4a的数据）作为移动窗口，假定对数收益率序列服从标准正态分布，在95%和99%置信水平下通过（7）式得到1 427个动态VaR和ES的预测值。具体的估计结果及图略。

2.2.3 基于GARCH－EVT模型动态风险测度

该风险测度可以分4个步骤来完成：① 使用上述GARCH模型估计结果，得到残差序列；② 分别以5%和1%的分位数作为阈值，对残差序列拟合成广义帕累托分布（GPD）；③ 根据（13）式、（14）式给出残差序列的VaR和ES的估计；④将残差序列的VaR和ES的估计结果代入（15）式，最终得到在95%和99%置信水平下1 427个动态VaR和ES风险测度。

95%和99%置信水平下GARCH－EVT模型估计的各基金的动态VaR和ES的比较如图1、图2所示。图中VaR由虚线表示，ES由实线表示。

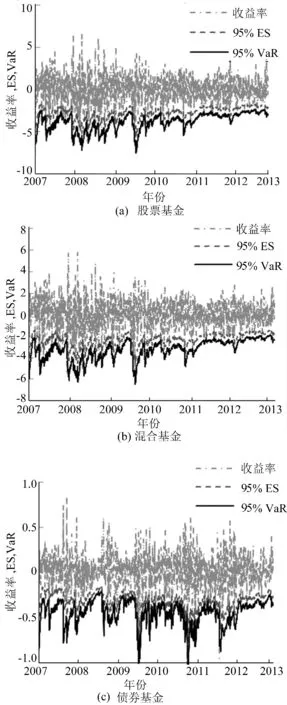
图1 GARCH－EVT模型估计的95%置信水平下动态VaR和ES的比较

由图1、图2可以看出：①各基金的收益率序列有明显的波动率聚集效应；② 各基金的ES总是大于VaR，表明ES风险测度比VaR风险测度更加保守；③ 股票基金和混合基金的VaR和ES明显大于债券基金的VaR和ES，表明股票基金和混合基金的风险比债券基金大，这也符合债券基金“低风险－低收益”的特征；④ 各基金的VaR和ES基本位于收益率序列的下方，初步表明基于GARCH－EVT模型的动态VaR和ES风险测度结果较为准确。

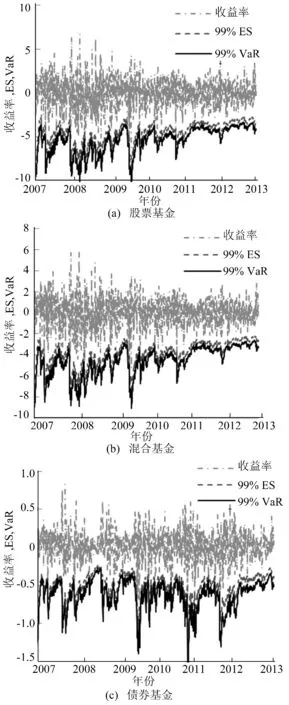
图2 GARCH－EVT模型估计的99%置信水平下动态VaR和ES的比较

2.3 返回测试

2.3.1 VaR的返回测试

为了检验模型的有效性，可以将持有期为1d的动态V

aR测度和第2天的实际损失进行比较。如果实际损失超过了动态VaR测度，就称出现了1次失败，从而估计出动态VaR测度的失败比率。如果实际失败比率大于理论失败比率，那么表明低估了风险，反之则高估了风险，只有与理论水平相当才能说明模型是可靠的。表2所列为相应置信水平下、相同时间段内基于RiskMetrics模型、GARCH模型和GARCH－EVT模型得到的动态VaR测度的返回测试结果，主要包括：失败比率、似然比检验的P值。从表2可以看出2点结论。

（1）股票基金和混合基金的VaR风险测度的返回测试结果表明：RiskMetrics模型估计的VaR风险测度都低估了风险；GARCH模型在95%置信水平下给出了较为准确的风险测度结果，但在99%置信水平下低估了风险；GARCHEVT模型估计的VaR风险测度的实际失败比率全都小于理论失败比率，并且都接受了返回测试的零假设，给出了较为准确的风险测度结果。

（2）债券基金的VaR风险测度的返回测试结果表明：3种模型估计的债券基金的VaR风险测度都高估了风险，并在95%置信水平下拒绝接受返回测试的零假设。

这一结果表明，3种模型都较为保守，倾向于高估风险。

综合表2的分析结果可知，GARCH－EVT模型能提供比GARCH模型和RiskMetrics模型更为准确的动态VaR风险测度结果。

2.3.2 ES的返回测试

从图1、图2可以看出，ES总是大于VaR，说明ES风险测度比VaR风险测度更保守，能更适应于描述极值事件的发生，准确测度极端风险。鉴于VaR风险测度低估了极端金融风险，需要使用ES风险测度作为补充。本文采用Bootstrap方法（令B＝1 000），对动态ES风险测度效果进行了返回测试，结果见表3所列。

表3中的数字为Bootstrap检验的P值，可以看出，在95%、99%2个置信水平下，GARCHEVT模型都取得了最大的P值，即GARCHEVT模型的估计精度最高，能提供比GARCH模型和RiskMetrics模型更为准确的动态ES风险测度结果。

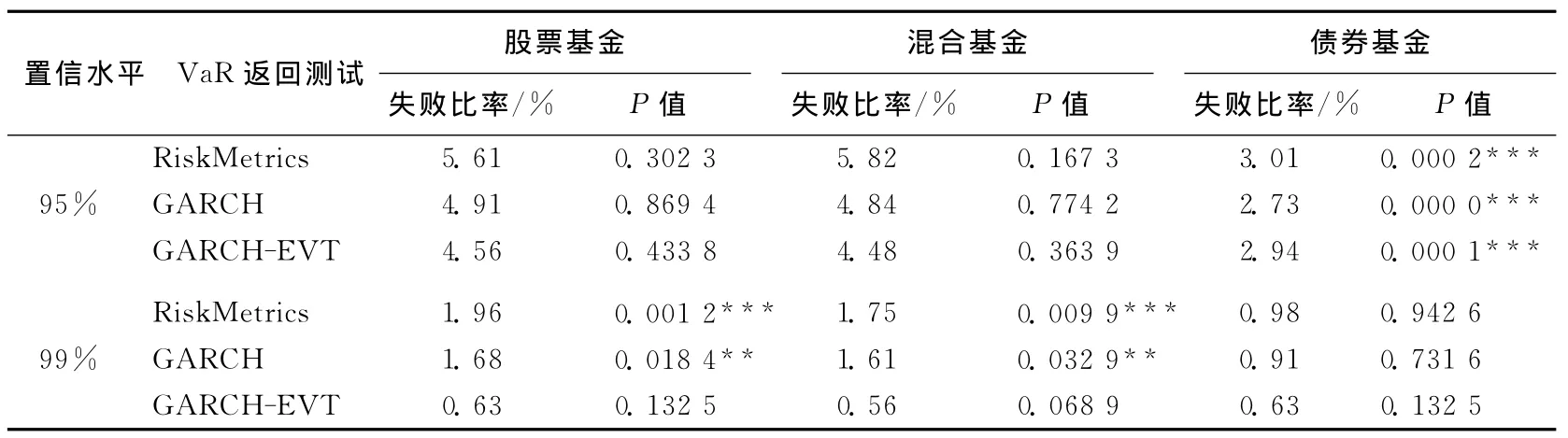
表2 动态VaR风险测度的返回测试结果

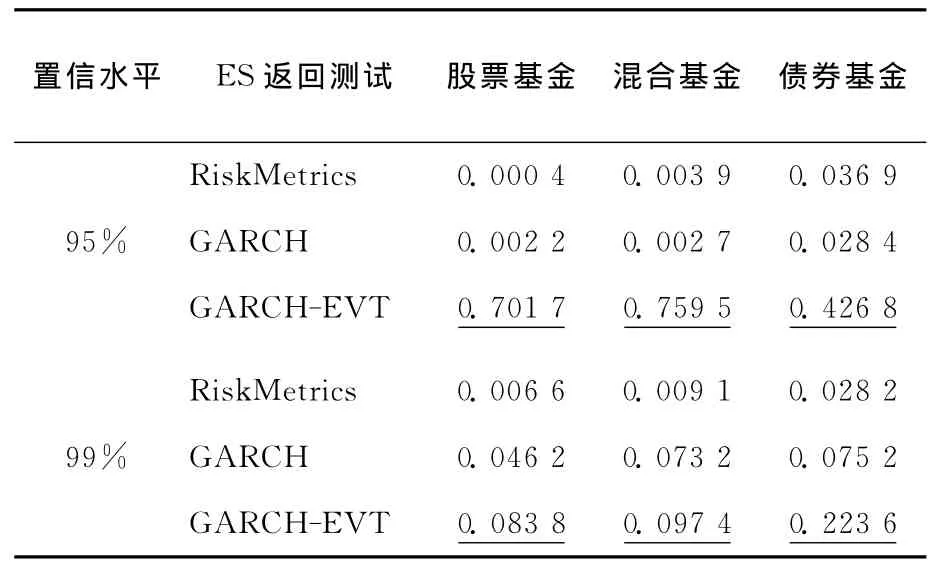
表3 动态ES风险测度的返回测试结果

3 结论与展望

本文主要扩展了GARCH－EVT模型应用领域，考虑了证券投资基金收益的动态风险测度问题，该金融资产收益比股票收益或债券收益具有更高偏度与峰度，具有明显的极值风险特征。以中国股票基金、混合基金和债券基金为研究对象，实证比较了RiskMetrics模型、GARCH模型和GARCH－EVT模型对我国证券投资基金市场的动态风险测度效果。

实证结果表明：① 基于GARCH－EVT模型给出的各类基金动态VaR和ES风险测度结果更为准确，特别适合于极端风险测度；②ES风险测度比VaR风险测度更加保守，在风险较高的时期，应采用GARCH－EVT模型估计的ES风险测度作为VaR风险测度的补充。

在本文基础上，可以从3个方面开展更为深入的研究工作：①考虑GARCH族的其他模型与极值理论方法相结合，给出新的动态金融风险测度方法；② 在持有期为1期（天）的动态风险测度的基础上，考虑持有期为多期（天）的情况；③ 依据证券投资基金的其他分类展开研究工作，如研究开放式基金、封闭式基金等的动态风险测度问题，检验不同类型的证券投资基金动态风险特征。

［1］ 伍笑萍，李忠民.基于GARCH模型的 WTI原油现货市场的风险分析［J］.合肥工业大学学报：自然科学版，2013，36（9）：1127－1131.

［2］ 李超杰，江红莉.基于动态Copula的社保基金投资风险测度［J］.统计与决策，2011，（23）：147－150.

［3］ Artzner P，Delbaen F，Eber J M，et al.Coherent measures of risk［J］.Mathematical Finance，1999，9（3）：203－228.

［4］ 刘沛欣，田 军，周 勇.基于VaR和ES调整的Sharpe比率及在基金评价中的实证研究［J］.数理统计与管理，2012，31（4）：735－750.

［5］ McNeil A J，Frey R.Estimation of tail－related risk measures for heteroscedastic financial time series：an extreme value approach［J］.Journal of Empirical Finance，2000，7（3）：271－300.

［6］ Singh A K，Allen D E，Robert P J.Extreme market risk and extreme value theory［J］.Mathematics and Computers in Simulation，2013，94：310－328.

［7］ Morgan J P.Introduction to RiskMetrics［R］.New York：JP Morgan，1994.

［8］Bollerslev T.Generalized autoregressive conditional heteroskedasticity［J］.Journal of Econometrics，1986，31（3）：307－327.

［9］ Pickands III J.Statistical inference using extreme order sta

tistics［J］.The Annals of Statistics，1975，3（1）：119－131.

［10］ Smith R L.Estimating tails of probability distributions［J］.The Annals of Statistics，1987，15（3）：1174－1207.

［11］ Allen D E，Singh A K，Powell R J.EVT and tail－risk modelling：evidence from market indices and volatility series［J］.The North American Journal of Economics and Finance，2013，26：355－369.

［12］ Kupiec P H.Techniques for verifying the accuracy of risk measurement models ［J］.The Journal of Derivatives，1995，3（2）：75－84.

［13］ Taylor J W.Estimating value at risk and expected shortfall using expectiles［J］.Journal of Financial Econometrics，2008，6（2）：231－252.

［14］ 王 鹏， 魏 宇.基于多分形波动率测度的ES风险度量［J］.系统管理学报，2012，21（2）：192－200.