短裤特征截面曲线的径向基函数神经网络模型构建
叶晓露,庞程方,金娟凤,邹奉元,2
(1.浙江理工大学服装学院,浙江 杭州 310018;2.浙江理工大学浙江省服装工程技术研究中心,浙江 杭州 310018)
短裤特征截面曲线的径向基函数神经网络模型构建
叶晓露1,庞程方1,金娟凤1,邹奉元1,2
(1.浙江理工大学服装学院,浙江 杭州 310018;2.浙江理工大学浙江省服装工程技术研究中心,浙江 杭州 310018)
将着装人台进行三维扫描获取点云数据,截取与人体特征部位相对应的短裤特征截面。将原数据坐标点转化为极坐标系下的极角与极径值后,以极角值作为输入向量,极径值作为输出向量,构建短裤特征截面曲线的径向基函数(RBF)神经网络模型,并与反向传播(BP)神经网络、最小二乘法及三次样条函数的拟合效果进行比较。结果表明:神经网络拟合曲线的平均绝对误差比最小二乘法及三次样条函数方法小,仿真输出曲线和原始数据非常接近,且曲线光滑;RBF网络的训练速度更快,所需训练步数少,拟合效率明显优于BP神经网络。
短裤;特征截面;RBF神经网络;曲线拟合;MatLab仿真
服装特征截面曲线是服装穿于人体后在人体特征部位截取的三维形状。Machiko Miyoshi等[1]运用三维测量系统获取着装截面并由此建立服装样板设计系统。Susan Ashdown等[2]对合体裤装横截面进行分析,量化了服装和人体间的关系。
由于着装人体各高度上的截面形状凹凸起伏,服装截面曲线的拟合具有复杂性。徐继红等[3]用最小二乘法三次多项式插值建立人体和服装曲线拟合算法,发现将5点作为1段进行三次多项式拟合效果较好。郑娟[4]将原始坐标转化为极坐标后采用最小二乘法对人体截面进行拟合,但随着拟合阶数的增大,拟合曲线出现振荡,对于非线性函数多项式拟合效果不是很理想[5]。在曲线拟合的研究中样条曲线拟合也是较为传统和常用的方法。Taya[6]在服装合体性研究中用五阶样条函数对横截面上的极坐标点进行拟合。Wang[7]采用三次样条函数拟合着装与未着装人体胸围、腰围和臀围3个截面的曲线。盛仲飚等[5]在三次样条曲线拟合中发现样条拟合涉及矩阵求逆,拟合点数增加矩阵将增大,使得求逆越麻烦[8]。而人工神经网络能够模仿动物的神经网络行为特征,将神经网络应用于曲线拟合,把采集的离散数据通过训练得到模型模拟相应的非线性系统从而得到较好的逼近函数[9],同时避开了矩阵求逆的繁琐。径向基函数(RBF)神经网络与BP神经网络在曲线拟合中是较常用的2种人工神经网络模型。
本文将人工神经网络引入到服装特征截面曲线拟合中进行尝试。以下装短裤各特征截面为例,首先将三维扫描得到的下装特征截面点云原始坐标点转化为极坐标点,构建RBF神经网络模型将离散极坐标数据点进行训练并拟合得到连续的极坐标曲线。并与BP神经网络、最小二乘法及三次样条函数的拟合效果进行对比,为提高服装特征截面及人体截面曲线拟合精度,有效展现服装截面三维波形形态提供依据。
1 数据获取
人体的横截面可以清楚反映出人体凸点的三维特征和位置。裤装的特征横截面包括腰、腹、臀、裆、裤口等截面,在这些截面处有其各自特点并具有复杂性。本文对短裤中不同的特征截面进行曲线拟合,根据不同截面的仿真效果对RBF神经网络算法的性能进行评估。
本文选用常用面料白坯布,根据图1中的典型女西短裤款式制作实验样裤,运用三维扫描仪对着装人体进行扫描,以获取短裤着装后的真实形态,扫描所得数据以*.wrl格式储存。将文件导入3DMax去除手臂以及腰部以上的躯干部位。用获取截面功能分别得到图像的腰围、腹围、臀围、裆围以及裤口5个人体下半身服装特征部位的截面,截面选取位置如图1所示。将截面点云数据同样以*.wrl格式储存,用MatLab读取各个截面的坐标点数据。

图1 服装特征截面部位Fig.1 Typical cross section
由于TC2三维扫描仪所得的多面网格数据以三维坐标(x,y,z)的形式储存,取同一z坐标则得到散点坐标(x,y),而服装特征截面为一闭合曲线,闭合曲线中一个x值无法对应唯一的y值,因此将原数据坐标用MatLab中cart2pol函数转化为极坐标系下的(θ,ρ),使得坐标点中极角与极径一一对应,如图2所示。

图2 极坐标转化图Fig.2 Polar conversion chart
2 RBF神经网络方法
RBF网络是一种3层前向网络,基于RBF的曲线拟合方法将低维的模式输入数据转换到高维空间中,使得低维空间内的线性不可分问题在高维空间内变得线性可分。RBF网络与BP网络的学习过程类似,二者的主要区别为使用的作用函数不同。BP神经网络隐层使用的是Sigmoid函数,是一种全局逼近的神经网络;而RBF网络中的作用函数是高斯基函数,是局部逼近的神经网络[10-11]。
将极坐标数据θ作为输入向量,ρ作为输出向量,拟建立单输入单输出的RBF神经网络模型。其中,网络的输入层到隐含层实现x→Fi(x)的非线性映射,隐含层节点的作用函数为高斯基函数;隐含层到输出层实现Fi(x)→yk的线性映射。
当网络输入训练样本x=[x1x2… xn]T时,输出层第k个神经元网络输出表达式为

隐含层节点的作用函数为高斯基函数时,隐含层第i个神经元的输出表达式为

RBF网络的训练过程为由实验样本确定训练的隐含层与输出层之间的权值ω,最终权值[12]为

式中:x为输入向量;yk为输出层第k个节点的输出;Fi(x)为第i个隐含层节点输出;σi为第i个隐节点的标准化常数;ci为第i个隐节点高斯函数的中心向量;ωik是隐含层到输出层的加权系数。
3 模型的构建与训练
对于3层RBF神经网络,为实现模型的训练,首先将原始坐标转化为极坐标后利用已有数据点中的极角值以及与之对应的极径值对神经网络进行离线训练,使神经网络通过权值记忆极角与极径之间存在的对应关系。再由得到的神经网络将截面曲线上每隔0.01度所取的数据点作为自变量加到神经网络的输入端,相应地得到该点所对应的极径,取值范围为0~2π(1-1/N),其中N=36000为常数。因此,最终求算仿真精度为0.01度的数据点,完成拟合工作。因此,运用RBF神经网络进行截面曲线拟合时,根据模型训练所得的对应关系,由极坐标数据θ预测ρ是在一定意义下最佳地接近已知数据的过程。预测所得的l与实际值偏差越小,由该数据点对拟合所得到的截面曲线将越接近服装真实的截面形态。着装后的裤装尤其是裆部上的形态存在不易观察的难点,对于裤装特征截面的准确获得将为短裤着装形态的研究奠定一定的基础。
在进行模型训练的时候,为了加快训练的收敛速度需要对式(2)中的各代表量进行相应处理。归一化x和ci,分别记做P和IW,将1/σ替换为b1在程序中进行储存。对于归一化后样本进行训练时需要注意的是,将原坐标系下的数据转化为极坐标系下的点时,0与2π位置的点值在拟合时可能会出现相差较大的情况,从而导致首尾相接的接口处没有闭合,因此,取极坐标点头部和尾部的数据分别再复制于尾部和头部。实验中发现各取20个数据时拟合效果已较好且不影响拟合速度,因此,数据点将扩大至小于0到大于2π的范围,因此将首尾多取的数据点中的最大值和最小值一同进行归一化处理。
进行数据处理后利用MatLab环境下的函数di(x)替换式(2),gi(x)替换式(1)得到:

式中:radbas表示高斯函数;purelin表示线性函数。
图3示出RBF神经网络采用MatLab实现的网络结构图。图中:R为输入数;S1为第1层神经元数;S2为第2层神经元数;a1为径向基函数输出;a2为纯线形输出;IW为隐含层的权值(即中心向量);LW2为输出层权值;b1为隐含层的阈值;b2为输出层的阈值;dist为距离函数,其运算规则为

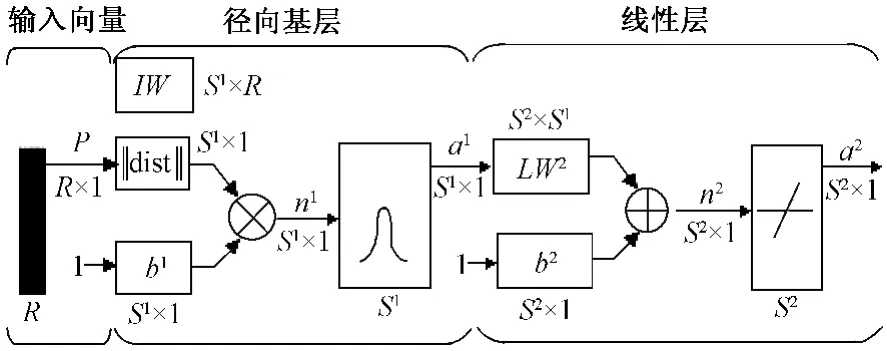
图3 MatLab实现的网络结构Fig.3 Structure of RBF using MatLab
本文在MatLab神经网络工具箱中创建RBF网络设计函数newrb,自动选择隐层节点数使得误差为10-4,步骤如下:
1)用所有输入样本即极坐标下的坐标点对网络进行仿真训练。
2)寻找误差最大的输入样本Pi。
3)增加一个径向基神经元。spread为径向基函数的扩展系数(分布密度),其要根据实际情况进行选择,默认值为1。本文由经验公式将spread值设为240/R*0.04,R为训练样本个数。
4)把径向基神经元的输出a1作为线性网络层的输入,从而重新设计线性网络层使得误差达到最小。
5)当输出误差均方误差达到目标误差,或神经元数目达到规定的上限值完成训练,否则重复上述步骤。
BP神经网络中隐含层选用3层,根据经验公式估计BP网络有10个隐含层节点,其中隐含层神经元的激发函数为logsig,输出层神经元的传递函数为purelin,选用学习率算法是trainlm。BP网络的目标误差同样设为10-4。
另外,最小二乘法拟合中,为了方便比较同样设定误差目标为10-4,拟合阶数从1至一指定最高次数,若拟合过程中某个次数已满足目标误差则完成拟合,若没有达到目标误差则直到指定最高次数,然后选取误差均方最小的次数。三次样条曲线拟合中采用spline函数进行拟合。
4 实验结果与讨论
在短裤各截面所有数据点中选取90%的数据点作为拟合点集,剩下10%作为测试点集,且测试集点按顺序间隔选取保证各方法拟合选取的测试样本相同以计算平均绝对误差。平均绝对误差计算公式为

式中:p1k为测试点拟合所得极径值;p2k为测试点实际极径值。同时进行计时,并分别绘制拟合效果图,拟合结果如表1所示。
由表1结果可见,最小二乘法虽然原理简单易于求解,但其拟合均方误差与其他方法相比较大,均未达到设定的目标误差10-4,测试点的平均绝对误差与2种神经网络拟合方法相比也较大。由图4所示的最小二乘法的拟合效果图可见,截面原数据中有较多数据点偏离拟合曲线,因此最小二乘法在拟合精度要求较高时并不具有很好的效果。

表1 各服装特征截面曲线拟合结果Tab.1 Fitting results of all clothing cross s ection curves

图4 最小二乘拟合结果Fig.4 Fitting results of least square method
三次样条函数在拟合时其拟合曲线经过所有的数据点值,如图5所示,其拟合的均方误差为0,且在数据点较少时拟合速度快,但其测试点的平均绝对误差却较大,说明不能很好地预测拟合给定数据点外的数据点,导致拟合曲线和实际截面曲线存在较大误差。且如图6(a)所示,在拟合如同裆部截面上前后中处时,由于人体在该部位有较明显的凹陷使得服装表面在此处也形成凹陷,由三次样条函数所拟合的曲线为连接每个原数据点在前后中处形成了尖角,曲线并不圆顺。且由三次样条函数涉及矩阵求逆,拟合点数增加时矩阵将增大,使得求逆越麻烦,因此若当扫描所得的数据点很多时,其拟合速度将大大减慢。
由表1可知,采用RBF和BP神经网络进行曲线拟合,其均方误差均达到所设定的目标误差10-4,显然比最小二乘法的拟合精度高。且平均绝对误差与最小二乘法及三次样条的平均绝对误差相比大大减小,但从拟合速度上比较,由于神经网络存在训练过程,因此所需时间相对要长。
比较各截面RBF神经网络与BP神经网络的拟合效果发现,RBF神经网络训练过程中,隐含层的节点个数是从0开始,过程中通过检查输出误差(MSE)与目标误差(goal)的偏差值,使建立的网络自动增加神经元个数,直到网络的输出均方误差MSE符合目标10-4的要求,此时由RBF神经网络训练所需训练步数显然小于由BP神经网络训练所需训练步数。例如着装臀围截面曲线训练的神经元数目增加到144个,即RBF网络在臀围截面中的训练步数为144,如图7所示,而BP神经网络在达到规定的期望均方误差10-4时,臀围截面中的训练步数为402,如图8所示。BP神经网络的训练步数远远大于RBF神经网络。同时比较二者的训练时间发现,运用BP神经网络进行各着装特征截面拟合所用的训练时间为使用RBF神经网络的3~5倍。显然,RBF神经网络相对于BP神经网络的训练速度快,所需的训练步数少,能在较短时间内完成服装特征截面曲线的拟合。
图5 三次样条拟合结果Fig.5 Fitting results of cubic splines

图6 裆部后中处拟合结果Fig.6 Fitting results of back center of crotch.(a)Cubic splines;(b)RBF
对创建好的网络进行仿真,同时绘制得到样本数据的拟合曲线,由RBF和BP神经网络得到的拟合曲线分别如图9、10所示。由图9可见,建立的RBF网络对训练样本进行了很好的拟合,训练网络的仿真输出曲线和原始数据非常接近,拟合曲线整体光滑且无振荡。这说明训练后的网络对服装及人体特征截面此类非线性封闭曲线的逼近效果很好。由图10可见,训练后的BP神经网络对特征截面曲线的拟合效果也同样非常好,仿真输出曲线和原始曲线接近。

图7 RBF误差性能曲线Fig.7 Error performance curve of RBF

图8 BP误差性能曲线Fig.8 Error performance curve of BP
由表1可知,RBF神经网络对着装各截面测试点的平均绝对误差为0.2% ~0.6%,BP神经网络为0.2% ~0.7%,较为接近且均在1%以下,相对于最小二乘法的平均绝对误差1.0%~1.3%以及三次样条的平均绝对误差1.0% ~1.4%显然较小,因此,在拟合效果上2种神经网络的精度均较高。

图9 RBF拟合结果Fig.9 Fitting results of RBF

图10 BP拟合结果Fig.10 Fitting results of BP
对于图6(a)出现的问题,由图6(b)可见RBF拟合曲线在人体凹陷处圆顺无尖角且又与原数据点接近偏差小,该方法对于前后数据点位置起伏较大的拟合较优。由表1可见,对于同一着装截面2种神经网络的平均绝对误差接近。但由RBF神经网络训练的一组截面比BP神经网络训练的一组截面所需的训练时间明显短,速度快。而在达到规定的期望均方误差前提下,RBF网络的训练步数要小于BP神经网络。
由上述分析可知,RBF神经网络拟合服装特征截面曲线具有良好的效果,拟合得到特征截面曲线以后,若要生成完整的裤装,接着在特征部位之间按照一定的步长对扫描所得的着装人体模型进行截取,即可得到一系列的截面环,在后续研究中可通过轮廓线表面重建的方法,根据截面环来构建裤子曲面。
5 结论
1)采用神经网络对特征截面曲线进行拟合,仿真输出曲线和原始数据均非常接近,能够达到目标误差且平均绝对误差小,拟合曲线整体光滑且无振荡,训练后的网络对服装及人体特征截面此类非线性封闭曲线的逼近效果很好。
2)RBF神经网络相对于BP神经网络的训练速度快。在达到规定的期望均方误差前提下,RBF网络的训练步数要少于BP神经网络。
[1] MACHIKO Miyoshi,TAEKO Hirokawa.Study on the method of measuring a vacant space distance in a worn jacket for clothing pattern design[J].Journal of the Japan Research Association for Textile End-Uses,2001,42:233-242.
[2] SUSAN Ashdown,SUZANNE Loker.Use of body scan data to design sizing systems based on target markets[J]. National Textile Center Annual Report,2011(11):1-5.
[3] 徐继红,张文斌,夏明.人体与服装特征曲面间阔体松量分配关系[J].天津工业大学学报,2009,28(5):27-32.XU Jihong,ZHANG Wenbin,XIA Ming.Vacant ease distribution relationship between body and garment[J].Journal of Tianjin Polytechnic University,2009,28(5):27-32.
[4] 郑娟.立体裁剪专用松量模型的研制[D].杭州:浙江理工大学,2010:1-40.ZHENG Juan.Exploitation of special ease model for draping[D].Hangzhou:Zhejiang Sci-Tech University,2010:1-40.
[5] 盛仲飚,同晓荣.BP神经网络在曲线拟合中的应用[J].科学技术与工程,2011,11(28):6998 -7000.SHENG Zhongbiao,TONG Xiaorong.The application of BP meural networks in curve fitting[J].Science Technology and Engineering,2011,11(28):6998 -7000.
[6] YOSHIKO Taya.An evaluation method of clothing fitness with body[J].Proceedings of the Human Factors and Ergonomics Society Annual Meeting,2000,44:762 -765.
[7] WANG Z H.Study on the method of measuring a vacant space distance in a worn jacket for clothing pattern design[D].Hong Kong:The Hong Kong Polytechnic University,2007:1 -56.
[8] 吴长楠.神经网络在曲线拟合中的应用[J].苏州职业大学学报,2000(4):62-65.WU Changnan.Neural network in the application of curve fitting[J].Journal of Suzhou Vocational University,2000(4):62 -65.
[9] 严晓明,郑之.BP与RBF网络在一些非线性曲线拟合上性能的比较[J].福建农林大学学报:自然科学版,2011,40(6):653 -656.YAN Xiaoming,ZHENG Zhi.Performance comparison between some nonlinear curves fitting with BP and RBF[J].Journal of Fujian Agriculture and Forestry University Natural Science Edition,2011,40(6):653 -656.
[10] 李国勇.智能控制及其 MATLAB实现[M].北京:电子工业出版社,2005:31.LI Guoyong.Intelligent Control and MATLAB[M].Bejing:Publishing House of Electronics Industry,2005:31.
[11] 刘金琨.智能控制[M].北京:电子工业出版社,2014:133.LIU Jinkun.Intelligent Control[M].Beijing:Publishing House of Electronics Industry,2014:133.
[12] 彭继慎,董晶.基于RBF神经网络的控制系统传感器故障诊断方法[J].现代电子技术,2009(12):179-182.PENG Jishen,DONG Jing.Method of control system sensor fault dignosis based on RBF neural network[J].Modern Electronics Technique,2009(12):179 -182.
Construction of radial basis function neural network models for typical cross section curve of shorts
YE Xiaolu1,PANG Chengfang1,JIN Juanfeng1,ZOU Fengyuan1,2
(1.School of Fashion Design & Engineering,Zhejiang Sci-Tech University,Hangzhou,Zhejiang 310018,China;2.Zhejiang Provincial Research Center of Clothing Engineering Technology,Hangzhou,Zhejiang 310018,China)
Three-dimensional body scanning technique is used to collect point clouds data from the dressed mannequin and capture the shorts'typical cross section that is correspondent to the feature points of body.By changing the original coordinate point to polar angle and polar radius under the polar coordinate system,and taking the polar angle as the input and the polar radius as the output,RBF neural network model of the shorts'typical cross section is established.Then the curve of clothing typical cross section is fitted and the fitting effect is compared with that of BP,least square method and cubic splines.The experiment results show that the mean average absolute percentage error of both neural networks is less than that of least square method and cubic splines.The simulation output curve is very close to original data and the curve is smooth.RBF network has much higher training speed,fewer training steps,and fitting efficiency superior to the BP neural network.
shorts;typical cross section;RBF neural network;curve fitting;MatLab simulation
TS 941.17
A
10.13475/j.fzxb.20140405006
2014-04-17
2014-11-06
国家国际科技合作专项项目(2011DFB51570);浙江理工大学研究生创新研究项目(YCX13016)
叶晓露(1989—),女,硕士生。主要研究方向为人体工程与数字服装。邹奉元,通信作者,E-mail:zfy166@zstu.edu.cn。

