应用Kronecker积的表里换层双层组织矩阵设计

王 旭，袁惠芬，刘新华

(1.安徽工程大学纺织服装学院，安徽 芜湖 241000;2.安徽工程大学纺织行业科技公共服务平台，安徽 芜湖 241000)

应用Kronecker积的表里换层双层组织矩阵设计

王 旭1，2，袁惠芬1，刘新华1，2

(1.安徽工程大学纺织服装学院，安徽 芜湖 241000;2.安徽工程大学纺织行业科技公共服务平台，安徽 芜湖 241000)

为提高双层组织的设计效率，提出一种基于矩阵Kronecker积的表里换层双层组织矩阵生成方法。按照表里换层双层组织设计的构造原理，建立表、里组织矩阵、纹样矩阵及叉积元，并运用Kronecker积实现了表里换层双层组织矩阵的自动生成。结果表明:采用矩阵Kronecker积运算，可以方便地实现表里换层双层组织矩阵的设计。随表、里基础组织矩阵、叉积元及纹样矩阵的不同，可自动生成不同类型的表里换层双层组织矩阵。这种方法丰富了表里换层双层组织的设计思路，可提高设计效率。

双层组织;Kronecker积;矩阵;表里换层组织

双层组织由2个系统的经纱和2个系统的纬纱交织而成，其织物具有厚重、坚牢、耐磨性好等特点，在服用毛织物、鞋面织物、装饰织物及产业用纺织品中应用广泛。传统手工方法进行双层组织设计，费时且易出错，如何提高设计效率已引起关注。已开展的研究以单层组织矩阵模型的建立为主，研究方法主要包括数学函数的组织异化法和矩阵变换法。数学函数的组织异化是通过函数曲线与组织图方格的相互关系来建立织物组织［1］。如采用数学函数的组织异化法，可建立加强斜纹、复合斜纹等变化组织矩阵［2－3］。矩阵变换是通过对元素或向量进行移位、转置、对称、取反等操作，实现多种组织矩阵的建立［4］。和单层组织相比，双层及多层组织矩阵模型的建立更复杂，传统的手工设计容易出错［5］。如多层织物组织设计，需要在组织图上设置多种标记，以区别各层不同性质的组织点［6］。目前针对表里换层组织［7］，双层组织矩阵模型［8］建立方法的研究尚不多见。其中矩阵Kronecker积对组织矩阵模型的建立具有较好效果［9－10］。本文通过对表组织、里组织矩阵及纹样矩阵等进行Kronecker积运算，探讨了双层组织、表里换层双层组织矩阵模型的建立。该方法拓展了双层织物组织矩阵建模的设计思路，提高了设计效率。

1 表里换层双层组织的矩阵表示

1.1 双层组织的矩阵表示

双层组织由2组经纱(表、里经)和2组纬纱(表、里纬)按照表、里组织交织规律和一定的排列比交织而成。为保证织物平整及织造过程顺利，表、里组织交织次数应接近，一般采用相同且简单的组织，如平纹斜纹和方平等。

单层组织由1组经纱和1组纬纱交织，交织规律可映射为二维布尔矩阵，元素1、0分别表示经、纬浮点。双层及多层组织经、纬纱均不止1组，可采用三维矩阵反映多组经纱和多组纬纱在各层内及层间交织规律，但三维矩阵对织造操作不够直观，常转换为二维矩阵，用不同的元素表示相应的信息。例如，图1示出表里组织均为斜纹，表、里经，表、里纬排列比均为1∶1时，双层组织及矩阵示意图。矩阵元素对应浮点性质如下:表组织经、纬浮点分别采用元素1、0表示，里组织经、纬浮点可分别采用元素3、2表示，织里纬时表组织经纱全部提起产生的经浮点用元素5表示等。织表纬时表纬与里组织经纱交织处的纬浮点仍采用元素0表示。

1.2 表里换层组织的矩阵表示

表里换层双层组织通过交换表、里2层的位置和纱线颜色的合理配置，实现不同的显色单元，并进一步运用显色单元的配置表现出织物的几何纹样。例如，图2示出表里换层组织显色单元组织及矩阵示意图。矩阵元素对应的浮点性质，同图1所示双层组织。

图1 双层组织及矩阵示意图Fig.1 Sketch of double-layer weaves and weaves matrix.(a)Face weaves;(b)Back weaves;(c)Double-layer weaves;(d)Matrix of face weaves;(e)Matrix of back weaves;(f)Matrix of double-layer weaves

图2 表里换层显色单元组织及矩阵示意图Fig.2 Sketch of color unit of thread interchanging weaves and weaves matrix.(a)Color A unit;(b)Color B unit;(c)Matrix of color A;(d)Matrix of color B

表里换层组织通过显色单元实现几何纹样。其中纹样矩阵的每个元素表示一种显色单元。为了简化处理，纹样矩阵可用布尔矩阵表示，其中1、0分别表示甲色和乙色单元，每个显色单元均表示为表里换层矩阵中的一个子矩阵。例如，图3(a)、(b)为显甲色和显乙色单元构成的两色方块纹样和“H”纹样，图3(c)、(d)示出相应的纹样矩阵。图中元素1、0分别表示显甲色单元和显乙色单元。本文以图3(a)为纹样，表、里组织均为斜纹，表里经、表里纬排列比均1∶1，说明表里换层组织矩阵的构成方法。由图3(c)得到图3(a)的4×4纹样矩阵，将元素1、0分别换成图2(c)、(d)所示的8×8矩阵，这样得到表里换层组织32×32矩阵，即完全组织经纬纱均为32根。织造时，表经、里经颜色从左到右，表纬、里纬颜色从下到上，均按照1甲色1乙色交替配置。

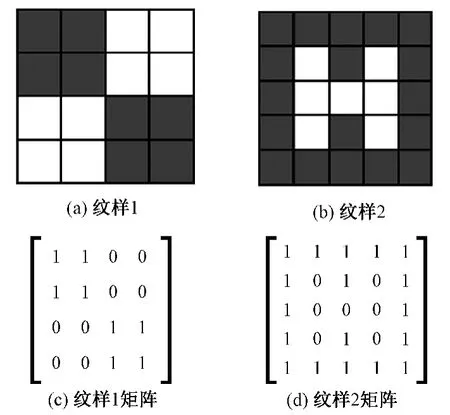
图3 表里换层组织的纹样矩阵Fig.3 Pattern matrixes of thread interchanging weaves.(a)Pattern 1;(b)Pattern 2;(c)Matrix of pattern 1;(d)Matrix of pattern 2

2 表里换层双层组织矩阵的生成

2.1 矩阵的Kronecker积

若A为m行n列矩阵，aij为矩阵A的元素。B为p行q列矩阵，那么式(1)表示的m×p行，n×q列矩阵C为矩阵A和B的Kronecker积。

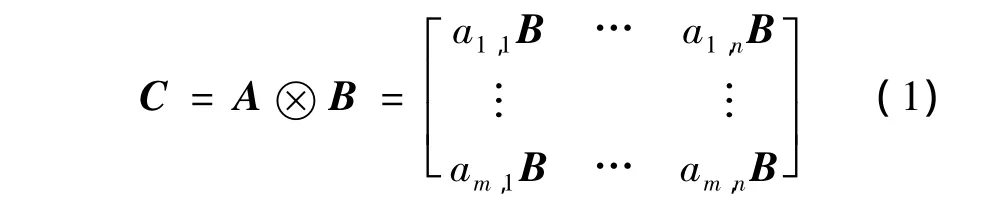
根据上述定义，结合双层和表里换层组织的构作原理，并进行运算，即可建立双层和表里换层组织的矩阵模型。

2.2 双层组织矩阵的生成

本文以图1所示的表里组织说明双层组织矩阵的生成。双层组织矩阵D的行和列为表组织矩阵A(或里组织矩阵B)行和列的2倍。首先将表组织矩阵A各元素，按次序放置在双层组织矩阵D的偶数行和奇数列交点的位置。里组织矩阵B各元素，则按次序放置在双层组织矩阵D的奇数行和偶数列交点的位置。最后将表经和里纬交织处，即矩阵D的奇数行和奇数列交点的位置全部赋值为5即可。上述过程可用Kronecker积实现，见式(2)。

式中，矩阵A、B分别对应图1(d)、(e)所示的表里组织矩阵。矩阵C为与表里组织行列一致的、元素均为5的矩阵，其作用是和叉积元 K3进行Kronecker积运算后，使矩阵D奇数行和奇数列交点的位置全部赋值为5，表示织里纬时表经提起。矩阵C及叉积元K1，K2，K3分别如下:

2.3 表里换层组织矩阵的生成

根据表里换层组织的构做方法，首先由表、里基础组织和表里经、表里纬排列比，建立显甲色矩阵A1、显乙色矩阵B1。由纹样图建立纹样矩阵H。根据置换法，将纹样矩阵H及其底片组织矩阵H'，分别和显色组织矩阵A1、B1进行Kronecker积计算，并将计算结果相加，见式(3)，即可得到表里换层组织矩阵W。

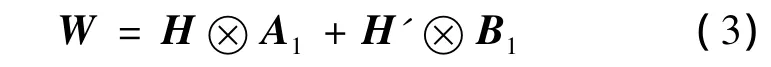
式中，显色矩阵A1，B1可根据式(2)进行计算，即:

式中:矩阵A、B分别表示表、里组织;矩阵C为全5元素矩阵，叉积元为

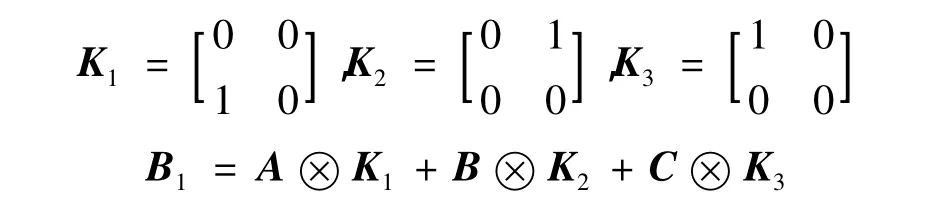
式中，叉积元为

2.4 实例

为了验证Kronecker积进行双层组织矩阵设计的效果，本文以实例进行说明。

若产生图3(b)所示的H型纹样，纹样矩阵H为5×5，选定表里组织均为方平组织，表里经，表里纬排列比均为1∶1。那么纹样矩阵每个元素将对应的显色单元矩阵为8×8，则表里换层矩阵为40×40。根据式(3)，带入相应矩阵，进行Kronecker积，即产生表里换层组织矩阵。图5示出根据矩阵绘制的组织图，其中元素0，2绘“□”，元素1绘“■”，元素3绘“×”，元素5绘“○”。

图4 双层组织矩阵实例Fig.4 Examples of double-layer weaves and weaves matrixes.(a)Face weaves;(b)Back weaves;(c)Double-layer weaves;(d)Matrix of face weaves;(e)Matrix of back weaves;(f)Matrix of double-layer weaves

图5 表里换层组织设计实例Fig.5 Example of thread interchanging weaves

纹样矩阵H如图3(d)所示，其底片组织矩阵H'可由矩阵H进行元素1，0互换即可得到。显色矩阵A1，B1参考2.3小节分别根据式(2)计算，其中表里组织矩阵A，B如图4(d)、(e)所示。显甲色组织及矩阵A1如图6(a)、(c)所示，显乙色组织及矩阵B1如图6(b)、(d)所示。织造时，表经、里经颜色从左到右，表纬、里纬颜色从下到上，均按照“1甲色1乙色”交替配置。

图6 表里换层组织显色组织及矩阵Fig.6 Color units of thread interchanging weaves.(a)Unit of color A;(b)Unit of color B;(c)Matrix of color A;(d)Matrix of color B

3 结论

根据双层组织的构做原理，讨论了基于矩阵Kronecker积的表里换层双层组织矩阵生成方法，并实现了相应矩阵模型的建立。结果表明，通过矩阵Kronecker积方法，可以快速生成双层组织、表里换层双层组织，该方法为简化、加速该类组织设计过程提供了参考，为今后进一步研究接结双层组织矩阵的自动生成打下基础。

［1］ 顾平.数学函数的组织异化数学模式:织物规则组织CAD 的新生成法［J］.丝绸，2001(11):9－11，22.GU Ping.The mathematical models for weave differentiation with mathematical function:a new algorithm for the regular weave CAD［J］.Silk Monthly，2001(11):9 －11，22.

［2］ 陈俊琰，汪军.变化及复杂织物组织的计算机自动生成［J］.东华大学学报:自然科学版，2007，33(2):207－211.CHEN Junyan，WANG Jun.Computer simulation for derivative weave and composed weave［J］.Journal of Donghua University:Natural Science Edition，2007，33(2):207－211.

［3］ CHEN Junyan，WANG Jun.A method of computer simulation of derivative weave and composed weave［J］.Journal of Donghua University，2006，23(6):97 －100.

［4］ 王旭，袁惠芬.基于矩阵变换的斜纹变化组织矩阵生成方法［J］.安徽工程大学学报，2011，26(4):20－23.WANG Xu，YUAN Huifen.A matrix generation method twill derivative weaves by matrix transform［J］.Journal of Anhui Polytechnic University，2011，26(4):20 －23.

［5］ 聂建斌，何奕中.多层机织物的组织设计［J］.纺织学报，2010，31(2):50 －53.NIE Jianbin，HE Yizhong.Weave design of multi-layer woven fabric［J］.Journal of Textile Research，2010，31(2):50－53.

［6］ 张国辉.多层织物的组织设计［J］.毛纺科技，2004，32(3):52－55.ZHANG Guohui.The design of weave diagram for multiple structrue［J］.Wool Textile Journal，2004，32(3):49－52.

［7］ 白燕.表里换层配色花纹织物的设计［J］.毛纺科技，2007，35(3):49 －52.BAI Yan.Research on color-patterned design of interchangeable double cloth［J］.Wool Textile Journal，2007，35(3):49－52.

［8］ 祝成炎.大循环双层多臂组织CAD技术的研究［J］.纺织学报，2001，22(6):37 －38.ZHU Chengyan.CAD for double-layer dobby weaves with large repeat［J］.Journal of Textile Research，2001，22(6):37－38.

［9］ 王旭，毕松梅.Kronecker积在变化绉组织设计中的应用［J］.纺织学报，2012，33(5):40 －45.WANG Xu， BI Songmei. Application of Kronecker product on derivative crepe weave design［J］.Journal of Textile Research，2012，33(5):40－45.

［10］ 顾平，丁立新.计算机生成双层组织的计算方法:Kronecker积的应用［J］.苏州丝绸工学院学报，1995，15(2/3):28－39.GU Ping，DING Lixin.The algorithm for double weaves constructed by computer:application of Kronecker product.［J］.Journal of Suzhou Institute of Silk，1995，15(2/3):28－39.

Matrix design for thread interchanging double-layer weaves using Kronecker product

WANG Xu1，2，YUAN Huifen1，LIU Xinhua1，2
(1.College of Textile and Clothing，Anhui Polytechnic University，Wuhu，Anhui241000，China;2.The Science and Technology Public Service Platform for Textile Industry，Anhui Polytechnic University，Wuhu，Anhui241000，China)

To improve the efficiency for design double-layer weaves，the generation method of thread interchanging double-layer weaves matrix based on Kronecker product was studied.According to the design rule for thread interchanging double-layer weaves，the matrix of face weave，the matrix of back weaves，the matrix of pattern，and the Kronecker unit were established，and then the weave matrix resulted from double-layer with thread interchanging weaves was fulfilled by the Kronecker product method.The results indicated that the Kronecker product can be used to design thread interchanging double layer weaves.Meanwhile，different styles of thread interchanging double-layer weaves matrixes could be automatically generated with different face basic weave matrixes，back basic weave matrixes，Kronecker units and pattern matrixes.This method expands design idea and provides an effective tool for thread interchanging double-layer weaves.

double-layer weaves;Kronecker product;matrix;thread interchanging weaves

TS 105.1

A

10.13475/j.fzxb.20140302005

2014－03－10

2015－01－19

安徽省高等学校省级自然科学研究项目(KJ2013B024);安徽工程大学科研启动基金项目(2012YQQ008)

王旭(1973—)，男，副教授，博士。研究方向为织物组织CAD设计。E-mail:wangxu_ahpu@hotmail.com。