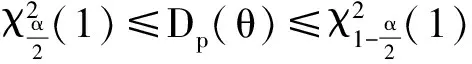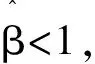Pareto分布中尺度参数的区间估计
王 娟,徐付霞
(天津工业大学 理学院,天津 300387)
Pareto分布中尺度参数的区间估计
王 娟,徐付霞
(天津工业大学 理学院,天津 300387)
研究了枢轴量法、极大似然估计的渐近正态性法和轮廓似然函数法,求解了Pareto分布中尺度参数的置信区间.通过生成随机数进行数值模拟分析,得出区间估计和区间长度,对这几种区间估计方法进行了比较.
Pareto分布;枢轴量;极大似然;轮廓似然
近年来,一些文献已对比较常见分布的未知参数的区间估计问题进行了研究,解决了很多与之相关的实际问题,如正态分布中均值的区间估计和学生成绩之间的关系;指数分布中,参数的区间估计和组件寿命之间的关系等[1].Pareto分布作为一种收入分布由意大利经济学家Pareto提出,它不仅在经济收入模型中得到应用,在其他领域中也得到了广泛的应用.可以用它描述各种社会经济、物理以及生物现象,例如城市人口、股票价格、商业失效、江河流量和某种药理过后病人的存活时间等,而且在军事、天文领域也得到了广泛应用[2].在此之前,很多文章只研究了Pareto分布参数的多种点估计方法,而研究Pareto分布中参数的区间估计更有意义,便于人们对各种实际问题进行更加全面深入地探讨.因此,本文给出Pareto分布中尺度参数的几种区间估计方法,重点研究之前不常见的极大似然估计的渐近正态性法和轮廓似然函数法,并说明这几种方法的适应范围及优缺点.
1 预备知识
1.1 枢轴量[3]
一般来说,欲构造θ的置信水平为1-α的置信区间,我们首先考虑θ的极大似然估计MLE,或θ的充分统计量T=T(X),并基于T(X)寻找枢轴量,然后构造θ的置信区间.在统计量T(X)是连续型随机变量时,设T(X)的分布函数为G(t;θ)=Pθ{T(X)≤t},那么G(T(x)t;θ)~U(0,1),U(0,1)为(0,1)上的均匀分布,此时G(T(X);θ)可被取为枢轴量.
选取两个常数c和d(0 Pθ{c≤G(T(X);θ)≤d}=1-α (1) 通过求解由式(1)确定的关于θ的不等式c≤G(T(X);θ)≤d就可得到θ的置信水平为1-α的置信区间. 1.2 极大似然估计的渐近正态性[4] 极大似然估计是使用极为广泛的一种参数估计方法,使用该估计的最大优点是能得到抽样分布的渐近分布,从而得到标准误和置信区间的近似值.设随机变量X的分布函数为F∈{F(x;θ)∶θ∈Rd},(d≥1).X1,…,Xn是X的一个样本,(·)和分别表示对数似然函数和参数向量θ=(θ1,…,θd)的极大似然估计,则在一定的正则条件下,当n充分大时,有 其中“A”表示渐近分布,Nd表示d维正态分布,矩阵 IE(θ)度量了对数似然函数的期望曲率,称为Fisher信息阵. 其中:Z1-α/2表示标准正态分布的1-α/2分位数,以下同. (2) 通常这个区间比用Fisher信息阵得到的区间更精确. 1.3 轮廓似然函数[5] 当总体分布含有两个以上的参数,而我们只对其中的某个或某几个感兴趣时,可以用轮廓似然函数方法求解其置信区间.这种方法可以避免未研究的参数对所研究参数的区间估计造成影响. 设θ=(θ(1),θ(2)),θ(1)表示θ中感兴趣的k维分量,θ(2)表示θ的其他d-k维分量,也称为讨厌参数.θ(1)的轮廓似然函数定义为 即对每个θ(1)的值,轮廓似然函数就是除θ(1)之外,似然函数对所有其他分量求最大值.在适当的正则条件下,当n充分大时,有 Dp(θ(1))=2{ Dp(θ(1))=2{p(θ(1))}称为偏差度函数表示自由度为k的卡方分布.对于给定的显著性水平α,有 成立,由此可得θ(1)的置信水平为1-α的置信区间为 (3) 设总体X服从参数为β,θ的Pareto分布,其概率密度为 (4) 其中:β为形状参数,θ为尺度参数,或称门限参数.本文对尺度参数θ作区间估计,对于形状参数β分两种情况研究. 2.1 β已知时,θ的区间估计 我们可以用两种方法得到θ的区间估计: 2.1.1枢轴量法 (5) 其中I(θ,+∞)(x(1)是示性函数,X(1)=min{X1,…,Xn},x(1)是X(1)的观测值. 使式(5)达到最大,就得到参数θ的极大似然估计 . (6) 下面求X(1)的分布函数,由式(4)可得Pareto分布的分布函数为 于是X(1)的密度函数和分布函数分布为 任选取两个常数c和d(0 从而θ的置信水平为1-α的置信区间为 区间长度为 可见区间平均长度关于c递增,取最小的c值,c=0,就得到平均长度最短的置信度为1-α的置信区间为 (7) 2.1.2极大似然估计的渐近正态性法 相应的1阶观测信息矩阵为 由1.2节的式(2)得θ的近似置信度为1-α的置信区间为 (8) 多数情况下,参数β事先未给定,这时β不能直接用于对参数θ的估计,我们可以采用以下方法求解θ的估计. 2.2 当未β知时,θ的区间估计 2.2.1极大似然估计的渐近正态性法 (9) 使式(9)取得最大值,就得到的极大似然估计 (10) (11) 由1.2节的式(2)得θ,β的置信度为1-α的置信区间分别为 (12) 2.2.2轮廓似然函数法 由式(9)得θ的轮廓似然函数为 对任意θ,欲使(θ,β)取最大值,需对(θ,β)关于β求导,并令其为0,即得 (13) 则 偏差度函数为 Dp(θ)=2{ 则对给定的α,有 成立,即 (14) 3.1 β已知,对θ的区间估计的数值模拟 假设β=0.5已知(为0.5),通过Matlab软件生成n=16个服从参数θ=10的Pareto分布的随机数如下[6]: 32.425,145.863,1448.172,23.907,67.620,14.705,28.806,286.610,230.913,28.327,883.347,10.201,1635.349,2403.728,11.355,13.507 进一步,选取不同的样本容量n,生成服从参数β=0.5,θ=10的Pareto分布的随机数,得到两种估计方法对应的置信区间,其长度分别为L1,L2,见表1. 表1 β已知时,两种估计方法的区间长度 为了更直观的看出L随样本容量n的变化趋势,画出n与两种方法得到的区间长度之间的变化关系图,如图1(A). 图1 区间长度随n的变化关系图 由图1可见,枢轴量法得到的区间估计长度L1比极大似然估计的渐近正态性法得到的区间估计长度L2短.当样本容量n较小时,枢轴量法和极大似然估计的渐近正态性法所得的区间估计长度都较大,随着样本容量n的逐步增大,两种估计方法的区间长度逐渐减小,精度提高,两者越来越接近且趋于平稳(随着的增大,图中曲线斜率变化幅度越来越小).为了保证估计的精度,我们多数采用枢轴量法,但当枢轴量过于复杂难于求解,并且样本容量足够大时,极大似然估计的渐近正态性法也不失为一种好的区间估计方法. 3.2 β未知,θ对的区间估计的数值模拟 利用Matlab软件,生成了n=16个服从参数β=0.1,θ=0.2的Pareto分布的随机数为: 1.274×104,155.352,19.291,18.349,393.295,3.866×107,18.327,2.333, 1.076×1010, 2.209, 2.098×104, 1.847×106, 3.631, 8.923,47.963,722.575. 再应用轮廓似然函数法得到偏差度函数 对于给定的显著性水平α有 可见,当β未知时,通过上述两种方法得到的θ的区间估计,轮廓似然函数法的区间长度较极大似然估计的渐近正态性法的区间长度h2短.为了进一步对两种方法作出比较,现取不同的样本容量n,得到两种估计方法对应的区间长度,分别为h1,h2.如表2. 表2 未知时,两种估计方法的区间长度 相应地,区间长度h随样本容量的变化关系如图1(B) . [1] 蒋福坤, 刘正春. 指数分布参数的最短区间估计[J]. 数理统计与管理, 2004, 23(3): 43-45. [2] 李海芬.Pareto分布的统计分析. [D]. 上海: 华东师范大学, 2004. [3] 茆诗松, 王静龙. 高等数理统计[M]. 北京: 高等教育出版社, 2004. [4]STUARTC.AnintroductiontoStatisticalModelingofExtremeValue[M].NewYork:Springer, 1990. [5] 史道济. 实用极值统计方法[M]. 天津:天津科学技术出版社, 2005. [6]NELSENRB.Anintroductiontocopulas[M].NewYork:Springer, 1998. [7] 茆诗松 ,程依明. 概率论与数理统计教程[M]. 北京: 高等教育出版社, 2004. Interval estimates on shape parameter of Pareto distribution WANG Juan, XU Fu-xia (School of Science, Tianjin Polytechnic University, Tianjin 300387, China) In this paper, the methods of pivot quantity, the asymptotic normality of maximum likelihood estimate and the profile likelihood function were used to solve the confidence interval of the shape parameter of Pareto distribution. Calculated the interval estimation and interval length by generating more groups of random numbers and carry on the comparison to the interval estimation methods. Pareto distribution; pivot quantity; max likelihood; profile likelihood 2015-02-27. 王 娟(1990-),女,硕士,研究方向:极值统计. O212 A 1672-0946(2015)05-0629-05

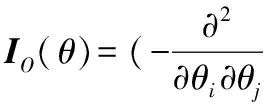

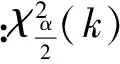
2 Pareto分布中尺度参数的区间估计



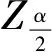

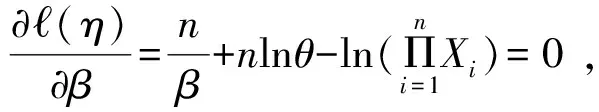



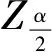
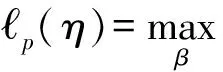

3 数值模拟分析