双分数布朗运动下再装期权定价模型

薛 红，吴江增

(西安工程大学 理学院，西安 710048)

双分数布朗运动下再装期权定价模型

薛 红，吴江增

(西安工程大学 理学院，西安 710048)

在标的资产服从双分数布朗运动驱动的随机微分方程，借助双分数布朗运动随机分析理论，建立双分数布朗运动环境下金融市场数学模型，运用保险精算方法，得到了双分数布朗运动环境下再装期权定价公式.

双分数布朗运动；再装期权；保险精算

近几年，由于金融市场的飞速发展，标准的期权已经不能满足金融市场的需要，于是各种新型期权逐渐进入复杂的金融市场. 再装期权就是一种新型的欧式看涨期权.文献[1]首次给出了布朗运动下的再装期权定价公式.文献[2]运用鞅方法给出了股票价格服从跳-扩散过程的再装期权的定价公式.文献[3]运用拟-鞅的方法给出了标的资产价格服从分数布朗运动下的再装期权定价公式.文献[4]首次提出了双分数布朗运动，指出双分数布朗运动是比分数布朗运动更一般的中心高斯过程. 本文在标的资产价格服从双分数布朗运动的前提下，利用保险精算的方法导出了双分数布朗运动环境下再装期权定价公式.

1 双分数布朗运动环境下金融市场模型

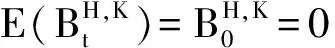
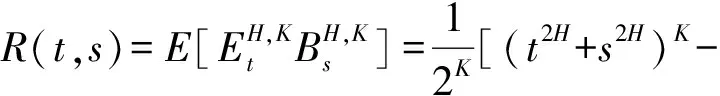
其中:H∈(0,1),K∈(0,2).

当K=1时，双分数布朗运动即为参数为H∈(0,1)的分数布朗运动；特别地，当K=1,H=1/2时，双分数布朗运动即为标准布朗运动. 关于双分数布朗运动相关性质和随机分析基本理论可见文献[4].

假定金融市场中存在一种无风险资产(债券)和一种风险资产(股票)，其价格分别满足方程

dMt=rMtdt,

(1)

(2)

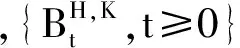
引理1[5]随机微分方程(2)的解为

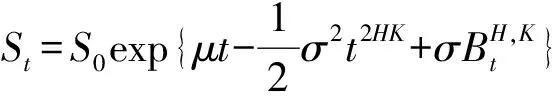
定义2[6]价格过程{St,t≥0}在[0,t]时间段内的期望收益率βu,u∈[0,t]定义为

引理2 {St,t≥0}在[t,T]上的期望收益率为βu=μ,u∈[0,t]

证明 由引理1知

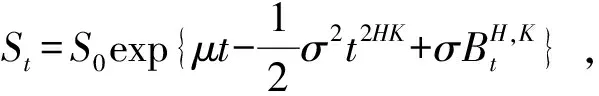
且

则

从而可得结果.

2 再装期权定价公式

假设在到期日T之前只考虑再装一次情况下，则再装期权的收益结构：在再装日T1(0

当T1→T时，再装期权即为欧式看涨期权.

定义3 再装期权的保险精算价格定义为

C=E{[exp{-μT1}ST1-exp{-rT1}K]I{exp{-μT1}ST1>exp{-rT1}K}}=

+E{[exp{-μT}ST-exp{-rT}K]Iexp{-μT1}ST1exp{-rT}K}}

其中无风险资产按无风险利率r折现，风险资产按其期望收益率β折现.

定理1 双分数布朗运动环境下再装期权保险精算价格

C=S0N(d2)-Kexp{-rT1}N(d1)

其中

d7=d1+ρ2σTHK,d8=d6+σTHK

证明 令

C1=E{[exp{-μT1}ST1-exp{-rT1}K]I{exp{-μT1}ST1>exp{-rT1}K}},

C3=E{[exp{-μT}ST-exp{-rT}K]Iexp{-μT1}ST1exp{-rT}K}}

1) 计算C1，由于

所以

C1=E{[exp{-μT1}ST1-exp{-rT1}K]=Iexp{-μT1}ST1>exp{-rT1}K}=

S0N(d2)-Kexp{-rT1}N(d1).

2) 计算C2，由于

则

令

则

3) 计算C3，由于

C3=E{[exp{-μT}ST-Kexp{-rT}]Iexp{-μT1}ST1exp{-rT}k}}}

令

x1=x-ρ2σTHK,z1=z-σTHK,

则

-Kexp{-rT}N(-d1,-d6,ρ2) 从而定理得证.

注1)当K=1时，可得分数布朗运动环境下再装期权定价公式(见文献[7])；

2)当T1=T时，可得双分数布朗运动环境下欧式看涨期权定价公式

c=S0N(d2)-Kexp{-rT}N(d1)

其中

d2=d1+σTHK

[1] JOHNSON S A, TIAN Y S. The value and incentive effects of nontraditional executive stock option plans [J]. Journal of Financial Economics, 2000, 57: 3-34.

[2] 冯广波, 刘再明, 候振挺. 服从跳-扩散过程的再装期权股票期权的定价[J]. 系统工程学报, 2003, 18(1): 91-93.

[3] 罗春玲, 王晓勤. 股票价格服从分数布朗运动的再装期权定价[J]. 价值工程, 2011(13): 143-144.

[4] RUSSO F, TUDOR C. On the bifractional Brownian motion [J]. Stochastic Processes and Applications, 2006, 116(5): 830-856.

[5] 肖玮麟, 张卫国, 徐维东. 双分式布朗运动下股本权证的定价[J]. 系统工程学报, 2013, 28(3): 348-354.

[6] 张雪莲, 薛 红. 分数布朗运动环境下重置期权定价模型研究[J]. 西安工程大学学报, 2009, 23(4): 141-145.

[7] 何永红, 薛 红, 王晓东. 分数布朗运动环境下再装期权的保险精算定价[J]. 纺织高校基础科学学报, 2012, 25(3): 384-387.

[8] 符 双，薛 红.分数跳-扩散O-U过程下幂型期权定价[J]. 哈尔滨商业大学学报：自然科学版，2014，30(6)：758-762.

Reload option pricing model in bi-fractional Brownian motion environment

XUE Hong, WU Jiang-zeng

(School of Science, Xi’an Polytechnic University, Xi’an 710048, China)

Underlying asset process follows the stochastic differential equation driven by bi-fractional Brownian motion. The financial market mathematical model is built by the stochastic analysis for bi-fractional Brownian motion. Using the actuarial approach, the pricingformula of reload option in bi-fractional Brownian motion environment is obtained.

bi-fractional Brownian motion; reload option; actuarial method

2015-03-10.

陕西省教育厅自然科学专项基金(12JK0862)

薛 红(1964-)，男，博士，教授，研究方向：随机分析与金融.

O211

A

1672-0946(2015)06-0765-04