雾霾逾渗动力机制及临界态下大气的治理
郑小京,郑君君,李 超
(1.哈尔滨商业大学商业经济研究院,哈尔滨150028;2.武汉大学经济与管理学院,武汉430072;3.上海交通大学中美物流研究院,上海200030)
近年来,中国雾霾形成的范围、程度以及频率越来越大,这一切现象似乎突如其来,没有任何预兆.科学研究的结果表明,雾霾的主要成分就是PM2.5与 PM10,而 PM2.5已经被证实确实是一种致癌物,故此,对雾霾的治理已经成为关系国计民生的大事.由于雾霾发生的频率、程度都在不断的增大,有一些科学家在猜想,空气质量由优质空气到雾霾的相变时代是否已经到来,如果这种猜想可信,那么就可以得到下一步结论:我们国家的大气正在处于临界状态上,即处于洁净空气这一相与雾霾相这一相中间的接续态中,这种情况下,一个微小的扰动(废气排放量、温度、湿度、风速、天气状况<晴、阴、雨等>等的微弱的扰动)都可能导致系统状态从一个相到另一个相迅速转换,这也是我国近些年雾霾频频发生且程度越来越强的本质原因.这种现象正如范德瓦尔斯处于接续态的水分子分析一样,“当流体发生状态变化,从气体变为液体或者反过来变化时,每个微粒本身并不发生改变.他们的行为依旧像些硬邦邦的小球,每个小球都有自己在短距离内发生作用的吸引力场.然而,他们的集体状态却截然的(而且突然)变得不大相同……”
既然我们将我国目前的空气质量状态定义为处于雾霾与洁净空气之间的接续态—临界状态中,那么,下列问题尤为关键:我们国家的空气真的是在临界区吗?如果在临界区,那么其最敏感的影响因素是什么,包括气体的排放量及其以及空气温度、湿度、风速、大地干旱程度、天气状况等噪声的状态与性质?临界点与排放气体总量之间什么关系?何种策略才能有效的对其进行治理?本文将这一系列问题进行比较深入的研究.
研究逾渗的科学家一致认为,雾霾的形成其实就是灰尘颗粒对大气分子污染从量变到质量的一个过程,这个过程呈现出很强的临界性、非线性,其本质为系统几何结构的强无序和强随机性.刘生丽等认为逾渗理论是为数不多的几种处理强无序和具有随机几何结构系统的理论方法中最好的一种,在治理环境污染时,通过建立模型,并应用逾渗理论可以找到逾渗阈值,即治理污染的最佳方法,使治理污染的费用降到最低[1].齐艳红等分析了生态环境收到损坏时逾渗的动力学特征[2],尽管这一结论与大气污染有一定的差距,生态环境被侵蚀的过程与大气被污染的过程具有强相似性,因此大气污染也是一个逾渗过程.
大气中排放物总量及其结构是雾霾的主要成因,正如逾渗理论以及研究大气污染的结论所证明的那样,在这一方面得到了一定的结论.张小曳等认为,现今的雾和霾,都已不是完全的自然现象,气溶胶污染是背后的主因,与人口众多和经济快速发展导致的人为污染源排放量大密切相关,认为沙尘、城市逸散性粉尘和煤烟尘等是北京地区的雾霾源中最关键源[3].徐敬等对北京空气样本进行粒子分析,然后采用 PMF(Positive Matrix Factorization)源解析方法确定了5类细粒子污染源,分别是:土壤尘、煤燃烧、交通运输、海洋气溶胶以及钢铁工业[4].王明珠等认为,北京地区农作物桔杆燃烧是PM2.5重要的来源之一,农作物桔杆燃烧产生的PM2.5排放总量随着年份的增加呈波动性上升趋势[5].马丽梅等认为,通过空间面板回归模型得到雾霾污染存在着显著的溢出效应,并且邻近地区的PM2.5浓度每升高 1% ,就会使本地区的 PM2.5浓度升高0.739%,能源消耗结构中煤炭所占比重与雾霾污染呈正向变动关系,它的变动与雾霾污染的变动息息相关[6].然而,目前尚没有统一的结论确认主要的污染源,存在很大的争议.
环境对雾霾的影响是非常显著的,这一结论已经得到了证明.陈媛等认为,温度、相对湿度、风速、降水和气压等是影响PM2.5污染程度的重要因素,不同季节里、不同温度范围内,PM2.5的质量浓度与温度表现出不同的但都强烈的相关性;沙尘天气里风速低于某一阈值(10 km/h)时,PM2.5的质量浓度与风速呈负相关,反之则呈正相关[7].赵晨曦等认为,不同大气污染物浓度(气体、颗粒)与气象要素之间的关系是非线性的,PM2.5和PM10的实时浓度与对应的气温、相对湿度显著正相关,而与风速显著负相关[8].邓利群等认为,PM2.5 和 PM10 质量浓度与气压的相关系数分别为 -0.25 ~ -0.31[9].由于这种气象因子的多变性与不可控性,造成了颗粒物浓度变化的复杂性,给研究带来非常大的困难.大量研究结果认为气象环境是雾霾的主要影响因素,这种外部噪声决定论的悖论提出一个命题:如果噪声是一个系统相变的最关键的因素,那么这个系统就一定处于临界状态.刘强等论证了这一问题,他认为,雾霾形成的主要原因是污染物排放总量的长期积累所形成的生态环境系统自净功能丧失,从而使得大气污染物无法消纳所致[10].
在本文中,我们主要对我国大气在雾霾逾渗临界状态的性质进行论证,以及在这一状态下,应该采取何种措施,才能起到较好的效果.
1 雾霾的临界性
从非平衡统计物理学角度看,大气粒子可以看成在三维空间中的晶格,每一个晶格中的大气粒子与相邻其他晶格中的大气粒子直接相互作用.大气中随机分布着一些尘埃,它们可以附着在大气粒子表面,这种被覆盖的大气粒子大小达到一定程度上就被称作烟尘颗粒,其密度超过某一特定的数值之后就形成了雾霾.
进一步讲,灰尘并不是均匀的而是随机的覆盖在一些大气粒子上.一般的,被覆盖的粒子表面上有一层灰尘,它们的表面积就增大,这个表面积越大,就越容易吸附更多的灰尘,从而也形成一种以“强度”为核心的“优先连接”机制.显然,这一系统符合无标度系统的属性.如果用网络来描述,可知这一系统实际上是一个无标度的随机复杂网络.而雾霾则可以看成是网络的同步逾渗现象.这一逾渗过程具有突发性,现在假定一个实验:在二维空间中有一个排放源,所排出的污染气体在空间扩散,最后“消失”在整个空间中;随着气体的排出,这种情况持续出现,系统仍然保持着“纯洁”;在某一瞬间,当有一小点废气被排放到这个系统中时,整个系统突然变成了废气所标记成的颜色,这种污染迅速传遍整个空间,并随着废气的排放迅速加重.假定存在两个不同状态的空气,分别为(a)与(d),如下图所示,当大气中的灰尘颗粒被排放之后,空气中的大部分粒子被污染,这种被污染的粒子(黑色部分)将在大气中扩散,当还有一些颗粒排出来之后,更多的空气颗粒被污染,某一时刻,突然大气中几乎所有的粒子似乎都被污染了.
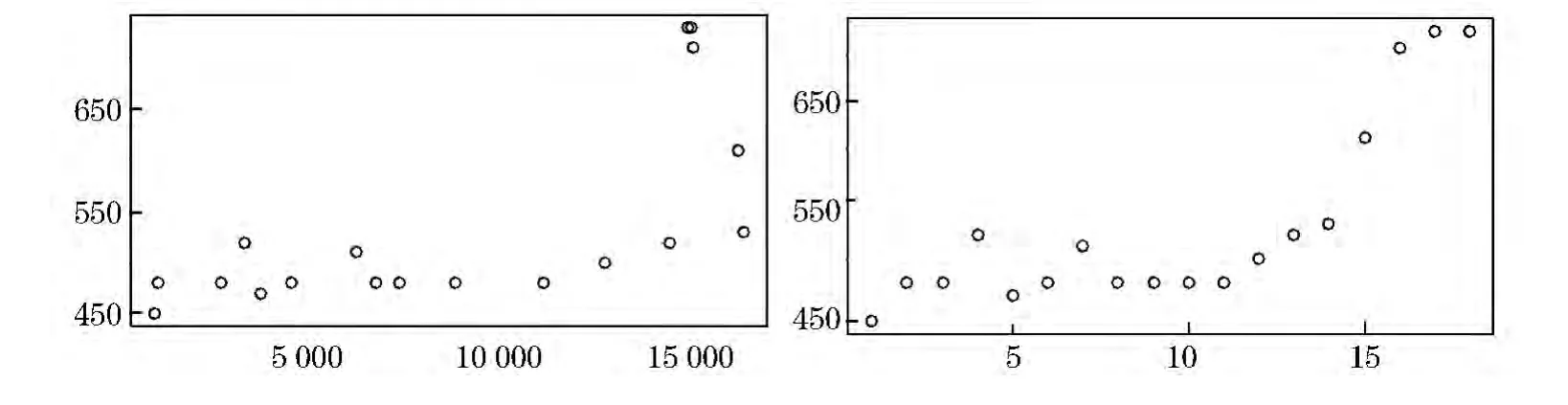
图1 废气排放量-大气质量散点图(左侧为正常坐标,右侧对横坐标进行了对数标度)
我们调查了北京市从1983~2013年空气质量指数与废气排放量的情况.值得注意的是,PM2.5是最近几年刚出来的一个观测变量,在前些年并没有这一指标.不过,参考赵晨曦的结论—北京市PM2.5和PM10的平均质量浓度存在较好的相关性,Spearman秩相关系数为0.867,P<0.01二者的比值范围为 0.31 ~0.96,均值为 0.72[8],我们可以估算出一个大致的PM2.5的值,然后通过与对应时间点上的空气质量指数的差异来调整,从而确定这一数值.这一期间北京市废气排放与空气质量指数之间的散点图如图1所示.
图1中,横坐标代表废气排放总量,为了更加清楚其变化情况,我们对这一总量进行了10-3的标度,使得坐标缩小到1/1 000;纵坐标表示空气质量指数,以PM10与PM2.5为参考取得的数据,这一数据不大于1,为了更能方便看清,我们将坐标进行了103的标度,使得坐标放大1000倍.从右侧的图中跟更容易看清雾霾形成的逾渗现象.
可以看出,当排放总量在15 000与17 500之间时,存在一个“拐点”,这一拐点使得空气质量迅速的下降.从图1中可以看到,我国空气质量目前仍然还处在临界区,雾霾还没有完全形成.进一步而言,我们从图中可以看出,当空气中颗粒数量超过这一临界点之后,即使是排放总量低于临界密度,大气质量仍然会恶化.这是因为在临界区时,空气处在一个超临界态上,在超临界态,系统二次相变的性质就特别显著,任何一个轻微的震荡,即使是变小,也会使得大气的性质发生突变,这种体现出很强的非线性滞后效应异常明显,这其实也说明了雾霾一旦形成,就非常顽固,难以进行治理.这种超临界态使得整个治理非常困难,但按照逾渗理论,我们还是可以将空气的质量低于雾霾逾渗的临界点,治理的可行性较高.
这种相变让我们生活质量有了很大的影响.那么一系列问题就被提出来:废气排放总量与空气质量之间的关系到底是什么,而温度、湿度、风速、季节这些气象因素对空气质量的影响是什么样的?人类排放的废气的行为之中,哪些是最关键、最敏感的?下面我们将重点分析这一问题.
2 雾霾逾渗动力学
与前面提到的临界性相对应,我们首先必须知道一个基本的原理:雾霾的形成在临界区是非线性的;第二,就所有的排放量而言,排放量最大的不一定就是关键因素,其增加值的波动大小也是考虑是否为关键因素的重要标准.原因很简单,由于其非线性所导致的临界性,雾霾所形成的相对发生比与所增加的量成线性相关.这一结论也被马先南证明,他认为,三维Mandelbrot渗流下临界形态,证明了渗流函数θ(p)在pc点是不连续的,同时得到当p<pc时,三维Mandelbrot渗流A的最大连通分支是点,即 A 是“尘状”的[11].同时,CHENG Jinrong等也认为,分形聚集的逾渗阈值仅取决于空间维数和近邻条件,与模型的网格大小无关,是分形系统固有的临界属性;生长概率等于逾渗阈值时,颗粒聚集体可以无限生长并保持分形维数恒定,此时的分形维数只是空间维数的线性函数[12].可见,这种逾渗过程中的非线性非常强,不能用线性思维的方式来解决,在维数比较高的情况下,更加复杂.不过也可以简化,正如SU Zhong-gen认为,这表明整数格点空间上AB-渗流模型的临界概率和它的子图上经典渗流模型的临界概率渐近相等[13].
下面我们构造一个对应的模型,来解释这一现象:不妨假设大气的区域是一个L×L×L的空间,在下部有一个排放源,其排放速度为,而排放口的大小不妨假设为l×l,因此,单位时间排放总量为l×l×v0,而这些颗粒扩散的速度为,因此扩散到外部的颗粒总量为5×L×L×,剩余在系统中的颗粒总量为5×L×L×-l×l×v0,并且=f(T,RH,v)(其中T表示温度,RH表示湿度,v表示风速),因此,大气系统中的分子将以概率p(T,RH,被污染,而以等概率1-p保持纯净的空气分子,则随着污染分子的扩散,这一系统中将形成大小为的颗粒聚集体,这一颗粒聚集体数量为N(s,p;L),不妨称其为-颗粒聚集体.定义表示颗粒聚集体的密度,由此可知

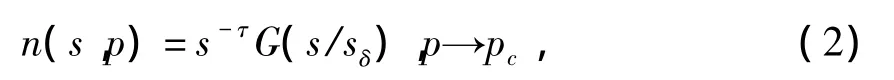
将G(s/sδ)泰勒展开,即可知道:

通过方程(1)~(3),我们可以确定出聚集体密度的分布情况,如果这一密度足够大,则会造成雾霾的逾渗.现在考虑下一个问题:这一聚集体可能出现的位置是什么,以及大气中可能的聚集体的平均大小是多少.为了解决这一问题,在s-聚集体选择位置的概率为s/Nocc,其中Nocc表示整个系统中单位空间的数量,则随机选择的聚集体的平均大小为
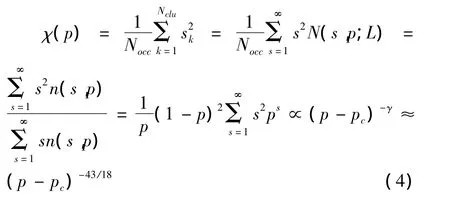
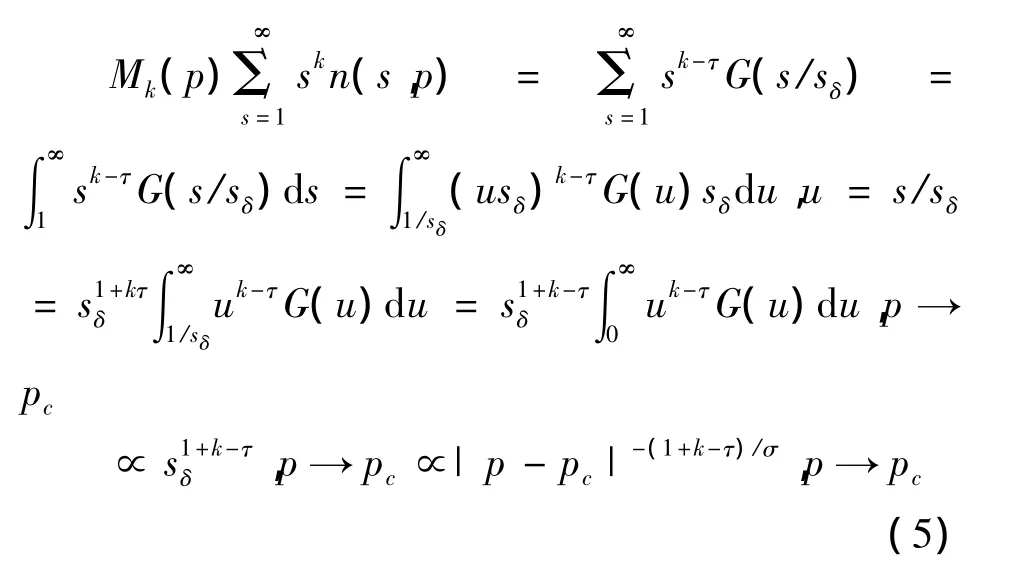
通过方程(4),可以确定出随机确定的颗粒聚集体的平均大小,令Mk为聚集体大小的k阶矩,则有我们引入另一个序参量P∞(p)=p-Σ∞s=1sn(s,p),可见这一序参量能够描述空气质量好坏,由此可知:
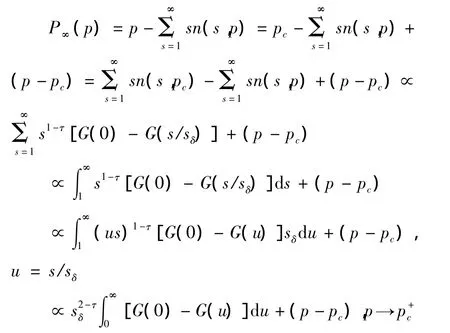
一般的,我们取G(x)=exp(-x),则有以下结果:
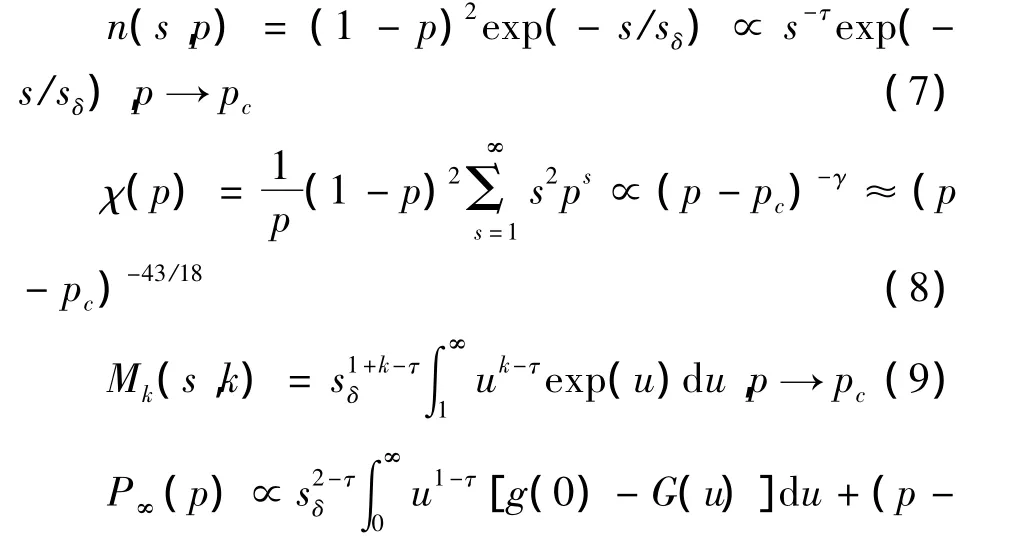

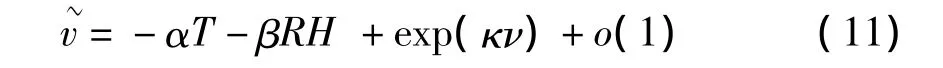
将式(11)代入其定义,联立方程,可以得到:
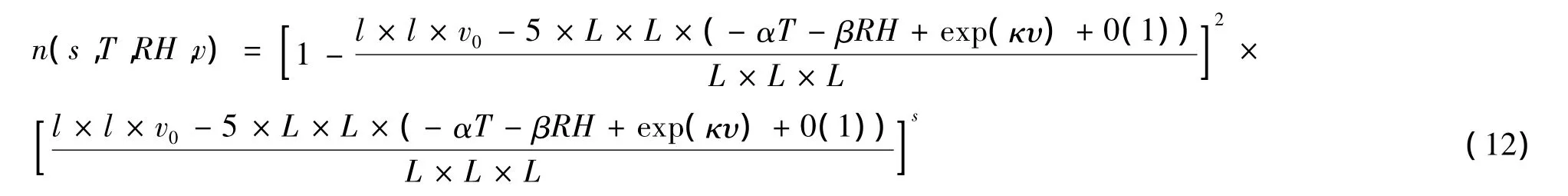
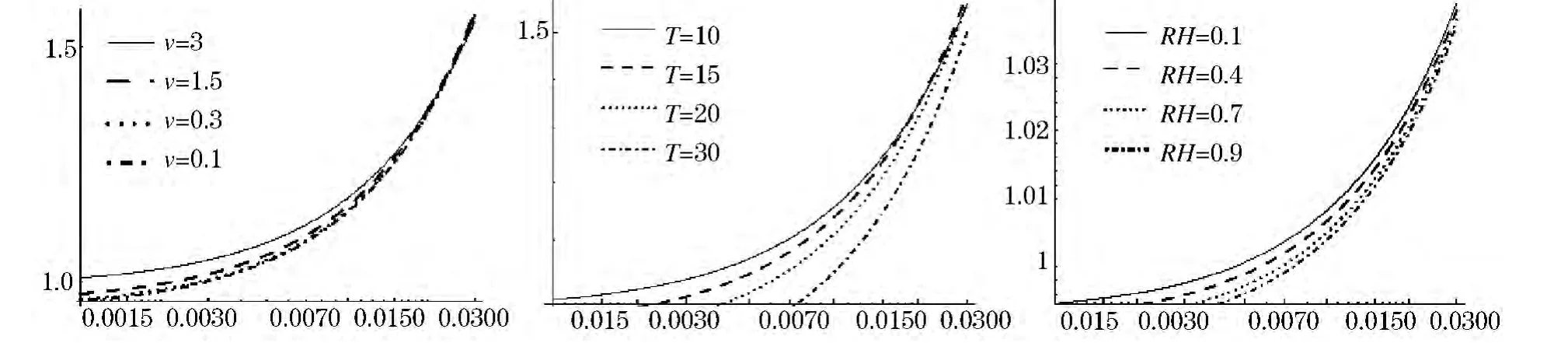
图2 n(s)-s双对数曲线图
图2中横轴表示连通起来的直径大小,纵轴特定直径大小的聚集体的数量,这个图描述s-聚集体数量随着聚集体直径的变化情况,其实就是空气质量好坏.图2分别描述了不同风速v、不同温度T以及不同湿度RH的影响变化情况.
显然,图2与图1与从根本上是一致的,均表示了大气雾霾具有一个逾渗的临界状态.不过,这一理论值与实际值相比较,稍微有一些差别,就是没有看到那个超临界态,其主要原因是在做图的过程中,没有考虑到其他因素的交互作用.而随机选择的聚集体的平均大小则可以通过下式来描述:

呈现出显著的分形属性.下面我们考虑聚集体 密度的k阶矩,可以知道
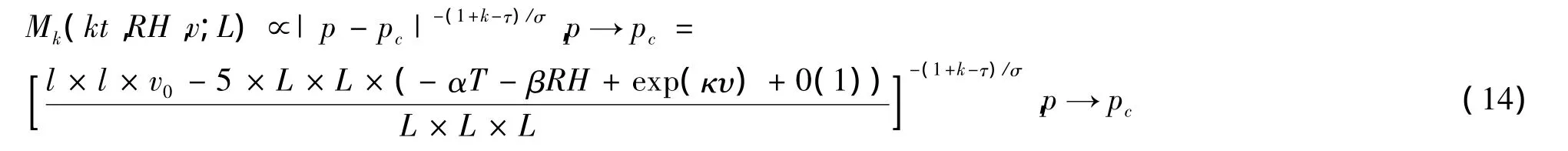
这一k阶矩具有图3所刻画的性质.进一步而言,聚集体密度的k阶矩描述了聚集体大小的性质,其中k=1表示聚集体平均大小,k=2表示聚集体大小的方差,k=3表示聚集体密度函数向左或向右偏斜的程度,k阶矩表示聚集体密度k次方的均值,描述了聚集体的统计属性,当然,这个统计量用于估计总体的粒子聚集体的各种未知参数时更有意义.
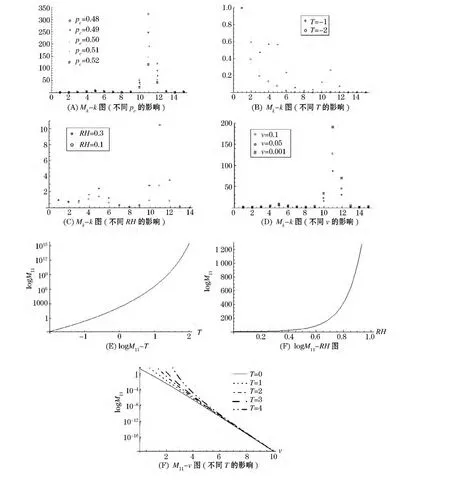
图3 Mk的性质
图3表示了k阶矩的分布,其中,(A)、(B)、(C)、(D)的横坐标为k,纵坐标为Mk,描述了聚集体密度的k阶矩大小随着k值变化的情况.从图中可以看出各个因素对11阶矩M11的影响差异非常大.因此(E)、(F)、(G)的横坐标分别为温度 T、湿度RH以及风速v,纵坐标仍然是Mk.进一步,(A)表示了不同临界密度pc对Mk的影响程度,(B)表示了不同温度T对Mk的影响程度,(C)表示了不同湿度RH对Mk的影响程度,(D)表示了不同的颗粒传播速度 v对 Mk的影响程度.(E)、(F)与(G)表示了温度T、湿度RH以及扩散速度v对M11的影响程度.
可以看出,聚集体密度的k阶矩的分布体现出非常有趣的性质,尤其是在k=11时,Mk对k以及其他参数的影响非常显著.总的来说,与温度T体现出来强烈的指数正相关关系,与湿度RH体现出强烈的临界特性—在50%~60%之间存在一个相变的临界点使得这种正相关突然发生,而与风速显著的指数负相关.下面我们分析的性质,可知
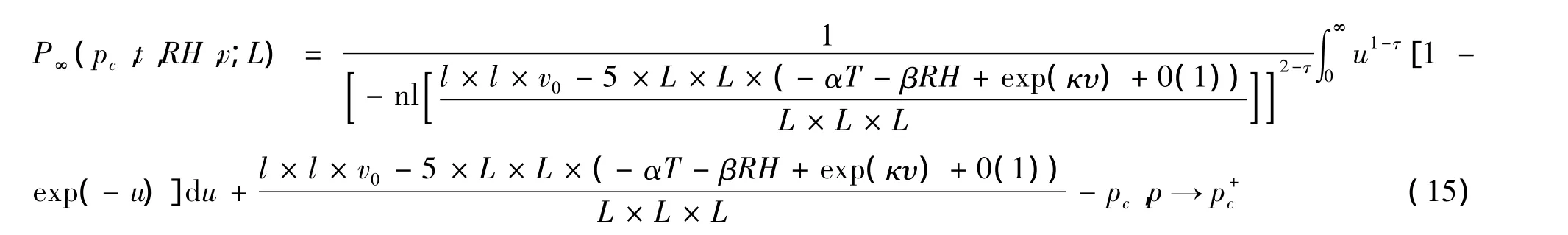
其对应的性质如图4所示.
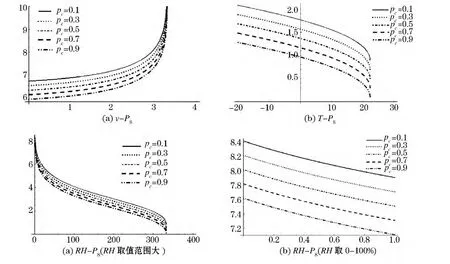
图4 P∞特征图(不同v的影响)
图4表示了P∞与温度、湿度以及风速的变化规律,其中纵坐标表示P∞,横坐标分别表示温度、湿度以及风速.其中的非线性表现的非常突出.(A)表示与风速之间的关系,(B)表示与温度之间的关系,(C)与(D)表示与空气湿度之间的关系,其中(A)表示当湿度取值范围很大时的非线性关系,但当湿度在0~100%取值时,表现为一条近似的直线,见图4(D).
P∞(p)描述了游离于聚集体数量外部的被污染了的大气粒子的数量,从图中可以看出,这一序参量受到温度、温度以及风速的影响非常的大,呈现出显著的非线性.并且随着风速的增大,这个量迅速增大,直至整个系统中的游离污染粒子迅速增多,结合图2、3,可以知道,在临界区域,整个大气系统中被污染的空气粒子呈现出级数级的缩减.而湿度与温度则表现出强烈的非线性影响,不过这种影响正好与风速的影响是相反的.
综上,图2~4所描述的结论与图1所给出的实际结果几乎完全一致,不仅表明这一模型是准确的,而且还可以看出,大气质量发生相变的临界点是存在的.进一步来说,在临界点上,一个微小的正ΔV加入,将非线性的造成空气质量的剧烈变差,这是由于排放总量与空气质量的关系是非线性的,故,排放结构中的量对空气质量的关系也是非线性的.因此,绝对不能用线性相加的办法去分析.
可见,即使空气粒子被均匀地“污染”,在其临界点上雾霾突然形成并增加.并且,这一均匀的污染取决于污染源的增长情况.也就是污染源中超过临界点的那些最终决定了系统的逾渗.换句话说,我们更应该关注烟尘的排放率增加率及其波动情况,而不是总体排放率.即使一种排放源尽管排放所占的比重很大,但是如果排放量稳定或递减,它一定不比那些排放比重少但增加幅度大的那些排放源关键.进一步而言,正是由于这一小部分排放源的增加使得整个污染源对大气的攻击超过逾渗的临界点,才使得整个系统从纯净的大气相转变到灰沉沉的雾霾相中.因此,我们说,这些因素在临界区域是关键因素.
3 结语
我国的大气状态处于雾霾逾渗的临界状态,在这一临界点上,废气排放的微弱变化也能形成较大的雾霾,这一点主要表现为雾霾与气象参数敏感性直接相关却并不是废气排放总量直接相关.在雾霾发生的过程中,存在一个超临界区,其实就是当污染废气排放达到雾霾逾渗的临界点时,会出现一种奇怪的现象,即使是排放量小于临界量,也会由于气象原因产生严重的雾霾,我们称之为超临界区.进一步来说,我国大气正处于临界与超临界的广义区域中.
在这一区域中,起决定性的废气排放因素并不是排放总量,而是排放量增长性波动最大的废气排放活动.根据调查,我们认为我国导致雾霾的关键因素是车辆废气排放,然后是工业排废气,并且前者更为重要.当然,在研究的过程中,新城镇化过程中产生的灰尘也是一个主要的原因,但在研究的过程中,我们难以收集到对应的数据,因此将这一因素给予忽略.
对于空气治理来说,应该是一个长期的工程,逐步改善整个排放情况,逐步改善生态环境,从而使得我们的大气远离临界点,得到一个完全清澈的空气.要达到这一目标,需要设置合理的治理机制并在实施过程中严格遵循,否则,我国大气会永远滞留于超临界区域.
[1]刘生丽,冯辉霞,张建强,等.逾渗理论的研究及应用进展[J].应用化工,2010,39(7):1074-1078.
[2]齐艳红,张文军.有害生物侵扰在多样化生境中的一种随机扩散过程及网络计算软件[J].现代计算机,2002,133(2):16-19.
[3]张小曳,孙俊英,王亚强,等.我国雾-霾成因及其治理的思考[J].科学通报,2013,58(13):1178-1187.
[4]徐 敬,丁国安,颜 鹏,等.北京地区PM2.5的成分特征及来源分析[J].应用气象学报,2007,18(5):645-654.
[5]王明珠,刘诗奇,石蜜蜜.北京PM2.5排放量估算及预测一一以秸秆燃烧为例[J].电子制作,2013,9:245,230.
[6]马丽梅,张 晓.中国雾霾污染的空间效应及经济、能源结构影响[J].中国工业经济,2014,4:19-31.
[7]陈 媛,岑 况,NORRA S,等.北京市区大气气溶胶PM2.5污染特征及颗粒物溯源与追踪分析[J].现代地质,2010,24(2):345-354.
[8]赵晨曦,王云琦,王玉杰,等.北京地区冬春PM2.5和PM10污染水平时空分布及其与气象条件的关系[J].环境科学,2014,35(2):418-427.
[9]邓利群,钱 骏,廖瑞雪.2009年8~9月成都市颗粒物污染及其与气象条件的关系[J].中国环境科学,2012,32(8):1433-1438.
[10]刘 强,李 平.大范围严重雾霾现象的成因分析与对策建议[J].中国社会科学院研究生院学报,2014,9:63-68.
[11]马先南.三维MANDELBROT渗流下临界形态[J].数学理论与应用,2007,27(3):30-33.
[12]CHENG J,DING R,LIU Y.Simulation on percolation of fractal aggregations[J].Chinese Journal of Computational Physics,2007,24(1):83-89.
[13]SU Z G.A lemma on AB-percolation models in high dimension[J].Journal of Zhejiang University(Sciences Edition),2000,27(6):682-688.

