基于MKSVM和MRF的高光谱影像分类方法

谭熊， 余旭初， 张鹏强， 付琼莹， 魏祥坡, 高猛

(1.信息工程大学，郑州 450001; 2.江西省数字国土重点实验室(东华理工大学)，南昌 330000)

基于MKSVM和MRF的高光谱影像分类方法

谭熊1,2， 余旭初1， 张鹏强1， 付琼莹1， 魏祥坡1, 高猛1

(1.信息工程大学，郑州 450001; 2.江西省数字国土重点实验室(东华理工大学)，南昌 330000)

为充分利用高光谱遥感影像中丰富的光谱和空间信息，提出了一种基于多核支持向量机(multiple kernel support vector machine,MKSVM)和马尔科夫随机场(markov random field,MRF)的影像分类方法。该方法首先利用MKSVM分类器对影像进行分类处理，再利用MRF对初始分类结果进行空间结构规则化，得到最终分类结果。通过对AVIRIS高光谱影像的分类实验表明,该方法有效地消除了分类结果中同质区域内的“噪声”，分类精度提高了3%左右。

高光谱影像；多核支持向量机(MKSVM)；马尔科夫随机场(MRF)；分类

0 引言

高光谱遥感是现代遥感技术发展的里程碑[1]。在过去30 a间，无论是成像光谱技术还是影像处理技术都得到了迅猛发展，取得了丰硕的研究成果。高光谱影像中包含丰富的光谱和空间特征信息，为更加有效地利用这2种信息，近年来国内外相关学者研究出了大量的高光谱影像分类方法，并根据分类处理过程中利用空间特征信息的方式和时机不同而分为2种类型：一是在分类过程中加入空间信息[2-3]；二是对分类结果进行空间结构规则化后处理[4-7]。这2种类型的分类方法均在一定程度上提高了分类精度。

但就分类器的选择而言，上述方法大多数是以有限样本条件下能够取得较好分类效果的支持向量机(support vector machine,SVM)方法为主，但SVM方法也存在着明显的不足[8]；另外，SVM是基于单个特征空间的单核方法，由于不同核函数或同一核函数不同参数具有不同的特性，当样本特征含有异构信息、样本规模较大或多维数据不规则时，采用单核映射方式对所有样本进行处理并不合理。针对这些问题，有关学者研究出了大量关于利用多核代替单核的学习方法，即多核学习方法[9]。多核学习方法不仅能够增强决策函数的能力，而且还能提高学习的性能，现已成为机器学习领域的研究热点之一。

由于高光谱影像具有数据量大、波段数多以及波段之间相关性大等特点，且影像中地物类型复杂多样，若将高光谱影像数据作为一个整体输入到只有单个核函数或单个参数的单核学习方法(以SVM为例)中，势必会对分类结果产生一定的影响。针对这些问题，广大专家学者正积极研究将多核学习方法用于高光谱影像分类处理中，且取得了一些初步成果[10-12]。但这些方法在模型选择和计算效率上存在一定的局限性，且没有有效利用高光谱影像中的空间特征信息。

马尔科夫随机场(markov random field,MRF)模型在描述高光谱影像相邻像元的相关性方面具有一定的优势，且在高光谱影像分类中应用较多。因此，本文将多核支持向量机(multiple kernel support vector machine,MKSVM)分类方法和MRF空间结构规则化后处理相结合，提出了一种基于MKSVM和MRF的高光谱影像分类方法，并通过AVIRIS高光谱影像实验，证明该方法的有效性。

1 方法原理

1.1 MKSVM分类

假定Km(x,z),(m=1,2,…,m)，是满足Mercer定理的核函数，则其加权组合核K(x,z)也是核函数，即

(1)

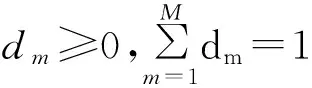
根据SVM算法的对偶问题，用组合核函数代替单核函数，可得MKSVM的对偶问题，即

(2)

式中:xi,xj为样本向量,i=1,2,…,n;yi,yj为类别标签;αi，αj为拉格朗日系数;C为惩罚系数。

式(2)为包含变量α和dm的凸优化问题，要得到其最优解,可分如下2个步骤进行解算：

第1步，解算最优解α*。式(2)的目标函数可看成是一个包含变量dm的标准SVM问题。因此，通过解算单个SVM问题得到包含dm的α的最优解为α*。

第2步，解算dm。在第1步的基础上，若α*与dm无关，则式(2)可表示为

(3)

式中J(dm)为包含最优解α*的目标函数。对于一个给定的dm，J(dm)对dm的微分(即梯度)为

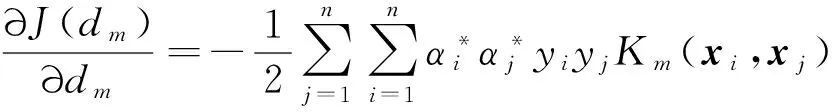
(4)

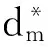
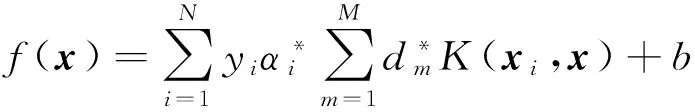
(5)

上述解算过程主要是针对2类分类问题。在MKSVM多类分类时，由于MKSVM是通过梯度下降法迭代解算单个SVM问题，可采用SVM的多类分类策略即一对一法(one against one,OAO)和一对余法(one against rest,OAR)进行多类分类。针对OAR分类策略，在得到MKSVM输出后，再采用Platt等[13]提出的利用Sigmoid函数将初始分类结果转化为两两配对的类后验概率，转换公式为

(6)

式中:f(x)为分类器输出函数; 参数A和B可从训练样本集中估计得出，也可根据经验值直接给出。为简单起见，本文中A和B的取值分别为-1和0。

1.2 MRF空间结构规则化

由马尔科夫随机场定义及其特性可知，图像中像元的连续分布表现在图像上像元对其邻域的依赖性，即图像全局对某像元状态的影响等价于该像元的邻域对其影响，高光谱影像亦如此。

根据最大后验概率马尔科夫随机场模型(MAP-MRF)理论，将高光谱影像MKSVM初始分类得到的后验概率通过

Uspectral(xi)=-ln[P(xi|yi)]

(7)

转化为光谱能量函数，并将其作为一部分与

(8)

的MRF空间能量函数结合，则在像元处形成的新能量函数可表示为

U(xi)=Uspectral(xi)+Uspatial(xi) 。

(9)

式(7)为高光谱影像的光谱能量函数，其中P(xi|yi)可通过式(6)计算得到；式(8)为局部邻域Ni内的空间能量函数，其中β为控制光谱或空间能量重要性的参数，δ(yi,yj)为Kronecker函数，其含义为当yi=yj时取值为1，当yi≠yj时取值为0。

MRF模型能量函数最小化的常用算法包括局部迭代条件模型(iterationconditionalmodel,ICM)、模拟退火算法(simulatedannealingalgorithm,SA)、遗传算法(geneticalgorithm,GA)、图割法(graphcut,GC)以及最大期望法(expectationmaximization,EM)等。由于ICM算法收敛速度快，计算效率高。因此本文采用ICM对式(9)的能量函数进行最小化处理。ICM算法的迭代过程如下：

第1步,根据式(7)和式(8)分别计算高光谱影像初始分类结果中每个像元的局部光谱能量函数和局部空间能量函数，再根据式(9)计算每个像元的局部新能量；

第2步,遍历初始分类结果图中所有的像元，并计算各像元能量之和，即全局能量U；

第3步,计算图像上所有类别对每个像元的局部能量，以局部能量最小的标号代替该像元的初始标号；

第4步,待所有像元标号调整后，重新计算全部能量U′；

第5步,当标号调整前后全局能量差值△U=|U′-U|小于某一阈值T时，迭代结束。

基于MKSVM和MRF的高光谱影像分类方法具体流程如图1所示。

图1 基于MKSVM和MRF的高光谱影像分类流程Fig.1 Flowchart of hyperspectral image classification based on MKSVM and MRF

2 实验与分析

为了检验本文分类器的性能，将基于MKSVM分类方法与本文方法进行比较分析。

2.1 基核函数选择

由于径向基核函数(RBF)和多项式核函数(POLY)在性能和分类效果上都明显优于其他核函数，因此本文主要选择这2种核函数作为基核函数进行实验，其表达式分别为

K(x,z)=exp(-‖x-z‖2/2σ2)

(10)

K(x,z)=(xz+1)p

(11)

式中：σ为高斯核参数；p为多项式系数。

在选定基本核函数后，多核函数的组合方式根据基本核函数参数的参与程度不同可以分为2类：一是同一核函数不同参数组成的多核函数；二是同一核函数的所有参数作为一个基核函数组成的多核函数。

2.2 参数的设置

在参数设置方面，MKSVM分类器不仅包含上述核函数参数，同时还包括惩罚系数C、权系数dm等，在分类时需要进行预先设置。在本实验中，σ的取值范围设置为{0.2,0.4,…,2.0}；p的取值范围为{1,2}；C的取值范围为{10-2,10-1,…,103}，经过5-折交叉验证，选择最佳的C为1 000；权系数dm的初始值设置为1/M(M为基核函数个数)，根据2.1节所述的多核组合方式，M取值分别为12和2；最大迭代次数为100次。

在MRF空间结构规则化的过程中，选用4邻域计算周围像元对中心像元的影响；β取值为0.5；全局能量差的阈值T设为0.05；最大迭代次数设为10次。

2.3 实验

实验数据采用美国喷气实验室(JPL)研制的AVIRIS成像光谱仪获取的印第安纳州西北地区的高光谱影像(Indian pines image)，该数据的光谱覆盖范围为400～2 500 nm，光谱分辨率为10 nm，影像大小为145像元×145像元，空间分辨率约为20 m，原始波段数为224个，去掉4个DN值为0的波段(分别为波段1,33,97和161),用剩余的220个波段进行分类实验。第47,27,17波段合成的假彩色图像和地面真实数据分别如图2(a)(b)所示，其类别和样本数量信息如表1所示。

(a) 假彩色合成图像(b) 地面真实数据

图2 AVIRIS假彩色合成图像和地面真实数据Fig.2 AVIRIS false color composite image and ground truth data

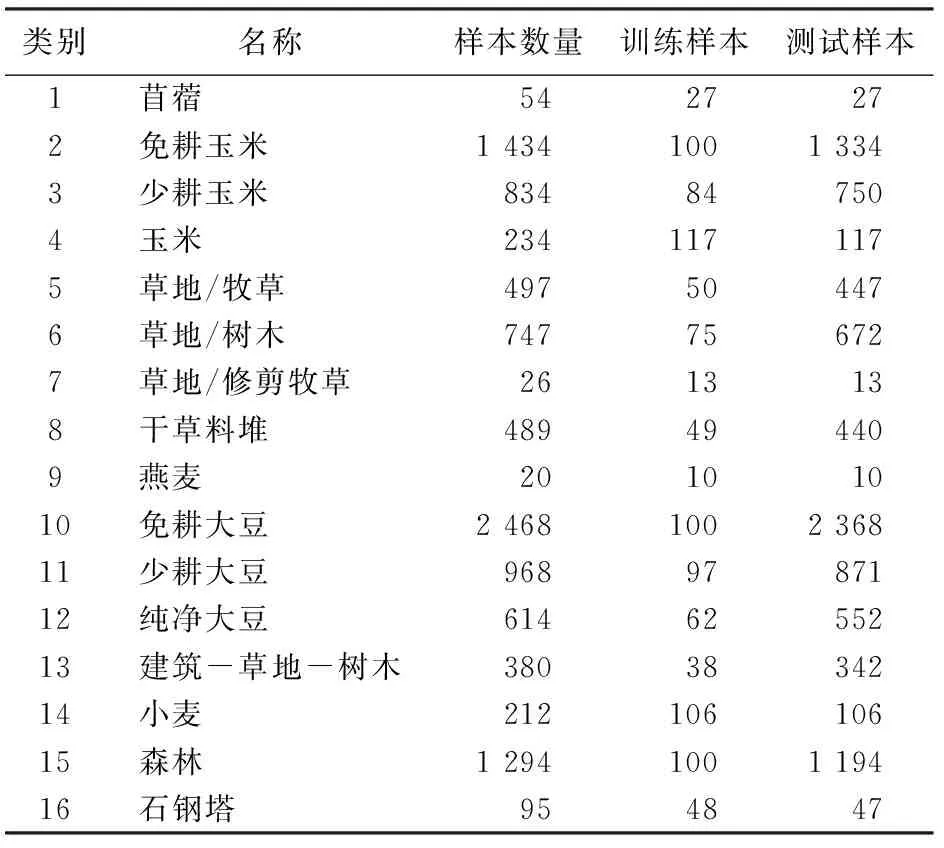
表1 AVIRIS影像样本信息Tab.1 AVIRIS image sample information

将AVIRIS影像的各类别样本随机地分成训练样本和测试样本(当某类别样本数量少于100时，取50%为训练样本，50%为测试样本；当样本数量多于100且少于1 000时，取10%为训练样本，余下的为测试样本；当样本数量大于1 000时，取100个为训练样本，余下的为测试样本)。训练样本用于分类器的学习训练; 测试样本用于分类精度的检测。在对该影像数据进行分类处理前，首先将数据的DN值归一化到[0,1]范围内。在实验中，采用不同的多核组合方式和多类分类构造策略，并与MKSVM分类方法进行对比分析，分类精度和Kappa系数如表2所示。

表2 不同分类方法精度对比Tab.2 Accuracy comparison of different classification methods (%)

①数字加粗部分表示分类精度或Kappa系数的最优值。

表2中Single表示用同一核函数不同参数作为基核函数的多核组合方式；All表示用同一核函数所有参数作为一个基核函数的多核组合方式；OAO表示迭代过程中单个支持向量机多类分类器的构造策略为“一对一”法；OAR表示“一对余”法。

利用本文方法和没有进行MRF空间结构规则化的MKSVM的分类结果如图3所示。图中分类结果所采用的多类分类器构造策略为“一对一”法，多核组合方式为同一核函数所有参数作为一个基核函数的多核组合方式。

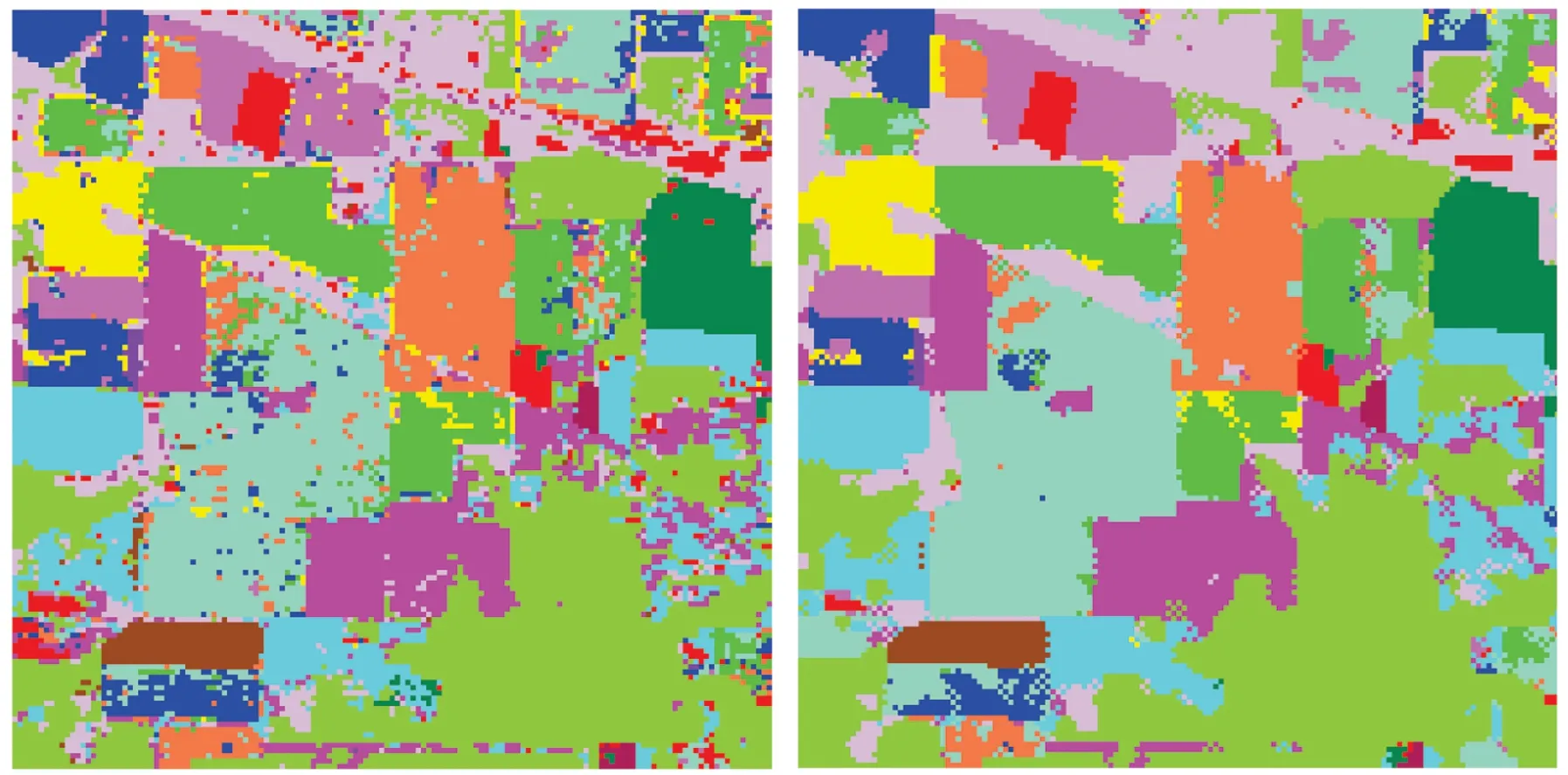
(a) MKSVM分类结果(b) MKSVM-MRF分类结果

图3 不同方法分类结果对比Fig.3 Comparison of different methods classification results

2.4 结果分析

综合分析图2(b)和图3可以看出，影像中所分地物类别基本正确。在图3(a)中，同质区域内夹杂着少量其他地物类别或随机噪声，主要表现为“麻点”现象；而本文MKSVM-MRF方法的分类结果(图3(b))有效地消除了同质区域内的“麻点”或噪声，得到了较好的分类结果：

1)在同一多核组合方式、同一SVM多类分类器构造策略的条件下，MKSVM-MRF方法的总体分类精度较MKSVM方法的提高了3%左右，Kappa系数也提高了3%以上；

2)16种不同地物类型的分类精度以MKSVM-MRF法(ALL-OAO和ALL-OAR)的多核组合方式最高；

3)在2种分类方法中，ALL-OAO和ALL-OAR的分类精度和Kappa系数明显高于同一核函数不同参数的多核组合方式(Single-OAO和Single-OAR)；

4)在2种分类方法中，“OAO”法多类分类器构造策略在分类精度和Kappa系数上优于“OAR”法。

3 结论

本文提出的基于MKSVM和MRF的高光谱影像分类方法主要由2个步骤完成：第一步利用MKSVM分类器对高光谱影像进行分类处理，得到地表覆盖的初始分类结果；第二步利用MRF对初始分类结果进行空间结构规则化，得到最终结果。采用AVIRIS成像光谱仪获取的美国印第安纳州西北地区的高光谱影像进行的实验结果表明：基于MKSVM和MRF的高光谱影像分类方法不仅有效地消除了分类结果中的噪声或“麻点”现象，而且还提高了分类精度。

[1] 余旭初,冯伍法,林丽霞.高光谱——遥感测绘的新机遇[J].测绘科学技术学报,2006,23(2):101-105. Yu X C,Feng W F,Lin L X.Hyperspectralmote sensing:A new opportunity for surveying and mapping[J].Journal of Geomatics Science and Technology,2006,23(2):101-105.

[2] Fauvel M,Benediktsson J A,Chanussot J.Spectral and spatial classification of hyperspectral data using SVMs and morphological profiles[J].IEEE Transactions on Geoscience and Remote Sensing,2008,46(11):3804-3814.

[3] 吴昊.综合纹理特征的高光谱遥感图像分类方法[J].计算机工程与设计,2012,33(5):1993-1996. Wu H.Classification methodology combined with texture feature for hyperspectral remote sensing image[J].Computer Engineering and Design,2012,33(5):1993-1996.

[4] Li C H,Kuo B C,Lin C T,et al.A spatial-contextual support vector machine for remotely sensed image classification[J].IEEE Transactions on Geoscience and Remote Sensing,2012,50(3):784-799.

[5] Tarabalka Y,Tilton J C,Benediktsson J A,et al.Marker-based Hierarchical Segmentation and Classification Approach for Hyperspectral Imagery[C]//ICASSP’11.Prague Congress Center.Prague,Czech Republic,2011:1089-1092.

[6] Tarabalka Y,Fauvel M,Chanussot J,et al.SVM and MRF based method for accurate classification of hyperspectral images[J].IEEE Transactions on Geoscience and Remote Sensing Letters,2010,7(4):736-740.

[7] Zhang B,Li S S,Jia X P,et al.Adaptive Markov random field approach for classification of hyperspectral imagery[J].IEEE Transactions on Geoscience and Remote Sensing Letters,2011,8(5):973-977.

[8] 杨国鹏,余旭初,周欣,等.基于相关向量机的高光谱影像分类研究[J].测绘学报,2010,39(6):572-578. Yang G P,Yu X C,Zhou X,et al.Research on relevance vector machine for hyperspectral imagery classification[J].Acta Geodaetica et Cartographica Sinica,2010,39(6):572-578.

[9] 汪洪桥,孙富春,蔡艳宁,等.多核学习方法[J].自动化学报,2010,36(8):1037-1050. Wang H Q,Sun F C,Cai Y N,et al.On multiple kernel learning methods[J].Aata Automatica Sinica,2010,36(8):1037-1050.

[10]尚坤,李培军,程涛.基于合成核支持向量机的高光谱土地覆盖分类[J].北京大学学报:自然科学版,2011,47(1):109-114. Shang K,Li P J,Cheng T.Land cover classification of hyperspectral data using composite kernel support vector machines[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2011,47(1):109-114.

[11]Gu Y F,Wang C,You D,et al.Representative multiple kernel learning for classification in hyperspectral imagery[J].IEEE Transactions on Geoscience and Remote Sensing,2012,50(7):2852-2865.

[12]谭熊,余旭初,秦进春,等.高光谱影像的多核SVM分类[J].仪器仪表学报,2014,35(2):405-411. Tan X,Yu X C,Qin J C.et al.Multiple kernel SVM classification for hyperspectral images[J].Chinese Journal of Scientific Instrument,2014,35(2):405-411.

[13]Platt J C.Probabilistic Outputs for Support Vector Machines and Comparisons to Regularized Likelihood Methods[OL].(1999).http://research.miscrosoft.com/～jplatt.

(责任编辑：刁淑娟)

Hyperspectral images classification based on MKSVM and MRF

TAN Xiong1, 2, YU Xuchu1, ZHANG Pengqiang1, FU Qiongying1, WEI Xiangpo1， GAO Meng1

(1.InformationEngineeringUniversity,Zhengzhou450001,China; 2.JiangxiProvinceKeyLabforDigitalLand,EastChinaInstituteofTechnology,Nanchang330000,China)

To fully utilize the spectral and spatial information rich in hyperspectral remote sensing images, this paper proposes a hyperspectral images classification method based on multiple kernel support vector machine (MKSVM) and Markov random field (MRF). Firstly, the MKSVM classifier is used to classify hyperspectral images, then the MRF is used to regularize the initial classification results in the spatial structure, and the final classification results are obtained in the end. The experiment on AVIRIS hyperspectral image shows that the proposed method not only effectively eliminates the “noise” in the homogeneous regions within the classification results but also improves the classification accuracy by about 3%.

hyperspectral images; multiple kernel support vector machine (MKSVM); Markov random field (MRF); classification

2014-05-10；

2014-07-25

国家自然科学基金青年科学基金项目“机载低空摄像机在线检校与视频影像实时处理技术研究”(编号：41201477)和江西省数字国土重点实验室开放基金项目“联合光谱/空间光谱信息的高光谱影像分类技术”(编号：DLLJ201403)共同资助。

10.6046/gtzyyg.2015.03.08

谭熊,余旭初,张鹏强,等.基于MKSVM和MRF的高光谱影像分类方法[J].国土资源遥感，2015，27(3)：42-46.(Tan X,Yu X C,Zhang P Q,et al.Hyperspectral images classification based on MKSVM and MRF[J] Remote Sensing for Land and Resources,2015，27(3)：42-46.)

TP 751

A

1001-070X(2015)03-0042-05

谭熊(1986-),男,讲师,主要研究方向为模式识别、高光谱影像处理与分析等。Email：kjadetx@163.com。