基于势函数点分布调整的SIFT图像配准算法

孙彬， 边辉， 王培忠

(西北核技术研究所,西安 710024)

基于势函数点分布调整的SIFT图像配准算法

孙彬， 边辉， 王培忠

(西北核技术研究所,西安 710024)

尺度不变特征转换(scale invariant feature transform，SIFT)是一种广泛应用于图像配准领域的点特征提取算法。针对基于SIFT的图像自动配准算法存在的特征点分布不均匀问题，提出了一种基于势函数点分布调整的图像配准方法。该方法解决了SIFT算法不能针对特征点的分布情况进行优化的问题。通过调整SIFT的比值阈值，增加配准点的数目；通过引入分子力学中的势函数概念，对特征点分布情况进行优化；通过局部互信息精纠正，微调特征点位置，以提高特征配准点的配准精度；最终实现高质量(空间分布均衡，配准精度高)的图像自动配准。

尺度不变特征转换(SIFT)；势函数；特征点分布；局部互信息

0 引言

图像配准是将不同时间、不同传感器(成像设备)或不同条件下(天候、照度、摄像位置和角度等)获取的2幅或多幅图像进行匹配、叠加的过程，已经被广泛地应用于遥感数据分析、计算机视觉、图像处理等领域。精确的图像配准能够为遥感调查与监测打下良好的基础[1-2]。基于特征的图像配准方法是研究较多且应用比较广泛的一类方法，这类方法的主要共同之处是先对角点、直线、轮廓及交叉点等图像特征进行提取，再完成图像特征之间的匹配，最后通过特征的匹配关系建立图像间的变换关系[3-4]。1988年，Harris和Stephens提出了Harris角点检测算法[5]；1997年，Smith和Brady提出了SUSAN(small univalue segment assimilating nucleus)角点检测法[6]；David等在1999年提出了尺度不变特征转换(scale invariant feature transform，SIFT)算子[7]，并在2004年对算法进行提升和总结，用于特征点的检测和描述。该算法一经被提出就引起了广泛关注，并成功应用到图像配准领域。对于基于点特征的图像自动配准算法，陈爱军等[8]指出配准点的选取方式直接决定了图像配准的有效性和可靠性，立体图像的配准精度并没有随配准点数量的增多而显著提高，但与这些配准点在图像上的几何分布有关[9]。为此，本文引入分子力学中的势函数概念，通过势函数对部分精度不高的特征点进行移动调整，优化了特征点的分布；通过提高特征点分布的均匀性，提高了图像的配准精度。

1 SIFT算法

SIFT算法是由David于1999年提出的[7]，该算法对尺度变化、视角变化、光照变换和噪声状况有很强的鲁棒性。国外学者针对不同条件下的图像配准，就SIFT、矩不变量及互相关等描述因子进行了实验和性能比较，结果证明SIFT算法的效果最好[10]。由图1可以看出，SIFT所提取的特征点在结构信息丰富的区域较为集中，但在A，B，C这3个影像特征相对平滑的区域却没有任何特征点存在。由此可见，单纯使用SIFT算法可能导致配准点分布均衡性较差。

图1 SIFT算法提取的特征点Fig.1 Feature points extracted by SIFT algorithm

2 基于势函数点分布调整算法

数学上的“点分布均匀”区域要满足3个要求：①区域内部的点越分散越好；②点离边界越远越好；③在低维投影上也需满足均匀性。胡东红等[11]根据势函数模型(potential function model)提出了一种基于势函数的均匀性度量准则；蔡文生等[12]提出的分子力学法则利用势函数来计算原子间的相互作用能，结合最优化算法使系统总势能最小化，用以预测复杂团簇的能量最低结构。同样，在图像配准领域,配准点分布也应遵循上述“点分布均匀”要求中的前2个，而基于势函数的点分布调整算法经数学证明能满足图像配准的上述要求[13]。

根据势函数模型的定义可以推导点分布均匀性调整的算法。点的受力总和可表示为

(1)

式中：Fi,j的大小和符号代表了点xi受其他点的作用之和在ej轴上的大小和方向；i，k为特征点索引(i,k=1,2,…,n)；j为空间维度索引(本文特指x,y轴方向(j=1,2,…,m))；s为平面延拓索引，对于矩形，需要在周边延拓8个平面(图2)。

图2 势函数计算延拓范围示意图Fig.2 Sketch map for scale of potential

对于所有的i和j，根据Fi,j的大小和符号，按一定策略移动点xi，直到Fi,j小于某一个阈值，即可认为达到均匀性要求。在二维空间上简化的基于势函数点分布调整算法(点按照Fi,j的大小和方向移动)如图3所示。

图3 基于势函数点分布调整的流程图Fig.3 Flowchart of point-adjust algorithm based on potential function

图4为点分布调整的仿真试验结果。

图4 点分布调整的试验结果

从表1可以看出，点分布调整前后势函数值的变化，说明点分布的均匀性得到了有效提高。

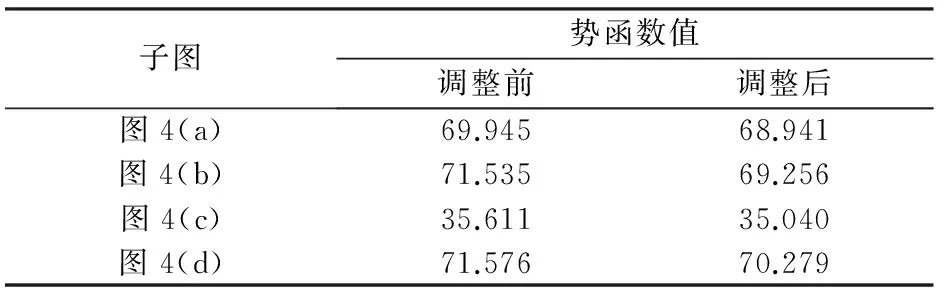
表1 点分布调整前后的势函数值Tab.1 Potential function values before and after adjusting point distribution

3 基于互信息的配准点偏差补偿

由于使用势函数模型对部分特征点进行了移动(图4)，使特征点的位置发生了改变，原有的配准关系被破坏。所以，需要对新的位置上的特征点使用原来粗配准变换矩阵进行映射；但这种通过映射得到的配准点对粗配准矩阵修正并没有起任何作用。为了提高配准点的精度，本文使用归一化互信息对移动过的配准点进行纠正，将配准点与对应的待配准图像进行局部归一化互信息偏差补偿。

将基准图像按照粗配准矩阵进行前向映射，需要将纠正点A(x,y)映射为AT(xT,yT)，并以AT为圆心在基准图像中取半径为r的圆形区域UA，如图5(b)所示；将A点对应在浮动点图像上的A′点的坐标(x′,y′)，取阈值t，设B点坐标(xb,yb)在区域T(xb∈[x′-t,x′+t],yb∈[y′-t,y′+t])内移动，以B点为圆心在浮动图像中取半径为r的圆形区域UB，如图5(c)所示；再计算UA与UB的归一化互信息，如果某个B点的UB与UA的互信息最大，则认为2个区域配准良好，AT与B为高精度配准点；如果该最大值小于一定的阈值，则认为无法正确配准。

(a) 基础图像 (b) 按粗匹配矩阵映射图像 (c) 待配准图像

图5 基于归一化互信息的纠正方法示意图

Fig.5 Adjusting based on normalized mutual information

利用该方法可以较好地提高配准点的精度；如果将选取的区域插值到原来图像的3～5倍时，则效果更好。配准点偏差补偿实验效果如图6所示。可以看出，特征点提取的偏差得到了很好的纠正。

(a) 基础图像 (b) SIFT配准结果(c) 互信息纠正结果

图6 基于归一化互信息的纠正效果

Fig.6 Effects of adjusting based on normalized mutual information

4 基于势函数点分布调整的SIFT算法

在上述算法的支持下，可对SIFT算法的特征点分布均匀性进行改进：首先使用SIFT算法提取特征点，并取较小的比值阈值，获得粗配准模型；然后使用势函数模型调整定位准确性较差的点位置，并使用粗配准模型进行映射；最后使用局部互信息进行精定位，即可得到定位精度高和均匀性好的控制点。具体的算法配准步骤如下：

1)分别提取参考图像和待配准图像的SIFT特征。

2)特征点之间的相似性采用欧氏距离度量，按照Lowe的研究结果，阈值取0.6～0.7之间；本文算法取0.4～0.5之间值，主要用于降低初配准精度、增加配准点数量。

3)进行随机抽样一致性(random sample consensus，RANSAC)检验，如果不能得到稳定的配准点对，则配准失败；否则，配准成功。

4)通过获得的配准点对计算仿射矩阵A，提高配准过程的比值阈值(取0.8～0.9之间)；通过A进行配准点筛选，可获得大量配准点。

5)按照上文所述基于势函数的点分布调整算法，将部分定位精度差的点重新调整，并按照仿射矩阵A进行重新映射。

6)使用互信息对重新调整过的点进行精确定位，若该点互信息值小于某个阈值，则剔除该点。

7)使用保留下来的配准点采用多项式法或者三角格网法进行图像配准。

5 实验结果与分析

针对图像的配准精度，本文给出3种常用的评价指标[14-15]：①均方根误差(root-mean-squared error，RMSE)；②平均绝对误差(mean absolute difference，MAD)；③配准图像相容性检测系数(entropy correlated coefficient，ECC)。

采用Matlab语言编写程序，测试平台为Win7 X64，CPU为X5675(3.06 GHz，6核)×2，内存为12 GB的图形工作站。图7给出使用本文算法与SIFT算法对不同传感器、不同获取时间、尺度区别较大的2景图像(2007年5月获取的某区域QuickBird图像(图7(a)，分辨率0.6 m，图像大小1 159像元×1 105像元)和2002年8月获取的SPOT5图像(图7(b)，分辨率2.5 m，图像大小648像元×677像元))的配准结果(图7(c)和图7(d))。

(a) 基础图像(QuickBird) (b) 待配准图像(SPOT5)

(c) SIFT算法结果 (d) 本文算法结果

图7 第一组图像配准实验结果

Fig.7 Registration experimental results of first group of remote sensing images

图8给出使用本文算法与SIFT算法对相同传感器、不同获取时间的2景某区域QuickBird图像(分别于2004年1月(图8(a)，图像大小477像元×475像元)和2005年2月获取(图8(b)，图像大小537像元×547像元))的配准结果(图8(c)和图8(d))。

(a) 基础图像(QuickBird) (b) 待配准图像

图8-1 第二组图像配准实验结果

Fig.8-1 Registration experimental results of second group of remote sensing images

(c) SIFT算法结果(d) 本文算法结果

图8-2 第二组图像配准实验结果

Fig.8-2 Registration experimental results of second group of remote sensing images

本文选取的上述2组图像具有一定的典型性和代表性。第一组图像为不同卫星、不同分辨率及不同获取时间的图像，特征点较为稀少。与SIFT算法相比，本文算法特征点数量明显增加，同时在原SIFT算法特征点比较稀疏的图像中部增加了部分特征配准点，使特征配准点分布的均匀性得到了有效提高(图7(d))。第二组图像为同一卫星、相同分辨率及不同获取时间的图像，特征点较为稠密，且分布不均匀；由于场地目标发生了较大的变化，本文算法比SIFT算法在配准点数量和特征点分布的均匀性上都得到了较大提高(图8(d))。

第一、二组的实验结果如表2所示。

表2 图像配准实验结果数据Tab.2 Data of registration experimental results of images

从表2可以看出，本文算法的RMSE，MAD及ECC等精度评价指标均比SIFT算法有较大的提升。但由于算法中采用势函数对点分布进行调整以及互信息计算会导致算法复杂度上升，故本文算法耗时较长。

6 结论

1)本文以尺度不变特征转换(SIFT)算法为基础，通过二次配准得到较多数目的控制点；并引入分子动力学中的势函数模型对SIFT算法进行改进，优化了SIFT算法的特征点分布，解决了SIFT算法特征点分布不均匀的问题；同时利用局部互信息提高了配准点对的精度；通过对特征点分布的调整，提高了图像的配准精度。

2)实验结果表明，本文算法具有较高精度，但由于算法中采用势函数对点分布进行调整以及互信息计算，导致算法复杂度上升，算法耗时较长。因此，该方法对于精度要求较高而时效性要求较低的应用领域具有较强的应用价值，并已成功地应用于卫星图像自动传输链路接收系统中。

[1] 张云生,邹峥嵘.基于改进ORB算法的遥感图像自动配准方法[J].国土资源遥感,2013,25(3):20-24.doi:10.6046/gtzyyg.2013.03.04. Zhang Y S,Zou Z R.Automatic registration method for remote sensing images based on improved ORB algorithm[J].Remote Sensing for Land and Resources,2013,25(3):20-24.doi:10.6046/gtzyyg.2013.03.04.

[2] 王晓华,邓喀中,杨化超.集成互补不变特征的SAR影像自动配准[J].国土资源遥感,2014,26(1)：52-56.doi:10.6046/gtzyyg.2014.01.10. Wang X H,Deng K Z,Yang H C.Automatic SAR image registration of integrated complementary invariant feature[J].Remote Sensing for Land and Resources,2014,26(1):52-56.doi:10.6046/gtzyyg.2014.01.10.

[3] 吴伟交,王敏,黄心汉,等.基于向量夹角的SIFT特征点匹配算法[J].模式识别与人工智能,2013,26(1):123-127. Wu W J,Wang M,Huang X H,et al.SIFT feature matching algorithm based on vector angle[J].Pattern Recognition and Artificial Intelligence,2013,26(1):123-127.

[4] 张谦,贾永红,胡忠文.多源遥感影像配准中的SIFT特征匹配改进[J].武汉大学学报：信息科学版,2013,38(4):456-459. Zhang Q,Jia Y H,Hu Z W.An improved SIFT algorithm for multi-source remote sensing image registration[J].Geomativs and Information Science of Wuhan University,2013,38(4):456-459.

[5] Harris C G,Stephens M J.A combined corner and edge etector[C]//Proc Fourth Alvey Vision Conference,Manchester,U K,1988.

[6] Smith S M,Brady J M.SUSAN-A new approach to low level image processing[J].International Journal of Computer Vision,1997(1):45-78.

[7] David G L.Object recognition from local scale-invariant features[C]//Proceedings of the International Conference on Computer Vision,Corfu:1999.

[8] 陈爱军,徐光祐,史元春,基于城市航空立体像对的全自动3维建筑物建模[J].测绘学报,2002,31(1):55-57. Chen A J,Xu G Y,Shi Y C.Automated 3D building modeling based on urban aerial stereopair[J].Acta Geodaetica et Cartographic Sinica,2002,31(1):55-57.

[9] Jonathan H.SPOT digital elvation model(DEM)creation using the Otto and Chau Method[DB/OL].[2004-09]http://www.jon-claudi.co.uk/ee/index.php/geofiction/extended_text/spot_digital_elevation_model_dem_cration_using_the_otto_and_chau_method/.

[10]Mikolajczyk K,Schmid C.Scale and affine invariant interest point detectors[J].International Journal of Computer Vision,2004,60(1):63-86.

[11]胡东红,李德华,王祖喜.均匀性度量的势函数模型[J].数学物理学报,2003,23,A(5):607-612. Hu D H,Li D H,Wang Z X.Potential function model of uniformity measurement[J].Acta Mathematiea Scientia,2003,23,A(5):607-612.

[12]蔡文生,林翼,邵学广.团簇研究中的原子间势函数[J].化学进展,2005,17(4):588-594. Cai W S,Lin Y,Shao X G.Interatomic potential function in cluster research[J].Progress In Chemistry,2005,17(4):588-594.

[13]张玲,张胜兰,艾君,等.基于势函数的均匀性度量与均匀性布点方法[J].湖北大学学报：自然科学版,2007,29(6):144-146. Zhang L,Zhang S L,Ai J,et al.Uniform measurement and uniform dots distribution based on potential function[J].Journal of Hubei University(Natural Science),2007,29(6):144-146.

[14]孙彬,严卫东,张彤,等.良分布的多特征遥感图像自动配准算法[J].光电工程,2012,39(8):38-45. Sun B,Yan W D,Zhang T,et al.Remote sensing image automated registration algorithm based on multi-feature and well-distribution[J].Opto-Electronic Engineering,2012,39(8):38-45.

[15]李伟峰,周金强,方胜辉.基于改进Hausdroff距离的图像配准方法[J].国土资源遥感,2014,26(2)：93-98.doi:10.6046/gtzyyg.2014.02.16. Li W F,Zhou J Q,Fang S H.Image registration method based on improved Hausdorff distance[J].Remote Sensing for Land and Resources,2014,26(2):93-98.doi:10.6046/gtzyyg.2014.02.16.

(责任编辑：刁淑娟)

Image registration algorithm based on SIFT and potential function adjusting location of points

SUN Bin, BIAN Hui, WANG Peizhong

(NorthwestInstituteofNuclearTechnology，Xi’an710024,China)

Scale invariant feature transform(SIFT) is a popular feature extraction algorithm that has applied to remote sensing image automatic registration; nevertheless, there exists a problem in the remote sensing image automatic registration based on SIFT algorithm, i.e., the distribution of feature points is always nonuniform. An automatic image registration algorithm based on potential function model is presented in this paper, which can solve the problem of optimizing nonuniformity in feature point distribution in SIFT. By adjusting the threshold of SIFT, the number of matching points is promoted. The algorithm can optimize the uniformity in feature point distribution by potential model function in molecular mechanics, and make the low-precision feature point to the sparse area of feature points. Then it revises local mutual information to improve matching point accuracy, so as to realize a high quality (uniform space distribution, high accuracy of Sub-Pixel registration) automatic image registration finally.

scale invariant feature transform (SIFT)；potential function；feature point distribution；local mutual information

2014-05-12；

2014-07-16

10.6046/gtzyyg.2015.03.07

孙彬,边辉,王培忠.基于势函数点分布调整的SIFT图像配准算法[J].国土资源遥感,2015,27(3)：36-41.(Sun B,Bian H,Wang P Z.Image registration algorithm based on SIFT and potential function adjusting location of points[J].Remote Sensing for Land and Resources,2015,27(3)：36-41.)

TP 751.1; TP 391.41

A

1001-070X(2015)03-0036-06

孙彬(1983-),男,硕士,工程师,主要从事遥感图像处理和图像配准技术研究。Email：sunbin@ninit.ac.cn。