某伸展臂锁定机构的可靠性分析

檀中强，邓国兵，赵明岩

(1.中国计量学院机电工程学院，浙江杭州 310018;2.浙江理工大学机械与自动控制学院，浙江杭州 310018;3.山东科瑞控股集团有限公司，山东东营 257000)

某伸展臂锁定机构的可靠性分析

檀中强1，2，邓国兵3，赵明岩1

(1.中国计量学院机电工程学院，浙江杭州 310018;2.浙江理工大学机械与自动控制学院，浙江杭州 310018;3.山东科瑞控股集团有限公司，山东东营 257000)

改进某伸展臂锁定机构，通过分析其工作原理与失效模式，构建锁定可靠性模型。综合考虑尺寸、装配误差和构件变形对锁定功能的影响，利用一次二阶矩法得到可靠性指标。结合实际尺寸，计算出室温及空间极限温度下的可靠度，分析出影响可靠度的主要因素，并提出改进措施。结果表明，新结构可有效提高可靠度。

伸展臂;锁定机构;机构运动精度可靠性

0 前言

伸展臂已应用在各种空间探测活动中［1－2］。作为其关键组成部分，锁定机构在伸展臂完全展开后，实现定位锁紧。锁定机构能否正常工作直接影响到伸展臂展开后的姿态稳定性［3］，甚至空间探测活动的成败。为确保伸展臂在工作中能够按要求到位锁紧，必须对其工作可靠性进行研究。文中分2个方面对锁定机构可靠性进行分析:(1)机构受加工和装配误差影响的锁定可靠性［4－5］;(2)机构受工作环境影响的锁定可靠性［6－7］。该研究对伸展臂展开到位锁定的高可靠性具有重要意义。

1 锁定机构工作原理

某伸展臂锁定机构经改进后，将销孔基体的尺寸增大，使挡块与销孔基体接触，这样加工后更容易装配，且能降低装配误差。改进后锁定机构的工作原理如图1所示，伸展臂完全展开后，定位件被筒壁上的挡块挡住，此时滑槽与销孔相对，如图1中位置。

图1 锁定机构锁紧原理示意图

驱动件继续向上运动，压缩伸缩连杆，锁紧滑销受力在滑槽中滑动。直到锁紧滑销进入销孔并压紧，锁定机构实现锁紧。

2 锁定机构可靠性分析

2.1 锁定机构失效模式分析

图2 锁紧滑销与销孔轴线位置

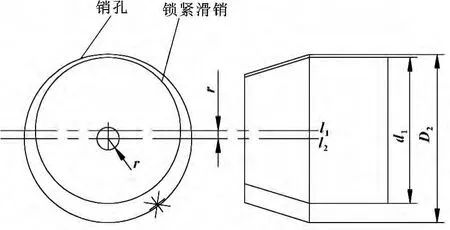
图3 限位锁定可靠

2.2 安全边界方程

从图1可以看出，当限位锁定机构的定位件被挡块挡住定位以后，滑销轴线与销孔轴线之间的距离r由锁紧滑销大端直径d1、滑槽直径D1、定位件的长度b、销孔轴线与挡块的距离a、及牵连运动引起的误差Δ牵等因素共同决定。

滑销能在滑槽中滑动，存在一定的尺寸间隙，以r1表示滑销轴线到滑槽上边缘的距离，则r、r1、b、a 4个尺寸形成一个与装配尺寸链类似的尺寸关系，如图4所示。

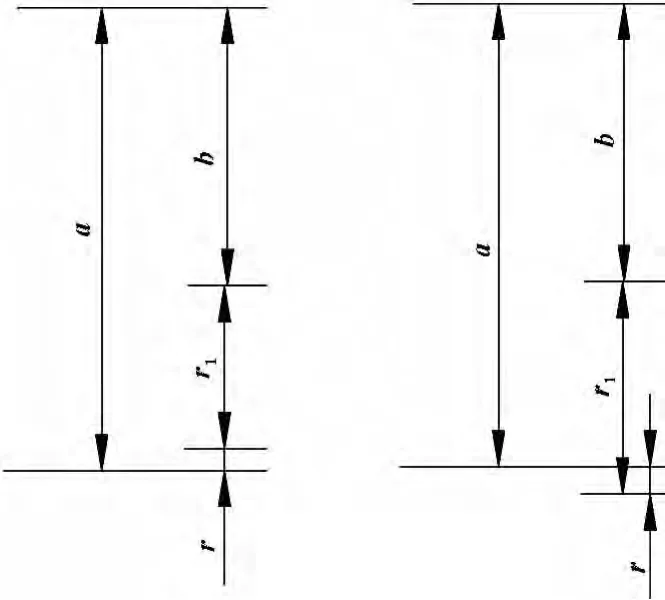
图4 装配尺寸链

故得销轴与销孔轴线之间的距离r为:

2.3 锁定机构的可靠性模型

2.3.1 加工装配误差对锁定机构可靠性的影响［8－10］

当考虑加工误差和装配误差的影响时，r1、b、a、D2、d1均可视为随机变量，且相互独立，假设各随机变量均服从正态分布，根据式 (5)可求出功能函数Z的均值和方差分别为:

式 (6)、(7)中，μx为随进变量x的均值，σx为随机变量x的均方差，x代指以上各随机变量。用可靠性分析一次二阶矩法得可靠性系数为:

2.3.2 构件变形对锁定机构可靠性的影响［11－12］

限位挡块可以近似为一个悬臂梁，在受到定位件给他的作用力后会发生一定量的变形而引起a的变化，以Δa表示。定位件受力，从而引起长度b的变化，以Δb1表示。受太空环境的影响，温度荷载使定位件发生变形，以Δb2表示。

销孔基体也会发生变形，定位件与销孔基体产生的变形在尺寸链中可以部分抵消，剩余量以Δb2的一半进行估算。则式 (2)改写为:

将以上两式代入式 (8)、(9)，可得考虑构件变形下的机构可靠度。

2.4 r1的均值与方差

3 锁定机构的可靠度计算

某伸展臂的参数选择原则:锁紧滑销在滑槽中运动，配合选择H7/g6，间隙很小，满足自由滑动且精密定位要求。故与孔有关的尺寸选择7级精度，与轴有关的尺寸选择6级精度。

4 改进措施

通过以上分析可知，将锁定机构改进后 (销孔基体顶住挡块)，温度变化对可靠度的影响已降低，但低温极限对机构正常锁定的影响仍不容忽视。为了消除温度对机构锁定可靠度的影响，由公式(13)可知，只要在设计时尽量减小b的尺寸即可，如图5(a)所示。如果结构尺寸允许，甚至可以修改限位挡块的位置，用销孔基体本身充当限位挡块，如图5(b)所示，此时b=0，温度的影响可以完全消除。

如果结构尺寸不允许，或者b的尺寸不能减小，还可以通过选择热线性系数小的材料、减小挡块长度以及提高加工精度等措施来提高可靠度。

图5 锁定机构改进图

5 结束语

文中对伸展臂锁定机构的可靠性进行了分析。当不考虑构件的变形时，加工及装配精度可保证其具有较高的锁定可靠度;当考虑构件变形时，低温极限温度对锁定机构工作可靠度的影响较大。通过对影响因素的具体分析，提出了相应的改进措施。文中对其他尺寸链的装配可靠性分析具有一定的借鉴作用。

［1］MIURA K，FURUYA H，SUZUKI K.Variable Geometry Truss and Its Application to Deployable Truss and Space Crane Arm［J］.Acta Astronautica，1985，12(7/8):599－607.

［2］KWAN A SK.A Pantographic Deployable Mast［D］.UK:University of Cambridge，1991.

［3］金恂叔.航天器环境试验和航天产品的质量与可靠性保证［J］.中国空间科学技术，2004(12):25－31.

［4］H.P.勃鲁也维奇.机构精确度［M］.上海:上海科学技术出版社，1966.

［5］LEE SJ，GILMORE B J.The Determination of the Probabilistic Properties of Velocities＆Accelerations in Kinematic Chains with Uncertainty［J］.Transactions of the ASME，1991，113(3):84 －90.

［6］HARDAWAY L M R，PETERSON L D.Nanometer Scale Spontaneous Vibrations in a Deployable Truss under Mechanical Loading［J］.American Institute of Aeronautics and Astronautics，2002，40(10):2070 －2076.

［7］LEVINE MAEIE B.The Interferometry Program Flight Experiments:IPEX I＆II［C］.Proceedings of SPIE Astronomical Telescopes and Instrumentation Conference.1998，Paper 3350－14:776－784.

［8］冯元生.机构可靠性理论的研究［J］.中国机械工程，1992，3(3):1 －3.

［9］刘惟信.机构可靠性设计［M］.北京:清华大学出版社，1996.

［10］陈建军，陈勇.平面四连杆机构运动精度可靠性分析与数字仿真［J］.西安电子科技大学学报，2001，28(6):759－763.

［11］北京科技大学，东北大学.工程力学［M］.北京:高等出版社，1997.

［12］徐芝纶.弹性力学［M］.北京:高等出版社，2006.

Reliability Analysis of Locking Mechanism of a Dep loyable Mast

TAN Zhongqiang1，2，DENG Guobing3，ZHAO Mingyan1
(1.College of Mechanical and Electrical Engineering，China Jiliang University，Hangzhou Zhejiang 310018，China;2.College of Machinery and Automatic Control，Zhejiang Sci-Tech University，Hangzhou Zhejiang 310018，China;3.Kerui Group，Dongying Shandong 257000，China)

Lockingmechanism of a deployablemastwasmodified.On the base of working principle，themechanism’s failure mode was analyzed and a new model of reliability was constructed.In the process of calculating reliability index，the factors such as size，assembly error，and space environment influence were taken into consideration，and the method of MFOSM(Mean First Order Second Moment)was applied.Based on the actual size of themechanism，locking reliabilities atboth room temperature and space limit temperature were calculated.Themain factors that influence the reliability were analyzed and the improvementwas put forward.The result shows that the new model has a high reliability.

Deployablemast;Lockingmechanism;Reliability ofmechanism kinematics accuracy

TH115

A

1001－3881(2015)21－197－4

10.3969/j.issn.1001 －3881.2015.21.049

2014－08－11

机械设计及理论浙江省重中之重学科和浙江理工大学重点实验室开放基金资助项目 (ZSTUMD2012A009)

檀中强 (1979—)，男，博士研究生，实验师，主要从事机构运动可靠性方向的研究。E－mail:tzq@cjlu.edu.cn。