一种组合并联机构的运动学分析及刚度分析
槐创锋,陈华,刘平安,舒迎将
(华东交通大学机电学院,江西南昌 330013)
一种组合并联机构的运动学分析及刚度分析
槐创锋,陈华,刘平安,舒迎将
(华东交通大学机电学院,江西南昌 330013)
以一种新型的可实现3-PUU机构和3-UPU机构的组合并联机构为对象,对该机构在可实现两种并联机构的情况下分别进行机构自由度分析、运动学分析,得出机构的运动学正逆解以及雅克比矩阵,根据所求出的雅克比矩阵进一步对机构进行机构刚度分析,并用MATLAB软件求解刚度值,绘制出在给定的位姿时上下平台的相关结构参数对整体刚度值的影响曲线图,为此组合并联机构的进一步分析提供了理论分析的依据,对组合并联机构的设计具有一定指导作用。
组合并联机构;运动学;雅可比矩阵;刚度分析
0 前言
并联机构在工作进程中总会承受外力载荷,即其末端执行器会对被作用的物体施加力或力矩的作用,如果并联机构的整体刚度较小,就会发生较大变形,导致其无法进行正常的工作,因而分析并联机构的刚度对于机构性能研究具有重要的理论价值和意义[1]。
至今已有不少学者对并联机构的刚度进行过分析,其中韩书葵等[2]采用螺旋理论方法推导出了少自由度机构刚度计算公式,分析了机构条件数,给出了机构最大刚度与最小刚度的计算方法,绘出了机构最大刚度和最小刚度曲线;孟巧玲[3]采用基于新的守恒协调刚度矩阵推导出3-PRR平面并联机构、6-SPS空间并联机构刚度映射公式,结合其工作空间对所研究的机构进行刚度特性分析;乐林林等[4]从动平台所受作用力和发生位移的关系角度,建立了刚度模型,并给出了机构静刚度的度量指标;胡波等人[5]在建立的刚度模型中考虑了约束反力对机构刚度的影响,能够体现约束对机构刚度的影响。可以看出,关于机构结构参数对机构刚度的影响还鲜有研究,本文作者从影响并联机构刚度的机构结构参数入手,研究一种可实现3自由度宏观运动和3自由度微动调节的3PUPU的医疗并联机构[6]的刚度随机构结构参数变化情况。先分别对处于两种结构状态时的并联机构的进行运动学分析,得出机构运动正逆解,并计算出机构的雅克比矩阵;其次,通过得出的雅克比矩阵分析机构的整体刚度值随上下平台结构参数的变化情况;最后,应用MATLAB软件对整体刚度值进行运算分析,并绘制出上下平台结构参数对整体刚度的影响曲面图。根据影响曲面图,得出机构整体刚度是否受上下平台结构参数的影响,如果有影响,可以对所设计的并联机构结构尺寸进行适当的修正,使之能够获得较高的刚度,进而保证机构能够顺利圆满地完成每一个工作任务。
1 3-PUPU并联机构
如图1所示,该装置利用3-UPU和3-PUU两种3自由度并联机构支链运动副组成相近的特点,将两种并联机构支链中的“PU”部分支链进行共用,组成了一种能够实现3自由度宏观运动和3自由度微动调节的3PUPU的医疗并联机器人。它是一种部分支链重合的组合并联机构,通过部分驱动运动副锁死和放开实现可用于医疗机器人的位置和姿态控制,能够实现宏观运动和微动调节两种复合运动形式的场合。

图1 3-PUPU并联机构总装配示意图
2 机构运动学分析
2.1 机构作为3-UPU并联机构实现运动输出
要实现三自由度3-UPU并联机构运动输出时,锁死滑块9、10、11,将机构简化如图2所示。其中动静平台通过3条UPU支链连接在一起,P副作为驱动副,U副为从动副,而且分别与动静平台相连的两个转动副轴线相互平行,并共同平行于动静平台,P副两端的两个转动副轴线也是相互平行的。在动静平台上分别建立oxyz和OXYZ空间直角坐标系,初始位置时,Z轴和z轴均垂直于动静平台,Y轴与$i1重合,y轴与$i5重合。
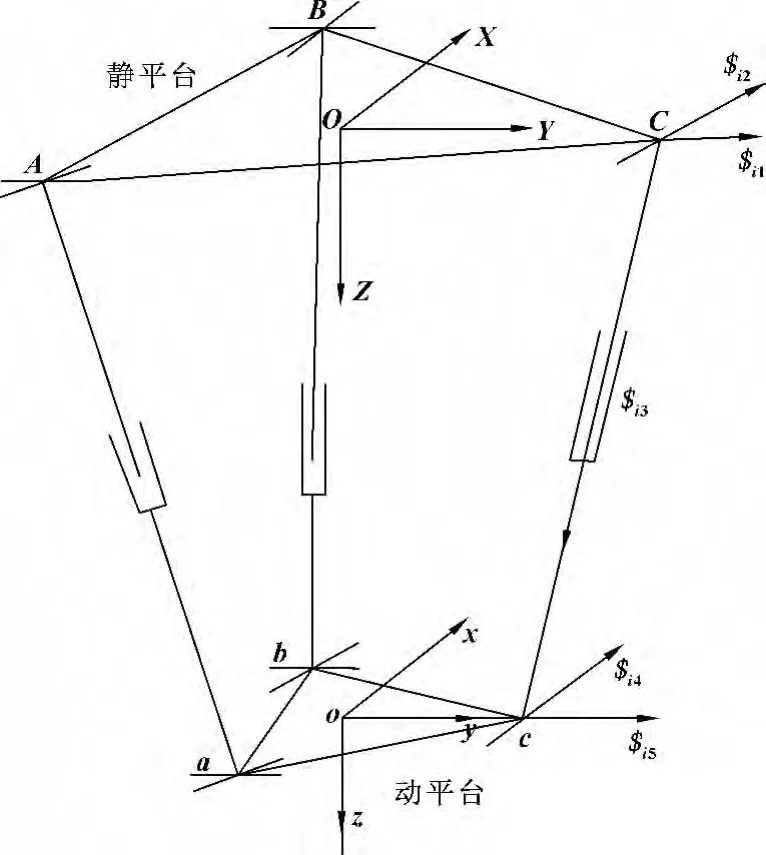
图2 3-UPU并联机构示意图
2.1.1 计算3-UPU并联机构的自由度
运用螺旋理论,求出第i条分支的分支运动螺旋系如下:

利用分支运动螺旋和分支约束螺旋相逆的原理,由分支运动螺旋可以推导出第i条分支的分支约束螺旋系,如下:

由式 (1)可知,3-UPU并联机构的每个UPU分支链对动平台都会施加1个平行于基座标系Z轴方向的约束力偶,由于静平台基座标系的X、Y轴分别与静平台相连的万向铰两个轴线平行,这个约束力偶一定会垂直于与静平台相连的万向铰两个轴线所在平面,而且静平台处相连的3个万向铰轴线所在平面均不平行也不重合,故3个约束力偶也互不平行,因此,3个约束力偶将会约束动平台的3个转动,此3-UPU并联机构拥有3个移动自由度。
2.1.2 作为3-UPU并联机构时的位置逆解的计算
并联机构的位置反解指已知输出参数求输入参数,如图2所示,设动静平台各个虎克铰的中心点的连线分别为两个相似的等边三角形△abc和△ABC,其边长分别为d和D,且 Aa=L1,Bb=L2,Cc=L3,动平台的中心点o在静平台坐标系OXYZ中的坐标为Oo=(x y z),可列出如下方程组:位形,两种情况均有


2.2 机构作为3-PUU并联机构实现运动输出
如前文所述,要实现三自由度3-PUU并联机构运动输出时,锁死直线驱动器16、17、18,滑块1、滑块2和滑块3为该机构的驱动装置,3-PUU机构简图如图3所示,此时,动静平台通过3条PUU支链连接在一起,P副作为驱动副,U副为从动副,而且分别与动静平台相连的转动副轴线对应相互平行,并共同平行于动静平台。在动静平台上分别建立oxyz和OXYZ空间直角坐标系,Y轴与$i3平行,X轴与$i2平行,且$i2与$i4平行,$i3与$i5平行。
由式 (8)可知,3-UPU并联机构在D=d时,即上下平台为全等的等边三角形时,处于奇异位形状态,这时3条UPU支链相互平行,另外当z=0时,此时动静平台已经相互重合为一个平面了,也是奇异
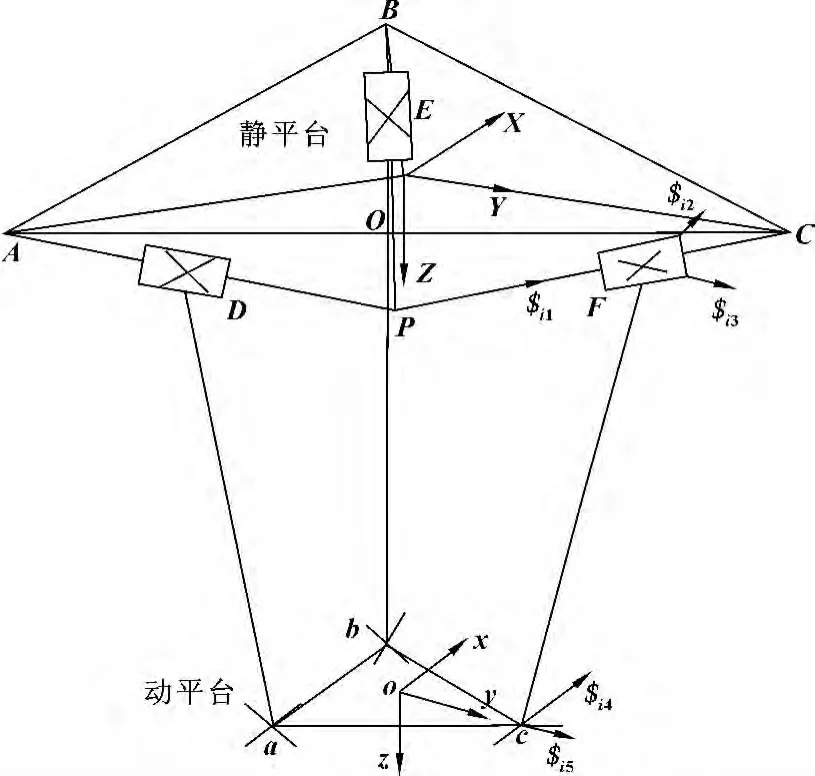
图3 3-PUU并联机构示意图
2.2.1 计算3-PUU并联机构的自由度
运用螺旋理论,求出第i条分支的分支运动螺旋系如下:

同理,利用分支运动螺旋和分支约束螺旋互逆的原理,由分支运动螺旋可以推导出第i条分支的分支约束螺旋系,如下:

由式 (9)可知,其是一个反螺旋力偶矢量,它表示的物理意义是3个分支同时约束了动平台绕着平行于 (0 0 1)的转动,与前面分析的3-UPU并联机构一致,此约束力偶方向与静平台上基座标系的Z轴方向一致,而与静平台相连的万向铰两个轴线分别平行于静平台的X、Y轴,故此约束力偶方向与该万向铰两轴线所在平面垂直,而且静平台处相连的3个万向铰轴线所在平面均不平行也不重合,故3个约束力偶也互不平行,因此,3个约束力偶必会约束动平台的3个转动,此3-UPU并联机构仅拥有3个移动自由度。
2.2.2 作为3-PUU并联机构时的位置逆解的计算


这里已知输出参数x,y,z和机构结构参数R,r,L,l,解3个一元二次方程可以比较容易的求出位置逆解 l1,l2,l3(li≥0,i=1,2,3)。
2.2.3 作为3-PUU并联机构时的位置正解的计算
已知输入参数l1,l2,l3和结构参数R,r,L,l,θ,由式 (10)、(12)可以用MATLAB软件很方便地计算出上面方程组的解x,y,z,且z必取大于零的值,x,y,z的值即为所求的3-PUU并联机构的位置正解。
2.2.4 3-PUU并联机构的雅可比矩阵的求解
同理,将式 (10)、(12)方程组对时间求导可得雅可比矩阵:


2.2.5 3-PUU并联机构奇异位形的分析计算

并联机构均处于奇异位形,此时△abc和△DEF为全等的等边三角形,三支链相互平行,或者当z=0时,此时上下平台会重合一部分,机构也会处于奇异位形。
3 机构的刚度分析
3.1 机构作为3-UPU并联机构时的刚度分析
C GOSSILIN在1990年提出:并联机构在其工作空间内一点的刚度可以通过它的刚度矩阵来描述的,由此他给出了并联机构的刚度矩阵公式:

上述公式 (15)中的Kj为关节刚度矩阵,且为含有常量kii的对角矩阵 (i=1,2,3);J为并联机构的雅可比矩阵,这里取kii=k(i=1,2,3),即3-UPU并联机构的所有支链的刚度值为k,因此,公式 (15)可化简为如下公式:

其中k1,k2,k3依次分别为KC主对角线上的元素,雅可比矩阵J已经求出,对并联机构的结构参数进行赋值,取x=30 mm,y=40 mm,z=100 mm,k=20 N/m,下面根据上述机构参数的值应用MATLAB软件分析3-UPU并联机构的上下平台边长D和d对机构整体刚度K值的影响,如图4、5所示。
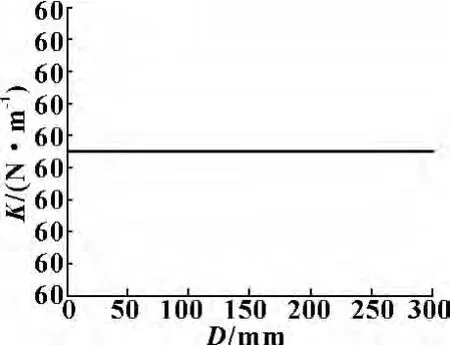
图4 3-UPU并联机构整体刚度K随D值变化曲线图

图5 3-UPU并联机构整体刚 度K随d值变化曲线图
MATLAB绘图结果表明:对于3-UPU并联机构,当末端动平台中心点O相对于静平台的位姿参数确定时 (这里取一组数据值x=30 mm,y=40 mm,z=100 mm,k=20 N/m),3-UPU并联机构的整体刚度值为一个定值60 N/m,即针对3-UPU并联机构而言,其整体刚度值K并不受上下平台机构结构尺寸D和d值的影响,通过改变D和d是无法增大其整体的刚度值的,提升其刚度值还需从其他方面着手。
3.2 机构作为3-PUU并联机构时的刚度分析
同理,对3-PUU并联机构的结构参数进行赋值,取已知输出参数x=30 mm,y=40 mm,z=300 mm,和机构结构参数R,r,L,l,k=20 N/m,下面根据上述机构参数的值,应用MATLAB软件研究3-PUU并联机构的上下三角形平台外接圆半径R和r对机构整体刚度K值的影响。如图6、7、8所示。

图6 3-PUU并联机构整体刚度K随R和r值的变化曲线图

图7 3-PUU并联机构整体刚度K随r值变化曲线图
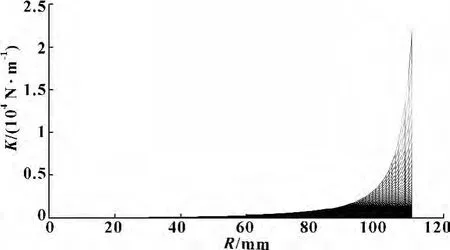
图8 3-PUU并联机构整体刚度K随R值变化曲线图
同理,根据图6—8可以得出:对于3-PUU并联机构,当末端动平台中心点O相对于静平台的位姿参数确定时 (这里取一组数据值k=20 N/m,L=240 mm,x=30 mm,y=40 mm,z=300 mm,l=80 mm),3-UPU并联机构的整体刚度值分别随着R和r的增大逐渐增大,且当R=r=110 mm时,K取得最大值2.161×104N/m,即对3-PUU并联机构而言,可以通过适当的提高其上下平台半径值,来达到增加整体刚度的目标。
4 结论
(1)可实现3-PUU机构和3-UPU机构的组合并联机构在两种机构构型下均能实现3个移动自由度,其整体刚度值与末端位姿参数相关。
(2)当该组合并联机构处于3-UPU机构构型时,机构的整体刚度值不随其上下平台的边长的变化而变化,提升其刚度值还需从其他方面研究;当该组合并联机构处于3-PUU机构构型时,机构的整体刚度值随着上下平台外接圆半径R和r的增大而增大,即可以通过适当的提高上下平台外接圆半径的尺寸来提高此时机构的整体刚度。
(3)当机构中滑块9、10、11和直线驱动器16、17、18均处于未锁死状态时,即机构处于3-PUPU并联机构时,其机构的刚度仍有待于进一步研究。
[1]艾青林,黄伟锋,张洪涛,等.并联机器人刚度与静力学研究现状与进展.力学进展[J].2012,42(5):583 -592.
[2]韩书葵,方跃法,槐创锋.4自由度并联机器人刚度分析[J].机械工程学报,2006,42(增):31 -34.
[3]孟巧玲.并联机构刚度特性分析[D].沈阳:东北大学,2008.
[4]乐林林,李开明.3-(2SPS)并联机构静刚度分析[J].现代设计与先进制造技术,2010,39(13):39-43.
[5]胡波,路懿.求解3-RPS并联机构刚度的新方法[J].机械工程学报,2010,46(1):24 -29.
[6]槐创锋,刘平安,程贤福.基于3UPU-3PUU型组合并联机构的主动振动抑制控制[J].机床与液压,2013,41(9):21-24.
Kinematics and Stiffness Analysis of a Combined Parallel Mechanism
HUAIChuangfeng,CHEN Hua,LIU Pingan,SHU Yingjiang
(School of Mechatronics,East China Jiaotong University,Nanchang Jiangxi330013,China)
By taking a new realized type of combined parallel3-UPU and 3-PUUmechanism as the research object,the degree of freedom and kinematics of the combined mechanismare analyzed in the case of two realize parallelmechanism respectively,to get the forward displacement and inverse displacement analysis in kinematicsofmechanism.According to the Jacobian matrixgotten,stiffness analysis of themechanism was carried out further.Moreover,the stiffnesswas calculated by using the software ofMATLAB,under the given position,to obtain influence graphs of the overall stiffness value through related structural parameters of the up and down platform.It provides the basis of theoretical analysis for the further research of the combined mechanism,and has a certain guiding role in designing it.
Combined parallelmechanism;Kinematics;Jacobian matrix;Stiffness analysis
TP242
A
1001-3881(2015)21-008-5
10.3969/j.issn.1001 -3881.2015.21.002
2014-9-19
国家自然科学基金资助项目 (51265011);江西省自然科学基金资助项目 (Gjj13347)
槐创锋(1981—),男,博士,副教授,主要研究方向为机械设计、机构学、机器人技术。E-mail:hcf811225@163.com。

