空间绳网系统展开动力学特性分析*

刘海涛，张青斌，杨乐平，朱彦伟

(国防科技大学航天科学与工程学院，湖南长沙410073)

近年来，一种绳网捕获、绳系拖曳的离轨服务手段，在航天领域受到日益广泛的关注［1-2］。如图1所示，轨道拖船机动接近目标后，通过一定的发射方式，在空间展开一张由柔性细绳编织的绳网，形成特定构型覆盖包裹目标，并利用连接到绳网上的系绳完成对目标的回收或离轨销毁。作为一种柔性捕获模式，绳网捕获在非合作目标捕获、远距离捕获等方面展现了极大的应用潜力。与传统的机械臂捕获方式相比，绳网捕获具有压缩体积小、发射质量轻、抓捕距离远、容错范围大、对载体影响小等突出优势［2］。

图1 空间绳网捕获示意图Fig.1 Sketch map of space web capture

空间绳网极度柔软，极易出现变形、松弛与缠绕［3］，具有非常复杂的非线性、多柔体动力学特性。由于目前仍然无法准确分析与预测空间绳网的动力学特性，太空与地面的绳网试验过程中经常出现故障。例如，1999年俄罗斯Znamya 2.5反射镜试验出现失败［4］，2006年日本Furoshiki试验中出现了绳索缠绕与松弛现象［5］。国内外学者对空间绳网系统开展了大量研究工作。Mankala等［6］研究了绳系飞网系统的动力学建模与仿真问题，翟光等［7-8］研究了空间绳网系统的捕获偏差与反馈控制问题，他们的研究中都将空间绳网视为质点。陈钦等［9-11］对空间绳网捕获系统进行了系统设计，利用集中质点法建立了空间绳网系统刚柔耦合动力学模型，研究了绳网发射展开过程的动力学问题。于洋等［12-14］分别利用软件THUsolver和ABAQUS建立了飞网抛射展开的有限元模型，研究了飞网在静态和动态环境下的力学特性，比较了两种飞网折叠方式的展开效果。马骏等［15］设计了一种自主机动空间绳网机器人系统，针对该系统采用集中质量法建立了动力学模型。张青斌等［16-17］通过绳网地面试验，校核和改进了空间绳网动力学模型，分析了地面环境和空间环境下绳网展开过程的差异性。本文在此研究基础上进一步开展空间绳网系统动力学分析等方面的研究工作。

1 空间绳网动力学模型

1.1 模型描述

本文研究采用发射质量块的方式展开空间绳网。空间绳网发射机构剖面图如图2所示，柔性绳网压缩封装在网舱内，质量块轴对称式安装并分别连接在绳网的顶点上。当发射机构点火启动后，质量块会以一定的发射速度υ和发射张角α被弹出，牵引绳网逐渐展开并向前飞行。

图2 空间绳网发射机构剖面图Fig.2 Section map of the trigger mechanism of space web

引入地心惯性系OE-XYZ和拖船轨道系O1-xyz，如图3所示。其中拖船轨道系的x轴由地心OE指向拖船质心O1，z轴沿拖船轨道面法向，y轴在轨道面内垂直于x轴并指向运动方向。模型假设为:1)绳索可拉不可压，有纵向的弹性和阻尼;2)忽略绳索结构中的弯曲挠性和接触效应;3)地球视为均质球体，完全中心引力场;4)拖船运行于圆轨道，且不考虑空间绳网发射对拖船轨道的影响;5)不考虑空间绳网在网舱内的折叠位型及其在网舱所受的摩擦力。

空间绳网属于典型的非线性、多柔体系统，目前还很难建立精确的解析模型。为此，采用离散化的建模思路，将空间绳网离散为若干有限段，然后将各绳段的质量集中在两端点，即绳段节点。由于绳索极度柔软，仅能承受拉力，故可假设绳段节点之间节点由“弹簧”相连，而且该“弹簧”只能承受张力，不能承受压力，同时考虑到绳索的阻尼效应，可将各绳段处理为集中质量阻尼弹簧，这就是“半弹簧阻尼(semi-linear springs and dampers)”模型，如图4所示。在后续的动力学建模中，首先计算各绳段的张力，然后计算各绳段所受的外力，并将其等效到绳段两端的节点上，最后联立各节点动力学方程，即可得到绳网系统的动力学方程。

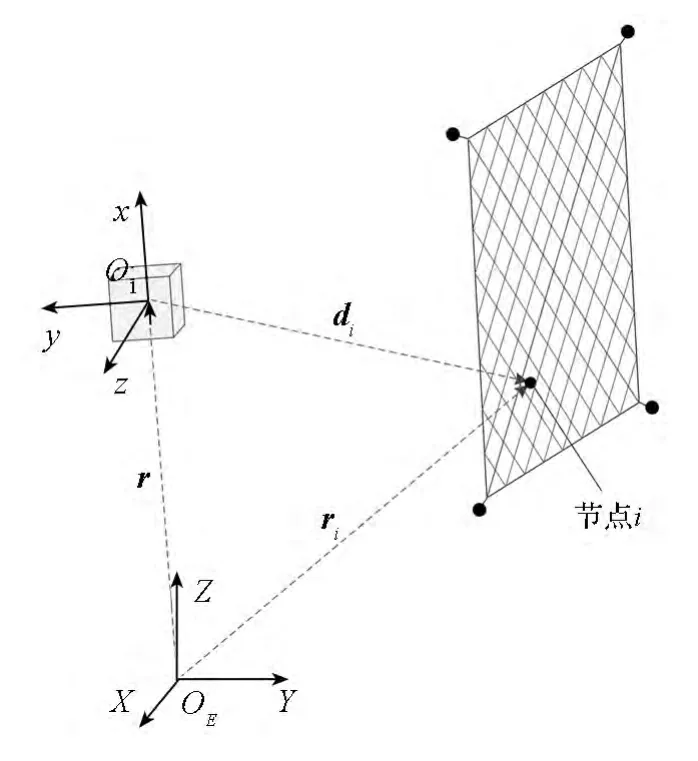
图3 空间绳网的坐标系Fig.3 Coordinate frames of the space web

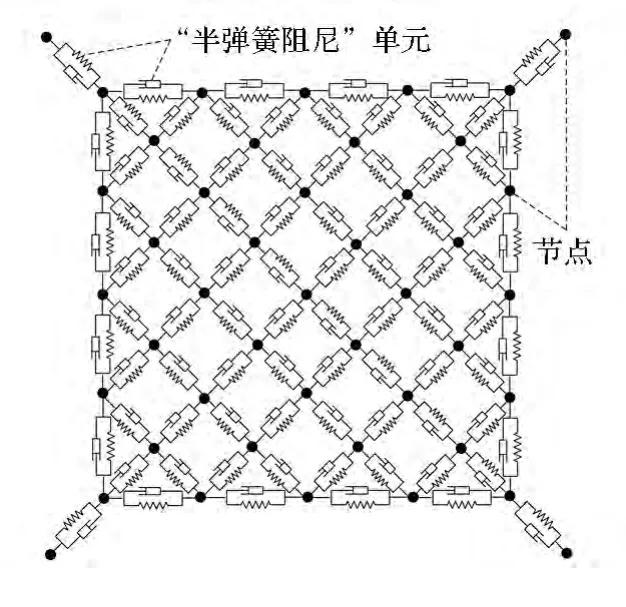
图4 空间绳网的“半弹簧阻尼”模型Fig.4 Semi-linear springs and dampers model of the space web

1.2 绳段单元张力计算

由于绳索极度柔软，仅能承受张力，不能承受压力，同时考虑到绳索的阻尼效应，因此将各绳段单元假设为“半弹簧阻尼”单元。通常，绳段张力可近似为线弹性与线性阻尼之和，如图5所示，绳段sij的张力大小为

式中:lij，iij分别为绳段sij的实际长度及其变化率;kij，cij分别为绳段sij的等效弹性系数与等效阻尼系数，其取值一般通过试验得出。

如图5所示，绳段sij两端的节点为节点i与节点j，在惯性系下的位置矢量分别为r i，r j，则绳段sij的实际长度lij及其变化率iij可如下计算

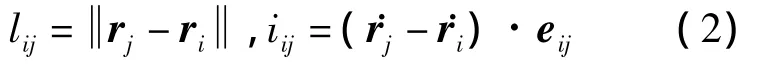
式中e ij为由节点i指向节点j的单位矢量。

图5 绳段sij的张力Fig.5 Tension on the segment sij

1.3 绳段单元外力计算

在空间环境下，绳段受万有引力作用，由于大气稀薄，气动力可忽略不计，而且由于空间绳网展开过程较快，地球非球形摄动等干扰力也可忽略不计。由此作用于绳段sij的外力F exij为

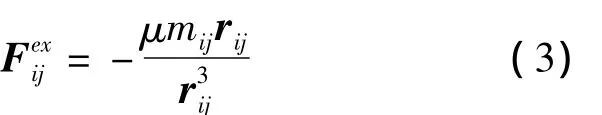
式中r ij为惯性系下绳段sij中心的位置矢量。

在地面环境下，作用于绳段的外力主要包括重力和气动力等，而且气动力可以分解为气动阻力和气动升力，如图6所示，作用于绳段sij的外力为

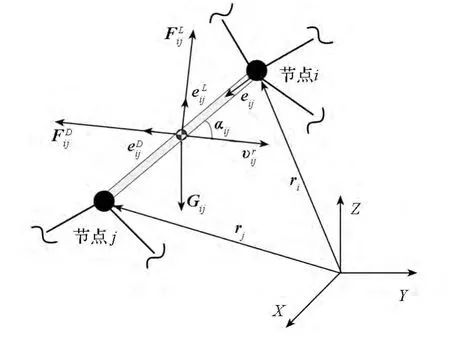
图6 地面环境下作用于sij的外力Fig.6 Outside force on the segment sij on the ground

设地面重力加速度为g，则重力G ij可表示为

式中αij为sij的攻角。

1.4 系统动力学方程

不论是在地面环境，还是在空间环境，节点i的动力学方程都可以在地心惯性系下表示为

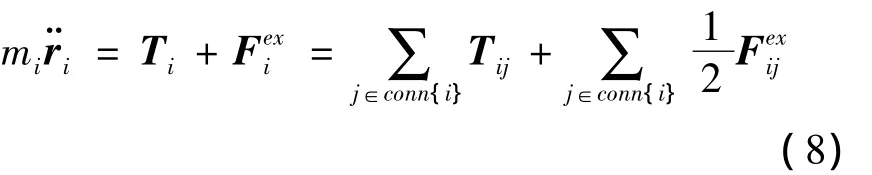
为了便于描述空间环境下的空间绳网展开特性，需要建立空间绳网在拖船轨道系下的相对运动动力学方程。由于拖船运行于圆轨道，由C-W方程，节点i在拖船轨道系下的相对运动方程为

2 空间绳网展开过程仿真分析

2.1 性能参数定义

影响空间绳网展开性能的参数主要有展开面积和飞行距离，下面给出它们的定义。

展开面积可用于描述绳网覆盖范围，它决定了空间绳网可捕获目标的尺寸。由于绳网的柔性，展开过程的形状并不规整。对于正方形绳网，展开面积S可以由空间绳网四个顶点所围成的四边形ABCD的面积来表示，如图7所示，d DA，d CB分别为四边形两条对角线的矢量，则展开面积S可由式(10)近似计算。

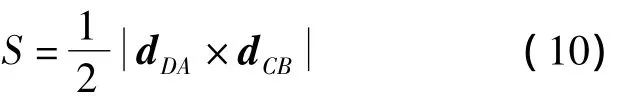
飞行距离是指空间绳网与拖船之间的相对距离，可以表征空间绳网的捕获半径。对于正方形绳网，飞行距离d可以由拖船到空间绳网四个顶点的中心的距离来表示。设拖船到四个顶点的位置矢量分别为d A，d B，d C，d D，则空间绳网四个顶点的中心On的位置矢量为

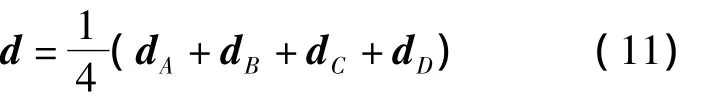
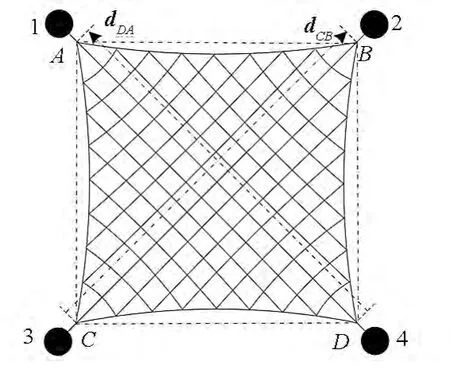
图7 展开面积示意图Fig.7 Sketch map of the deployment area

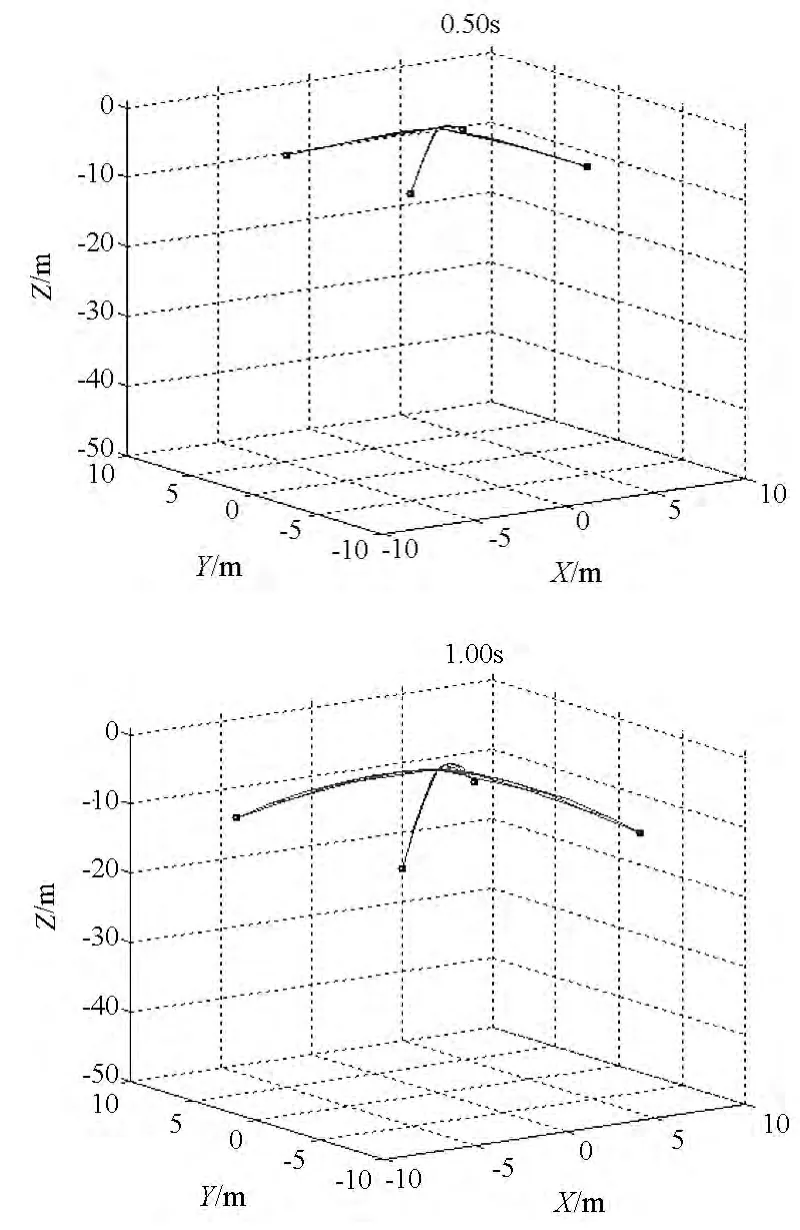
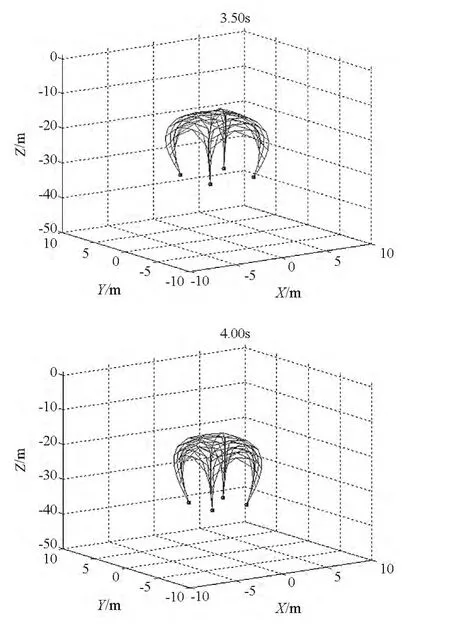
图8 空间绳网地面试验仿真图Fig.8 Simulation diagram of ground test of the space web

2.2 地面试验验证

作者近年来进行了大量的地面试验［10，17］，并通过试验数据校核，改进了空间绳网动力学模型。下面以某次空间绳网地面试验为例，对比试验过程与仿真模型。地面试验采取空中投放的方式，试验中绳网系统从高空竖直向下发射，这样可以有较长时间完成空间绳网展开。仿真参数根据试验参数选取，动力学模型中考虑了空气阻力和重力等外力。

空间绳网地面试验的仿真过程如图8所示，展开面积的试验值与仿真值对比如图9所示，飞行距离的试验值与仿真值对比如图10所示。可以看出，在地面环境下，空间绳网在质量块的牵引下由“+”字形拉出并逐渐展开，在空气阻力和重力作用下，空间绳网呈“降落伞”形状下落。在试验中展开面积的最大值为176.0 m2，在仿真中展开面积最大值为177.2 m2，两者都远远小于空间绳网的设计面积(此处为40 m×40 m)，可见地面环境下空间绳网无法完全展开。在试验与仿真中，展开面积与飞行距离的变化规律基本相似，数值误差也都很小，这充分证明了地面环境下动力学模型的可靠性，也间接说明了空间环境下动力学模型的可靠性。

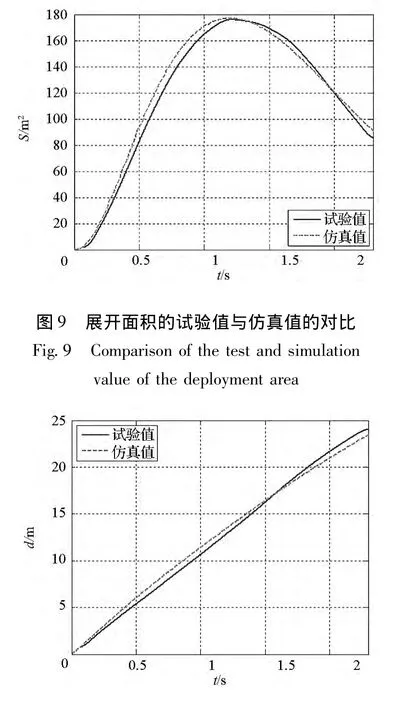
图10 飞行距离的试验值与仿真值的对比Fig.10 Comparison of the test and simulation value of the flying distance

2.3 空间绳网展开动力学特性

下面研究空间环境下的空间绳网展开过程。假设目标位于GEO轨道，拖船位于目标V-bar方向，绳网为边长40 m的正方形绳网。绳网材料为Zylon®纤维，网目尺寸为Lmesh=0.404 1 m，编织绳索的线密度为0.247 5 g/m，由此编织而成的绳网质量为mw=2 kg。此外，单个质量块质量为ms=1.5 kg，发射速度为υ=15 m/s，发射张角为α=30°，绳索阻尼比为ζ=0.5。

空间绳网展开的过程如图11所示，图中柱条表示绳段张力大小，单位为N。从图中可以看出，在质量块的牵引作用下，空间绳网沿对角线呈“+”字形拉出并逐渐展开成面状，展开面积不断变大，此时空间绳网几何构型呈凹形。在一定时刻展开面积达到最大，整个空间绳网几乎在一个平面上。在此之后，由于绳网具有弹性，质量块和网面将发生收缩回弹，展开面积不断变小，而且空间绳网中部的节点将超越质量块向前运动，此时空间绳网几何构型呈凸形。展开面积与飞行距离的变化曲线如图12、图13所示，可以看出展开面积先增大后减小，在图中“〇”处达到最大值，此时飞行时间为5.24 s，展开面积为1580 m2，约为设计面积的98.75%，说明展开效果极佳;飞行距离则随时间不断增加，当展开面积最大时，飞行距离为51.1 m。

图11 空间绳网展开过程图Fig.11 Deploy course of the space web

图12 展开面积变化过程Fig.12 Change process of the deployment area

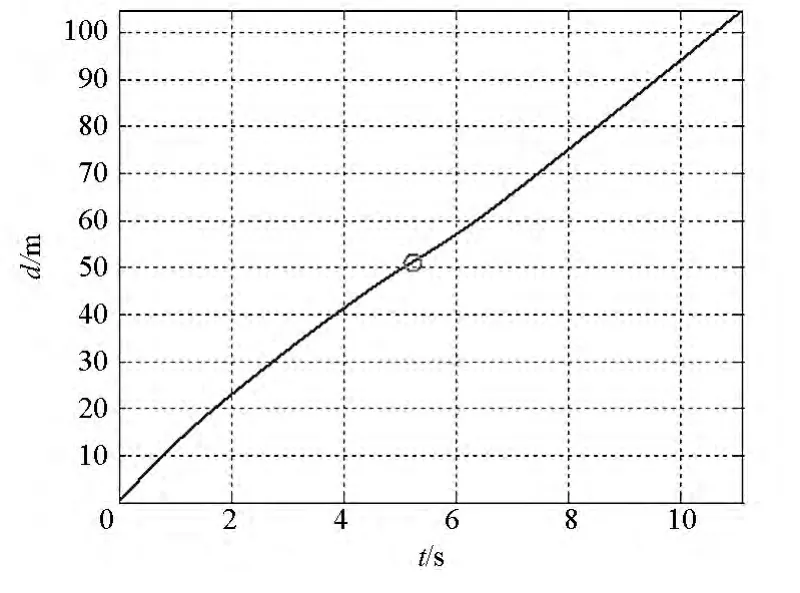
图13 飞行距离变化过程Fig.13 Change process of the flying distance

空间绳网展开过程中的能量变化如图14所示。可以看出，质量块发射后，质量块动能逐渐减小，绳网动能由0逐渐增大，在空间绳网完全展开前后质量块动能达到最小值，绳网动能达到最大值;之后质量块动能又逐渐增大，绳网动能逐渐减小。这一过程说明空间绳网展开过程中，质量块与空间绳网之间发生着复杂的能量传递过程。系统的弹性势能为绳网中所有绳段的弹性势能之和，可以看出整个展开过程中，弹性势能的量级都很小。系统总机械能为系统动能与弹性势能之和，可以看出它始终呈下降趋势，其原因是空间绳网的阻尼效应。

图14 能量变化规律Fig.14 Change rule of the energy

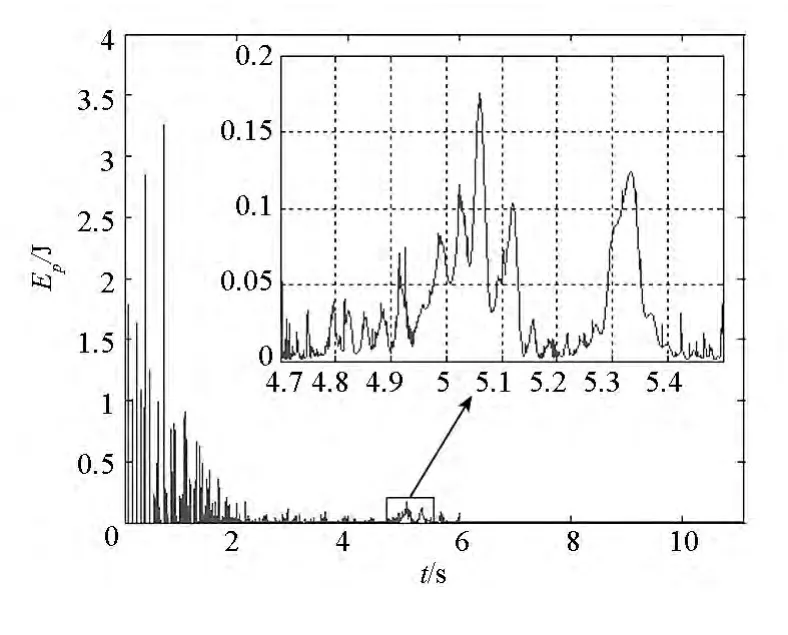
图15 弹性势能变化规律Fig.15 Change rule of the elastic potential energy

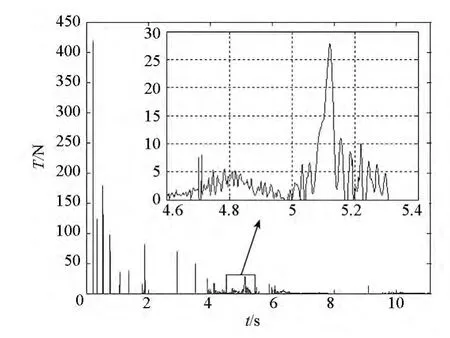
图16 对角线上某绳段单元的张力Fig.16 Tension on the segment at the diagonal

图15为单独表示的弹性势能曲线，图16、图17为两个绳段单元的张力，这两个绳段分别位于对角线和边线，且与图7所示的正方形顶点A相邻。可以看出，起初弹性势能成脉冲式变化规律，这是由于在质量块牵引下，空间绳网中的绳段单元突然被拉紧，然后又迅速回弹，不停地经历张紧与松弛的状态变化，这时绳段单元张力的峰值很大，但作用时间很短;在空间绳网完全展开前后，弹性势能的变化则相对平缓，这是由于此时空间绳网几乎展开成一个平面状(见图11)，在四角的质量块往外的拉力作用下，空间绳网内部的绳段单元有一个持续的张紧过程;在此之后，空间绳网弹性势能更为微弱，这是由于空间绳网中的绳段单元处于长期松弛的状态，而且张紧时张力的峰值也很小。

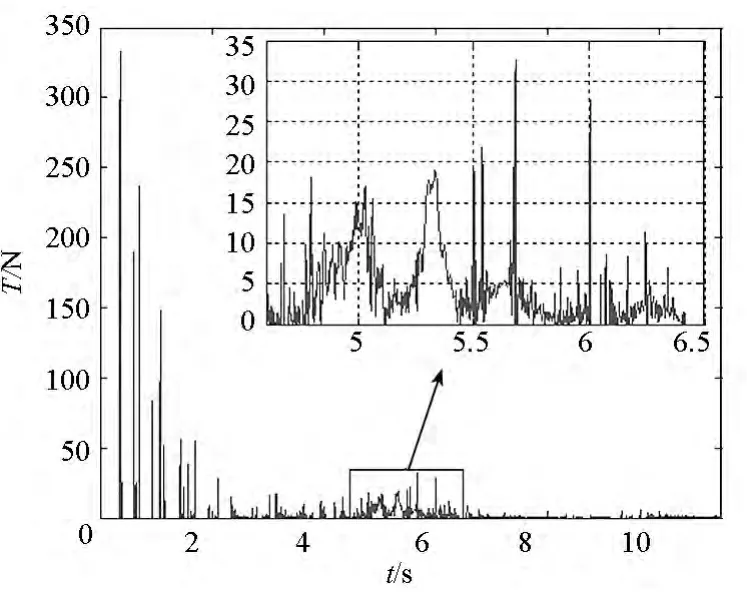
图17 边线上某绳段单元的张力Fig.17 Tension on the segment at the sideline

2.4 轨道高度与捕获方向的影响

空间绳网在不同轨道高度以及不同捕获方向下的展开效果是一个值得关注的问题。如果展开效果不受轨道高度的影响，则可说明空间绳网应用范围的广泛性;如果展开效果不受捕获方向的影响，那么在捕获时只需将发射轴线对准目标并发射绳网即可，不需另行调节其他参数就可以完成捕获。下面分别就空间绳网在GEO、LEO轨道，沿V-bar、R-bar和H-bar这三个典型的捕获方向的展开过程进行仿真研究。仿真中，GEO轨道半径设为42 164 km，LEO轨道半径设为7000 km，其他仿真参数不变。

图18为不同轨道高度与捕获方向的展开面积对比，图19为不同轨道高度与捕获方向的飞行距离对比。可以看出，在各种情况下，空间绳网展开过程的展开面积高度一致，飞行距离也高度一致。这说明轨道高度与捕获方向对展开面积与飞行距离基本没有影响。

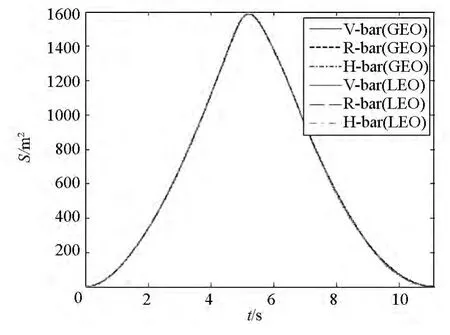
图18 不同轨道高度与捕获方向的展开面积Fig.18 Deployment area of different orbit height and capture direction

尽管轨道高度与捕获方向不影响展开面积与飞行距离，但是由于轨道动力学的作用，不同的轨道高度与捕获方向可能使得空间绳网飞行过程中偏离发射轴线的程度不一样。定义空间绳网在飞行过程中，相对于发射轴线方向的偏移为横向偏移，如果横向偏移过大有可能影响空间绳网成功捕获目标。对于正方形绳网，横向偏移Dax可以由空间绳网四个顶点的中心On到发射轴线的距离来表示，On的位置矢量由式(11)求得，Dax由点到直线的距离公式计算得到。

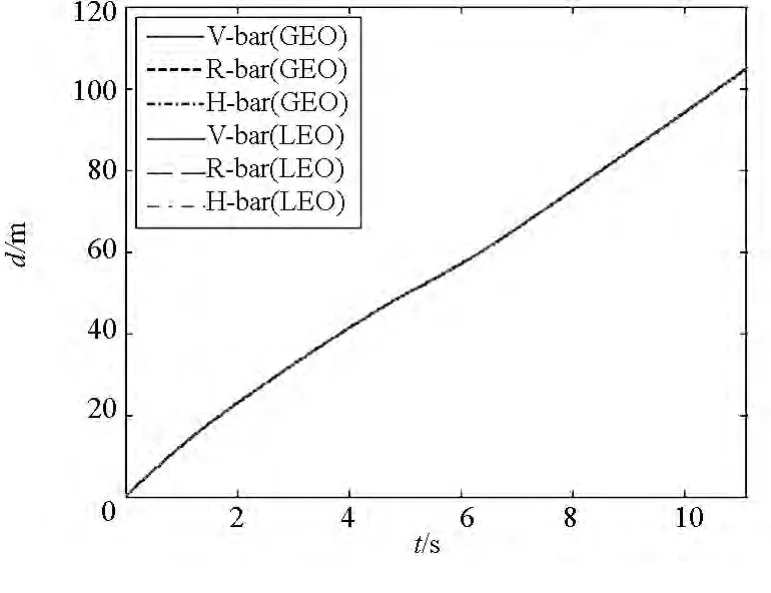
图19 不同轨道高度与捕获方向的飞行距离Fig.19 Flying distance of different orbit height and capture direction

图20、图21分别表示GEO轨道和LEO轨道下，不同捕获方向的横向偏移。可以看出，横向偏移随着时间大致成指数级增长，而且受捕获方向的影响较为明显，捕获方向为V-bar和R-bar时空间绳网的横向偏移比捕获方向为H-bar时的要大。V-bar捕获时，GEO轨道下空间绳网完全展开时(5.24 s)的横向偏移仅为毫米级，而LEO轨道下为分米级。但是，由于空间绳网完全展开后尺寸高达40 m，而且设计时考虑了对目标捕获的冗余度，因此空间绳网捕获完全能够承受这一量级的横向偏移，这体现了绳网捕获的容错性这一优势。

图20 不同捕获方向的横向偏移(GEO)Fig.20 Transverse offset in different capture direction(GEO)

图21 不同捕获方向的横向偏移(LEO)Fig.21 Transverse offset in different capture direction(LEO)

2.5 发射参数的影响

影响绳网展开性能的发射参数有发射速度和发射张角，合理选择发射参数对于捕获任务的实施至关重要。

发射速度分别取10 m/s，15 m/s和20 m/s，发射张角都取30°，其他仿真参数不变，仿真得到展开面积与飞行距离如图22、图23所示，图中“〇”对应着展开面积达到最大的时刻。

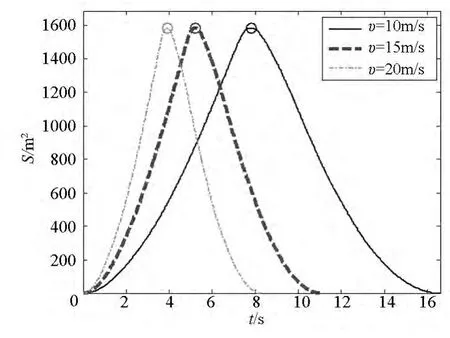
图22 不同发射速度的展开面积Fig.22 Deployment area in different casting velocity

图23 不同发射速度的飞行距离Fig.23 Flying distance in different casting velocity

可以看出，不同的发射速度对展开面积的最大值以及展开面积最大时的飞行距离几乎没有影响;但发射速度越大，达到最大展开面积的时间越短。

发射张角分别取20°，30°和40°，发射速度都取15 m/s，其他仿真参数不变，仿真得到展开面积与飞行距离如图24、图25所示，图中“〇”对应着展开面积达到最大的时刻。可以看出，不同的发射张角对展开面积的最大值几乎没有影响;但发射张角越大，达到最大展开面积的时间越短，而且展开面积最大时的飞行距离越小。

综上可知，不同的发射速度与发射张角对最大展开面积几乎没有影响;但是较大的发射速度与较大的发射张角有利于绳网快速展开，较小的发射张角有利于增大绳网捕获距离。

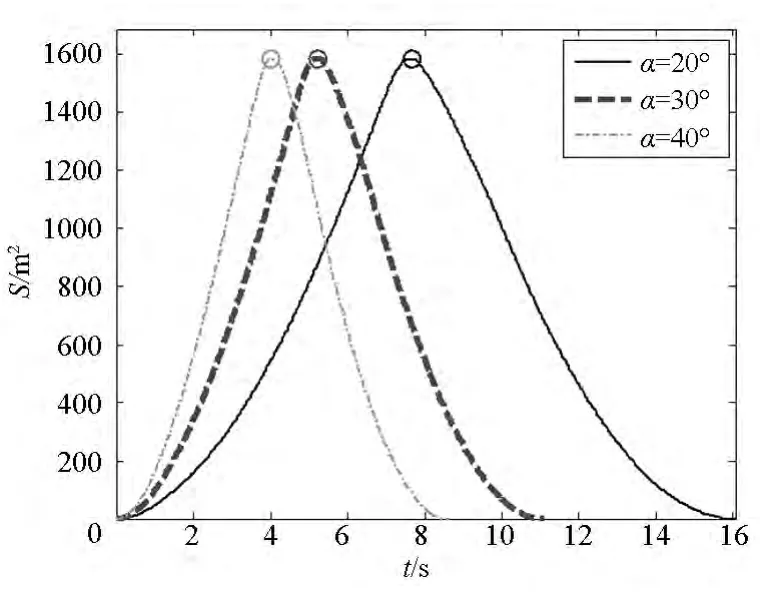
图24 不同发射张角的展开面积Fig.24 Deployment area in different casting angle

图25 不同发射张角的飞行距离Fig.25 Flying distance in different casting angle

3 结论

采用离散化的建模思路，推导了空间绳网动力学模型;通过地面试验验证了动力学仿真模型的有效性;通过仿真，分析了空间绳网展开过程中的动力学特性。

绳网展开过程中，展开面积先逐渐增大，达到最大值后由于弹性发生网面收缩回弹;系统总机械能由于阻尼效应始终呈下降趋势;系统弹性势能的量级很小，而且一直处于剧烈波动状态，这是由于绳网中的绳段单元一直在不断经历张紧与松弛的状态变化。轨道高度和捕获方向不会影响展开面积与飞行距离的变化，但是会产生不同的横向偏移，在LEO轨道能达到分米量级，但由于绳网尺寸的冗余性设计，使得绳网捕获依然有效，体现了绳网捕获容错性的优势。发射速度与张角影响绳网展开性能，较大的发射速度与张角有利于绳网快速展开，较小的发射张角有利于增大绳网捕获距离，可在下一步研究中寻找使展开效果达到最优的发射参数组合。

References)

［1］Bremen A S.Robotic geostationary orbit restorer(ROGER)phase a final report［R］.European Space Agency，2003.

［2］Liu H T，Yang L P，Zhang Q B，et al.An investigation on tether-tugging de-orbit of defunct geostationary satellites［J］.Science China Technological Sciences，2012，55(7):2019-2027.

［3］Tibert G，Gärdsback M.Space webs final report［R］.European Space Agency，2006.

［4］Grossman J.Solar sailing:the next space craze?［J］.Engineering and Science，2000，63(4):18-29.

［5］Nakasuka S，Kaya N.Quick release on experiment results of mesh deployment and phased array antenna by S-310-36［J］.The Forefront of Space Science，2006.

［6］Mankala K K，Agrawal S K.Dynamic modeling and simulation of impact in tether net/gripper systems［J］.Multibody System Dynamics，2004，11(3):235-250.

［7］Zhai G，Qiu Y，Liang B，et al.Research of capture error and error compensate for space net capture robot［C］//Proceedings of the IEEE International Conference on Robotics and Biomimetics，Sanya，China，2007:467-472.

［8］Zhai G，Qiu Y，Liang B，et al.On-orbit capture with flexible tether-net system［J］.Acta Astronautica，2009，65(5-6):613-623.

［9］陈钦，杨乐平.空间绳网系统发射动力学问题研究［J］.宇航学报，2009，30(5):1829-1833.CHEN Qin，YANG Leping.Research on casting dynamics of orbital net systems［J］.Journal of Astronautics，2009，30(5):1829-1833.(in Chinese)

［10］陈钦，杨乐平，张青斌.空间飞网发射动力学建模仿真研究与地面试验［J］.国防科技大学学报，2009，31(3):16-19.CHEN Qin，YANG Leping，ZHANG Qingbin.Dynamic model and simulation of orbital net casting and ground test［J］.Journal of National University of Defense Technology，2009，31(3):16-19.(in Chinese)

［11］陈钦.空间绳网系统设计与动力学研究［D］.长沙:国防科学技术大学，2010.CHEN Qin.Design and dynamics of an orbital net-capture system［D］.Changsha:National University of Defense Technology，2010.(in Chinese)

［12］于洋，宝音贺西，李俊峰.空间飞网抛射展开动力学建模与仿真［J］.宇航学报，2010，31(5):1289-1296.YU Yang，BAOYIN Hexi，LI Junfeng.Modeling and simulation of projecting deployment dynamics of space webs［J］.Journal of Astronautics，2010，31(5):1289-1296.(in Chinese)

［13］李京阳，于洋，宝音贺西，等.空间飞网两种动力学模型的比较研究［J］.力学学报，2011，43(3):542-550.LI Jingyang，YU Yang，BAOYIN Hexi，et al.Simulation and comparison of different dynamical models of space webs［J］.Chinese Journal of Theoretical and Applied Mechanics，2011，43(3):542-550.(in Chinese)

［14］Yu Y，Baoyin H X，Li J F.Dynamic modelling and analysis of space webs［J］.SCIENCE CHINA Physics，Mechanics＆Astronomy，2011，54(4):783-791.

［15］马骏，黄攀峰，孟中杰，等.自主机动空间绳网机器人设计与动力学建模［J］.宇航学报，2013，34(10):1316-1322.MA Jun，HUANG Panfeng，MENG Zhongjie，et al.Design and dynamics modeling of autonomous maneuvering tetherednet space robot system［J］.Journal of Astronautics，2013，34(10):1316-1322.(in Chinese)

［16］Liu H T，Zhang Q，Yang L，et al.Modeling and simulation of deployment dynamics of space webs［C］//Proceedings of the 64th International Astronautical Congress，Beijing，China，2013:2628-2635.

［17］张青斌，孙国鹏，丰志伟，等.柔性绳网动力学建模与天地差异性分析［J］.宇航学报，2014，35(8):871-877.ZHANG Qingbin，SUN Guopeng，FENG Zhiwei，et al.Dynamics modeling and differentia analysis between space and ground for flexible cable net［J］.Journal of Astronautics，2014，35(8):871-877.(in Chinese)

［18］Williams P.Optimal wind power extraction with a tethered kite［C］//Proceedings of the AIAA Guidance，Navigation，and Control Conference，Keystone，Colorado，2006.

［19］Williams P，Sgarioto D，Trivailo P.Optimal control of an aircraft-towed flexible cable system［J］.Journal of Guidance，Control and Dynamics，2006，29(2):401-410.