双弹性垫板刚度对扣件减振性能影响研究

兰海洋,金　浩,刘维宁,孙晓静

(1.绍兴文理学院土木工程学院, 浙江绍兴　312000； 2.北京交通大学土木工程学院, 北京　100044)



双弹性垫板刚度对扣件减振性能影响研究

兰海洋1,金浩1,刘维宁2,孙晓静2

(1.绍兴文理学院土木工程学院, 浙江绍兴312000； 2.北京交通大学土木工程学院, 北京100044)

摘要：为了研究垫板刚度对地铁中大量使用的双弹性垫板扣件减振性能的影响,通过对简化模型的理论推导,以及采用实验室测试和数值模拟相结合的方法,得出：板下垫板刚度越大,则轨道板位移频响越大,轨下垫板刚度大小对轨道板振动位移频响基本没有影响；轨下垫板刚度以及板下垫板刚度越大,则轨道板振动加速度频响越小。因此,设计开发双弹性垫板的扣件,应该根据轨道板位移控制和加速度控制综合考虑。

关键词：地铁；轨道扣件；双弹性垫板；刚度；振动

随着城市轨道交通的大量投入使用，由此引发的振动问题也日益受到关注[1-5]。相较于梯式轨道[6-9]和浮置板轨道[10-11]等轨道减振措施，弹性扣件的减振能力较小[12]。

目前，在地铁中广泛使用的具有双弹性垫板(轨下垫板和板下垫板)的DTVI2扣件，相比于单一弹性垫板扣件，具有中间质量块(铁垫板)这一鲜明特性。如何选择轨下垫板刚度和板下垫板刚度，直接影响列车运行的安全性和平稳性。

本文通过理论推导、实验室测试和数值模拟相结合的方法，研究了轨下垫板刚度和板下垫板刚度对扣件减振性能的影响。

1数学模型

钢轨、扣件(略去弹条等)和轨道板横截面如图1所示。

图1　钢轨、扣件和轨道板横截面

基本假定：

(1)m1为钢轨和轨下垫板质量的和，c1为轨下垫板阻尼，k1为轨下垫板刚度，不考虑钢轨刚度和阻尼，x1为钢轨和轨下垫板子系统的位移；

(2)m2为铁垫板和板下垫板质量的和，c2为板下垫板阻尼，k2为板下垫板刚度，不考虑铁垫板刚度和阻尼，x2为铁垫板和板下垫板子系统的位移；

(3)m3、c3、k3以及x3分别为轨道板质量、阻尼、刚度和位移；

(4)f1为激振力，令f1=f(t)。

该系统简化模型如图2所示。

图2　简化模型

根据简化模型，利用d’Alembert原理可以得到

(1)

(2)

(3)

存在:F(ω)=F[f(t)]，X1(ω)=F[x1(t)]，X2(ω)=F[x2(t)]，X3(ω)=F[x3(t)]

根据式(1)、式(2)和式(3)，令K1=m1ω2，K2=m2ω2，K3=m3ω2，则在不考虑阻尼的情况下可以得到位移频响函数

根据Fourier变换的微分性质，进一步可以得到加速度频响函数

Hd(ω)和Ha(ω)可以改成如下形式

式中

B1=-k1k3

k1m1m3+k1m2m3)]

假如轨道板和隧道刚性连接，即k3相较于k1和k2无穷大，则可以得出如下结论。

①对于位移频响函数

因此，对于轨道板位移控制，应该降低板下垫板刚度同时增大钢轨质量和铁垫板质量，从而缩小位移随频率单调增大的范围；轨下垫板刚度的大小不影响位移随频率单调增加的范围。

②对于加速度频响函数

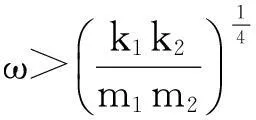
因此，对于轨道板加速度控制，应该增大轨下垫板刚度和板下垫板刚度，同时减小钢轨质量和铁垫板质量，从而可以增大加速度随频率单调递减的范围。

2激振力获取和Abaqus建模

2.1激振力获取

在北京交通大学轨道减振与控制实验室进行了落锤激励试验，实验室位于地下18m深处，可以很好地模拟地铁环境。轨道试验台安装DTVI2扣件以及60kg/m钢轨，动态响应测试位置如图3所示。

图3　测试位置

测试用垫板材料参数如表1所示。控制落锤激振力最大幅值为40 kN，采样频率12.8 kHz；测试轨道板振动加速度，采样频率1.6 kHz。利用变时基传递函数细化分析方法， 解决力信号时域波形精度与加速度信号频率分辨率之间的矛盾， 提高低频脉冲频响分析精度[2]。

表1　垫板材料参数

测试得到激振力时程，如图4所示。

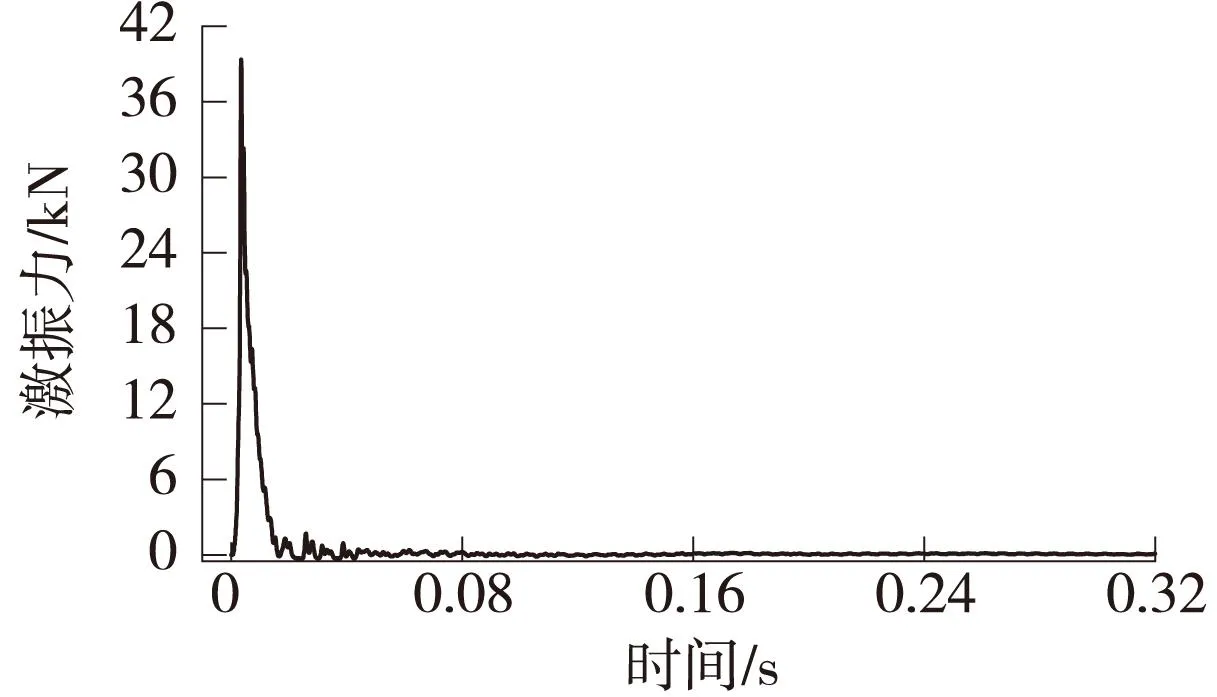
图4　激振力时程曲线

2.2Abaqus建模

选用Abaqus有限元软件进行数值模拟。钢轨简化为刚体，轨下垫板和板下垫板简化为弹簧。

垫板材料参数用测试的材料参数，见表1；混凝土密度2 500 kg/m3，弹性模量125×1010Pa，泊松比0.2；铁垫板密度7 850 kg/m3，弹性模量34×1011Pa，泊松比0.3。

激励荷载采用图4测试得到的激振力。

3数值分析

考虑轨下垫板和板下垫板不同的刚度，分别取值。取值范围10～90 MN/m，每隔10 MN/m取1个值。

每组刚度都可以得到相应的位移频响函数和加速度频响函数。根据理论推导的位移频响和加速度频响的变化规律，采用位移频响最大值和加速度频响最小值作为研究对象，并且用B-spline曲线进行拟合。

轨下垫板刚度为10 MN/m时，轨道板位移频响最大值和加速度频响最小值随板下垫板刚度变化情况，如图5和图6所示。

图5　轨道板位移频响最大值与板下垫板刚度关系曲线

图6　轨道板加速度频响最小值与板下垫板刚度关系曲线

由图5和图6可以得出：轨下垫板刚度一定时，随着板下垫板刚度的增加，轨道板位移频响最大值整体上呈现增大的趋势；加速度频响最小值整体上呈现减小的趋势。

板下垫板刚度为10 MN/m时，位移频响最大值和加速度频响最小值随轨下垫板刚度变化情况，如图7、图8所示。

图7　轨道板位移频响最大值与轨下垫板刚度关系曲线

从图7和图8可以得出：板下垫板刚度一定时，随着轨下垫板刚度的增加，轨道板位移频响最大值整体上没有增大或者减小的趋势；加速度频响最小值整体呈现减小趋势。

比较图5与图7，板下垫板刚度增大能明显的增大轨道板位移频响最大值，轨下垫板刚度基本不发挥作用。比较图6和图8，轨下垫板刚度和板下垫板刚度增大，都会使轨道板加速度频响最小值减小。数值模拟得到的结果和理论推导结果相吻合。

图8　轨道板加速度频响最小值与轨下垫板刚度关系曲线

4结论

通过对简化模型的理论推导，以及采用实验室测试和数值模拟相结合的方法，得出如下结论。

板下垫板刚度越大，则轨道板位移频响越大，轨下垫板刚度的大小对轨道板位移频率的响应基本无影响；轨下垫板刚度和板下垫板刚度越大，则轨道板振动加速度频响越小。

因此，设计开发双弹性垫板的扣件，应该根据轨道板位移控制和加速度控制综合考虑。

参考文献：

[1]Xia H, Zhang N, Cao Y M. Experimental Study of Train-Induced Vibrations of Environments and Buildings[J]. Journal of Sound and Vibration， 2005(3):1017-1029.

[2]王文斌，刘维宁.更换减振扣件前后地铁运营引起地面振动的研究[J].中国铁道科学,2010,31(1):87-92.

[3]马蒙，刘维宁，丁德云，等.地铁列车振动对精密仪器影响的预测研究[J].振动与冲击,2011(3):185-190.

[4]贾颖绚，郭猛，刘维宁，等.列车振动荷载对古建筑的动力影响[J]. 北京交通大学学报,2009(1):118-122.

[5]李克飞，韩志伟，刘维宁，等.基于现场锤击试验的地铁轨道振动特性分析及参数研究[J].铁道标准设计,2014(2):12-16.

[6]金浩，刘维宁.蚁群算法耦合LS-DYNA梯式轨枕轨道动力特性优化[J].振动与冲击,2013(2):24-28.

[7]金浩，刘维宁，王文斌.梯式轨枕轨道模态试验分析[J].工程力学,2013(3):459-463.

[8]王文斌，刘维宁，马蒙，等.梯形轨道系统动力特性及减振效果试验研究[J].中国铁道科学,2010,31(2):24-28.

[9]陈伯靖，周建，李成辉.浮置式梯形轨枕轨道减振器刚度对轨道动力特性影响分析[J].铁道标准设计,2013(1):5-7.

[10]丁德云，刘维宁，李克飞，等.钢弹簧浮置板轨道参数研究[J].中国铁道科学,2011,32(1):30-35.

[11]刘维宁，丁德云，李克飞，等.钢弹簧浮置板轨道低频特征试验研究[J].土木工程学报,2011,44(8):118-125.

[12]孙家麒.城市轨道交通振动和噪声控制简明手册[M].北京: 中国科学技术出版社,2002.

Research on Vibration Reduction Performance of Fasteners Affected by Stiffness of Double Elastic PadsLan Hai-yang1, Jin Hao1, Liu Wei-ning2, Sun Xiao-jing2

(1.College of Civil Engineering, Shaoxing University, Shaoxing 312000, China;

2.School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)

Abstract：In order to understand the impact of the stiffness of the pad on the vibration reduction performance of fasteners with two elastic pads, this paper, by means of theoretical derivation of simplified model, laboratory test and numerical simulation, concludes that with the increase of the stiffness of the pad under slab, the frequency response of slab displacement increases. The pad stiffness under rail hardly affects frequency response of track slab displacement. The bigger the stiffness of the pad under rail the pad under slab, the smaller the frequency response of track acceleration. Therefore, fasteners with double elastic pads should be designed and developed based on displacement and acceleration of track slab vibration.

Key words：Metro; Track fastener; Double elastic Pad; Stiffness; Vibration

中图分类号：U231

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2015.02.003

文章编号：1004-2954(2015)02-0009-04

通讯作者：金浩(1986—)，男，讲师，博士，E-mail：zhujijinhao@gmail.com。

基金项目：国家自然科学基金项目(51008017)；高等学校博士学科点专项科研基金(20110009120023)

收稿日期：2014-05-10； 修回日期：2014-05-27