长大坡道铺设无缝道岔可行性分析
张梦楠,颜 乐,王 平,王 健
(西南交通大学高速铁路线路工程教育部重点实验室, 成都 610031)
长大坡道铺设无缝道岔可行性分析
张梦楠,颜乐,王平,王健
(西南交通大学高速铁路线路工程教育部重点实验室, 成都610031)
摘要:基于有限单元法建立无缝道岔非线性阻力计算模型,分析不同工况条件下的钢轨纵向力及位移。计算结果表明:坡度对无缝道岔的受力及变形是不利的;随着阻力减小区段距道岔距离增加,钢轨纵向力、最大位移增加,尖轨相对基本轨的位移减小。道床捣固不密实引起的道床纵向阻力减小,会显著增大道岔各部分受力和变形。建议:(1)在大坡道地段,宜采用全长淬火钢轨或高强度钢轨;(2)在进站道岔前列车频繁制动地段、无缝道岔尖端、辙跟、叉心处宜布置观测桩,随时观测无缝道岔的爬行情况;(3)加强无缝道岔防爬锁定;(4)加大上坡方向道床的堆积厚度,并加强捣固。
关键词:长大坡道;无缝道岔;有限单元法;非线性阻力
随着我国高速铁路建设的深入,无缝道岔作为跨区间无缝线路的关键技术[1],近年来得到了迅猛发展。但是由于环保、节约用地或者地形条件的限制,部分道岔不得不设置在坡度超过6‰的大坡道上[2]。道岔铺设在大坡道上将恶化道岔运营环境,容易引起线路爬行,不利于行车的安全性和舒适性。目前,国内外尚无大坡道地段道岔铺设、维护及运营管理的经验,列车通过道岔舒适性和安全性能否得到保证,道岔结构是否安全和耐久,都有待进一步的科学论证。
1计算原理及模型
1.1计算原理
如图1所示,当道岔直股侧股均与区间线路焊连时,右边将承受4根钢轨所传递的固定区温度力Pt,而左边只承受2根钢轨所传递的固定区温度力Pt;当无缝道岔仅直股与区间线路焊连时,右边将有2根钢轨承受Pt,2根钢轨承受接头阻力PH。这样无缝道岔左右端承受的温度力是不平衡的,将引起无缝道岔中钢轨与岔枕向左端位移[3]。

图1 无缝道岔受力示意
岔枕在无缝道岔温度力的传递中起着重要作用[4]。道岔里轨(直曲基本轨为外轨,其余钢轨均为里轨)类似于无缝线路的伸缩区,引起岔枕的纵向位移及偏转、弯曲,进而引起道岔外轨的位移,产生伸缩附加力。无缝道岔直侧股钢轨间通过限位器、间隔铁等传力部件[5],将道岔里轨的温度力向外轨传递。这些传力部件的阻力位移特性曲线是影响外轨附加温度力和里轨伸缩位移的重要部件,需控制在合适的范围内。
1.2计算模型
基于有限单元法所建立的无缝道岔非线性阻力计算理论,是在吸取各种计算理论的优点,克服其缺点的基础上而发展的,该计算模型采用有限元分析法,以一根轨枕的钢轨扣件节点为一个单元,建立节点作用力平衡方程[6-7],对道床纵向阻力、扣件纵向阻力、岔枕变形以及尖轨的限位器、心轨处的间隔铁阻力等因素的作用可进行全面、真实、合理的考虑,比较符合实际情况。该计算模型的另一特点是能更方便地对道岔中的每一作用力因素变化和道岔结构每一部分的作用影响作具体分析,进行方案比较,可对加强、改善道岔结构起理论指导作用。
模型作如下简化:将钢轨简化成与60 kg/m轨截面相同的梁;将轨枕简化为梯形截面梁;扣件、限位器、间隔铁均采用非线性弹簧单元模拟[8]。只考虑道岔的纵向运动。为了尽可能减小边界条件的影响,模型长度选取200 m。模型中,扣件和钢轨、扣件和轨枕通过节点位移耦合相连,限位器、间隔铁通过节点与钢轨位移耦合相连;轨枕与地基通过均布弹簧相连[9];钢轨端部用非线性弹簧固定。
1.3计算参数
以60 kg/m钢轨18号可动心轨无缝道岔为例进行计算分析,该道岔的结构特点为:混凝土岔枕;弹条Ⅲ型扣件,尖轨跟端设2组限位器,限位器子母块间隙7 mm,长心轨跟端与长翼轨间由4个间隔铁联结,短心轨为斜接头,跟端与翼轨间由3个间隔铁联结。直侧股钢轨均焊接。铺设时道岔与区间线路锁定轨温一致。
道岔导曲线半径为1 100 m。道岔区内直股岔枕为133根,尖轨尖端位于第4号岔枕上,尖轨跟端导曲线在第35号岔枕上开始有扣件联结,限位器位于第35、36号与37、38号岔枕间,心轨尖端位于92号岔枕上,长翼轨末端位于113号岔枕上,心轨跟端在109号岔枕上开始有扣件联结,最后一根长岔枕编号为122号。
2力学分析
2.1等效轮轨黏着系数
制动力通过轮轨摩擦直接作用于轨面。制动黏着系数是指制动时轮轨接触点处的最大静摩擦系数,它可用式Fmax=Qμ表示,μ为轮轨黏着系数,Fmax为制动时轮轨间产生的最大制动力,Q为轮轨间的垂直力。我国多年的试验研究和工程实践证明,轮轨黏着系数采用0.164是合适的[10]。
当道岔位于坡道上时,制动荷载还应叠加上活载的坡道分力。在计算中通过将坡道上的制动荷载转化为等效轮轨黏着系数μ0实现。在图2中,设计荷载为Q,平行于轨道的分力F2即为坡道分力[11]。
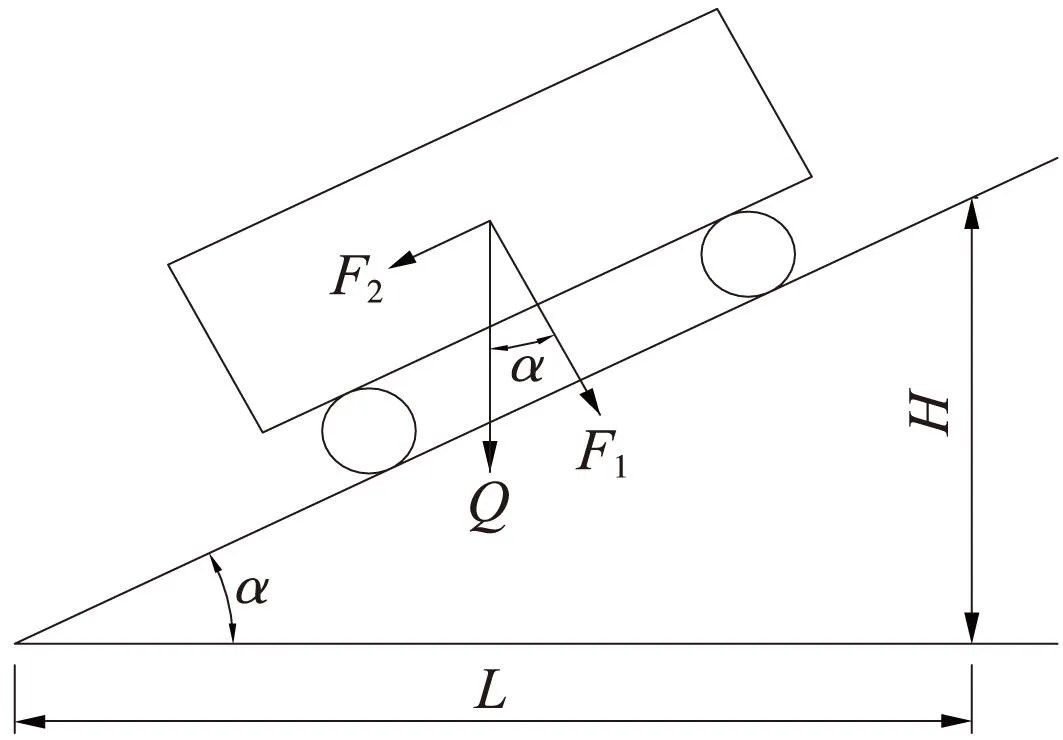
图2 坡道分力示意
根据图2所示几何关系,得F2=Q×sinα。
由于α角一般很小,可令sinα≈tanα,于是F2=Q×tanα。线路坡度i=H/L=tanα,故F2=Q×i。
因此,长大坡道上的等效轮轨黏着系数为μ0=μ+i即μ0=0.164+i,作用于轨面的制动力集度q=μ0×Q[12]。
2.2坡道坡度的影响规律分析
为了研究长大坡道上无缝道岔的力学特性随坡度的变化,选取6种不同的坡度,分别包括平坡,即0‰,以及4‰、8‰、12‰、16‰、20‰。
2.2.1温度荷载作用
在温度荷载作用下,钢轨纵向力及位移如表1所示。
由表1可知,在温度荷载作用下,坡道的坡度对无缝道岔各部件的受力及位移几乎无影响。
2.2.2制动荷载作用
在制动荷载作用下,钢轨纵向力及位移如表2所示。

表1 温度荷载作用下钢轨纵向力、位移对比
由表2及图3可知,在制动荷载作用下,坡道的坡度对无缝道岔的受力和位移有明显影响。随着坡度的增大,钢轨纵向力、位移、间隔铁纵向力、心轨相对翼轨的位移及尖轨相对基本轨的位移都相对成比例增大。坡度每增大10‰,钢轨纵向力增大7.8%,钢轨位移增加6%,间隔铁受力增加6%,心轨相对翼轨的位移增加6%,尖轨相对基本轨的位移增加8.3%。

表2 制动荷载作用下钢轨纵向力、位移对比
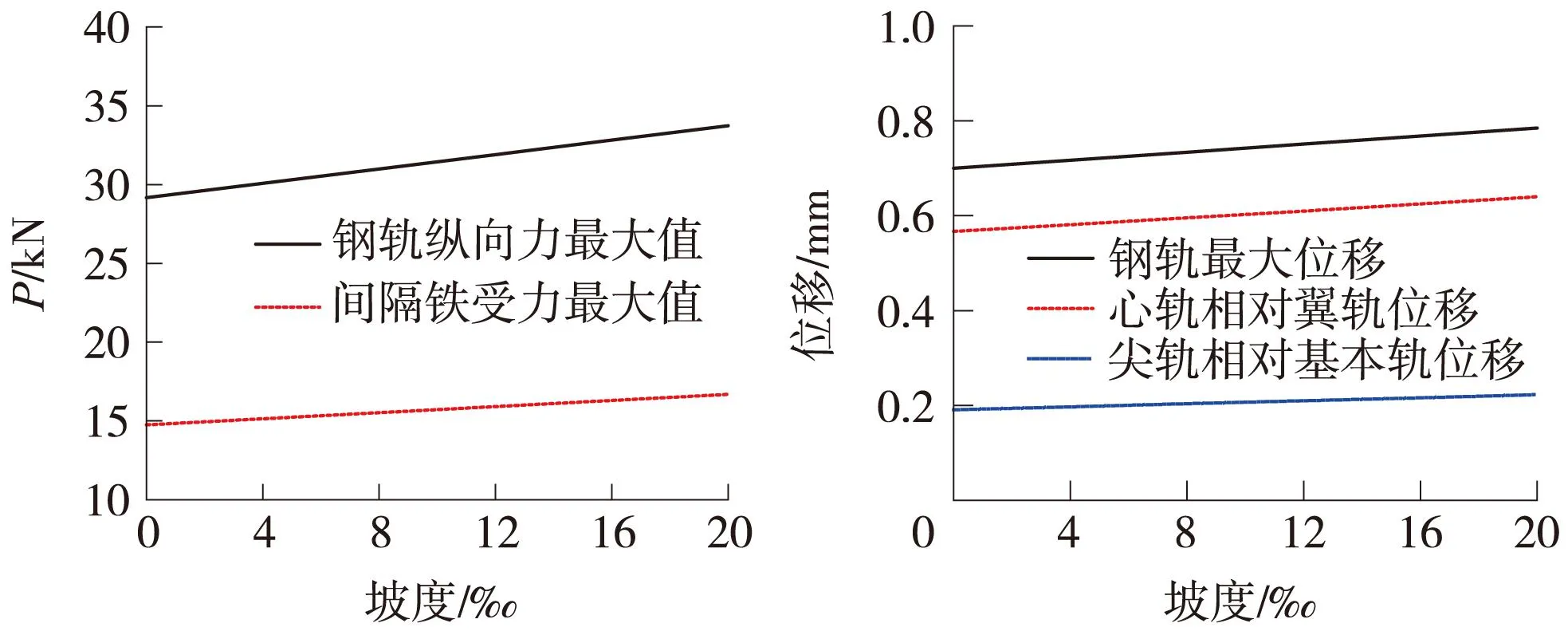
图3 不同坡度对钢轨纵向力、位移影响
2.3制动力方向的影响规律
为了研究制动力的方向对长大坡道道岔受力的影响,考虑2种制动力方向,工况1:制动力方向从坡底指向坡顶;工况2:制动力方向从坡顶指向坡底。坡度取20‰。无缝道岔的钢轨纵向力及位移如表3所示。

表3 钢轨纵向力、位移对比
由表3可知,2种工况的钢轨温度力和位移分布明显不同,工况2的钢轨纵向力比工况1的增加了9.2%,钢轨最大位移增加了1.2%,总体上看,制动力方向从坡顶指向坡底时对无缝道岔的力学特性的影响较为不利。
2.4荷载及荷载组合的影响
为了研究荷载及荷载组合对长大坡道无缝道岔力学特性的影响规律,考虑2种工况,工况1:单独作用温度荷载,钢轨温度变化幅度为50 ℃;工况2:温度荷载+最不利制动荷载组合。制动力方向从坡顶指向坡底,坡度为20‰,无缝道岔的钢轨纵向力及位移如表4所示。

表4 钢轨纵向力、位移对比
由表4可知,工况2比工况1的钢轨纵向力增加了8.2%,钢轨最大位移增幅为30%,间隔铁受力及心轨相对翼轨位移的变化不明显,分别减小了1.5%和2.6%,尖轨相对基本轨位移增幅为10.3%。可见,温度荷载+最不利制动荷载组合的作用对长大坡道上无缝道岔的受力较为不利,建议设计时进行此种荷载组合的受力及变形检算。
2.5阻力减小区段距道岔的距离
由于大坡道上的道床阻力分布不均匀,特此分析道床阻力减小区段距道岔的距离对无缝道岔的影响。
分别取距离岔前20,30,40,50,60 m,使其阻力减小50%,分析其制动工况时对无缝道岔的影响。
通过图4和表5可以看出,随着阻力减小区段距离增加,钢轨纵向力、最大位移增加,尖轨相对基本轨的位移减小但变化不明显,心轨相对翼轨位移基本无变化。因此,阻力减小区段距离道岔越远,对道岔受力变形越不利。其中,钢轨纵向力最大值在道床阻力减小区段距离为60 m时比距离为20 m时增加了11%,钢轨最大位移在道床阻力减小区段距离为60 m时比距离为20 m时增加了44%。

图4 道床阻力减小区段距离对钢轨纵向力、钢轨位移的影响

距离/m钢轨纵向力最大值/kN钢轨最大位移/mm间隔铁受力最大值/kN心轨相对翼轨位移/mm尖轨相对基本轨位移/mm2040.080.5840.4650.031.6733042.530.6980.4680.031.6564043.670.7790.4700.031.6495044.240.8400.4710.031.6466044.510.8820.4710.031.644
2.6阻力减小率的影响
减小道岔区的道床阻力,分别减小10%、25%,以及增加10%、25%,分析其变化对无缝道岔受力的影响。
根据表6和图5,可以得到:道床捣固不密实引起的道床纵向阻力减小,会显著增大道岔各部分受力和变形。道床阻力增加相比无变化时,钢轨最大纵向力、最大纵向位移、间隔铁受力都减小,而尖轨相对基本轨位移增加;道床阻力增加幅度越大,钢轨最大纵向力及间隔铁受力也随之增加,钢轨最大纵向位移和尖轨相对基本轨位移则随之减小。反之,道床阻力减小相比无变化时,钢轨最大纵向力、最大纵向位移、间隔铁受力都增加,而尖轨相对基本轨位移减小;道床阻力减小幅度越大,钢轨最大纵向力、钢轨最大纵向位移及间隔铁受力随之减小,尖轨相对基本轨位移则随之增大。
表6 道床阻力减小率对无缝道岔的影响

图5 道床阻力减小率对钢轨纵向力、钢轨位移的影响
3可行性分析
3.1强度
从受力变形的角度出发,随着坡度的增大,钢轨纵向力、位移、间隔铁纵向力、心轨相对翼轨的位移及尖轨相对基本轨的位移都相对成比例增大,但是都未超过允许的受力变形范围,因此其强度满足规范要求。
3.2稳定性
由于移动轮载施加于钢轨上的纵向力,坡道分力以及制动力等原因,导致长轨条产生不均匀的拉伸和压缩,即产生爬行现象。现场的实际现象反映,在大坡道上,爬行现象很常见[13]。虽然有的线路在现场通过设置防爬设备,采用弹性扣件,加强道床捣固等措施来减缓线路爬行,但是仍有很多线路仅仅通过“爬过去,拉回来”的方法,爬行现象的频率越来越高,都未从根本上解决线路的爬行问题。
因此,大坡道上的线路爬行是个亟需解决的核心问题。
3.3其他因素
长大坡道上经常需要制动,制动还需要考虑的一个重要因素就是机车的紧急制动距离。紧急制动距离是检验列车制动能力和运行安全性的重要技术条件,同时也是通信信号系统设计和运输组织合理规划的重要依据。目前,已有专家学者研究出各种对应不同坡度的动车组的限制速度,我们也可以根据机车的速度和紧急制动距离计算出其限制坡度。但普通电气化机车还缺乏研究。同时,还需要综合考虑桥上无缝道岔的梁轨相互作用,以及在桥梁区段的线路爬行问题等各种因素。
4结论及建议
原则上,在大坡道铺设无缝道岔,其各个方面的受力变形均未超出规范要求,但是需要考虑其在时间累积作用下的爬行问题,以及机车车辆的限制因素等。且如今还未有很好的理论来解释和解决线路的爬行现象,因此其可行性仍需深入研究。
根据现场的运营实践经验,提出以下建议。
(1)在大坡道地段,宜采用全长淬火钢轨或高强度钢轨。
(2)在进站道岔前列车频繁制动地段、无缝道岔尖端、辙跟、叉心处宜布置观测桩,随时观测无缝道岔的爬行情况。观测桩宜布置在道岔前后25 m处,间距大于45 m,且在限位器、长心轨跟端等部位应单独布设观测桩。
(3)应加强无缝道岔防爬锁定,建议在大坡道上安装防爬器或者防爬撑来防止线路爬行,并加密防爬观测次数,发现问题后应及时整治。
(4)在重力作用下,道砟会向下坡道方向堆积,使得上坡方向的道砟不够密实,线路阻力减小,因此建议加大上坡方向道床的堆积厚度,并加强捣固,确保道砟密实、砟盒饱满。
参考文献:
[1]高亮,刘衍峰,田新宇.铁路跨区间无缝线路关键技术的试验研究[J].土木工程学报,2005,38(11):128-131.
[2]易思蓉.铁道工程[M].北京:中国铁道出版社,2009:408.
[3]王平,刘学毅.无缝道岔计算理论与设计方法[M].成都:西南交通大学出版社,2007:101-102.
[4]王树国.大号码无缝道岔纵向力和位移的有限元计算[D].北京:铁道科学研究院,2005.
[5]王平,刘学毅.无缝道岔受力与变形的影响因素分析[J].中国铁道科学,2003,24(2):58-66.
[6]马战国.固定式道岔钢轨纵向力及位移分析[J].铁道建筑,1998(9):11-14.
[7]马战国.道岔侧线对无缝道岔的影响[J].中国铁道科学,1994,18(4):57-62.
[8]杨荣山.桥上无缝道岔纵向力计算理论与试验研究[D].成都: 西南交通大学土木工程学院,2008.
[9]熊震威,谢铠泽,刘浩,王平.列车制动对刚构桥上无缝线路梁轨相对位移的影响研究[J].铁道标准设计,2013(10):10-14.
[10]中华人民共和国铁道部.铁建设函[2003]205号新建铁路桥上无缝线路设计暂行规定[S].北京: 中国铁道出版社,2003.
[11]易思蓉.铁路选线设计[M].成都: 西南交通大学,2009:57-58.
[12]颜乐,熊震威,魏贤奎,王平.坡度对长大坡道桥上无缝道岔的影响分析[J].铁道标准设计,2013(9):33-36.
[13]王平,郭利康.线路爬行对无缝道岔受力与变形的影响分析[J].西南交通大学学报,2002(12):615-619.
Feasibility Analysis of Seamless Turnout on Long Steep GradeZhang Meng-nan, Yan Le, Wang Ping, Wang Jian
(MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China)
Abstract:Based on the finite element method, this paper establishes a nonlinear resistance calculation model of the seamless turnout and analyzes rail longitudinal force and displacement under different working conditions. The results show that slope is negative to stress and deformation of seamless turnout. With the increase of the distance from the resistance reduced section to the turnout, the rail longitudinal force and the maximum displacement increase, and relative displacement between the point rail and the stock rail decreases. The decrease of track bed longitudinal resistance caused by insufficient tamping of track bed may significantly increase stress and deformation of each part of the turnout. Recommendation: (1) in a long steep grade area, the full-length quenched rail or high strength rail should be adopted; (2) observation pile should be arranged to look for turnout creeping where frequent braking is applied in front of the approach turnout, at the point of the seamless turnout, the frog heel and frog center; (3) anti-creeping of seamless turnout should be strengthened; (4) the thickness of the track bed in uphill direction should be increased and tamping reinforced.
Key words:Long steep grade; Seamless turnout; Finite element method; Nonlinear resistance
中图分类号:U215.5+7
文献标识码:A
DOI:10.13238/j.issn.1004-2954.2015.02.004
文章编号:1004-2954(2015)02-0013-04
作者简介:张梦楠(1990—),女,硕士研究生,E-mail:407809236@qq.com。
收稿日期:2014-04-30; 修回日期:2014-06-07

