基于生存资料探讨Ⅱ／Ⅲ期无缝设计靶向人群选择策略研究*

南京医科大学流行病与卫生统计教研室（210029） 缪丹丹 陈 峰 赵 杨 娄冬华 刘丽亚 于 浩

基于生存资料探讨Ⅱ／Ⅲ期无缝设计靶向人群选择策略研究*

南京医科大学流行病与卫生统计教研室（210029） 缪丹丹 陈 峰 赵 杨 娄冬华 刘丽亚 于 浩△

目的尽管对临床试验的数据进行事后分析可以鉴别出有意义的亚组人群，但是，这往往需要额外的验证性试验，导致研发周期延长，成本增加。据此，本文提出在无缝试验的设计阶段既考虑全人群效应也考虑亚组效应，并对该试验设计方案的统计学性质（I类错误，检验效能）进行评价。方法采用两阶段无缝设计的思想，在一阶段结束后同时对替代指标无进展生存期及主要研究总生存期指标进行期中分析，判断是只有亚组、只有全人群或两者均进入下一阶段的研究。二阶段结束后，采用Fisher法合并两个阶段的信息对主要研究指标OS进行最终的分析。结果观察OS与PFS不同相关程度下对总I类错误的影响，结果显示I类错误均能控制在0．025以内；不同情境下做出正确选择的概率均较高，试验结果与现实接近。结论在肿瘤临床试验中，若事先已存在某个亚组人群疗效更好的假设，且能通过一定的方法筛选出这些亚组人群，则可采用本文提出的试验设计方案，达到缩短临床试验周期、降低研究成本的目的。

靶向人群 Ⅱ／Ⅲ期无缝设计 Fisher合并 期中分析 时依终点指标

近年来，随着人们对于个体化医学及靶向治疗关注度的增加，临床试验中亚组人群的分析也变得很重要［1］。尤其是在肿瘤药物的研发过程中，越来越多的靶向药物得到认证［2－3］。例如2011年埃罗替尼的临床试验发现在晚期非小细胞肺癌人群中只有EGFR表达阳性的人群中才能得到有意义的结果［3］。尽管通过临床试验的数据可以进行事后分析以鉴别出有意义的亚组人群，但是往往还需要一个额外的验证性的试验，导致研发周期延长，成本增加。

因此有人提出了将适应性Ⅱ／Ⅲ期无缝设计（adaptive phase II／III seam less design，ASD）的思想用于肿瘤靶向药物的研发［1，4－8］。适应性Ⅱ／Ⅲ期无缝设计将传统的Ⅱ、Ⅲ期临床试验合并为一个完整的确证性试验，期间无空白间隙［9］。已有研究表明，正确利用该试验设计可以达到缩短研发周期、减少受试者人数、节约研究成本的目的［10］。目前采用这种设计进行靶向人群选择的有Friede以及Jenkins等人［5－6］。Jenkins提出期中分析时用替代指标（PFS）的风险比进行期中判断决策，采用封闭性准则来控制I类错误；Friede提出用条件误差函数来进行期中分析决策。

方法与原理

为方便起见，本文以肿瘤治疗中靶向药物为例。靶向药物研究中，会事先设定一个感兴趣的亚组，这个亚组可以通过生物标记物或者临床标准等来确定。在设计阶段，同时考虑全人群的效应及靶向人群的效应，根据第一阶段（即初始探索性阶段）数据进行期中分析，在此基础上来判断第二阶段的研究是用全人群，还是选择亚组人群继续进行试验，同时对第一阶段的人群保持随访；二阶段即确证性研究，根据期中分析结果纳入新受试者。

在肿瘤临床试验中，OS通常是金标准的评价指标，但是该评价指标往往需要很长时间的随访才能得到，因此本文考虑采用PFS替代OS来指导期中分析的决策分析，但是第二阶段结束后仍然用OS来进行最终的分析。本文在期中分析时用OS来判断是否有效终止，用PFS来判断是否无效终止，综合利用了OS和PFS的信息，使得信息的利用率得到提高。

这里每个人群都对应一个原假设：试验组与对照组OS无差别，分别记为（F为全人群，T为靶向人群），相应的备择假设为：试验组OS高于对照组，分别记为每一阶段对OS进行假设检验所得到的P值分别记为表示第一、二阶段。期中分析时两个人群根据OS与PFS信息所计算的p值分别记为

对于I类错误的控制借用成组序贯α消耗的思想，按照样本量将总α（0．025）分配给全人群和靶向人群。两个阶段α根据事件数进行分配，作为有效终止的界值，见公式（1），其中t为信息时间，是期中分析时发生的事件数与计划最终分析时总事件数之比。用Fisher合并检验［11］法计算无效终止界值，及最终合并检验的界值。

最终分析比较的界值计算见公式（2）。

期中分析时无效终止界值计算见公式（3）。

表1 第二阶段不同设计下合并分析统计量的计算

完整的流程图见图1。

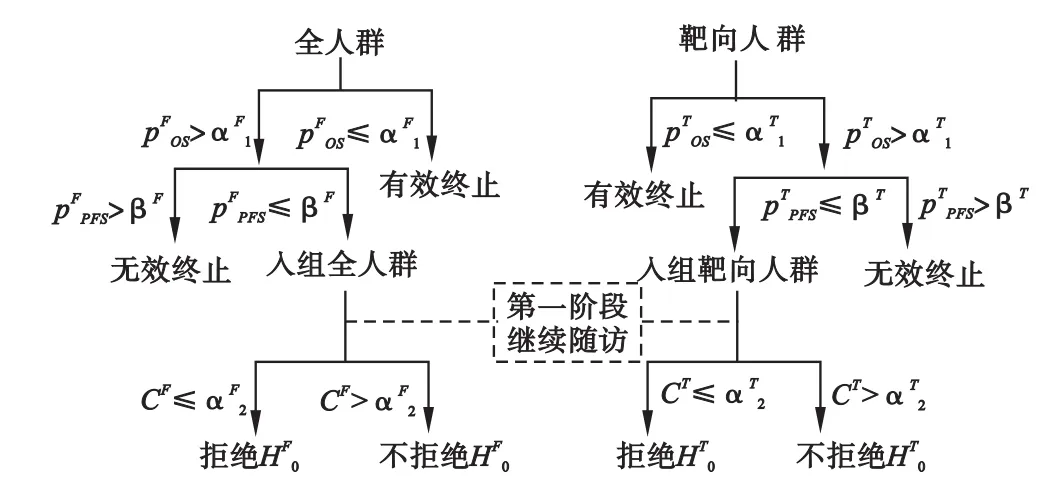
图1 试验设计流程图

模拟试验结果

通过模拟试验验证不同参数设置下对本试验设计的I类错误及检验效能的影响。

1．参数设置：

（1）基于二元指数分布［14］产生模拟试验所需数据；

（2）研究对象的入组时间假定服从均匀分布；

（3）一阶段全人群样本量为300，靶向人群比例分别考虑0．2，0．4，0．6，0．8；

（4）二阶段针对全人群进行分析或者Co-primary分析样本量为800；针对靶向人群分析的样本量为400，根据设定的两个人群的不同风险比计算样本量，选取最大的样本量；

（5）期中分析时间点发生200个PFS事件；

（6）最终分析时间点为一阶段、二阶段分别有250个、500个受试者发生死亡事件；

（7）总I类错误为0．025，按照靶向人群所占样本量比例进行分配，根据上文的计算方法得到的具体界值见表2；

（8）模拟次数参考其他文献设为3000次。

表2 靶向占不同比例期中分析与最终分析界值

2．模拟试验结果

（1）I类错误

表3为PFS及OS不同相关程度下对总I类错误与两个阶段p值之间相关的影响。总I类错误定义为零假设下即全人群与靶向人群风险比均为1的情况下，拒绝至少一个原假设的概率。这里不考虑有效终止及无效终止，即试验第二阶段既考虑全人群也考虑靶向人群的效应。没有提前终止意味着由于多重比较造成的保守，如果允许提前终止则I类错误率会降低。

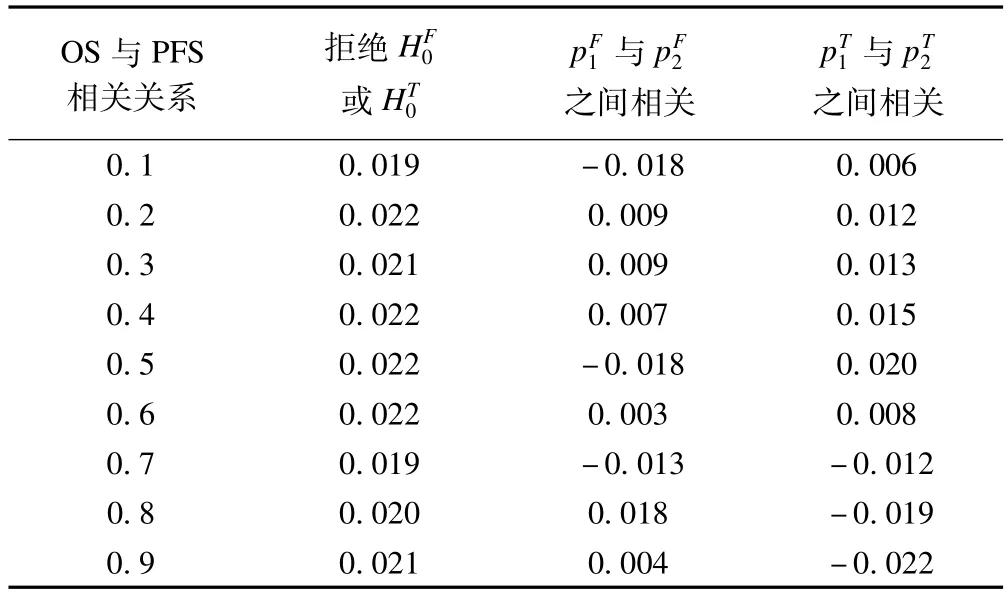
表3 OS与PFS不同相关下对I类错误的影响

从表中可以看出I类错误率都控制在0．025以内。两个阶段p值之间的相关系数都在0．05以内，说明了两个阶段数据之间的独立性，从而为最终分析使用Fisher合并原则提供依据。

表4为不同靶向人群比例对I类错误的影响，此时考虑了提前终止试验。结果显示，I类错误都控制在0．025以下（约0．02）。相比于表2的结果，由于允许提前终止试验，I类错误稍有下降。可以看出无效终止概率达到30%，这样可以有效地提前终止试验，节约样本量及时间。

（2）检验效能

表5是不同参数设置下对于本试验设计检验效能的影响。这里的检验效能不是条件概率，而是指在不同的备择假设下做出正确的期中分析及最终分析决策的概率，即总的拒绝的概率，包括提前有效终止的概率。

表4 靶向人群不同比例对I类错误的影响（重复次数＝3000）

表5 不同参数设置对效能的影响

情境一是PFS及OS指标靶向人群有效，非靶向人群无效，其中靶向人群的风险比为0．6。从结果可以看出靶向人群的比例对检验效能有明显的影响。随着靶向人群比例的增加，总效能增加，这是由于其使得全人群的效应增加；同时全无效终止（即靶向人群无效，全人群也无效终止）的比例逐渐降低，全有效终止的比例逐渐增加，第二阶段仅有靶向人群的比例逐渐降低。当靶向比例很高，比如达到80%时，同时拒绝的概率很大。因此如果只想得到靶向有效的结论，则靶向人群应与全人群的效应相差很大且靶向占的比例很小。

情境二是PFS及OS两个指标靶向及全人群均有效且疗效相等，风险比均为0．7。可以看出总效能相较于情境一有所提高。全无效终止的概率相较于情境一降低；进入第二阶段后约有50%的概率既考虑全人群效应也考虑靶向人群效应，在此种情况下最终分析同时拒绝两者的概率大于单独拒绝全人群或者单独拒绝靶向人群的概率；第二阶段仅考虑全人群效应比仅考虑靶向人群效应的概率大，当第二阶段仅考虑全人群效应时有大于90%的概率拒绝全人群所对应的假设；靶向所占比例的影响没有情境二那么明显。

情境三靶向人群PFS与OS指标的风险比分别为0．5、0．6，非靶向人群分别为0．7、0．8，此时靶向与非靶向人群均有效，但靶向人群的效应高于非靶向人群。结果与情境二的结果类似，与其相比总效能、全有效终止的概率升高，全无效终止的概率降低；第二阶段最常见的是既考虑全人群也考虑靶向人群的效应，此时两者都被拒绝的概率大大增加；当第二阶段仅有靶向人群时拒绝靶向人群假设的概率降低。

情境四是靶向人群有效，非靶向人群与其有相反的效果，且PFS的效应高于OS，靶向人群PFS与OS风险比分别为0．5、0．6，非靶向人群分别为2、1．7。结果显示总效能低于情境三，仅靶向有效终止的概率先增大后随着靶向比例的增加而减少；当靶向比例较小时第二阶段几乎只纳入靶向人群，仅考虑靶向人群的效应，且通常拒绝靶向人群对应的假设。随着靶向比例的增加，全人群的效应得到增强，因此第二阶段Coprimary的情况逐渐增多，且同时拒绝全人群及靶向人群的概率增加。

综上所述，采用本文提出的实验设计可将I类错误控制在0．025以内，不同情境下检验效能较高，试验结果与实际情况接近。

讨 论

适应性设计的提出使得药物研发过程变得更加灵活高效，但同时也会增加设计和分析的复杂性，以及其他方面的困难。在应用适应性Ⅱ／Ⅲ期无缝设计时需考虑的一个问题是在二阶段入组前能够得到可靠的一阶段的相应指标的信息，以保证在大规模的III期试验之前作出正确的决定。也就是说除非有指标能够短期内得到结果，否则适应性设计并不显示其优越性。

本文是关于适应性Ⅱ／Ⅲ期无缝设计的一个扩展研究，期中分析同时考虑主要终点指标及替代指标进行决策，并通过模拟试验说明了这些改变包括同时考虑两个假设以及利用两种指标等不会造成I类错误的膨胀，最重要的是模拟试验的结果与参数设置的现实情况是相似的，且通过试验得出当靶向人群及全人群都有效的情况下，不论OS与PFS之间疗效的大小关系，效能都能达到预先设定的把握度。

本文的试验设计前提是已经存在一个“在特定的包括亚组人群上疗效更好的”假设，且这个亚组可以通过生物标记物或者临床界值等鉴别出来。因此在试验之前已经有了固定的假设，这个假设可以来源于I期的试验。在实际的临床试验中，若可以通过I期的试验得到某个人群可能有效的信息，则II期及III期的试验设计可参照本文的设计进行。

本试验设计仅涉及到生存指标，但易拓展到其他类型的指标，也可设置为多个亚组，但是当存在多个亚组且亚组结果之间存在相关时会使得试验变得更复杂，有待于进一步讨论。

［1］Stallard N，Hamborg T，Parsons N，et al．Adaptive designs for confirmatory clinical trials with subgroup selection．J Biopharm Stat，2014，24（1）：168-187．

［2］Hegi ME，Diserens AC，Gorlia T，et al．MGMT gene silencing and benefit from temozolom ide in glioblastoma．N Engl JMed，2005，352（10）：997-1003．

［3］BruggerW，Triller N，Blasinska-Moraw iec M，et al．Prospectivemolecularmarker analyses of EGFR and KRAS from a random ized，placebo-controlled study of erlotinib maintenance therapy in advanced non-small-cell lung cancer．JClin Oncol，2011，29（31）：4113-4120．

［4］Stallard N．Group-sequentialmethods for adaptive seam less phase II／III clinical trials．JBiopharm Stat，2011，21（4）：787-801．

［5］Brannath W，Zuber E，Branson M，et al．Confirmatory adaptive designs with Bayesian decision tools for a targeted therapy in oncology．Stat Med，2009，28（10）：1445-1463．

［6］Jenkins M，Stone A，Jennison C．An adaptive seam less phase II／III design for oncology trials with subpopulation selection using correlated survival endpoints．Pharm Stat，2011，10（4）：347-56．

［7］Ye Y，Li A，Liu L，et al．A group sequential Holm procedure with multiple primary endpoints．Stat Med，2013，32（7）：1112-1124．

［8］Friede T，Parsons N，Stallard N．A conditionalerror function approach for subgroup selection in adaptive clinical trials．Stat Med，2012，31（30）：4309-4320．

［9］Bretz F，Schm idli H，König F，et al．Confirmatory seam less phase II／III clinical trials with hypotheses selection at interim：general concepts．Biom J，2006，48（4）：623-634．

［10］Schm idli H，Bretz F，Racine A，et al．Confirmatory seam less phase II／IIIclinical trials with hypotheses selection at interim：applications and practical considerations．Biom J，2006，48（4）：635-643．

［11］Chang M．Adaptive design method based on sum of p-values．Stat Med，2007，26（14）：2772-2784．

（责任编辑：郭海强）

The Strategy for Selecting Target Population Using Adaptive Phase II／III Seam less Design Based on Time-to-event Data

M iao Dandan，Chen Feng，Zhao Yang，et al．（DepartmentofEpidemiology＆Biostatistics，NanjingMedicalUniversity（210029），Nanjing）

ObjectiveAlthough subgroups can be identified on the basis of post-analysis，it needs an additional confirmatory trial and thismay lead to an inflation in development time and cost．We presentan approach that view treatment comparisons in both a predefined subgroup and the full population in the design period of a seam less trial，then evaluate the statistical characteristics．MethodsIt is based on the adaptive phase II／IIIdesign．The decision of continuing seam lessly either in a subgroup or the full population is on the basis of analysis of PFS and OS obtained from the first stage．Final analysis is conducted only for OS using Fisher combinationmethod after the second stage trial．ResultsIt is shown that the type-I-error rate is less than 2．5%and is independentof the correlation of OS and PFS．The simulations demonstrate that correct conclusions are reached sufficiently often in the various scenarios．ConclusionIn oncology trials if there is an priorihypothesis about increased efficacy in a defined subgroup and this subgroup can be well characterized，our design can shorten the time and cost．

Subgroup selection；Adaptive seam less phase II／III design；Fisher combination test；Interim analysis；Timeto-event endpoint

*：国家自然科学基金（81273184）

△通信作者：于浩，E-mail：haoyu＠njmu．edu．cn