矩阵方程AX-BY=Z反问题的广义中心对称最小二乘解

冷　晔

(九江职业大学　江西九江　332000)



矩阵方程AX-BY=Z反问题的广义中心对称最小二乘解

冷晔

(九江职业大学江西九江332000)

摘要：文章研究矩阵方程AX-BY=Z反问题广义中心对称最小二乘解，给出了AX-BY=Z的最小二乘广义中心对称解的表达式，导出了AX-BY=Z有广义中心对称解的条件.讨论了在AX-BY=Z的最小二乘广义中心对称解集合中求与给定矩阵最佳逼近的解的问题.

关键词：矩阵方程，广义中心对称矩阵，最小二乘，最佳逼近，反问题

矩阵方程是科学与工程计算与数值代数的重要研究内容之一[1-4].而中心对称矩阵在信息论、线性系统理论、线性估计理论以及数值分析等领域有着重要应用[1].对中心对称问题的若干问题的研究取得了一些有意义的成果，如文献[2]给出了矩阵方程AX ? BY = Z的最小二乘中心对称解及其最佳逼近，文献[6]研究了一类二次特征值反问题的中心对称解及其最佳逼近问题.广义中心对称矩阵是中心对称矩阵的推广， 在工程与科学计算等领域已得到了广泛的应用[3].

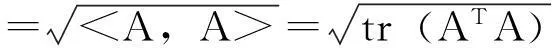
记ei为n阶单位矩阵In的第n列，取Sn=(en,en-1,…,e1)，显然，Sn是对称正交阵.

定义1：设P,Q分别是给定的n阶和m阶对称正交矩阵，如果A∈Rn×m满足A=PAQ，则称矩阵A为关于P,Q的广义中心对称矩阵，所有n×m广义对称矩阵的全体记为Rn×m(P,Q)

显然，矩阵集合Rn×m(P,Q)与P,Q有关，当P=Q=Sn时，集合Rn×m(P,Q)就是熟知的中心对称矩阵集合，全文假定P,Q时给定的.

本文讨论如下问题：

问题I：给定X,Y∈Rm×p,Z∈Rn×p，求A,B∈Rn×m(P,Q)使‖AX-BY-z‖=min.

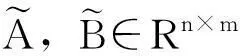
1问题I的解

由于P,Q均是对称正交矩阵，所以P,Q的特征值是1或-1，而P,Q分别正交相似于对角矩阵，故不难证明下面引理：

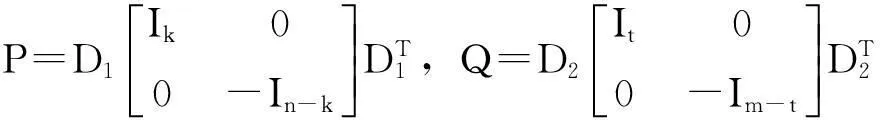
(1)

其中，D1∈ORn×n,D2∈ORm×m.

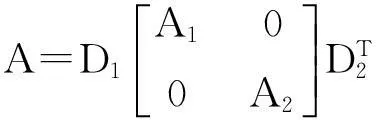
(2)

(3)

其中，A1,B1∈Rk×t,A2,B2∈R(n-k)×(m-t).

证明：先对矩阵A进行证明：

假设A∈Rn×m(P,Q)，有A=PAQ，由式(1)得：

(4)

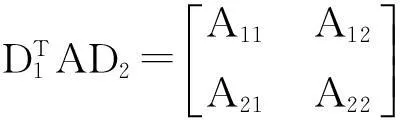
(5)

其中，A11∈Rk×t,A22∈R(n-k)×(m-t)，将(5)代人(4)比较知A12=0,A21=0因此A可以表示为式(2).反之，对于任意A11∈A22∈R(n-k)×(m-t)，考虑到D1,D2都是正交矩阵，有：

同理对矩阵B进行证明.

引理3：设X,Y∈rm×p,Z∈Rn×p，则集合S={A,B∈Rn×m|‖AX-BY-Z‖=min}的任意解可以表示为：

(6)

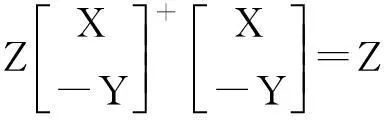
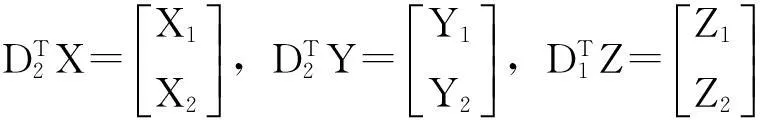
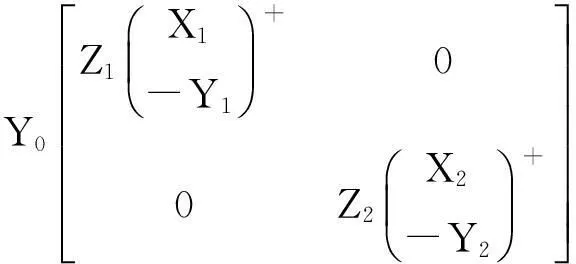
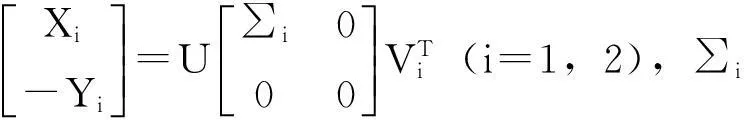
Vi=，[Vi1Vi2]∈ORp×p，Vi1∈Rp×si则问题I的广义中心对称解为：

(7)

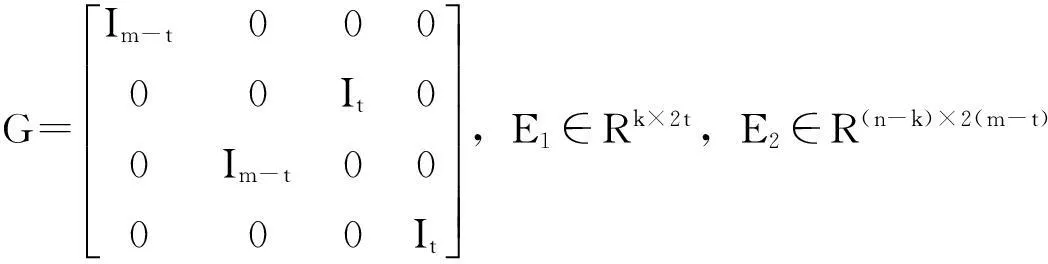
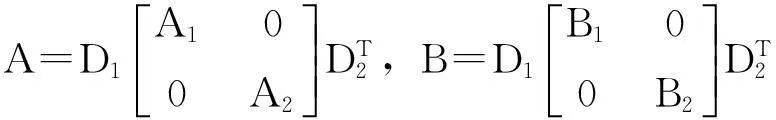
‖AiXi-BiYi-Zi‖=min

(8)

由引理3可得(7)的解为：

(9)

其中，E1∈Rk×2t,E2∈R(n-k)×(m-t)是任意矩阵，因为

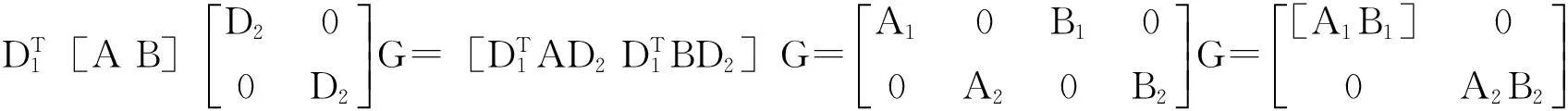
因为AX-BY=Z有解A,B∈Rn×m(P,Q)当且仅当AiXi-BiYi=Zi(i=1,2)有解，则由引理3可得如下结果：

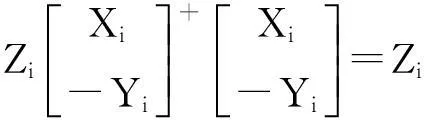
2问题II的解

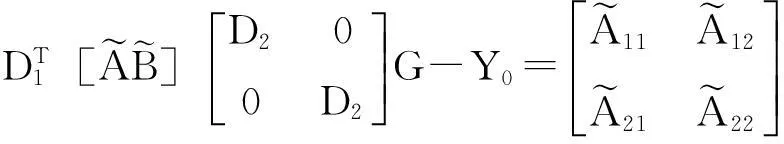
SAB=

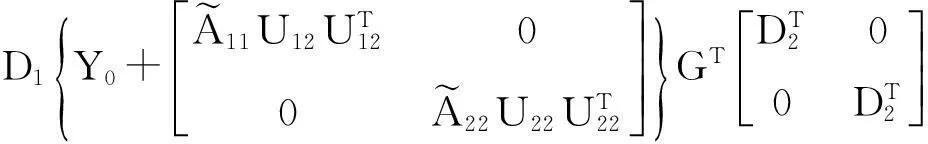
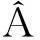
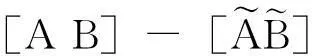
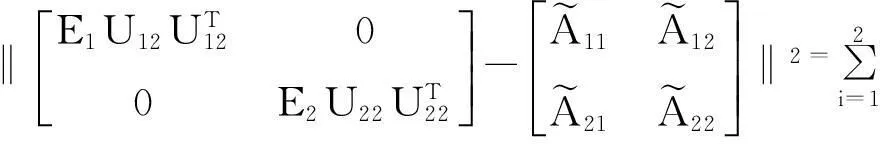
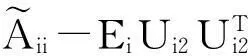
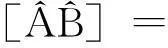
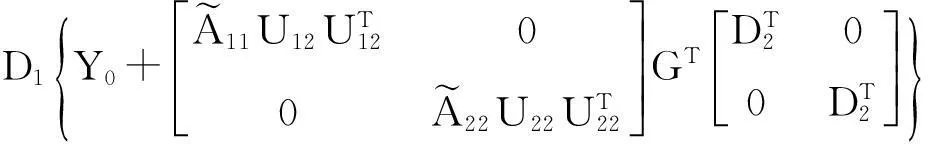
(2)计算D1,D2,X1,X2,Y1,Y2,Z1,Z2；

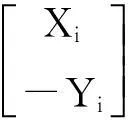
(4)输入G，并计算Y0；

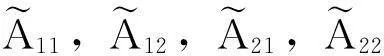
3计算示例

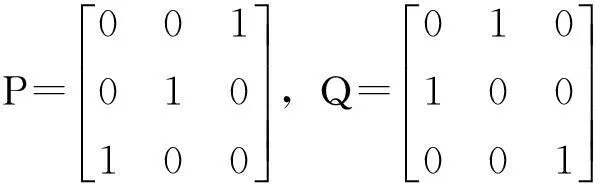
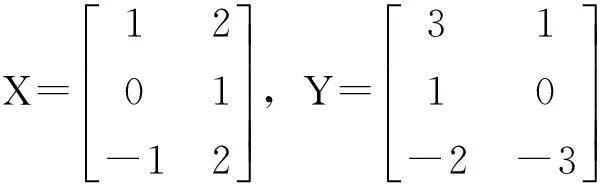
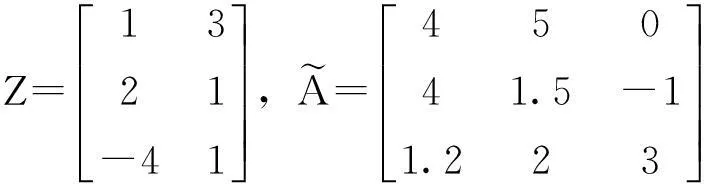
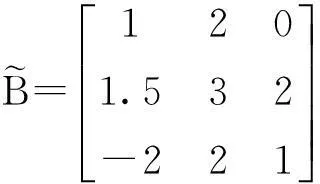
通过用“Matlab”计算，可得到问题Ⅱ的解为：

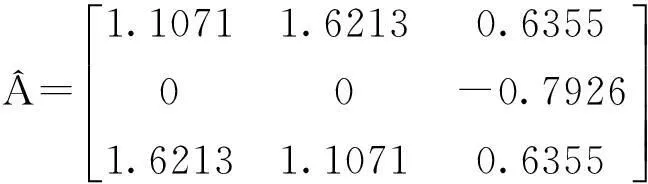
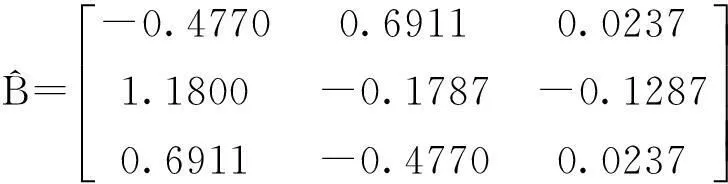
参考文献：

[1]戴华.矩阵论[M].北京：科学出版社，2001.69.

[2]桂冰，戴华. 矩阵方程AX-BY=Z的最小二乘中心对称解及其最佳逼近[J].工程数学学报，2006，23(5):849.

[3]肖庆丰，胡锡炎.广义中心对称矩阵反问题的最小二乘解[J].数学实践与认识，2010，40(16)：217.

[4]ZY Peng. The inverse problem for Hermitian anti-reflexive matrices and its approximation[J]. Math Comput，2005，162(3)：1377.

[5]YX Yuan. Least squares solutions of matrix equation AXB = E，CXD = F[J]. Journal of East China Shipbuilding Institute (Natural Science Edition)，2004，18(3)：29.

[6]桂冰，戴华.一类二次特征值反问题的中心对称解及其最佳逼近[J].数学学报，2006，28(4)：367.

(责任编辑李佳瑜)

中图分类号：0241.6

文献标识码：A

文章编号：1674-9545(2015)04-0087-(04)

通讯作者：冷晔，670449611@qq.com.

收稿日期：2015-10-10