SAM-GN联合算法及其在超声回波参数估计中的应用

武良丹　郭　涛

(九江学院电子工程学院　江西九江　332005)



SAM-GN联合算法及其在超声回波参数估计中的应用

武良丹郭涛

(九江学院电子工程学院江西九江332005)

摘要：针对传统高斯牛顿法在估计超声回波参数时初值设置问题及局部搜索问题，提出一种基于高斯牛顿法和模拟退火算法的改进算法——SAM-GN联合算法。该算法充分利用模拟退火的全局搜索能力和高斯牛顿法的局部快速搜索的优点，解决了高斯牛顿法对初值敏感问题及易陷入局部最优的问题。仿真结果表明，基于SAM-GN算法具有对初值不敏感，且精度高的特点。

关键词：高斯回波模型，参数估计，SAM-GN联合算法

超声回波信号中包含了超声换能器的脉冲响应及传输路径的各种信息，可以利用模型化的方法对超声回波进行分析和估计，通过对模型参数的分析，可以得出一些关于目标及传输路径的一些信息，如何精确的计算超声回波参数对于超声无损检测就显得十分重要。

2001年，Demirli等除了超声散射回波的非线性模型和参数估计方法[1]，该模型包括了超声的到达时间、信号的中心频率、振动幅度和相位等参数，后人将高斯牛顿、能级遗传优化、时频分析方法、蚁群优化算法等优化方法应用于超声回波的估计中，但仍然存在回波参数精度不高或依赖初始值或已陷入局部最优解等缺点[2]。针对这些问题，文章提出基于模拟退火法和高斯牛顿法的SAM-GN联合算法，解决了依赖于初始值以及局部收敛等缺点，且估计出的参数精度高。

1SAM-GN联合算法

SAM-GN联合算法是基于模拟退火法和高斯牛顿法而提出的新算法。该算法综合了模拟退火法和高斯牛顿法的优点，具有全局搜索能力强，不依赖与初值且精度高的优点。

模拟退火算法源于对固体退火过程的模拟，该算法求解组合优化问题的思路如下：由初始解X(0)和控制参数初值开始，对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代，并逐步缓慢衰减t值，算法终止时当前解近似为所得到最优解。退火过程由参数的初值t(0)，衰减因子Δt，每个t值时迭代次数L和停止条件等冷却进度表参数控制。该算法能以一定的概率接受恶化解，所以能挑出局部最优解，最终收敛于全局最优解。高斯牛顿法具有计算精确的优点。SAM-GN联合算法即先通过模拟退火算法计算出大致的参数，再将该计算出的参数作为高斯牛顿法的初始值，由于高斯牛顿法的计算速度快，并不会引入太大的时延，而高斯牛顿法利用二阶求导的方法能够较为精确的计算出参数。

2高斯回波模型

超声换能器的脉冲响应可以模拟成高斯回波[1]：

x(t)=e-at2cos(2πfct)

(1)

实际超声检测中，通过换能器测得的信号是N重背向散射回波的叠加：

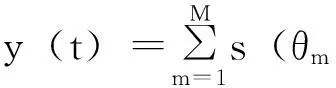
(2)

其中：v(t)为的高斯白噪声(WGN)，θm为第m个参数向量。

单个高斯回波的一般模型为：

s(θ；t)=βe-α(t-τ)2cos{2πfc(t-τ)+φ}

(3)

式中参数向量θ=[α τ fcφ β]为超声回波中的特征参数向量，其中α为带宽因子，τ为当前回波的到达时间，fc为中心频率，φ为回波相位，β为回波幅度系数。若能精确计算出超声回波的系数，则能有效的抑制噪声并提取出相应的信息。

3SAM-GN联合算法步骤

3.1 构造函数

应用最小二乘法构造函数：

N为一个周期离散点数，x为实际中测得的超声回波数据，s(θ(k))为第k次利用高斯回波模型模拟出的函数向量。

3.2SAM-GN联合算法具体流程

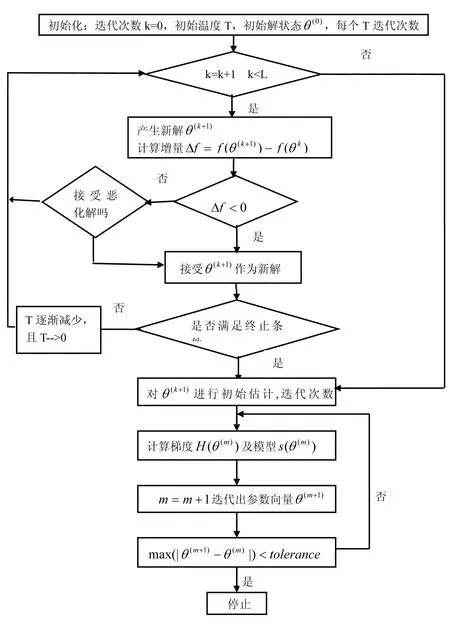
图1是SAM-GN的联合算法流程图，几点说明如下：

(1)根据Metropolis准则，初始迭代时的接收概率p=e-Δf/T≈1；

(2)新解的产生：x(new)=x+r·scale·x，其中r为0～1间的随机数，scale限制了新解的变化范围，本文中scale为0.002；

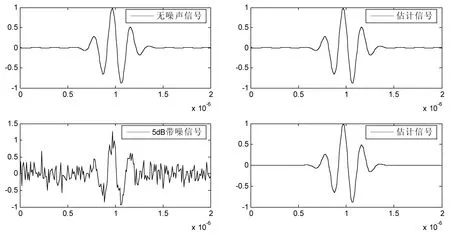
(3)是否接收恶化解，是先产生一个0～1之间的随机数p，若满足p

图1SAM-GN算法流程4SAM-GN联合算法在超声回波模拟参数估计中的应用

(4)第一阶段的终止条件是达到一个很小的T，或者2～10个相继的Mapkob链中的解无任何变化。

若真实参数α=25MHz，τ=1μs，fc=5MHz，φ1rad，β=1，采样频率为200MHz，设置初始值为α=14MHz，τ=0.7μs，fc=3MHz，φ0.6rad，β=0.7。参数估计结果详见表1。

表1　参数估计结果

图1无噪声和信噪比为5dB时原始波形及估计波形

从表1可以看出，当设置初始值举例真实值较远的情况下，在无噪声的情况下，几乎是可以精确的估计出真实的参数向量，依次加入20dB、10dB、5dB的高斯白噪声，利用SAM-GN算法，仍然能较为精确的估计出参数向量，相比文献[4]，当初始值设置距真实值较远时，高斯-牛顿法不能估计出参数，而单纯的模拟退火算法虽然能估计出参数，但参数的精度相比SAM-GN联合算法要差得多。无噪声和信噪比为5dB时原始波形及估计波形如图1所示。

图1绘出无噪声以及信噪比为5dB情况下的原始信号及根据SAM-GN联合算法计算出参数后的估计波形。从图上可以看出，无噪声情况下，估计波形和原始波形没有误差，信噪比为5dB情况下，估计出的波形仍然与无噪声信号相似，误差很小。

5结论

超声回波参数估计是超声检测中的一个重要课题，文章提出的SAM-GN联合算法相比单纯的高斯-牛顿法而言具有初值设置范围广，对初值设置不敏感，具有全局收敛的特点。该算法与单纯的模拟退火算法相比，估计出的回波参数更加精确。由于该算法是全局收敛的，故运行时间较长，在后续的研究中，可以通过不断地改进步长增长等缩短搜索时间。

参考文献：

[1]Hgglund F， Martinsson J， Carlson JE. Model-based estimation of thin multi-layered media using ultrasonic measurements[J]. IEEE Trans Ultrason Ferroelectr Freq Control，2009，56(8)：1689.

[2]周芳，张小凤，张光斌，等.蚁群算法中参数设置对超声回波估计性能的影响[J].中国科学：信息科学，2013，5(2)：243.

[3]康立山，谢云等.非数值并行算法—模拟退火算法(第一册)[M].北京：科学出版社，2003.35.

[4]武良丹，张小凤，何西平.基于模拟退火算法的超声回波参数估计[J].应用声学，2007，26(5)：313.

(责任编辑李平)

中图分类号：O 426.4

文献标识码：A

文章编号：1674-9545(2015)04-0037-(03)

通讯作者：武良丹，wuliangdan82@163.com。

收稿日期：2015-10-1