单脉冲雷达速度量折射误差高精度修正方法

张 瑜 史莹莹 张洁寒

（1.河南师范大学物理与电子工程学院，河南 新乡453007；2.西安电子科技大学电子工程学院，陕西 西安710071）

引 言

在对空中飞行体的测量中，单脉冲雷达是一种大量应用的主要测量设备之一，它可以较精确地测量出目标的位置参数（距离、仰角和方位角）和速度量（距离变化率）.单脉冲雷达一般为主动式有源雷达，它利用电磁波的散射来实现目标的参数测量.当电磁波在大气中传播时，由于大气介质对电磁波的折射效应，使得雷达测量时产生折射误差，从而影响雷达的测量精度［1-2］.随着目前数字技术的应用，尽管雷达系统在硬件和数据处理方法上得到了进一步改进，使得其测量精度得到了一定的提高，但是大气引起的折射误差仍然是限制雷达精度进一步提高的关键因素之一.为了提高雷达测量精度，需要进行大气折射误差修正.

国内外许多学者针对不同体制雷达，如光学雷达、脉冲雷达、连续波雷达、干涉仪等，都进行了各种电波折射误差修正方法研究［3-8］，这些方法大多数已在实际中进行了应用，并取得了较好的效果.然而，绝大多数电波折射误差修正工作都仅仅考虑了大气折射对雷达定位的影响，很少考虑雷达测量的速度量折射误差.我们知道，对飞行体的速度量测量也是判定其状态的一个重要参量，大气折射效应不仅会引起雷达定位误差，也会引起测速误差，因此对于速度量也需要进行折射误差修正.

文献［5］只给出了三个及以上雷达站联合测量时的速度量折射误差修正方法，没有给出单站雷达的速度量折射误差修正方法.以文献［8］为代表的有关文献尽管给出了单站雷达速度量折射误差修正方法，但是他们都是仅用距离变化的时间差分来进行速度折射误差估算，这也是目前单站雷达进行速度量折射误差修正的主要方法.然而在实际应用中，由于这种方法只是根据距离折射误差的时间差分来估算距离变化率的折射误差，受其距离折射误差残差和差分时间的限制，其精度很低.另外，在实际应用中，差分时间是根据雷达对信号的采样时间确定，差分时间对速度折射误差估算的影响很大，使得这种方法很难在实际中应用.本文针对单脉冲雷达这种实际应用现状，给出了基于方向余弦的速度量折射误差高精度修正方法.

1 常用目标定位与速度量折射误差算法

1.1 目标定位方法

假设雷达位置为O，目标位置为T，地球地心为C，雷达天线中心的海拔高度为h0，如图1所示.

鉴于平坦下垫面情况下的大气水平不均匀性很小，在实际应用中一般可不考虑方位角的折射误差，即A0＝Ae.

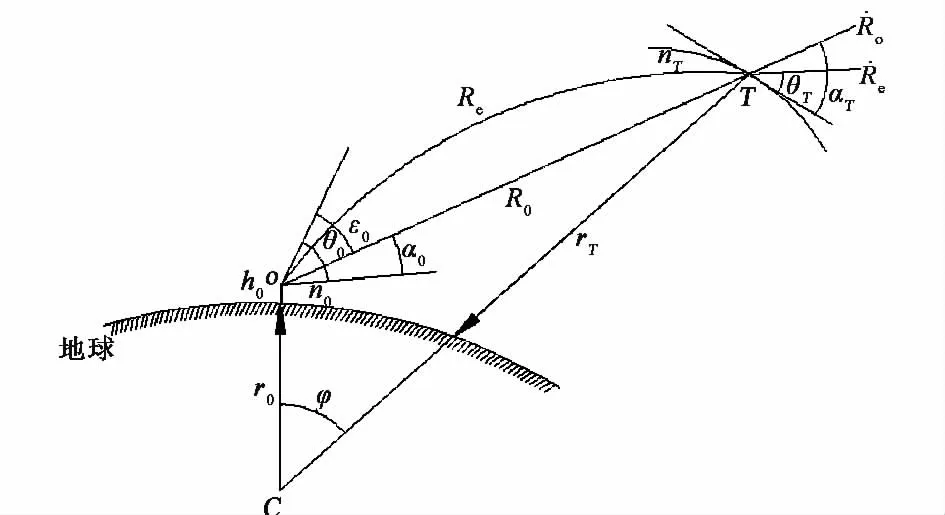
图1 雷达电波射线示意图

单脉冲雷达测量参数有：折射误差的视在距离Re、视在仰角θe、视在方位角Ae和视在距离变化率˙Re（它是速度在视在距离上的径向分量）.

利用文献［6］可对视在距离和视在仰角进行折射误差计算，从而获得距离折射误差ΔR和仰角折射误差ε.利用文献［9］可以对视在方位角进行折射误差计算，得到方位角折射误差ΔA.这样真实的距离R0、仰角α0和方位角A0为：

假设在一确定的坐标系中，雷达站的坐标为O（x0，y0，z0），根据几何关系，利用经电波折射误差修正后雷达测量的真实参数R0、α0和A0可以得到目标的真实位置坐标，即

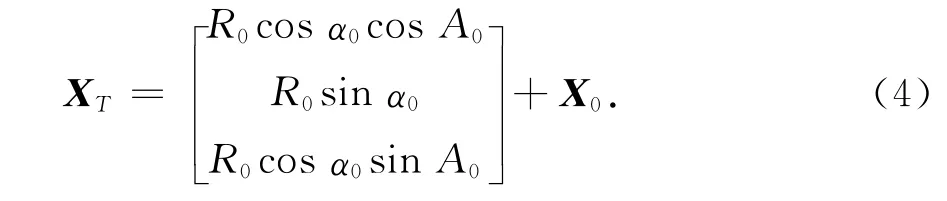
式中：XT为目标真实位置向量，XT＝（xT，yT，zT）T；X0为雷达站位置向量，X0＝（x0，y0，z0）T.

1.2 常用速度量折射误差算法

对于单脉冲雷达，目前的距离变化率折射误差计算是根据距离变化的微分得到的.根据物理意义，视在距离变化率和真实距离变化率为：

则距离变化率折射误差为

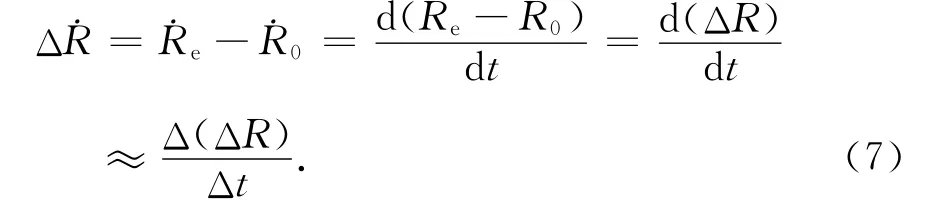
利用这种方法计算距离变化率的折射误差存在两个问题：其一是由于雷达的采样是离散数据，它只能用差分进行计算，而没法实现微分计算；二是时间差分Δt的微小变化对计算结果影响很大，再加上距离折射误差的残差影响，可能会使得到的距离变化率折射误差的残差很大，进而无法获得高精度的距离变化率折射误差，这一点在实际应用中已得到证实.因此，这种方法获得的速度量折射误差一般不能在实际中应用.

2 新型速度量折射误差修正方法

2.1 真实速度向量计算

从理论上讲，单脉冲雷达只有一个距离变化率参量，利用它无法得到目标速度的三个分量.在实际应用中，常采用二阶中心平滑微分方法来求得三个真实速度分量.即假设输入2n＋1个等间距采样的位置参数XTi（由式（4）得到，是经过折射误差修正后的位置参数），中心时刻的速度向量为［1］

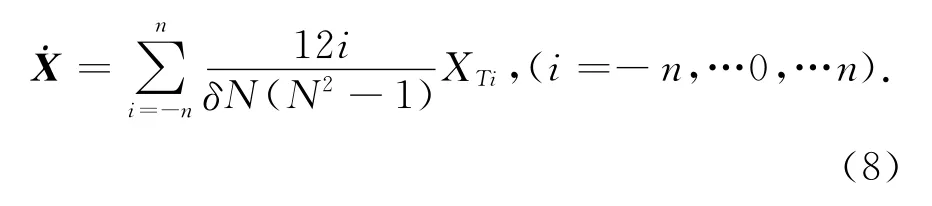
式中：δ为测量数据的采样间隔；N为输入数据的总个数，N＝2n＋1.

2.2 距离变化率折射误差修正

雷达测速的折射误差主要是由于折射效应改变了多普勒频率的传播方向而引起的，也就是由视在电波路径与真实路径不一致而产生.雷达视在电波路径是一个弯曲的曲线，它测量出的是视在距离变化率，雷达真实路径为一直线，由它得出的是真实距离变化率，如图1所示.

式中：nT为目标处的大气折射率，可由大气折射率分段模型计算得到；为目标的真实速度向量；LT0＝（l0，m0，n0）为目标与雷达站相连直线的方向余弦；LTe＝（le，me，ne）为目标与雷达站间电波射线（曲线）在目标T处切矢的方向余弦.

由于雷达站位置O（x0，y0，z0）、地心位置C（xC，yC，zC）和经电波折射误差修正后的目标真实位置T（xT，yT，zT）都为已知量，则目标与雷达站相连直线的方向余弦LT0＝（l0，m0，n0）为

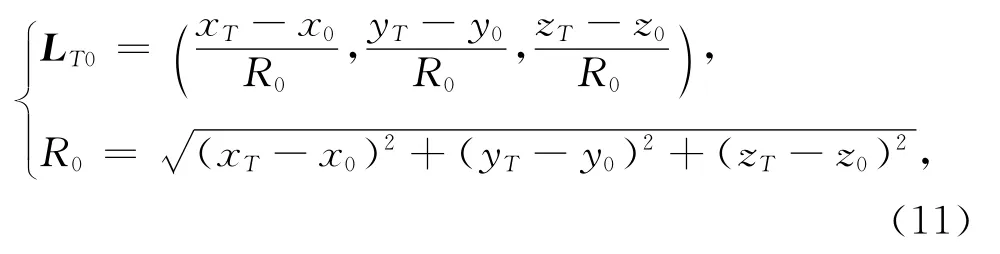
目标与地心相连直线的方向余弦LTC＝（lC，mC，nC）为

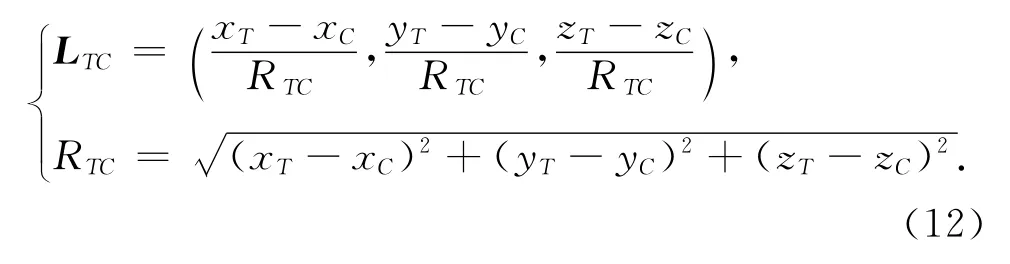
根据几何关系和相关推导可以得到目标与雷达站间电波射线在目标T处切矢的方向余弦LTe＝（le，me，ne）为［8］

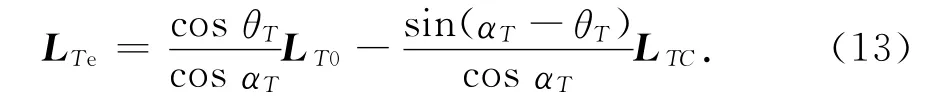
式中：θT为目标处的电波射线视在仰角；αT为目标处的电波射线真实仰角.

目标处电波射线视在仰角θT可根据球面分层大气情形下的snell定理得到［8］，即

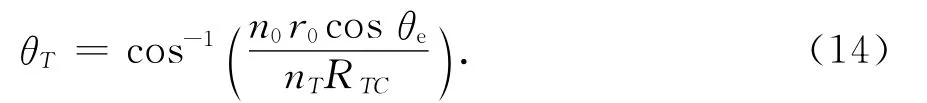
式中：n0、nT分别为雷达站、目标处的大气折射率；RTC为目标地心距；r0为雷达地心距，r0＝

目标处电波射线真实仰角αT可通过图1中的几何关系，用三角正弦公式得到，即

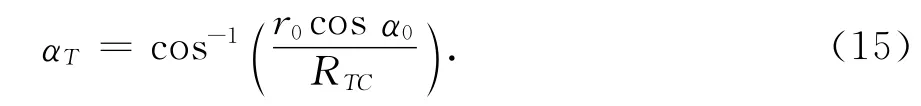
利用式（8）、（9）、（10）、（11）和（13）可以得到视在距离变化率和真实距离变化率，这样电波折射引起的距离变化率误差即为

3 仿真实验与结果分析

为了检验本文所提方法的正确性和有效性，选择了某雷达实验基地一次校飞时的相关数据进行距离变化率折射误差计算.试验中，可测量到的携带应答器的飞机高度为200～1 500m，飞行中飞机有一定高度上下起伏.根据本文的方法和利用式（7）选取差分时间分别为2ms和5ms进行计算，得到的距离变化率的折射误差如图2所示.

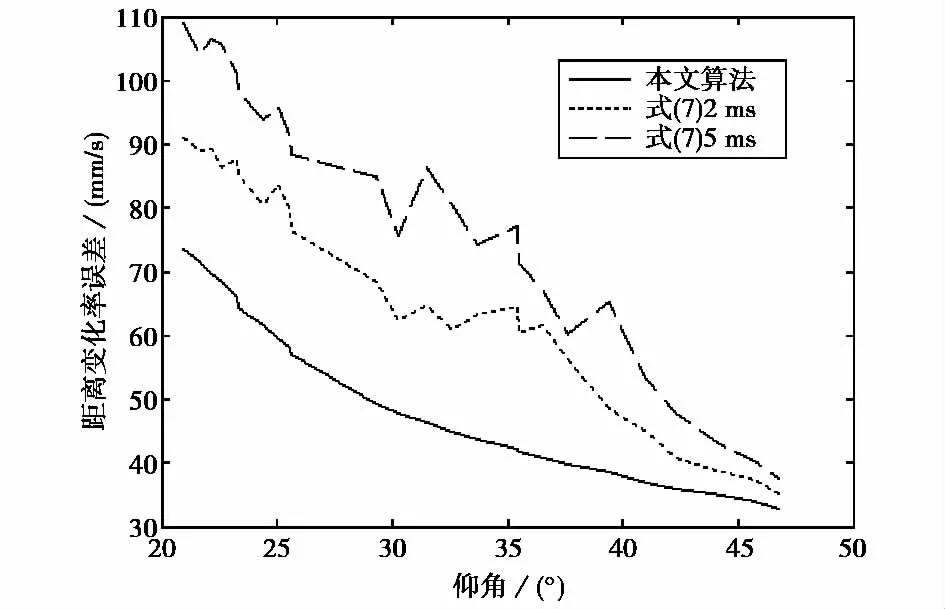
图2 两种方法计算的距离变化率折射误差比较

从两种方法计算距离变化率折射误差结果比较可见：1）距离变化率的折射误差随仰角的增大而逐渐减小，这是由于校飞的飞机基本上为平飞，且雷达测量的仰角越大，目标距离雷达的距离越小，电波射线经过的路径越小，电波射线弯曲越小的缘故.2）基于方向余弦的方法得到的距离变化率折射误差小，且随角度的变化平滑，符合真实情形.而基于距离折射误差微分的方法得到的距离变化率折射误差较大，且随角度呈跳跃状，与实际情形不相符合.这主要是由于距离折射误差的残差和所取差分时间较大所造成的.3）对比差分时间5ms和2ms时的计算结果可见，差分时间越大，得到的距离变化率折射误差越大，且抖动也越大，越不符合实际情形，说明差分时间对距离变化率折射误差的影响是很大的.如果在实际应用中采用距离折射误差微分的方法，这只能对计算得到的距离变化率折射误差进行数据平滑，或者尽量减小差分时间，但是这受限于雷达信号的采样时间.4）对比校飞实测数据，基于方向余弦方法得到的距离变化率折射误差的残差为11%，基于距离折射误差微分的方法（时间间隔分别为2 ms和5ms）得到的距离变化率折射误差的残差分别平均为31%和43%，说明基于方向余弦方法的精度比基于差分的方法高20%.因此，可以认为基于方向余弦的方法可以较好地进行距离变化率折射误差修正，且具有高精度和实用性.

4 结 论

为了提高单脉冲雷达的测量精度，对于测量的距离变化率利用常规的差分方法很难进行有效的折射误差修正.利用基于方向余弦的距离变化率折射误差修正方法可以实现高精度的折射误差修正，其精度比常规的差分方法高20%，并且具有实际有效性和可操作性.如果要得到真实速度，可以在利用精确位置微分的基础上，再利用考虑经折射误差修正后的真实距离变化率的递推最小二乘估计方法获得.本文方法可以直接应用到单脉冲雷达系统中，以进一步提高其测量精度.本方法的不足是计算较为复杂，这也是下一步研究的课题之一.

［1］刘利生，吴 斌，吴正容，等.外弹道测量精度分析与评定［M］.北京：国防工业出版社，2010.

［2］焦培南，张忠治.雷达环境与电波传播特性［M］.北京：电子工业出版社，2007.

［3］张 瑜，赤 娜，胡笑君.光学雷达大气折射误差修正方法研究［J］.电光与控制，2009，16（5）：16-22.ZHANG Yu，CHI Na，HU Xiaojun.Research on atmospheric refraction error correction method of optic radar［J］.Electronics Optics ＆Control，2009，16（5）：16-22.（in Chinese）

［4］杨志强，陈祥明，赵振维.对流层电波折射误差修正经验模型研究［J］.电波科学学报，2008，23（3）：580-584.YANG Zhiqiang，CHEN Xiangming，ZHAO Zhenwei.Empirical model for radio wave refractive error correction of troposphere［J］.Chinese Journal of Radio Science，2008，23（3）：580-584.（in Chinese）

［5］JIANG C Y，WANG B D.Atmospheric refraction corrections of radio wave propagation for airborne and satellite-borne radars［J］.Science in China：Series E，2001，44（3）：280-290.

［6］张 瑜，赤 娜，侯 佳，等.大气折射引起的雷达定位误差模型［J］.电光与控制，2009，16（7）：65-68.ZHANG Yu，CHI Na，HOU Jia，et al.Model of radar locating error caused by atmosphere refraction［J］.Electronics Optics ＆Control，2009，16（7）：65-68.（in Chinese）

［7］刘宗伟，刘夫体，甘友谊，等.微波辐射计在雷测数据折射误差修正中的应用［J］.电波科学学报，2011，26（6）：1154-1157.LIU Zongwei，LIU Futi，GAN Youyi，et al.Application of microwave radiometer in the refractive error correction of radar measurement data［J］.Chinese Journal of Radio Science，2011，26（6）：1154-1157.（in Chinese）

［8］张 瑜.电磁波空间传播［M］.西安：西安电子科技大学出版社，2007.

［9］张 瑜，胡笑君.雷达方位角折射误差修正方法研究［J］.现代雷达，2008，30（12）：9-11.ZHANG Yu，HU Xiaojun.Study on the method of correction for radar azimuth angle refraction error［J］.Modern Radar，2008，30（12）：9-11.（in Chinese）