基于干扰位置预测的稳健波束形成方法
吴 梦 刘宏伟 周生华 罗 涛 王 旭
(西安电子科技大学 雷达信号处理国家重点实验室,陕西 西安710071)
引 言
自适应波束形成[1]通过调整各阵元的加权值使方向图的主瓣指向目标,同时在干扰方向形成零陷,以达到抑制干扰提高目标信号检测性能的目的.在理想环境下传统自适应波束形成方法[2]可以获得良好性能,但在高速平台雷达的应用中会受到一些实际因素的影响,其性能严重下降.对于高速平台雷达,干扰相对阵列的入射方向可能快速变化,权值训练数据难以反映权值应用时刻的干扰方向[1,3],使得方向图零点与干扰实际方向产生偏差,无法有效抑制干扰,导致阵列输出信干噪比严重下降.当输入信噪比较高时,自适应波束形成方法对指向误差有很大的敏感度[4-8],目标信号会被当作干扰抑制掉,进一步加剧输出信干噪比的损失.如何提高自适应波束形成在高速平台雷达应用中对干扰方向快速变化和指向误差的稳健性,是一个值得研究的问题.
目前,针对指向误差引起的目标信号相消问题,已有一些较好的解决方法.干扰协方差矩阵重构(Interference Covariance Matrix Reconstruction,ICMR)[9]法根据目标方向的先验信息和主瓣宽度确定干扰所在角域,并在该角域对空间谱函数进行积分以重构干扰协方差矩阵,有效滤除了协方差矩阵中的期望信号分量;文献[10]则通过对指向误差的迭代估计修正了干扰所在角域,进一步提高了ICMR算法的稳健性.矩阵加权(Adaptive Matrix Approaches,AMA)[11]方法通过对阵列接收信号进行矩阵加权来综合方向图,不但具有良好的主瓣保形能力,还能在抑制强干扰的同时获得较低旁瓣;文献[12]则是通过约束主瓣增益波动范围,提高了AMA算法对较大指向误差的稳健性.上述方法主要解决了目标信号相消问题,但对方向快速变化的干扰无法有效抑制.为提高雷达对方向快速变化干扰的抑制能力,可通过加宽干扰零陷来实现.常用的零陷加宽方法主要有协方差矩阵锥消(Covariance Matrix Taper,CMT)[13]法和导数约束法[14].CMT算法是用协方差矩阵与空间扩展矩阵的Hadamard乘积代替原始协方差矩阵求解自适应权,无需知道干扰的方向,零陷宽度可以任意设置;导数约束法通过在已知的干扰方向施加导数约束以加宽零陷,其本质是增加干扰邻近方向的增益约束,属于CMT算法的特例[15].而在实际应用中,若是自适应权值更新速度相对太慢[1,3],展宽范围设置不当,上述零陷加宽方法的干扰抑制性能仍会下降.为此我们可以根据干扰方位的变化规律来设置零陷,确保权值应用期间干扰始终处于所设定的零陷范围内.
该文以高速平台雷达为应用背景,提出了一种基于干扰位置预测的稳健波束形成方法,该方法在干扰方向快速变化和指向误差并存的情况下有效减少输出信干噪比的损失.首先建立了干扰信号模型,定义了归一化空间频率并得出其随时间的变化关系.然后利用历史数据估计干扰归一化空间频率及其变化率,继而预测权值应用时期内干扰的归一化空间频率,给出零陷范围.最后,通过矩阵加权的方式对零陷范围进行低增益约束以抑制干扰,同时约束主瓣区域响应不衰减以提高波束形成对指向误差的稳健性.仿真实验表明,所提方法可以有效抑制方向快速变化的干扰信号,并对指向误差具有较好的稳健性,有效延长了权值使用时间.
1 信号模型
考虑一个由M元各向同性阵元组成的阵列和一个窄带干扰源,如图1所示,o点为阵列的参考点,干扰源Q到o点的向量记为ro,干扰源到第i(i=1,…,M)个阵元Ai构成向量ri,o点到阵元Ai的向量为pi.
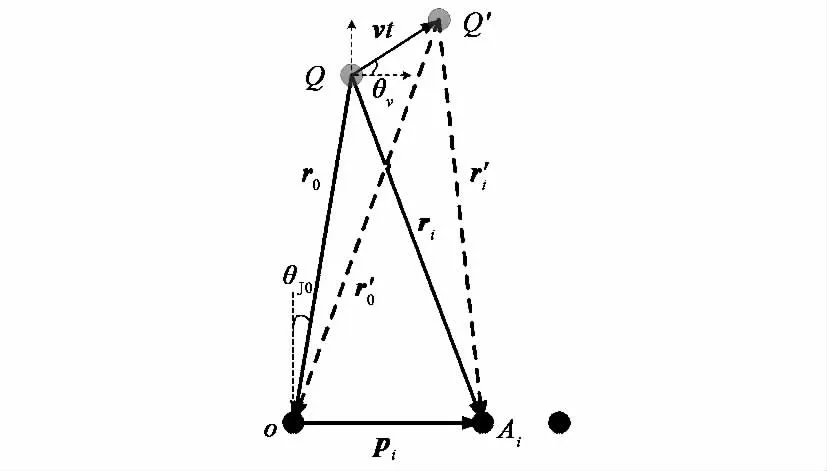
图1 空间示意图
从图中可以看出ri=ro+pi,那么Q点到阵元Ai的距离与到o点的距离差为
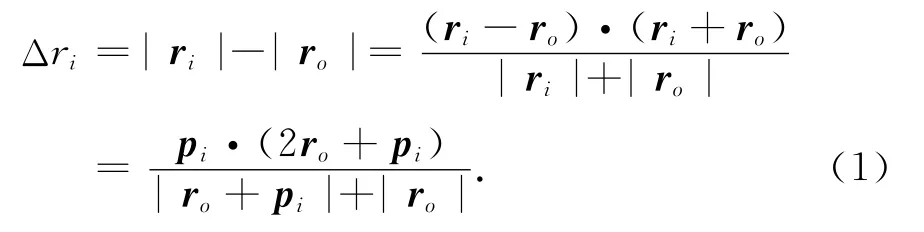
式中,符号·表示两向量的内积.当雷达的工作波长为λ时,由距离差Δri引起的相位差可以表示为φi=2πΔri/λ.将式(1)代入φi,并对其分子分母同除以|ro|有
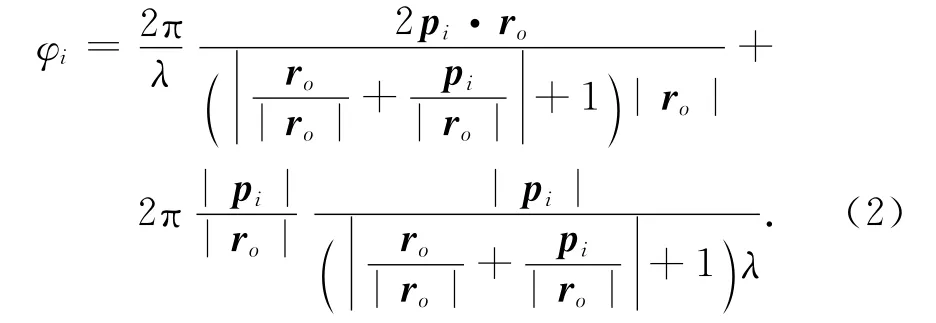
在干扰源位于阵列远场时,干扰到阵列参考点的距离远大于阵列孔径,有|ro|≫|pi|,那么,式(2)可以近似为
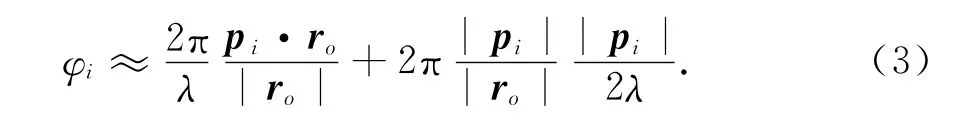
一般情况下|pi|与波长λ是一个数量级的,那么式(3)中的第二项可以忽略不计,进一步近似得到

若阵列平台运动速度为vA,干扰源运动速度为vJ,此时干扰源相对于阵列平台的运动速度为v=vJ-vA.不失一般性,假设干扰源在Q点的时刻为初始时刻.那么t时刻,干扰源运动了距离vt到Q′点,干扰源到阵列参考点的向量变为r′o,如图1所示,则有=ro-vt,干扰信号到第i个阵元与到阵列参考点之间的相位差可以表示为
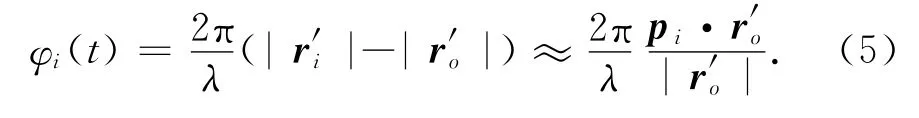
假设短时间内干扰运动距离远小于干扰源到阵列的距离,即|vt|≪|ro|,那么相位差式(5)可以进一步近似为

从式(6)可以看出,该相位差由两部分构成,固定相位差和运动引起的相位差.那么干扰信号到达各阵元的相位差所组成的向量为a=[1,ejφ2(t),…,ejφM(t)]T,可称为干扰信号的导向矢量.
从空域滤波的角度来看,天线方向图相当于一个空域滤波器.为表征信号的空域特征,定义归一化空间频率为
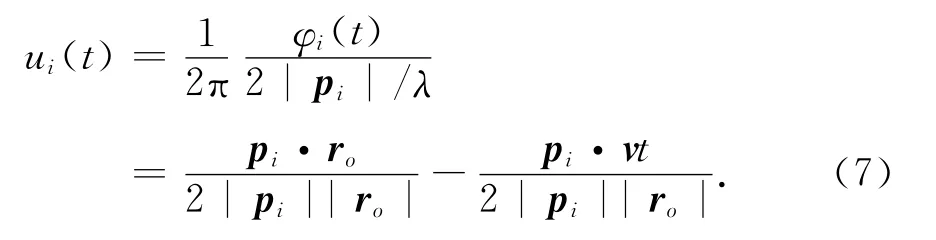
由以上讨论可以得出,在短时间内干扰运动距离远小于干扰源到阵列距离的条件下,干扰源的归一化空间频率是随时间近似线性变化的.
上述分析适用于任意结构阵列,下面以半波间距的均匀线阵为例描述干扰的信号模型,如图1所示,θJ0为干扰的初始方向,ro=|ro|为干扰到阵列的初始距离,v为干扰相对阵列平台的运动速度v的大小,θv为运动速度与阵列方向的夹角.根据式(7)得到第n个采样时刻干扰源的归一化空间频率,可以表示为
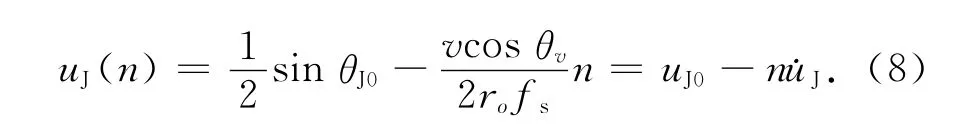

式中,fr为脉冲重复频率.假设干扰源的归一化空间频率在L个脉冲重复周期内服从线性变化,那么第l(l=1,…,L)个脉冲时刻干扰源的归一化空间频率为uJ(l)=uJ0-lΔuJ.
考虑雷达观测区域内存在K个与目标信号不相关的干扰信号,为获得独立同分布的样本,对一个脉冲重复周期内的阵列接收信号进行采样.当训练数据中含有目标回波信号时,单个脉冲时刻的接收数据可以表示为
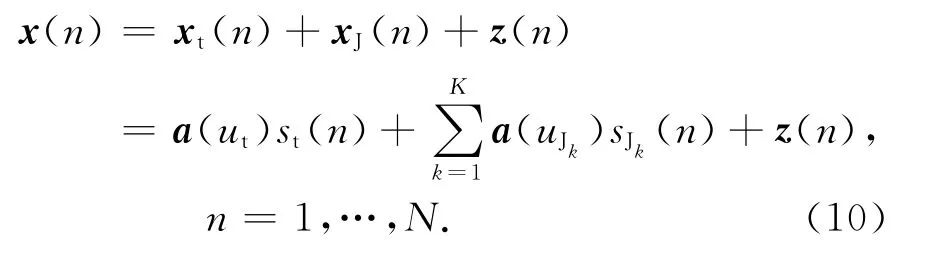
式中:a(ut)为目标在归一化空间频率ut时的导向矢 量,表 示 为a(ut)=[1,ej2πut,…,ej2π(M-1)ut]T;st(n)为目标回波幅度;a(uJk)为第k个干扰在归一化空间频率uJk时的导向矢量,表示为a(uJk)=[1,ej2πuJk,…,ej2π(M-1)uJk]T;sJk(n)为第k个干扰信号的幅度;z(n)为噪声矢量;N为接收信号的快拍数.
由于目标信号与干扰信号、噪声互不相关,接收数据的协方差矩阵可以表示为

式中:符号E[·]表示求数学期望;Rt=E[xt(n)为目标协方差矩阵E[|st(n)|2]为 目标回波功率;RJ+z=E[(xJ(n)+I为干扰噪声协方差矩阵为第k个干扰的信号功率为噪声功率.
通常自适应方向图的零陷比较陡峭,尤其是在阵列尺寸较大的情况下,干扰方向的轻微变化都能导致干扰抑制性能的大幅下降.为有效抑制方向快速变化的干扰,可以根据上述结论预测权值应用时期干扰的归一化空间频率,给出对应的零陷范围,确保干扰始终处于方向图的零陷内.
2 稳健的自适应波束形成方法
根据上一节分析得出,对于高速平台雷达,干扰的归一化空间频率是脉间变化的.这会导致权值训练数据所得方向图零点与权值应用时刻的干扰位置产生偏差[1],使得干扰不能被有效抑制.同时在实际应用中,当权值训练数据包含目标回波信号时,较小的指向误差都会引起目标信号相消现象[4-8].针对以上问题并存的情况,下面给出一种基于干扰位置预测的稳健波束形成方法.该方法首先利用已估计的干扰归一化空间频率及其变化率预测出权值应用时刻的归一化空间频率,再采用矩阵加权的方式对预测的干扰区域进行低增益约束,达到抑制干扰的目的.同时对主瓣增益和旁瓣电平进行约束,可以防止主瓣分裂并压低旁瓣.
利用权矩阵W=[w1,w2,…,wQ]∈CM×Q对阵列接收信号(10)进行加权,阵列输出的信干噪比RSIN可以表示为
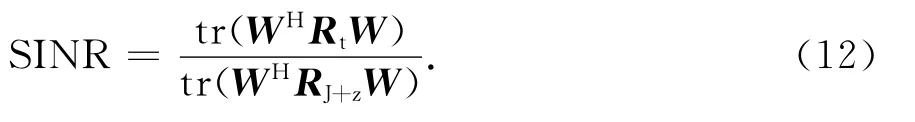
式中,符号tr(·)表示求矩阵的迹.利用性质tr(AB)=tr(BA),令T=WWH,式(12)可以变为

根据最大化阵列输出信干噪比准则可以求得最优自适应权值,等价为如下带约束的优化问题:
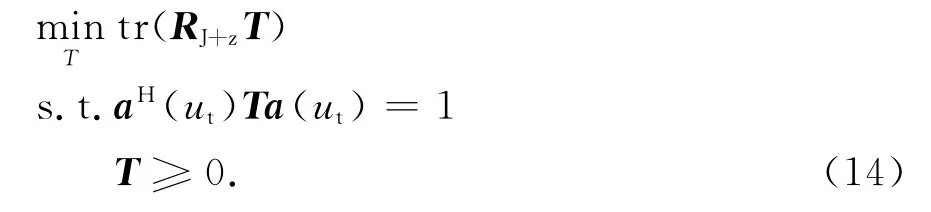
实际中,理想的RJ+z一般无法获得,而是用接收数据的协方差矩阵R的有限次快拍估计=来代替.
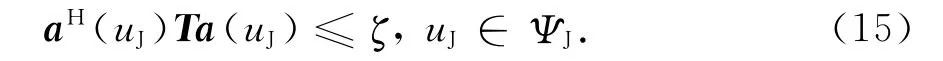
式中,ζ为干扰区域增益的上界.
为防止指向误差引起的主瓣分裂和抖动,文献[12]增加了对主瓣区域Ψm增益的约束为
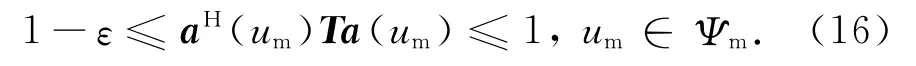
式中:ε为主瓣增益的最大波动范围,定义为ε=1-10-εdB/10,εdB为主瓣区域波动的最大值.同时为防止旁瓣增益的抬高,对旁瓣区域Ψs增益进行约束
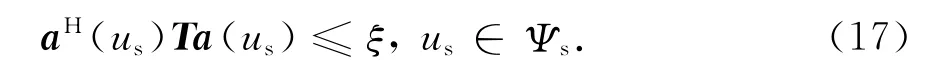
式中,ξ为旁瓣区域增益的上界.
综上所述,为提高自适应波束形成在高速平台雷达应用中对指向误差和干扰方向快速变化的稳健性,给出如下优化模型为
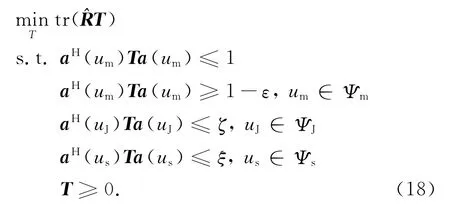
从上式可以看出,目标函数和约束方程均是关于T的线性函数,式(18)是一个半正定规划问题,可以应用凸优化工具包CVX[16]求得全局最优解,再利用特征值分解法[12]得到最小维数的权矩阵W.
3 仿真实验
通过仿真实验验证所提方法的有效性.仿真条件:假设雷达天线阵列为半波间距的等距线阵,阵元数M=20,脉冲重复频率fr=500Hz.空间存在三个独立的干扰源,初始归一化空间频率分别为{-0.3,0.25,0.4},其脉间变化率分别为{ΔuJk={5.1×10-4,-3.4×10-4,-4.1×10-4},干噪比分别为40dB、30dB和30dB.阵列接收数据中含有目标回波信号,目标信号的归一化空间频率为ut=0.03,期望方向对应的空间频率为0,即主瓣存在0.03的指向误差.接收机噪声为零均值的高斯白噪声.将所提方法和Capon算法[2],CMT算法[13]及ICMR算法[10]进行比较.实验中,CMT算法[13]为提高算法的稳健性将对角加载技术和零陷展宽相结合,加载量为10σ2z,零陷宽度为0.06;ICMR算法[10]的主瓣宽度为0.06;所提方法的主瓣区域为Ψm=[-0.03,0.03],主瓣区域增益波动的最大值εdB=0.5dB,旁瓣区域为Ψs=[-0.5,-0.1]∪[0.1,0.5],其中符号∪表示两个区间的并集,旁瓣电平为ξ=-30dB,权值适用时间为60个脉冲重复周期,干扰区域为ΔuJk,uJk0],干扰区域的增益不能大于ζ=-60dB.
3.1 方向图对比
在信噪比为10dB、快怕数为100的条件下将所提方法与另外三种算法形成的方向图进行比较,结果如图2所示.图2中旁瓣区域的竖实线表示初始脉冲时刻干扰的归一化空间频率,竖虚线表示第60个脉冲时刻干扰的归一化空间频率.从图2可以看出:当主瓣存在0.03(相当于3.4°)的指向误差时,Capon算法和CMT算法都出现了严重的目标信号相消现象;ICMR算法虽在一定程度上缓解了信号相消问题,但对较大指向误差的稳健性较弱,主瓣响应仍然会产生畸变.在干扰抑制方面,Capon算法和ICMR算法只能在干扰的初始位置处形成尖锐的零陷,CMT算法对此零陷有所展宽,但展宽范围只在干扰初始位置的周围,并不能包含干扰实际的变化范围.所提方法不但能对主瓣进行保形,还能保证干扰始终处于零陷范围内.这正是利用了干扰归一化空间频率的变化性质给出对应的零陷范围,从而有效应对干扰方向的快速变化.
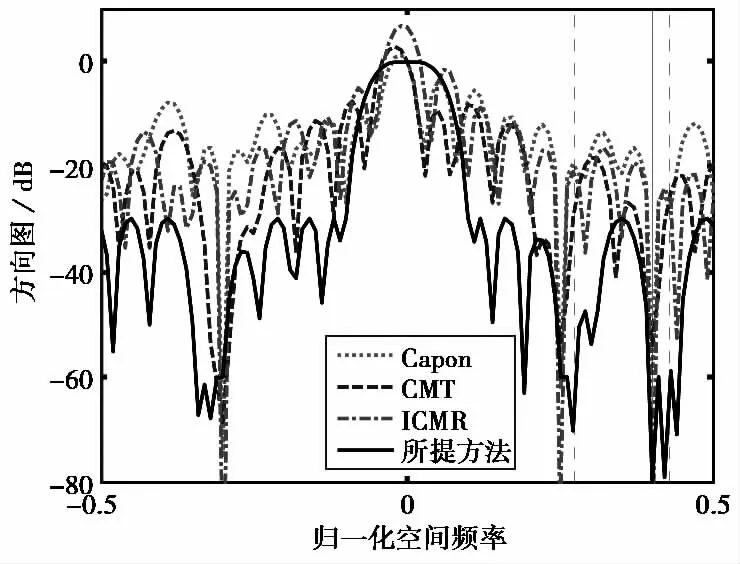
图2 方向图对比
3.2 输出信干噪比与输入信噪比的关系
在权值不同应用时刻,观察各算法的输出信干噪比随输入信噪比的变化.仿真结果是在快怕数为100的条件下进行100次蒙特卡洛实验平均所得.从图3可以看出:初始脉冲时刻干扰的归一化空间频率未变化时,四种算法在低信噪比情况下的性能相当;但随着输入信噪比的提高,Capon算法和CMT算法的性能逐渐下降,ICMR算法和所提方法仍能保持较好的性能.由于ICMR算法对较大指向误差的稳健性弱于所提方法,故随着信噪比的增加其输出信干噪比要低于所提方法.图4为权值应用的第60个脉冲时刻各算法的性能比较图,可以看出Capon算法、CMT算法、及ICMR算法的输出信干噪比远低于所提方法.因为此时干扰的归一化空间频率发生变化,权值训练数据所得方向图零点与权值应用时刻的干扰位置产生偏差,干扰已移出方向图的零陷.虽然CMT算法对零陷有所展宽,但展宽范围已不足以应对干扰的变化.
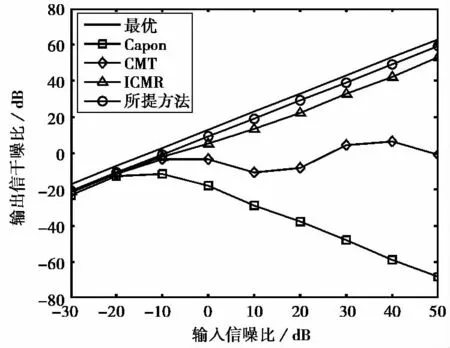
图3 初始脉冲时刻
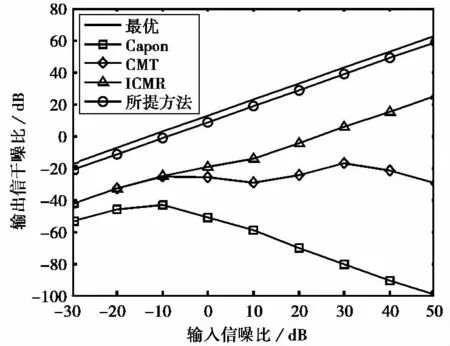
图4 第60个脉冲时刻
3.3 输出信干噪比随时间的性能
图5给出了信噪比为10dB、快怕数为100的条件下各算法输出信干噪比随时间的变化,仿真结果由100次蒙特卡洛实验平均所得.从图中可以看出,Capon算法、CMT算法和ICMR算法对主瓣指向误差的稳健性较差,故在初始脉冲时刻的输出信干噪比就低于所提方法.由于干扰的归一化空间频率随时间变化,权值训练数据形成的零点位置和干扰的实际位置发生偏差,Capon算法和ICMR算法的性能随着时间的推移急剧下降.CMT算法的输出信干噪比虽能在较短时间内保持平稳,但相比所提方法的权值适用时间较短.
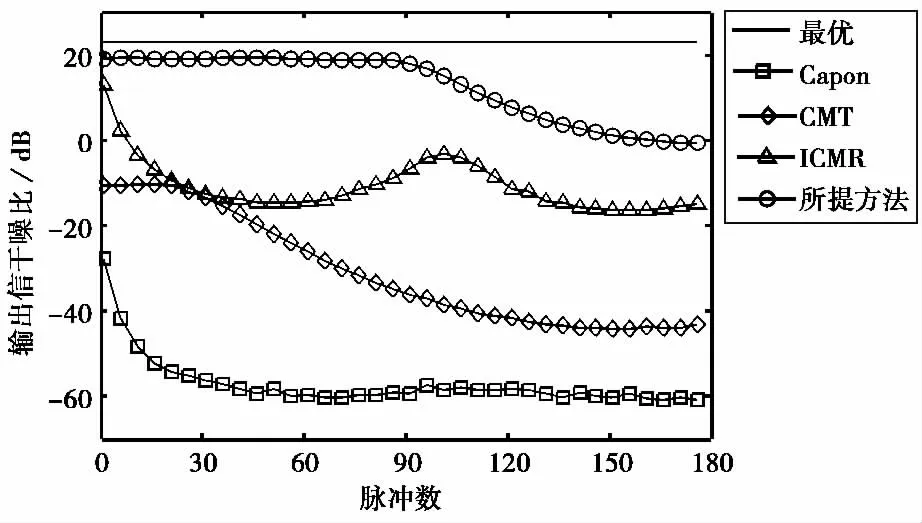
图5 输出信干噪比随时间的变化
4 结 论
针对高速平台雷达阵列进行自适应波束形成时性能下降的问题,该文给出了一种基于干扰位置预测的稳健波束形成方法.该方法利用干扰归一化空间频率在短时间内随着近似线性变化的特性,预测出权值应用时期的干扰区域,再通过矩阵加权的方式对干扰区域进行低增益约束以抑制干扰,同时约束主瓣区域响应一定以防止目标信号输出功率的损失.仿真实验结果表明,所提方法可以有效提高输出信干噪比,延长权值的使用时间,相比已有波束形成方法更能有效地抑制方向快速变化的干扰信号,对较大指向误差更具稳健性.所提方法的权值计算采用了凸规划算法,该算法能够获得优化问题的全局最优解,只是在一些雷达系统中该算法应用范围遭到限制,因此下一步一个有意义的研究问题是如何采用更高效的算法解决该文的优化问题.
[1]王永良,丁前军,李荣峰.自适应阵列处理[M].北京:清华大学出版社,2009.
[2]CAPON J.High-resolution frequency-wavenumber spectrum analysis[J].Proceeding of the IEEE,1969,57(8):1408-1418.
[3]RIBA J,GOLDBERG J,V`AZQUEZ G.Robust beamforming for interference rejection in mobile communications[J].IEEE Transactions on Signal Processing,1997,45(1):271-275.
[4]RUBSAMEN M,PESAVENTO M.Maximally robust capon beamformer[J].IEEE Transactions on Signal Processing,2013,61(8):2030-2041.
[5]许京伟,廖桂生,朱圣棋.基于幅相线性约束的自适应和差波束形成方法研究[J].电子学报,2013,41(9):1724-1729.XU Jingwei,LIAO Guisheng,ZHU Shengqi.Approach of adaptive sum and difference beamforming based on magnitude and phase linear constraint[J].Acta Electronica Sinica,2013,41(9):1724-1729.(in Chinese)
[6]LI J,WEI G,DING Y.Adaptive beamforming based on covariance Matrix reconstruction by exploiting interferences’cyclostationarity[J].Signal Processing,2013,93(9):2543-2547.
[7]王 勇,刘宏伟,纠 博,等.特定角域低增益的稳健方向图综合算法[J].电波科学学报,2012,27(4):812-818.WANG Yong,LIU Hongwei,JIU Bo,et al.Robust beampattern synthesis algorithm with low response in a specified region[J].Chinese Journal of Radio Science,2012,27(4):812-818.(in Chinese)
[8]李洪涛,贺亚鹏,朱晓华,等.基于谱分析的稳健自适应波束形成算法[J].电波科学学报,2012,27(1):147-151.LI Hongtao,HE Yapeng,ZHU Xiaohua,et al.Spectral analysis based robust adaptive beamforming algorithm[J].Chinese Journal of Radio Science,2012,27(1):147-151.(in Chinese)
[9]GU Y,LESHEM A.Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J].IEEE Transactions on Signal Processing,2012,60(7):3881-3885.
[10]LU Z,LI Y,GAO,et al.Interference covariance Matrix reconstruction via steering vectors estimation for robust adaptive beamforming[J].Electronics Letters,2013,49(22):1373-1374.
[11]LI J,XIE Y,STOICA P,et al.Beampattern synthesis via a matrix approach for signal power estimation[J].IEEE Transactions on Signal Processing,2007,55(12):5643-5657.
[12]罗 涛,刘宏伟,纠 博,等.基于矩阵加权的稳健波束形成方法[J].电波科学学报,2014,29(1):135-142.LUO Tao,LIU Hongwei,JIU Bo,et al.Robust beamforming via Matrix weighted method[J].Chinese Journal of Radio Science,2014,29(1):135-142.(in Chinese)
[13]GUERCI J R.Theory and application of covariance matrix tapers for robust adaptive beamforming[J].IEEE Transactions on Signal Processing,1999,47(4):977-985.
[14]ERSHMAN A B,NICKEL U,BOHME J F.Adaptive beamforming algorithms with robustness against jammer motion[J].IEEE Transactions on Signal Processing,1997,45(7):1878-1885.
[15]ZATMAN M.Comments on“theory and application of covariance matrix tapers for robust adaptive beamforming”[J].IEEE Transactions on Signal Processing,2000,48(6):1796-1800.
[16]GRANT M,BOYD S.CVX:Matlab software for disciplined convex programming,version 2.0beta[EB/OL].[2014-07-01]http://cvxr.com/cvx.September,2013.

