新型煤气柜内压弯曲分析方法研究

李正良，于 伟，胡 浩，刘欣鹏，王凌西

(1.重庆大学 土木工程学院，重庆 400045；2.山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400045)

新型煤气柜内压弯曲分析方法研究

李正良1,2†，于 伟1†，胡 浩1，刘欣鹏1，王凌西1

(1.重庆大学 土木工程学院，重庆 400045；2.山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400045)

严格控制新型高压煤气柜内压弯曲，是保证结构气密性和正常运行的关键问题，其受力模型为具有多根环向加筋圆柱壳受局部内压作用的弹性弯曲.把弹性地基板条梁法拓展应用到该结构体系；同时对传统离散加筋法进行改进，考虑了壳体厚度、半径及加筋肋间距对结构环向刚度的影响.以30万m3新型煤气柜为例，采用弹性地基板条梁法、改进离散加筋法、密加筋法和有限元法进行了分析.在此基础上，给出了判定环向加筋圆柱壳密肋、稀肋的方法.分析结果表明，弹性地基板条梁法具有适用性强、精度高、效率好；当环向加筋间距dr>3.875 (Rh)1/2时，改进离散加筋法计算效率较高.

薄壁结构；气柜；弹性地基板条梁法；改进离散加筋法；影响宽度

干式煤气柜是一种可以储存可燃气体、节约能源和保护环境的大型、特种结构，广泛用于冶金、石化、市政等行业.新型(圆形)干式煤气柜具有密封性能好、储气压力大、活塞运行自稳性好和煤气死空间容积小等优点[1].因该新型煤气柜相应的设计理论研究不足，无专用设计规程，所以迫切需要对其结构的计算理论和方法等进行全面深入的研究，提出合理的分析理论和计算方法，为实际工程的应用和设计规程的编制提供参考.

20世纪70年代，上海宝钢一期工程中从日本引进3台干式煤气柜.为弥补干式煤气柜的设计计算理论和方法，国内学者做了不少研究，并取得了显著成果.姜德进[2-3]基于简化力学模型进行了正多边形干式煤气柜走道平台、立柱和柜体侧板的内力分析；游理华[4]对曼型干式煤气柜柜体计算理论和方法及板的弹性弯曲和后屈曲进行了研究；童根树等[5]对MAN型干式气柜的力学模型、自振特性和地震响应进行分析；周伟[6]采用有限元对新型煤气柜柜体的强度和柜顶的稳定进行仿真分析；但堂波[7]对大型正多边形(M.A.N)干式煤气柜结构构件在内压和风荷载作用下的受力性能进行理论分析和有限元验证；贾冬云等[8-9]采用理论分析和试验研究相结合的方法，对大型正多边形煤气柜立柱和加肋壁板进行了系统的研究.

目前就新型煤气柜高压煤气作用的整体弹性弯曲研究鲜有涉及.本文首先建立合理简化分析模型，其次改进传统离散加筋法和拓展弹性地基板条梁法，最后，通过与传统方法和有限元结果进行对比，给出判定环向加筋圆柱壳密、疏的建议公式，并提出适合工程应用的分析方法，供理论研究和工程设计参考.

1 空间壳体分析法

1.1 新型煤气柜煤气压力作用下的简化力学模型

新型煤气柜主要由加劲壳体系的浅球壳柜顶、外部纵横加筋的圆筒形柜体及穹形拱状周边设有箱形环梁的活塞构成[1]，如图1所示.柜体纵向加筋肋(立柱)主要承受柜顶、柜体重量及风和地震作用产生的竖向力，环向加筋肋和壳体主要承受内部气体压力和其他外荷载的水平力，且回廊属于附属结构[1，10].煤气柜正常运行时，柜体承受内部高压气体作用，根据其结构受力特点，研究柜体局部内压时可仅考虑柜体壳体及环向加筋肋，如图2所示.

考虑柜体内局部高度受均布内压q(x)，坐标系如2图所示.将q(x)沿壳母线方向展成富氏级数[11]：

(1)

式中:q0为均布压力；S0=H/l；Sn=2sin(nπH/l) / (nπ).

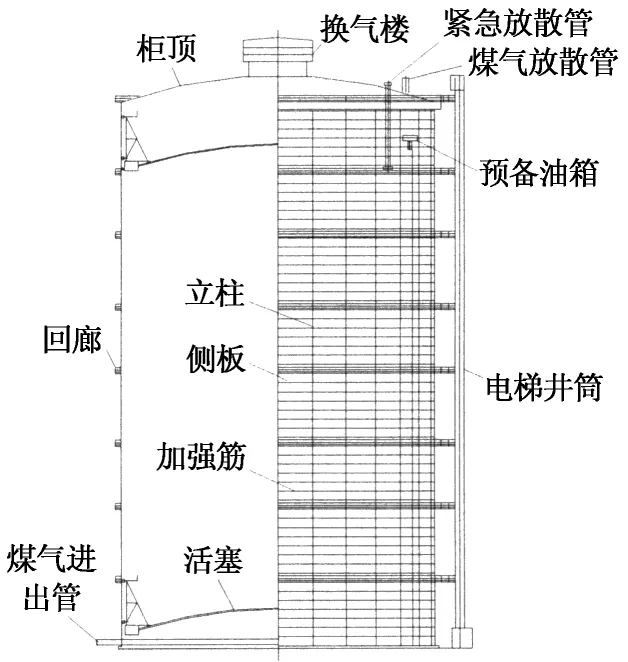
图1 新型干式煤气柜

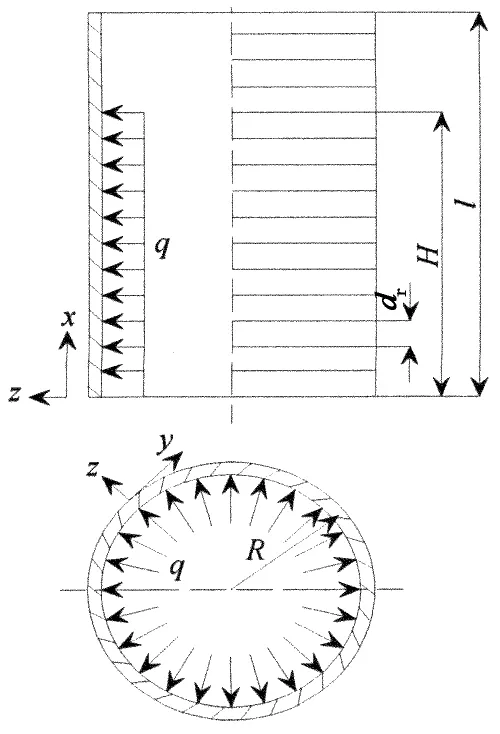
图2 环向加筋圆柱壳

1.2 密加筋方法

基本假定除服从乐甫-基尔霍夫假设外还需做如下假设：1) 采用Donnell扁壳方程；2) 加筋肋等间距足够密布置，不计加筋肋宽度[12-13].

根据文献[14-15]，仅受法向局部内压作用的环向加筋圆柱壳等效为构造上的正交各向异性圆柱壳,其关于位移的微分方程：

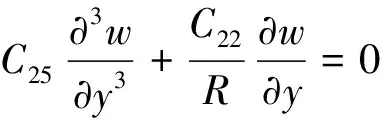
(2)

式中：u，v，w分别为x,y,z方向的位移；Cij为结构弹性常数，具体可参看文献[14-15].

壳体中面应力与位移的关系采用基于文献[16]的关系式：

(3)

式中：E为弹性模量；μ为泊松比；G为剪切模量.

引入函数F(x)，使

u=δ1F；v=δ2F；w=δ3F．

(4)

其中δ1，δ2，δ3参考文献[15].

则式(2)简化为：

(5)

式中：

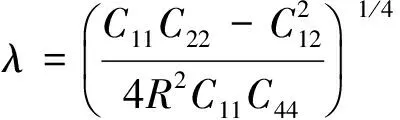
因新型干式煤气柜属长壳，根据圣维南原理，结构底部自平衡力系产生的影响是局部的[17-18]，且当柜底铰接时，式(5)的全解为：

(6)

根据式(6)并结合式(4)和式(3)可给出加筋圆柱壳的径向位移和应力.

1.3 改进离散加筋方法

传统离散加筋法认为加筋对壳体提供的环刚度集中在筋与蒙皮的连接突缘宽度范围内[19].而改进离散加筋法，引入的δ序列内含一待定影响宽度参数，该参数考虑了壳体厚度、半径及加筋肋间距的影响.

基本假定[12-13,19]：1) 壳的横向剪切刚度为无限大；2) 考虑加筋的偏心作用；3) 加筋与壳体在径向和筋条方向位移连续；4) 不考虑加筋的侧向弯曲刚度；5) 环向加筋等距分布；6) 加筋布置稀疏；7) 不考虑两相邻加筋间的相互影响.

环向离散加筋圆柱壳仅受局部内压作用的平衡微分方程为：

(7)

采用基于文献[16]的环向加筋的应力关系式：

(8)

式中:e2=Sr/Ar;e2，Sr，Ar分别为环向加筋对壳体中面的偏心距，静矩和环向加筋截面积.

考虑加筋对连接壳体环刚度的实际影响，引入含一待定参数服从正态密度分布函数类型的δ序列，则改进的环向等间距离散分布的加筋圆柱壳的内力表达式为：

(9)

式中：εx0,εy0,γxy0为壳体中面应变；br1为加筋对壳体的影响宽度；N2为环向加筋个数；h为壳体厚度；Ir，Jr分别为环向加筋对壳体中面的惯性距和扭矩；B=Eh/(1-μ2)；D=Eh3/12(1-μ2).

δ序列所含待定参数br1，由有限元参数化分析确定.分析了壳体半径、厚度、加筋肋间距、T型加筋肋翼缘宽度、厚度和腹板高度对加筋肋连接壳体的影响宽度规律.采用无量纲化数据拟合得环向加筋对壳体的影响宽度公式(10).结构参数和分析结果分别如表1和表2所示.

表1 结构参数

表2 环向加筋不同间距及加筋影响宽度

(10)

环向加筋圆柱壳上下端简支时，位移函数：

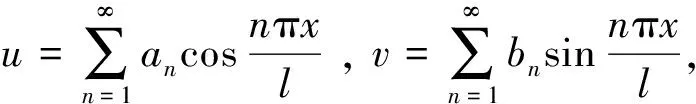
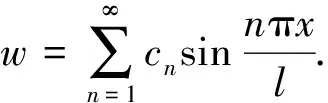
(11)

式(11)满足x=0,l两端的简支条件：

w=v=Nx=Mx=0.

(12)

利用广义伽辽金法[14]，结合式(7),式(9)和式(10)给出结构的伽辽金积分格式：

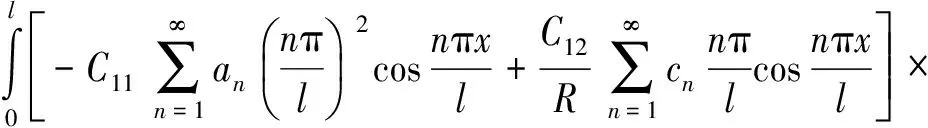
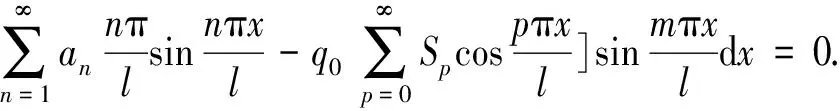
(13)

采用有限项逼近，求解式(13)可得系数an,bn,cn.再结合式(3)和式(8)得结构径向位移和应力.

2 弹性地基板条梁法

新型煤气柜在煤气压力作用下，将受到壳体的环向弹性约束和环向加筋的径向弹性约束.因此，该结构可简化为具有弹性支撑和弹性地基的连续板条梁，当环向加筋较密(N2>5)时可简化为单跨弹性地基板条梁.

圆柱壳提供的基床系数[20]K1=Eh/R2，板条梁的柱形弯曲刚度D=Eh3/12(1-μ2).根据柔度法推导单个环向加筋的弹性系数.环向加筋的环向力T=PR，在T作用下，环向加筋的总伸长：

(14)

式中:P为均布内压力；R为环向加筋的半径.

半径与圆周长度的比例1∶2π，则半径伸长：

(15)

当ΔR=1时，所需施加的压力P=EAr/R2，即单个环向加筋的弹性系数ki=EAr/R2.单个环向加筋在间距dr宽度上的平均刚度为K2=EAr/R2dr.

2.1 具有弹性支撑和弹性地基的连续板条梁法

分析新型煤气柜在煤气压力作用下的轴对称弯曲时,环向加筋对圆柱壳的约束可简化为弹性支撑.具有弹性支撑和弹性地基的连续板条梁如图3所示．

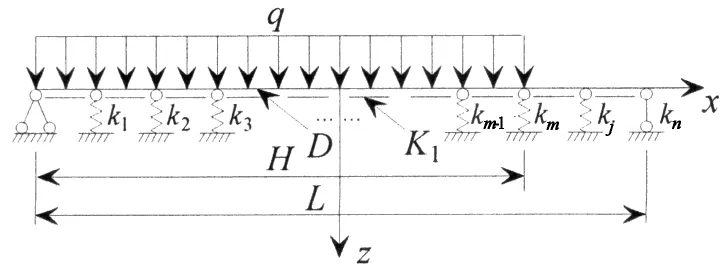
图3 具有弹性支撑和弹性地基的连续板条梁

通过定义由理论推导的弹性系数ki，K1，采用beam44和combin14单元建立有限元模型，对具有弹性支撑和弹性地基的连续板条梁进行分析.

环向加筋圆柱壳的环向应力为：

σ2=Ew/R．

(16)

2.2 单跨弹性地基板条梁法

局部均布荷载q可采用式(1)进行计算，弹性地基板条梁的弯曲微分方程为：

(17)

式中：k=K1+K2.

当弹性地基梁较长时，其右端位移为有限值；当x=0时，w=w"=0，则式(17)的全解为：

(18)

式中：λ=(k/4D)1/4.环向加筋圆柱壳的环向应力采用式(16)进行计算.单跨弹性地基板条梁如图4所示．

图4 单跨弹性地基板条梁

3 结果对比与讨论

30万m3新型煤气柜，柜体半径R=32.3 m，长度l=108 m，h=7 mm，环向筋采用T型钢(TM122×175)，E=2.06×105MPa，μ=0.3，煤气压力q=15 kPa，充气高度H=93.6 m.

在高性能计算机上采用大型通用有限元程序ANSYS 14.5，对大型环向T型加筋圆柱壳采用shell 181单元建模进行分析.有限元模型如图5所示．

图5 有限元模型

3.1 传统、改进离散加筋法与有限元结果对比

图6 为传统、改进离散加筋法与有限元结果对比.由图6可知，对于两加筋肋中间部分的径向位移，传统和改进离散加筋法结果均与有限元结果比较吻合；加筋肋处的径向位移，传统离散加筋法与有限元结果相对误差达-80.91%～-79.71%，而改进离散加筋法与有限元结果相对误差仅为-19.63%～-6.46%.因此，改进离散加筋法更适合分析大型环向加筋圆柱壳.

1,2,3-两加筋肋中间处的径向位移4,5,6-加筋肋的径向位移

3.2 密、改进离散加筋法与有限元结果对比

环向加筋间距dr分别取0.9，1.2，1.5，1.8，2.4，3.6和7.2 m多种工况.本文仅给出间距分别为dr=1.8和7.2 m的结果.图7为密加筋、改进离散加筋法与有限元结果对比图(dr=1.8 m).由图7(a)可知，3种方法计算所得径向位移整体规律基本吻合.内压作用高度范围内，密加筋计算结果呈直线，改进离散加筋计算结果和有限元计算结果呈有规律波动；仅在结构底部和内压上边界附近径向位移出现突变，原因是结构底部强约束和内压上边界荷载突变，使该两部分壳体处于有矩应力状态.由图7(b)可看出，2种方法所得加筋肋周向应力整体变化规律较吻合，内压作用范围内，有限元计算结果基本呈直线，改进离散加筋法计算结果呈微小波动；密加筋法无法给出加筋肋环向应力，是因其采用了构造的正交各向异性圆柱壳理论.图7(c)和图7(d)分别给出了截断柜体的径向位移和周向应力结果，其中，改进离散加筋法和有限元结果在两加筋肋中间比较接近，但在加筋肋处相差稍大.

图8 为密加筋、改进离散加筋法与有限元结果对比图(dr=7.2 m).由图8(a)可知，改进离散加筋法与有限元计算结果吻合较好，内压作用高度范围内，密加筋法计算结果呈直线.由图8(b)，(c)和(d)可看出，改进离散加筋法与有限元计算结果比较吻合.

参数化分析表明，随着加筋间距的增加，密加筋法结果逐渐偏离有限元结果，而改进离散加筋法结果更接近有限元结果；当大型环向加筋圆柱壳肋间距dr>3.875 (Rh)1/2时，改进离散加筋法计算效率较高.

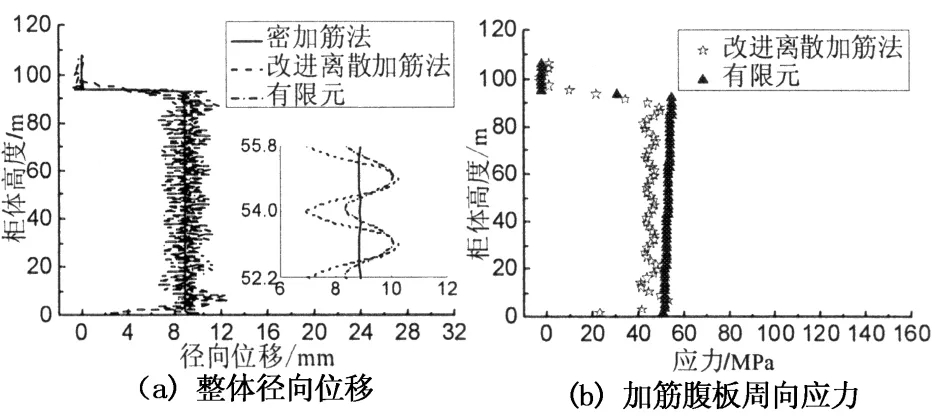
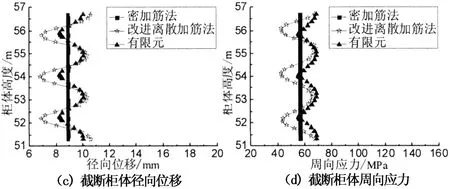
图7 密加筋、改进离散加筋法与有限元结果对比(dr=1.8 m)

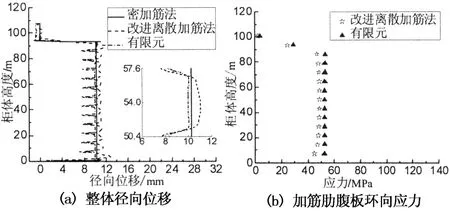
图8 密加筋、改进离散加筋法与有限元结果对比(dr =7.2 m)

3.3 弹性地基板条梁法与加筋圆柱壳的有限元结果对比

跨度或间距dr分别取0.9，1.2，1.5，1.8，2.4，3.6和7.2 m多种工况.本文仅给出间距分别为0.9，1.2，1.8和7.2 m的结果.

图9为弹性地基板条梁与有限元结果对比图(dr=0.9 m).由图9(a)可看出，3种方法计算所得径向位移整体规律比较吻合.局部均布荷载作用长度范围内，单跨弹性地基板条梁法结果呈直线，同加筋圆柱壳的有限元结果比较吻合.此时结构具有环向密加筋的特性.图9(b)和图9(c)可看出，单跨弹性地基板条梁结果约为加筋圆柱壳有限元结果的80%.

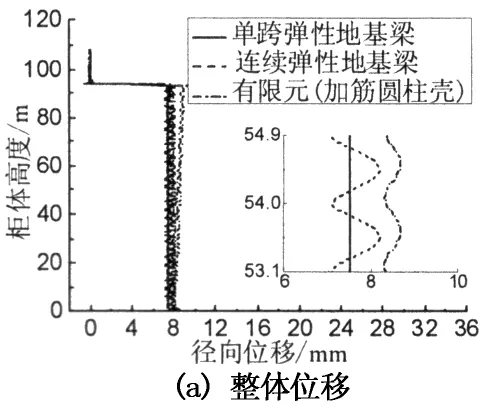
图9 弹性地基板条梁与有限元结果对比(dr=0.9 m)

图10为弹性地基板条梁与有限元结果对比图(dr=1.2 m).由图10(a)可知，3种方法计算所得径向位移整体规律较吻合；局部均布荷载作用长度范围内，与图9(a)相比连续弹性地基板条梁法和有限元结果波动均增大.图10(b)和(c) 与图9(b)和(c)相比可知，随筋间距的增大，连续地基板条梁和有限元结果波动增大.连续弹性地基板条梁与有限元结果规律比较相似，可认为dr=1.2 m的环向加筋圆柱壳处于密肋和稀肋分界.

图11为弹性地基板条梁与有限元结果对比图(dr=1.8 m).由图11(a)可知，3种方法计算所得径向位移结果整体规律基本吻合.局部均布荷载作用长度范围内，单跨弹性地基板条梁结果呈直线，连续弹性地基板条梁和有限元结果均呈有规律较大波动.由图11(b)和(c)可看出，连续地基板条梁结果与有限元结果规律较吻合.图11(c)中，在弹性支撑处周向应力相差稍大，主要是由于具有弹性支撑和弹性地基的连续板条梁中弹性支撑的弹性系数作用位置比较集中.整体和截断结果表明，结构明显具有环向稀肋圆柱壳的特性.

图12为弹性地基板条梁与有限元结果对比图(dr=7.2 m).由图12(a)可知，连续地基板条梁结果和有限元结果均呈有规律较大波动、且规律吻合较好.由图12(b)和(c)可知，连续地基板条梁与有限元结果规律吻合较好，只有在弹性支撑(或加筋肋)处相差稍大.

3.4 两类方法与有限元结果对比

图13为密加筋、单跨弹性地基梁与有限元结果对比图.由图13可知，密加筋法与单跨弹性地基梁法结果相同，有限元结果呈小范围波动.

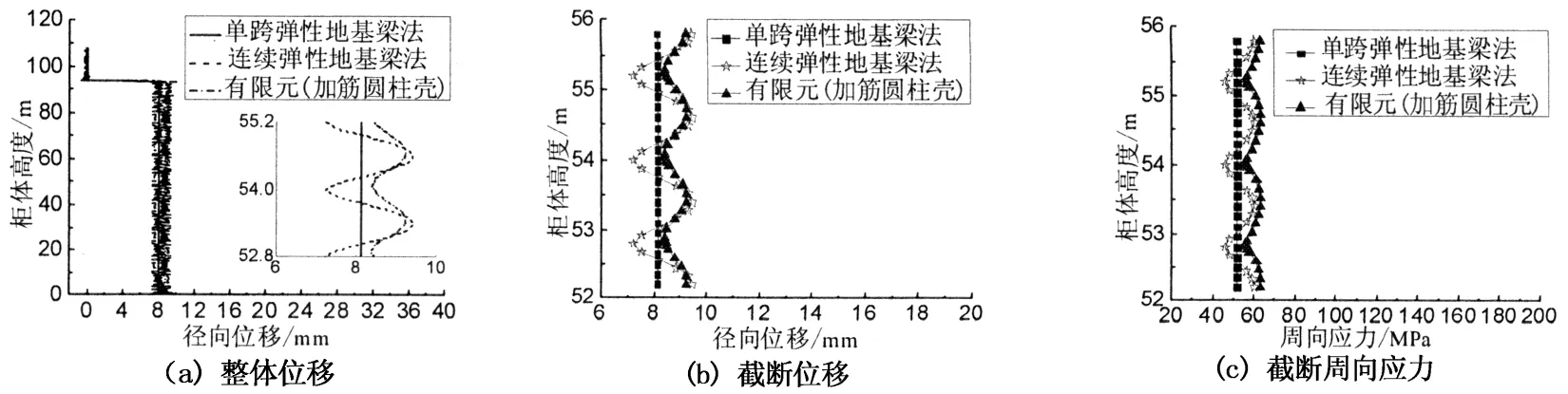
图10 弹性地基板条梁与有限元结果对比(dr =1.2 m)

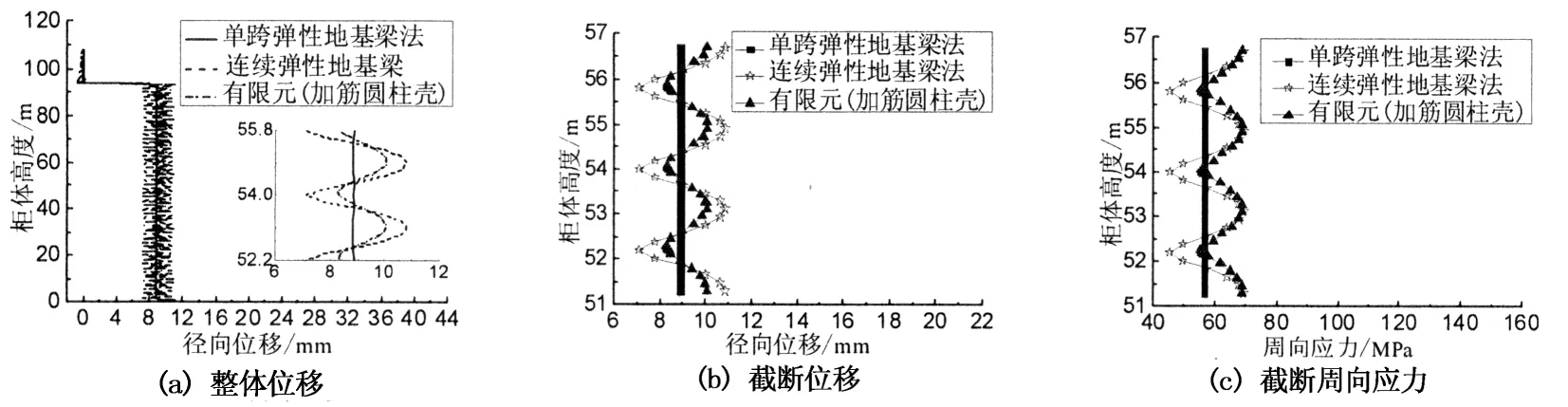
图11 弹性地基板条梁与有限元结果对比(dr =1.8 m)

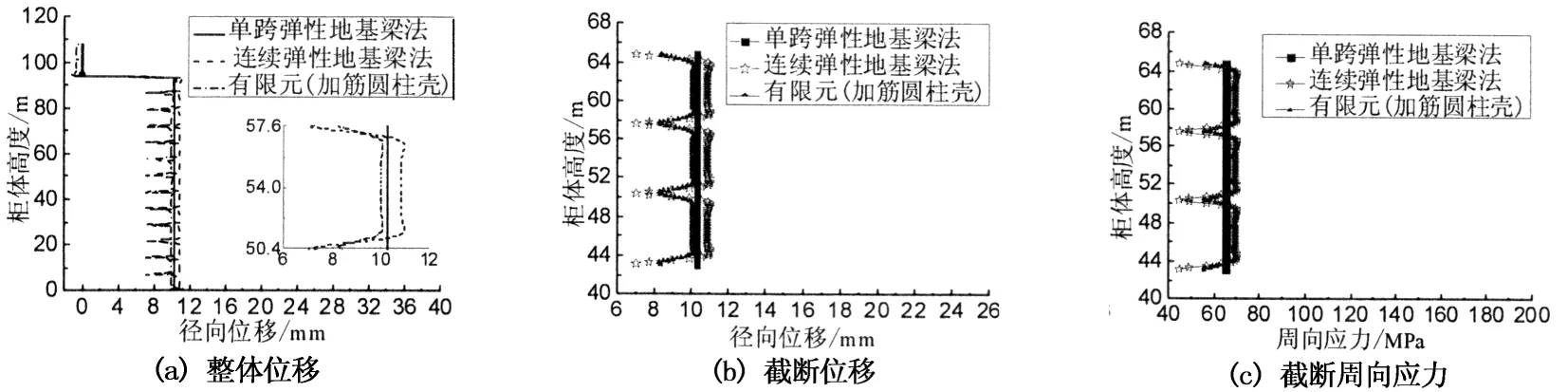
图12 弹性地基板条梁与有限元结果对比(dr =7.2 m)

图13 密加筋、单跨弹性地基梁与有限元结果对比(dr =1.2 m)

图14为改进离散加筋法、连续弹性地基梁法与有限元结果对比图.由图14可知，改进离散加筋法与连续弹性地基梁法结果均呈有规律较大波动，除少部分结果有偏差外，大部分结果与有限元结果是比较吻合的.改进离散加筋法结果与连续弹性地基梁结果有微小偏差，主要原因是前种方法计算时位移函数采用有限项级数逼近.

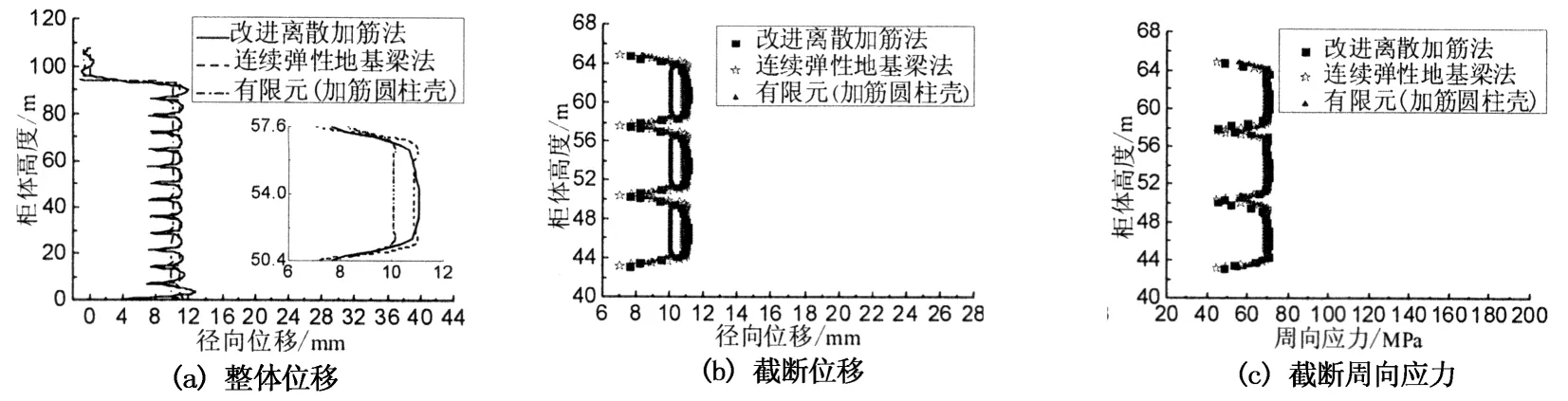
图14 改进离散加筋法、连续弹性地基梁法与有限元结果对比(dr =7.2 m)

3.5 密肋、稀肋建议公式

大型环向加筋圆柱壳结构参数如表1所示，对前面采用不同方法的dr参数化分析(见表3)得到：当肋间距dr≤2.524(Rh)1/2m时，适合采用密加筋法或单跨弹性地基板条梁法，可认为结构为环向密肋圆柱壳；当dr>2.524(Rh)1/2m时，应采用改进离散加筋法和连续弹性地基板条梁法，认为结构为环向稀肋圆柱壳.

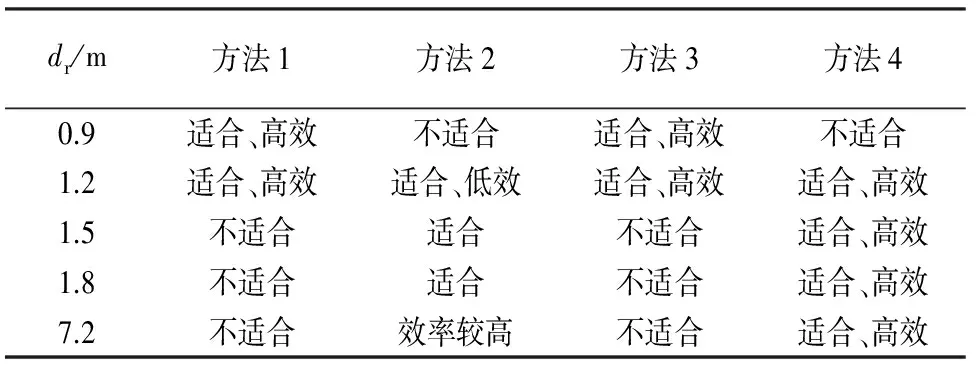
表3 环向加筋不同间距及方法对比

注：方法1为密加筋法；方法2为改进离散加筋法；方法3为单跨弹性地基板条梁法；方法4为连续弹性地基板条梁法.

4 结 论

1) 密加筋法等价于单跨弹性地基板条梁法.改进离散加筋法更能够体现加筋肋对结构的影响，当环向加筋间距dr>3.875 (Rh)1/2时计算效率较高.

2) 根据位移和应力结果的对比，判定环向加筋肋间距dr≤2.524(Rh)1/2时为环向密加筋圆柱壳，反之为环向稀加筋圆柱壳.

3) 弹性地基板条梁法可用于分析受局部内压作用、具有多根环向加筋大型圆柱壳结构的轴对称弯曲问题，较其他方法具有适用性强、精度高、效率好的优点.

[1] 谷中秀.新型干式煤气柜[M]. 北京:冶金工业出版社, 2010: 2-3,40-47,142.

GU Zhong-xiu. New typical gasholder[M]. Beijing: Metallurgical Industry Press, 2010: 2-3,40-47,142. (In Chinese)

[2] 姜德进. 正多边形干式贮气柜(M.A.N型)侧壁板在贮气压力下的内力分析[J]. 特种结构, 1986(3): 9-11.

JIANG De-jin. The internal force analysis of polygon dry gas storage tank (M.A.N-type) sidewall panels under gaspressure[J]. Special Structures, 1986(3): 9-11.(In Chinese)

[3] 姜德进. 干式煤气柜走道平台及立柱的内力计算[J]. 工业建筑, 1985(6): 20-23.

JIANG De-jin. The internal force calculation for walkway platform and column of dry gasholder[J]. Industrial Construction, 1985(6): 20-23. (In Chinese)

[4] 游理华. 曼型干式煤气柜柜体的计算理论与方法暨板的弹塑性弯曲和后屈曲分析[D].重庆：重庆建筑工程学院, 1989: 2-3.

YOU Li-hua. Theory and method for calculation for cabinet of MAN type dry gas holder and elastic-plastic bending and post-buckling of plate[D]. Chongqing:Chongqing Institute of Architecture and Engineering, 1989: 2-3. (In Chinese)

[5] 童根树,许钧陶.正多边形干式煤气贮柜的自振特性和地震响应分析[J]. 建筑结构学报, 1997, 18(5): 51-58.

TONG Gen-shu, XU Jun-tao. Natural vibration characteristics and earthquake response of MAN dry gasholders[J].Journal of Building Structures, 1997, 18(5): 51-58. (In Chinese)

[6] 周伟.新型煤气柜的强度和稳定性分析[D]. 重庆:重庆大学资源及环境科学学院, 2004:2-3.

ZHOU Wei. Strength and stability analysis of the typical gas tank[D]. Chongqing: Faculty of Resources and Environmental Science, Chongqing University, 2004:2-3. (In Chinese)

[7]但堂波. 曼型干式煤气柜的受力性能研究[D]. 杭州:浙江大学建筑工程学院, 2007:10-11.

DAN Tang-bo. Study on the structural behavior of MAN type dry gas holder[D]. Hangzhou: College of Civil Engineering and Architecture, Zhejiang University, 2007:10-11. (In Chinese)

[8] 贾冬云,曹平周,姜德进.正多边形气柜立柱结构简化分析方法研究[J]. 工程力学, 2010, 27(6): 252-256.

JIA Dong-yun, CAO Ping-zhou, JIANG De-jin. Study on simplified analytical method for the column of regular polygon gasholder[J]. Engineering Mechanics, 2010, 27(6): 252-256. (In Chinese)

[9] 贾冬云,曹平周,姜德进,等.大型正多边形气柜壳体的试验研究[J]. 土木工程学报, 2011, 44(8): 52-58.

JIA Dong-yun, CAO Ping-zhou, JIANG De-jin,etal. Experimental study of the shell of a large-scale regular polygon gasholder[J]. China Civil Engineering Journal, 2011, 44(8): 52-58. (In Chinese)

[10]姜德进,李伟.干式煤气柜若干问题的探讨[J]. 冶金动力, 2008,4: 19-22.

JIANG De-jin, LI Wei. Discussion on some problems of dry gasholder [J]. Metallurgical Power, 2008, 4:19-22.(In Chinese)

[11]肖为. 正交异性圆柱壳受局部外压时的稳定[J]. 应用力学学报, 1987, 4(4): 11-22.

XIAO Wei. Stability of orthotropic cylindrical shells under local external pressure[J]. Journal of Applied Mechanics, 1987, 4(4): 11-22. (In Chinese)

[12] 姜开春, 王德满. 加权参数法用于光滑和加筋旋转壳的静力分析[J]. 工程力学, 1987, 4(3): 44-57.

JIANG Kai-chun, WANG De-man. An application of M.W.R to the static analysis of smooth and reinforced circular shell[J]. Engineering Mechanics, 1987, 4(3): 44-57. (In Chinese)

[13]中国科学院力学研究所, 固体力学研究室板壳组. 加筋圆柱曲板与圆柱壳[M]. 北京: 科学出版社, 1983:2-3.

Institute of Mechanics, Chinese Academy of Sciences, Group of Solid Mechanics Research Shell. Stiffened cylindrical panels and cylindrical shells[M]. Beijing: Science Press, 1983:2-3. (In Chinese)

[14]BRUSH D O, ALMROTH B O. Buckling of bars, plates, and shells[M]. New York: McGraw-Hill, 1975:177-178, 272-276.

[15]王明贵,黄义.双向密肋壳体结构风稳定性研究[J]. 工程力学, 2000, 17(4): 44-49.

WANG Ming-gui, HUANG Yi. Stability of rib-reinforced cylindrical shells under wind load[J]. Engineering Mechanics, 2000, 17(4): 44-49.(In Chinese)

[16]PHILIPPE R. Applications des développements harmoniques au calcul des ouvrages hydrauliques métalliques[D]. Liege:Universite de Liege Faculte des Sciences Appliquees, 1989:25-42. (In French)

[17]徐芝纶. 弹性力学[M]. 3版.北京: 高等教育出版社, 1990: 268-274.

XU Zhi-lun. Elasticity[M]. 3rd ed. Beijing: Higher Education Press, 1990: 268-274. (In Chinese)

[18]熊俊,孟少平,周臻.大直径预应力混凝土煤仓在内压荷载下的受力分析[J]. 煤炭学报, 2010, 35(2): 222-226.

XIONG Jun, MENG Shao-ping, ZHOU Zhen. Analysis in wall stress of large-diameter prestressed concrete coal silo under internal pressure [J]. Journal of China Coal Society, 2010, 35(2): 222-226. (In Chinese)

[19]欧阳鬯,邱瑞强,张福保.关于承受轴压和侧压的离散偏心加筋圆筒的稳定性分析(I)——失稳前的弹性计算[J]. 复旦大学学报, 1975(2): 78-94.

OU Yang-chang, QIU Rui-qiang, ZHANG Fu-bao. Stability of discrete eccentric stiffening cylinder with stand axial and lateral pressure [J]. Journal of Fudan University, 1975(2): 78-94. (In Chinese)

[20]丁大钧,刘忠德.弹性地基梁计算理论和方法[M]. 南京: 南京工学院出版社, 1986 : 170-172.

DING Da-jun, LIU Zhong-de. The computational theory and method of beams on elastic foundation[M]. Nanjing: Nanjing Institute of Technology Press, 1986: 170-172. (In Chinese)

Study on the Bending Analytical Method for New Typical Gas Holder under Internal Pressure

LI Zheng-liang1, 2†,YU Wei1,HU Hao1,LIU Xin-peng1, WANG Ling-xi1

(1. College of Civil Engineering, Chongqing Univ, Chongqing 400045, China；2. Key Laboratory of New Technology for Construction of Cities in Mountain Area (Chongqing Univ), Ministry of Education, Chongqing 400045, China)

The bending of a new typical gas holder under gas pressure is crucial to ensure the normal operation of the structure. It can be simplified to elastic bending of ring stiffened cylindrical shell, which is under partial internal pressure and has multiple circular reinforced ribs. Stripe Beam on Elastic Foundation Method (SBEFM) was extendable to the structure system. At the same time, traditional discrete stiffened method (TDSM) was improved. A gas holder of 300 000 m3was taken as an example for analysis. On this basis, the method judging ring stiffened cylindrical shell smeared or discrete was presented. The new analysis shows that SBEFM has a wider applicability, higher accuracy and better efficiency than other methods and the improved discrete stiffened method is effective when the ring spacing is greater than 3.875 (Rh)1/2.

thin walled structures; gas holders; stripe beam on elastic foundation method; improved discrete stiffened method; affected width

1674-2974(2015)01-0053-09

2014-04-06

国家自然科学基金资助项目(51278511)，National Natural Science Foundation of China(51278511)

李正良(1963-)，男，江苏江阴人，重庆大学教授，博士生导师†通讯联系人，E-mail:lizhengl@hotmail.com

TU392.2

A