“顶吸基隔”结构非平稳随机地震反应分析新方法

马涌泉，邱洪兴

(东南大学 土木工程学院，江苏 南京 210096)

“顶吸基隔”结构非平稳随机地震反应分析新方法

马涌泉†，邱洪兴

(东南大学 土木工程学院，江苏 南京 210096)

为了有效抑制基础隔震结构的隔震层及主结构的过大位移，设计了“顶吸基隔”减震结构并提出了相应的非平稳随机反应分析新方法.通过在基础隔震结构的顶部布置调谐质量阻尼器来构建减震结构，分别采用Bouc-Wen模型及其刚度退化模型模拟隔震层及各楼层的滞回特性.通过在精细积分法中引入复化Cotes积分，并结合虚拟激励法，提出了求解减震结构非平稳随机反应的CCIM法.依据首次超越破坏准则，建立了以结构层间位移角为评价指标的动力可靠度极限状态方程.通过分别采用CCIM、蒙特卡罗法和时域显式蒙特卡罗法对减震结构进行随机反应分析，验证了CCIM具有高效率和高精度的特点.以一座30层钢框架结构为算例，分别计算了减震结构、基础隔震结构和未控制结构在8度和9度罕遇地震作用下的随机反应.结果表明：本文提出的“顶吸基隔”减震结构的整体可靠度比基础隔震结构和未隔震结构的都要高，该减震结构具有极大的工程推广价值.

建筑物；抗震设计；地震反应；调谐质量阻尼器；精细积分法；动力可靠度

随着中国城镇化建设步伐的加快，各地兴建了为数不少的高层建筑，如何提升它们的抗震性能，一直是学者们研究的重点.基础隔震作为一项有效的减震技术，在高层结构中正得到普遍应用，但其隔震层在震后会产生较大变形[1].虽然可以通过在隔震层中增设阻尼器或限位器来减小或限制其位移，但会引起主结构层间位移的增大[2].在基础隔震结构中引入调谐质量阻尼器(TMD)组成“TMD-基础隔震”结构可以解决隔震层及主结构位移均较大的难题，本文将这种结构命名为“顶吸基隔”减震结构(简称减震结构).学者们对该结构的减震效果进行过一些研究[3-4]，但这些研究均是输入确定的地震动来求解结构反应，由于地震动具有随机性，因此这些研究成果缺乏参考价值；目前学者们仅开展了基础隔震结构随机反应的求解工作[5-6].然而他们所采用的精细积分法在计算过程中会存在矩阵求逆的问题，不仅计算量大，而且稳定性也较差，甚至会出现逆矩阵不存在的情况.因此探寻减震结构非平稳随机反应的高效率和高精度的求解方法就显得尤为重要.本文采用Bouc-Wen模型及其刚度退化模型描述隔震层及楼层的滞回特性，利用精细积分法和虚拟激励法推导出复化Cotes精细积分法(CCIM)，并验证了其精度和效率.使用CCIM分别对一座30层减震、基础隔震和未隔震结构进行非平稳随机反应与动力可靠度分析，得出的结论可供类似结构减震设计时参考.

1 减震结构计算模型

1.1 减震结构运动方程

减震结构是在基础隔震结构的顶部布置TMD，利用TMD可以调谐结构频率的特点，对主结构施加一个与振动方向相反的力，从而达到吸收地震能量和降低结构反应的目的.减震结构的力学模型见图1.

图1 减震结构的力学模型

该减震结构的非线性运动方程可表示为：

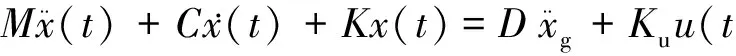
(1)

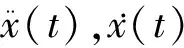
(2)

(3)

K=

(4)

Ku=

(5)

式(2)～式(5)中：mb,mn和mt分别为隔震层、第n楼层和TMD的质量；cb,cn和ct分别为隔震层、主结构第n层和TMD的阻尼；kb,kn和kt分别为隔震层、主结构第n层和TMD的刚度；ηb,ηn和ηt分别为隔震层、主结构第n楼层和TMD的第二刚度系数.

分别采用Bouc-Wen模型及其刚度退化模型[7]模拟隔震层和楼层的滞回特性，它们的表达式分别为：

(6)

(7)

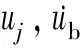
式(1)的状态方程可表示为：

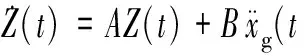
(8)

向量Z(t),A和B可分别表示为：

(9)

式中：Ce和Ke皆为减震结构滞回模型的等效线性化系数矩阵.λ可表示为：

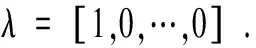
(10)

1.2 滞回模型的等效线性化

将滞回位移关系式(6)和式(7)表示为：

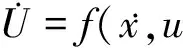
(11)

将滞回位移向量U看作已知随机状态反应，则式(11)的等效线性化方程可表示为：

(12)

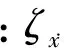
(13)

(14)

Gj,μ和α可分别表示为:

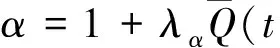
(15)

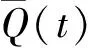
(16)

L1,L2,L3和L4可分别表示为：

(17)

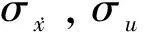
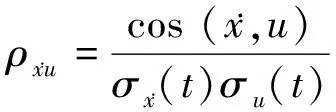
(18)

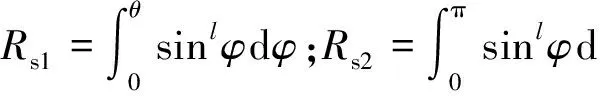
(19)

其中φ为：

(20)

2 非平稳随机反应与动力可靠度分析

2.1 虚拟激励的构造

非平稳随机地震激励过程h(t)可描述为平稳随机过程g(t)与调制函数r(t)的乘积，即

h(t)=g(t)r(t)．

(21)

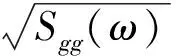
(22)

则t时刻结构的随机反应可表示为：

(23)

式中：R(ω,t)为确定性地震激励对初始静止结构在t时刻所产生的反应.因此可以得到：

(24)

式中：R*(ω,t)与R(ω,t)互为共轭函数.

则结构反应y(ω,t)的自谱密度函数Syy(ω,t)可表示为：

(25)

依据式(25)求得Syy(ω,t)．结构反应y(ω,t)的方差可表示为：

(26)

(27)

2.2 复化Cotes数值积分法

结构状态方程(8)的一般解为：

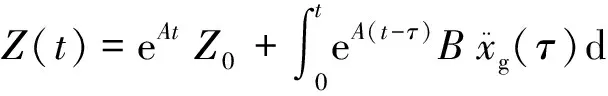
(28)

将随机地震激励在时间域上离散为若干个区间，步长为Δt，由式(28)可推出任一时刻tl+1的结构反应为：

(29)

令式(29)中的指数矩阵满足eAΔt=T(Δt)=T，T的精细算法详见文献[9]，因此式(29)可记为：

(30)

精细积分中的指数矩阵T(Δt)经过精细计算以后，可以使得其值非常接近精确值，但是其积分项解析形式的精度仍不能保证.文献[10]将精细积分法引入随机地震反应分析，提出了时域显式蒙特卡罗法(PTIM)，它假定地震激励在(tl,tl+1)内线性变化，但当地震激励具有强非线性时这种算法会带来较大误差，如果通过减小时间步长Δt来提高计算精度，势必会增加计算量.文献[11]在结构随机反应分析中引入了Simpson积分，虽然提高了结构反应的精度，但由于该积分方法的固有缺陷，只能达到三次代数精度.为了解决上述问题，本文引入复化Cotes积分理论来求解结构随机反应一般解的积分项，提出了一套基于复化Cotes理论的精细积分法，并将其命名为CCIM.该方法既能良好地处理非线性地震激励，又能获得比Simpson积分更高的精度，并且对Δt也不敏感.

CCIM的建立过程如下：将复化Cotes积分引入式(30)，积分区间分点为tk=tl+kh(k=0,1,…,m)，可得：

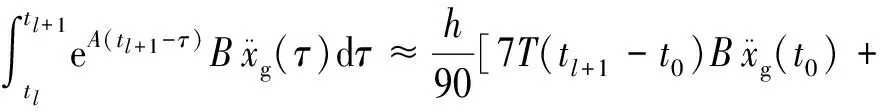
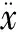
(31)

将式(31)中的求和项展开，并整理同类项形成随机地震激励列向量ρl, l+1和系数矩阵O.ρl, l+1的下标表示积分区间[tl,tl+1]，ρl, l+1和O可分别表示为：

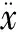
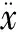
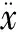
(32)

12T(tl+1-t1/2)·32T(tl+1-t3/4)×

7T(tl+1-t1)…32T(tl+1-t(m-1)/4)×

12T(tl+1-t(m-1)/2)·32T(tl+1-t3(m-1)/4)×

7T(tl+1-tm)]．

(33)

由式(33)可知，O矩阵的组成由复化次数m决定，复化Cotes积分法在积分区间采用均等分形式，且积分区间[tk,tk+1]被等分为4份，因此时间段[tk,tk+1]共被划分为4m份，每份时长为Δt/4m，式中任一积分点的指数矩阵Ti可表示为：

Ti=(eAΔt/4m)i．

(34)

可见只需求解指数矩阵T(Δt/4m)=eAΔt/4m，并结合指数矩阵的加法原理便可求得矩阵O的数值.

不考虑误差项，式(31)可表示为：

(35)

将式(35)代入式(30)，可得：

Z(tl+1)=TZ(tl)+Oρl,l+1．

(36)

当初始条件Z(t0)=0，可推导出结构反应Z(tl)的表达式：

(37)

令

(38)

因此Z(tl)也可表示为：

Z(tl)=Ylρl．

(39)

上式即为求解结构反应的显式表达式.结合一阶矩和二阶矩的运算特点，可得Z(tl)的期望及方差分别为：

(40)

式(40)中的协方差矩阵可由随机地震激励的相关函数构成，相关系数可由式(18)求得.

相邻时刻的系数矩阵存在以下递推关系：

Yl+1=[TYlO]．

(41)

综上所述，按照式(38)构造出该时刻的ρl和Yl便可求得tl时刻的结构反应Z(tl)；如果求解(tl,tl+1)时间段内的Z(tl)，只需结合式(41)便可较快地获得各时刻点的系数矩阵.

上述CCIM法的推导虽然是以剪切型结构为例，但是此算法是以精细积分法和复化Cotes积分理论为基本框架，因此它对结构的动力特性矩阵没有任何特殊要求，故此算法完全适用于求解弯剪型或弯曲型结构的非平稳随机地震反应.

2.3 结构层间位移角可靠度分析

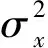
(42)

当结构反应为非平稳过程时，则层间位移角的对称双侧动力可靠度Ωs为：

(43)

结构层间位移角的失效概率为：

Ωf=1-Ωs．

(44)

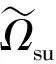
(45)

(46)

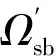
3 CCIM精度与效率的验证

为了验证CCIM的计算精度及效率，本文选用一座10层钢框架结构为算例.该算例位于Ⅱ类场地，抗震设防烈度为8度，设计基本地震加速度值为0.30g，处于设计地震第1组.首先对其进行8度罕遇地震作用下的基础隔震设计，获得隔震层的各项最优参数；然后对基础隔震结构进行模态分析获得其前10阶自振频率，以此获得TMD系统的各项最优参数(保证TMD系统的前10阶自振频率与基础隔震结构的分别相等或十分接近)；最后对减震结构进行模态分析，提取其前三阶阻尼比，并取它们的平均值作为该结构的阻尼比.分别运用蒙特卡罗法[12](M-C)、CCIM和PTIM对减震结构进行8度罕遇地震作用下的非平稳随机地震反应分析.

隔震层高度为1.8 m，上部各楼层高度均为3.0 m，减震结构的阻尼比ξs8=0.017；Bouc-Wen模型的参数取值为：d=1，G=1，γ=0.8，β=0.2，ηb=0.4.隔震层的最优参数为：质量mb=9.0×104kg，刚度kb=7.0×107N·m-1，阻尼cb=2.0×105N·s·m-1；Bouc-Wen刚度退化模型的参数取值为：d=0.9，G=1.1，γ=0.7，β=0.25，λG=0，λμ=0，λα=0.000 1，η1～ηn=0.12.各楼层的质量mj=2.0×105kg，各楼层的刚度kj=6.0×108N·m-1；TMD系统的最优参数为：质量mt=5.0×104kg，刚度kt=1.2×106N·m-1，阻尼ct=1.5×105N·s·m-1.

本文采用Clough-Penzien模型[13]来模拟平稳随机地震动功率谱，其功率谱密度函数可表示为：

(47)

式中：S0为谱强度因子；ωf和ζf为描述地震动低频能量变化的参数；ωg和ζg分别为场地土的卓越频率和阻尼比，它们与规范[14]中的场地类别和设计地震分组有一一对应的关系．为了考虑该模型参数的不确定性对结构反应的影响，本文依据地震波的平均反应谱与设计反应谱在主周期点的谱值相差不超过20%，地震动有效持时为结构基本周期的5～10倍，时程分析结果在结构主方向的平均底部剪力应处于振型分解反应谱法的80%～120%之间，以及单条地震波的结构底部剪力应处于振型分解反应谱法的65%～135%之间等四项原则选取了80组(每组有2个水平向分量，震级范围为5～9级，震中距范围为0～200 km，场地类别为Ⅱ类)地震加速度时程记录，对该模型参数进行了计算，求得了Ⅱ类场地的ωg和ζg的变异系数ηω=0.397和ηω=0.392，并分别乘以文献[15]提供的ωg和ζg的参考值，最终得到该模型参数为：ωg=17.95 rad/s；ωf=3.49 rad/s；ζf=ζg=0.72；8度罕遇地震的S0=3.129 cm2·s-3.

调制函数r(t)可表示为：

(48)

式中：ε为衰减系数；t1和t2分别为主振平稳段的首末时间.Ⅱ类场地的t1=0.8 s,t2=7.0 s,ε=0.35.

表1为分别采用3种算法获得的减震结构随机反应方差峰值.由表中可以看出，当步长Δt=0.1 s时，采用复化次数m=1的CCIM与M-C的计算结果非常接近，且前者所需的计算时间比后者要少得多.此步长下PTIM的计算结果平均误差较小，所需的计算时间比m=1时CCIM的要多一些；当步长Δt=0.5 s时，PTIM的计算结果已严重偏离M-C的结果，前者的平均误差达到了53.26%，其结果已没有任何参考价值.此步长下的m=1时的CCIM，其计算结果也偏离了M-C的结果，平均误差为11.76%，结果同样失真；保持步长Δt=0.5 s不变，仅将m调至2，此时CCIM的计算结果再次与M-C法非常接近，前者的结果稍微偏保守.而且从m=1调至m=2时，计算时间并没有太明显的增加，仍比M-C的计算时间少很多.

可见，本文提出的CCIM对步长有弱敏感性，在步长不变的情况下，增大复化次数可以提高计算精度，并且不会引起计算时间的大幅增加.当步长相同时，CCIM的计算精度比PTIM的要高得多，前者的计算结果非常接近M-C法，但CCIM所需的计算时间比M-C要少很多.因此，CCIM在求解减震结构非平稳随机反应方面具有高精度和高效率的特点.

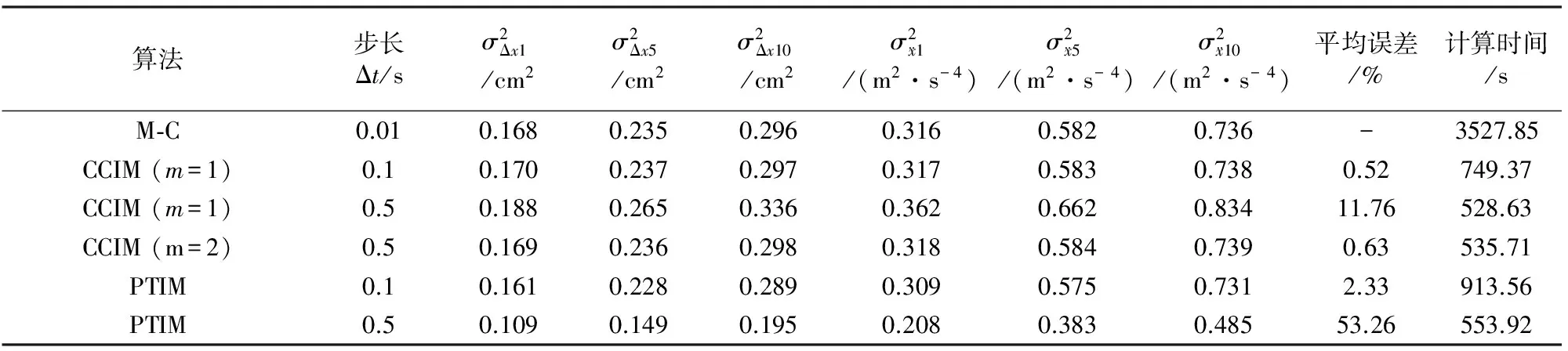
表1 不同算法得到的减震结构随机反应方差峰值

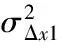
4 数值分析

4.1 工程背景

选取一座位于Ⅱ类场地的30层钢框架公寓为工程背景，设烈度8度，设计基本地震加速度值为0.30 g，处于设计地震第1组.首先分别建立减震、基础隔震和未隔震结构模型；然后运用本文第3节的方法分别对基础隔震及减震结构进行8度和9度罕遇地震作用下的优化设计，获取隔震层和TMD系统的各项最优参数以及结构阻尼比.最后采用CCIM分别计算8度和9度罕遇地震下的3种结构随机反应及层间位移角动力可靠度.

该公寓的隔震层高度、楼层高度、Bouc-Wen模型及其刚度退化模型的参数值均与算例相同.各楼层刚度kj的取值见表2.ωg,ωf,ζg,ζf,t1,t2和ε的值与上节算例的相同.8度和9度罕遇地震下施加于各结构的谱强因子S0的取值见表3.

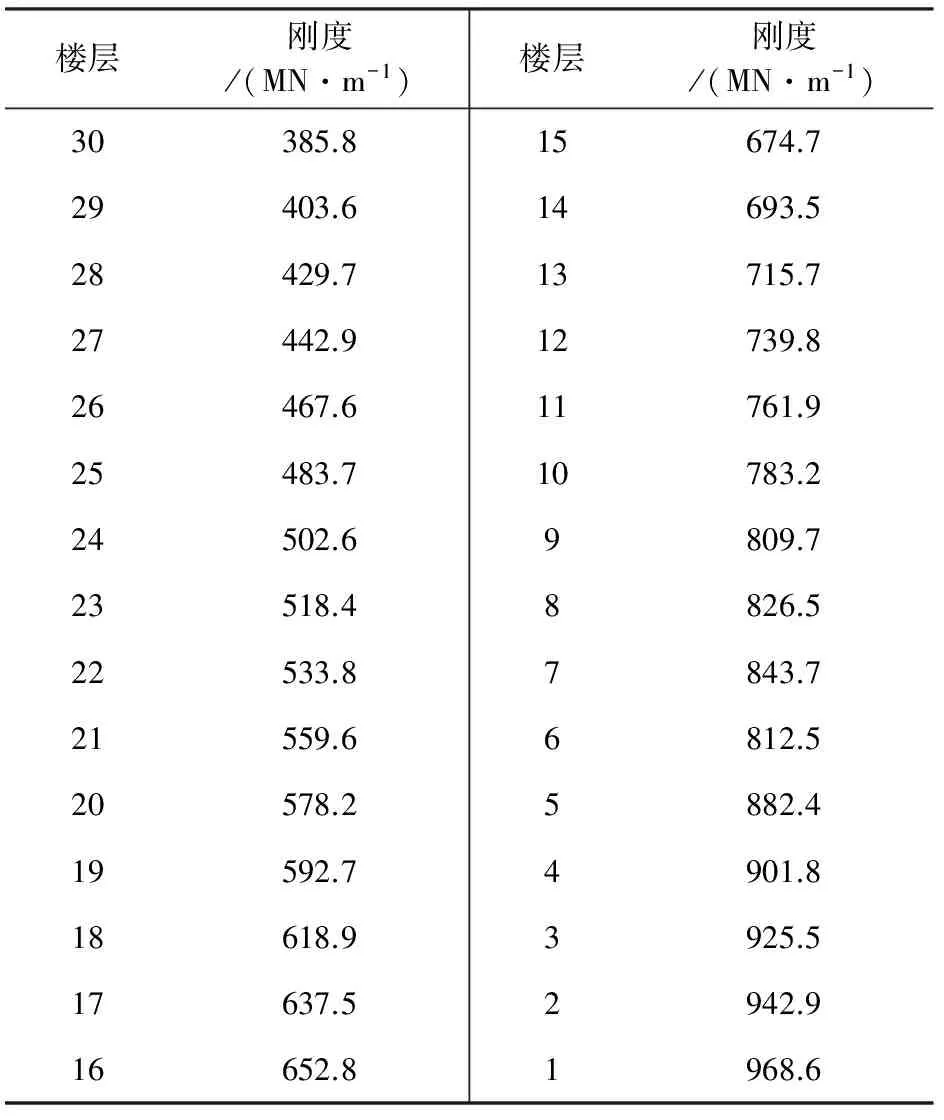
表2 各楼层刚度的取值

表3 谱强因子S0的取值

Tab.3 Values of spectral intensity factorS0

(cm2·s-3)

8度罕遇地震作用下的隔震层的最优参数为：质量mb=1.528×105kg，刚度kb=1.363×108N·m-1，阻尼cb=2.963×105N·s·m-1.9度罕遇地震下的隔震层的最优参数为：质量mb=1.861×105kg，刚度kb=1.537×108N·m-1，阻尼cb=3.285×105N·s·m-1；各楼层的质量mj=3.672×105kg；8度罕遇地震下的TMD系统的最优参数为：质量mt=8.685×104kg，刚度kt=9.573×106N·m-1，阻尼ct=6.791×105N·s·m-1.9度罕遇地震下的TMD系统的最优参数为：质量mt=9.352×104kg，刚度kt=9.976×106N·m-1，阻尼ct=7.163×105N·s·m-1；8度和9度罕遇地震作用下的减震、基础隔震及未隔震结构的阻尼比分别为ξs8=0.016和ξs9=0.017，ξj8=0.013和ξj9=0.014及ξw8=0.019和ξw9=0.020.各楼层的弹性层间位移角限值θb1=1/550 rad，隔震层的塑性层间位角限值θb2=1/18 rad.

定义8和9度罕遇地震下的减震结构分别为工况Ⅰ和Ⅱ，8和9度罕遇地震下的基础隔震结构分别为Ⅲ和Ⅳ，8和9度罕遇地震下的未隔震结构分别为Ⅴ和Ⅵ.采用CCIM分别对6种工况进行非平稳随机分析，得到顶层位移、第6层层间位移角及顶层加速度等方差时程如图3所示.得到隔震层和各楼层的位移、层间位移角及加速度等方差峰值及层间位移角可靠度如图4～图5所示.

4.2 结果分析

由图3可知，在整个时程内，减震结构的位移方差、层间位移角方差和加速度方差比基础隔震和未隔震结构的方差都要小.6种工况的反应方差均能在较短的时间内收敛到一个稳定的解，说明本文提出的CCIM具有良好的稳定性，此方法可用于评估高层或多层结构在非平稳随机地震作用下的抗震性能.

T/s(a) 顶层位移方差时程

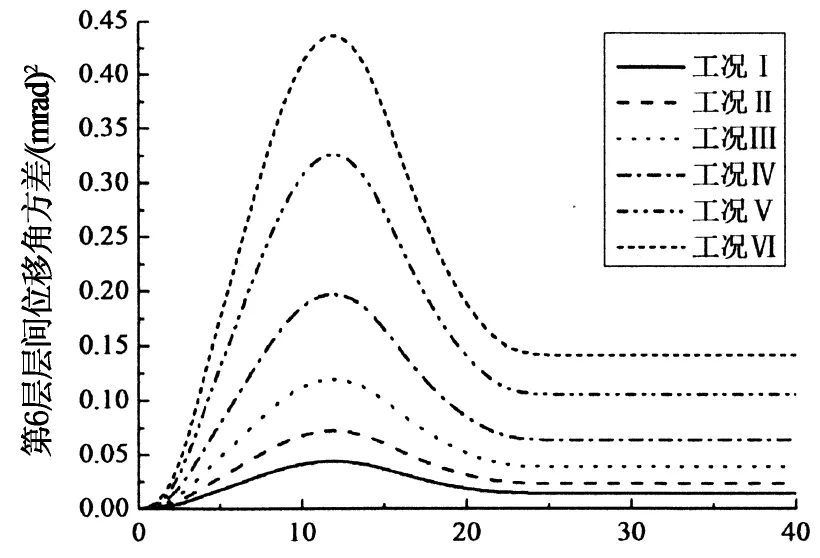
T/s(b) 第6层层间位移角方差时程

T/s(c) 顶层加速度方差时程

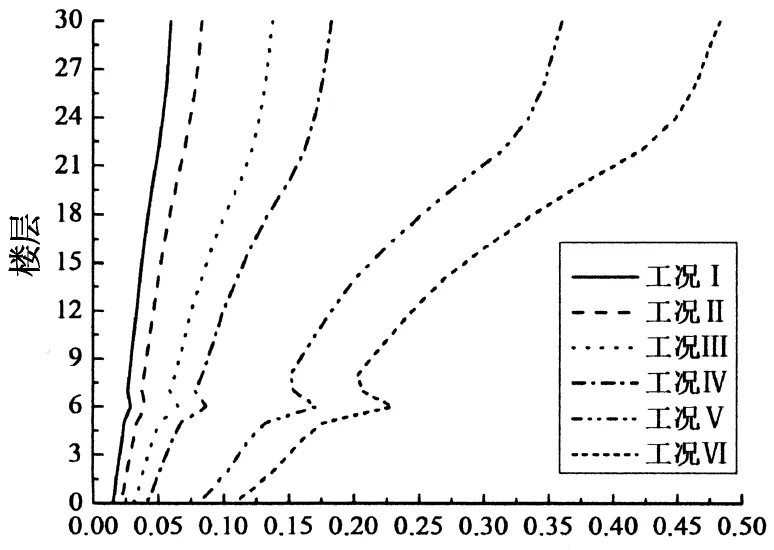
位移方差峰值/m2(a) 隔震层和各楼层的位移方差峰值

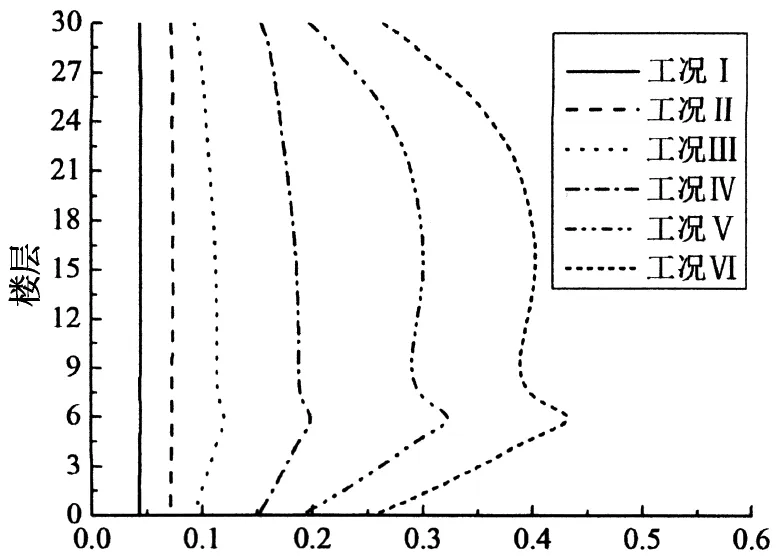
层间位移角峰值/(mrad)2(b) 隔震层和各楼层的层间位移角方差峰值

加速度方差峰值/(m2·s-4)(c) 隔震层和各楼层的加速度方差峰值

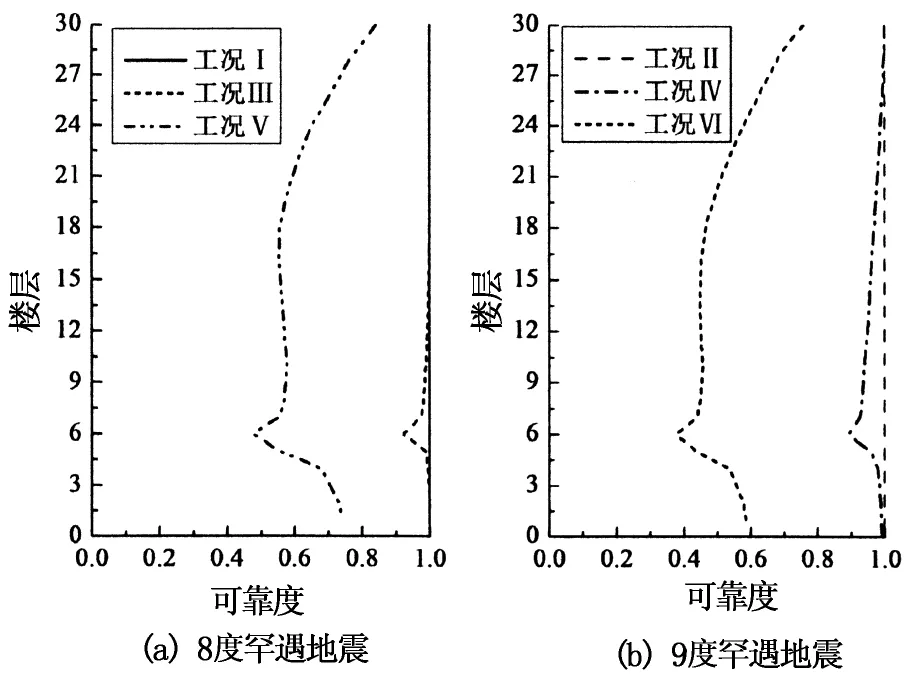
图5 隔震层和各楼层的层间位移角可靠度

由图4可知，减震结构的隔震层和各楼层位移方差峰值、层间位移角方差峰值和加速度方差峰值均比基础隔震和未隔震结构(无隔震层)的要小；6种工况的上述三项值在第6层处均存在不同程度的转折，其中减震结构的转折程度最不明显.这是由于原结构的第6层刚度有突变，形成了薄弱层.可见，通过在基础隔震结构顶部布置TMD而形成的减震结构可以有效解决隔震层及主结构在震后出现过大位移的难题.

由图5可知，减震结构无论是在8度还是9度罕遇地震下，其隔震层和各楼层的层间位移角可靠度均为100%；8度和9度罕遇地震下的基础隔震结构其隔震层和各楼层的层间位移角可靠度也均较高，根据式(46)算得其整体可靠度分别为95.53%和91.76%，但第6层处的可靠度有一定的降低，可见结构刚度的突变对基础隔震结构的层间位移角可靠度有一定的影响；8度和9度罕遇地震下的未隔震结构其各楼层的层间位移角可靠度很低，在第6层处达到了最低，根据式(45)算得其整体可靠度分别为58.82%和46.91%，因此在9度罕遇地震下，未隔震结构的大多数层间位移角已超过了弹性层间位移角限值.可见在罕遇地震作用下，减震结构的整体可靠度比基础隔震和未隔震结构的都要高得多.

5 结 论

1) 本文提出的CCIM其计算精度和计算效率要比PTIM的都要高，其计算结果逼近M-C的结果，而CCIM所需的计算时间却比M-C的要少得多；CCIM能使结构反应方差在较短时间内收敛到稳定解.可见，本文提出的CCIM兼备高效率和高精度的特点，可望有极佳的工程应用前景.

2) 减震结构的楼层及隔震层位移、层间位移角和加速度方差比基础隔震结构的都要小，前者的整体可靠度比基础隔震和未隔震结构的都要高；薄弱层的存在对减震结构的整体可靠度几乎没有影响.可见，本文提出的“顶吸基隔”减震结构具有卓越的抗震性能，可望有良好的工程推广价值.

[1] ARIGA T, KANNO Y, TAKEWAKI I. Resonant behaviour of base-isolated high-rise buildings under long-period ground motions[J]. The Structural Design of Tall and Special Buildings, 2006, 15(3): 325-338.

[2] SPENCER B F, NAGARAJAIAH S. State of the art of structural control[J]. Journal of Structural Engineering, 2003, 129(7): 845-856.

[3] TANIGUCHI T, KIUREGHIAN A D, MELKUMYAN M. Effect of tuned mass damper on displacement demand of base-isolated structures[J]. Engineering Structures, 2008, 30(12): 3478-3488.

[4] DE I M, PETTI L, PALAZZO B. Combined control strategy base isolation and tuned mass damper: an effectiveness analysis of its application to non-linear benchmark base isolated structure[C]//Proceedings of the 14th World Conference on Earthquake Engineering. Beijing: Science Press, 2008: 129-138.

[5] 马长飞, 张亚辉, 谭平, 等. 三维非偏心基础隔震结构非平稳随机振动分析[J]. 工程力学, 2013, 30(4): 198-203.

MA Chang-fei, ZHANG Ya-hui, TAN Ping,etal. Non-stationary stochastic analysis for 3D non-eccentric base-isolated buildings[J]. Engineering Mechanics, 2013, 30(4): 198-203. (In Chinese)

[6] JANGID R S. Stochastic response of building frames isolated by lead-rubber bearings[J]. Structural Control and Health Monitoring, 2010, 17(1): 1-22.

[7] ERLICHER S, BURSI O S. Bouc-Wen-Type models with stiffness degradation: thermodynamic analysis and applications[J]. Journal of Engineering Mechanics, 2008, 134(10): 843-855.

[8] LIN Jia-hao, ZHANG Wen-shou, WILLIAMS F W. Pseudo-excitation algorithm for nonstationary random seismic responses[J]. Engineering Structures, 1994, 16(4): 270-276.

[9] ZHONG Wan-xie. On precise integration method[J]. Journal of Computational and Applied Mathematics, 2004, 163(1): 59-78.

[10]ZHANG Ya-hui, LI Qiu-sheng, LIN Jia-hao,etal. Random vibration analysis of long-span structures subjected to spatially varying ground motions[J]. Soil Dynamics and Earthquake Engineering, 2009, 29(4): 620-629.

[11]POULIMENOS A G, FASSOIS S D. Parametric time-domain methods for non-stationary random vibration modelling and analysis-a critical survey and comparison[J]. Mechanical Systems and Signal Processing, 2006, 20(4): 763-816.

[12]PROPPE C, PRADLWARTER H J, SCHUELLER G I. Equivalent linearization and Monte Carlo simulation in stochastic dynamics[J]. Probabilistic Engineering Mechanics, 2003, 18(1): 1-15.

[13]SEGHIR M. Generalized minimum variance gain scheduling controller for nonlinear structural systems under seismic ground motion[J]. Journal of Electrical Systems, 2012, 8(4): 472-480.

[14]GB 50011-2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010: 172-176.

GB 50011-2010 Code for seismic design of buildings[S]. Beijing: China Architecture and Building Press, 2010: 172-176. (In Chinese)

[15]薛素铎, 王雪生, 曹资. 基于新抗震规范的地震动随机模型参数研究[J]. 土木工程学报, 2003, 36(5): 5-10.

XUE Su-duo, WANG Xue-sheng, CAO Zi. Parameters study on seismic random model based on the new seismic code[J]．China Civil Engineering Journal, 2003, 36(5): 5-10. (In Chinese)

A New Method for Analyzing the Non-stationary Random Seismic Responses of Structure with Top-absorption and Base-isolation

MA Yong-quan†, QIU Hong-xing

(College of Civil Engineering, Southeast Univ, Nanjing, Jiangsu 210096, China)

To effectively suppress the larger displacement of both the isolation layer and the main structure of base-isolation structures, the top-absorption and base-isolation type seismic reduction structure (SRS) was designed, and a new non-stationary random seismic response analysis method applied to this structure was also presented. This seismic reduction structure was constructed by installing a tuned mass damper on the top of a base-isolation structure, and the hysteretic properties of both the isolation layer and each storey were simulated in Bouc-Wen and Bouc-Wen stiffness degradation model. The CCIM, which was applied to solve the non-stationary random response of SRS, was presented by introducing the composite Cotes integral into precise integral method and combining the pseudo excitation method. The dynamic reliability limits state equation, which took structural inter-storey displacement angle as the evaluation index, was established on the basis of the first excursion failure criterion. Both the high efficiency and the high precision of the CCIM were validated by computing the random seismic response of SRS and comparing CCIM's results with those of Monte Carlo method and time domain explicit Monte Carlo method, respectively. Taking the 30-storey steel frame structure as a numerical example, the random seismic response of SRS, base-isolation and non-isolation structures subjected to 8 and 9 degrees rare earthquake were computed, respectively. The analysis results indicate that the whole reliability of SRS presented is higher than those of base-isolation and non-isolation structures, and this SRS has great value in practical engineering.

buildings; seismic design; seismic response; tuned mass damper; precise integral method; dynamic reliability

1674-2974(2015)01-0031-09

2014-03-03

国家自然科学基金资助项目(51078077),National Natural Science Foundation of China(51078077)；“十二五”国家科技支撑计划资助项目(2012BAJ14B00)

马涌泉(1984-)， 男, 山东安丘人, 东南大学博士研究生†通讯联系人，E-mail:lemon9143@163.com

O328; TU352.1

A