锤击作用下钢筋混凝土框架倒塌性能试验研究

何庆锋，刘义仁，蒋曲翀，易伟建

(湖南大学 土木工程学院，湖南 长沙 410082)

锤击作用下钢筋混凝土框架倒塌性能试验研究

何庆锋†，刘义仁，蒋曲翀，易伟建

(湖南大学 土木工程学院，湖南 长沙 410082)

为研究钢筋混凝土平面框架结构在局部构件失效后的静、动力特性，完成了两榀两跨单层平面框架试验，其中一榀框架用于静载试验以获取框架静力特性数据，另一榀框架分别在空载、均布线荷载情况下采用锤击法进行动力试验，获取试验框架的位移、加速度和钢筋应变等动力响应数据．通过对比分析静载与动力试验结果，研究框架梁在锤击过程中的受力特性．试验结果表明：在大当量力锤锤击作用下，动力位移幅值与输入冲量近似呈线性关系，随着锤击力的增加，结构阻尼变化较小，频率下降．布有均布线荷载的框架梁在锤击荷载作用下产生了拱效应，刚度略有提高．尽管力锤最大锤击力超过框架梁最大抗力，但冲击能量不可使其发生倒塌．

钢筋混凝土框架；锤击法；动力效应；连续倒塌

近年来，结构连续倒塌(Progress Collapse)分析与设计在国内外已成为研究热点[1-8].结构发生连续倒塌，主要原因是爆炸、恐怖袭击等偶然荷载作用下建筑结构局部支撑构件的突然失效.局部支撑构件的突然失效会在周围构件上产生动力效应，失效构件承担的荷载通过横向传力构件传递给周围支撑构件，若周围支撑构件能承受这些荷载并达到新的受力平衡状态，结构将不会发生倒塌，否则，结构将发生连续倒塌.

DOD[9]抗倒塌设计指南中采用直接和间接两种方法进行抗倒塌设计.备用荷载路径法是常用的一种直接分析方法，该方法假定局部支撑构件失效，然后对剩余结构进行抗倒塌分析，其采用的分析方法主要有静力线性、静力非线性、动力线性以及动力非线性分析方法.静力分析方法简单但没有考虑连续倒塌过程中的动力效应问题，计算结果不够精确，动力分析方法精确但需对结构进行动力时程分析，其过程复杂且需较高时间成本．有研究表明[1], 基于合理动力放大系数，采用静力等效分析方法可得到精确的计算结果以指导设计.现有抗倒塌设计指南均采用动力放大系数2.0，不少研究者对框架结构进行了动力分析和计算[2-4].

结构发生连续倒塌是一个复杂的动力效应过程，不仅包含动力非线性效应，还伴随构件碰撞等现象，且相关试验研究较少.本文在此背景下，对两榀平面框架展开试验研究,第1榀框架通过静载试验来获取框架结构的静力特性数据，如框架的抗力位移曲线、破坏特征以及受力特性等；第2榀框架拟采用锤击法进行动力试验，获取框架梁在中间柱头上受不同当量锤击荷载作用下的动力特性，并采用有限元软件SAP2000对试验结构进行动力时程分析.

1 试验设计

按照GB 50010- 2010《混凝土结构设计规范》[10]和GB 50011-2010《建筑抗震设计规范》[11]，设计并在相同的条件下制作了两榀比例为1∶3的单层两跨平面框架模型，配筋以及截面尺寸都一样.其中一榀模型框架用于拟静力试验，以获取框架结构的静力特性数据，另一榀模型框架基于锤击法完成动力性能试验，获取框架结构的动力特性数据.钢筋的搭接以及锚固、箍筋间距均按照规范要求施工，框架配筋信息以及动力试验仪器布置如图1所示，静载试验框架主要测得中间柱头竖向荷载-位移曲线.

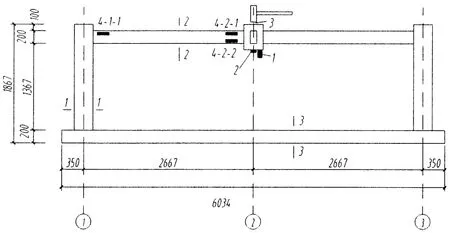
(a)试验框架尺寸及测点布置图

(b)1-1截面 (c)2-2截面 (d)3-3截面

试验框架梁柱纵向受力钢筋均为HRB400级钢筋，混凝土强度等级为C30.施工过程为先浇筑地基梁然后浇筑柱、梁.钢筋及混凝土的力学性能指标实测值如表1所示.

表1 钢筋及混凝土的力学性能指标实测值

试验框架通过地脚螺栓固定在实验室地基梁上.试验之前，中柱采用千斤顶代替，如图2所示.对于静载试验框架，移除千斤顶后，采用机械式千斤顶在框架中间柱头顶部对框架施加竖向荷载，加载过程分级采用位移控制，每级加载后，读取框架中间柱头竖向位移.

动力试验分两种情况实施，第1种为空载框架，第2种为均布线荷载框架，即对布有1.2 kN/m线荷载(采用结构胶将砝码粘结在试验框架梁上，如图3所示)的框架进行锤击试验.试验时将框架中间柱头下部千斤顶移除，用重型力锤手工锤击框架中间柱头上表面中心位置，如图4所示，锤击过程中人工控制锤击力，锤击力由小至大连续增加到最大锤击力.采用位移计和加速度计测取中间柱头动位移和加速度，如图1所示，并同时测得力锤锤击荷载以及框架梁钢筋应变等数据.数据采集系统采用MGCplus，通过Catman软件进行采集，采样频率为1 200 Hz.

图2 空载框架模型图

图3 均布荷载框架模型图

图4 框架锤击图

2 试验结果与分析

2.1 静力荷载-位移曲线

图5给出了框架中间柱头竖向荷载-位移曲线．由图5可知，试验框架在受力过程中经历了以下几个明显的阶段：AB段为弹性工作阶段，中间柱头竖向位移小于1.500 mm，框架梁上的裂缝在B点以后才出现.BC段为塑性受力阶段，在该阶段，随着荷载的增加，框架梁钢筋以及混凝土应变增加，当竖向位移达到17.530 mm时，边柱梁端出现塑性铰，到达C点时，达到最大承载能力14.837 kN.CD段为受压混凝土破坏阶段，从C点开始受压混凝土局部压碎，塑性铰区域混凝土严重剥落.D点(竖向位移215.640 mm)以后，边柱梁端一根受拉钢筋断裂，结构转化为悬索受力机制，主要由钢筋来承担荷载，达到E点时(竖向位移达到327.190 mm)，中柱梁端受拉钢筋断裂.中间柱头竖向位移达到462.330 mm时(F点)，框架梁达到悬索作用阶段的极限承载能力13.391 kN，其值小于C点对应的最大承载能力14.837 kN，表明对于钢筋混凝土平面框架，悬索效应阶段的极限承载能力小于塑性受力阶段的极限承载能力.试验破坏形态如图6所示.

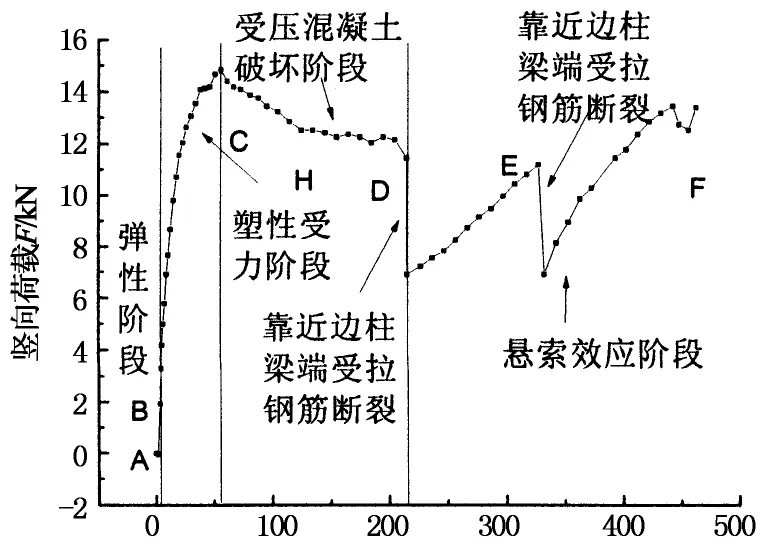
位移/mm

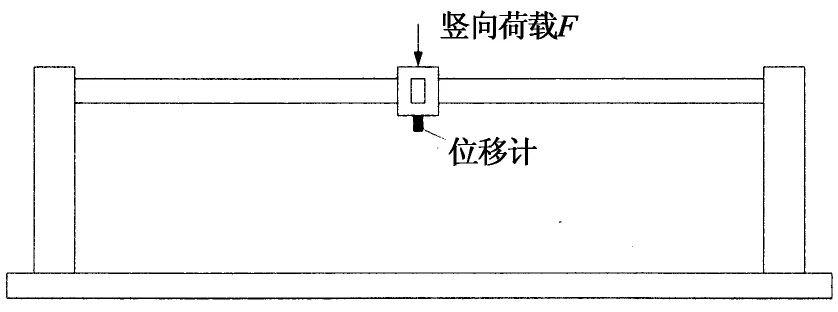
(b)加载示意图

2.2 动力试验结果与分析

2.2.1 中间柱头位移响应

锤击试验前，对试验框架结构进行了模态测试，测得空载框架的频率为14.623 0 Hz，阻尼比为0.043 1.锤击试验后，基于锤击试验中间柱头位移响应数据，获取了框架梁的振动信息，见表2和表3.部分位移响应时程曲线如图7所示，取移除千斤顶之前中间柱头位置为位移零点，曲线直线段表示框架梁在移除千斤顶过程中产生的竖向位移.

(a)整体破坏形态

(b)梁端局部破坏形态

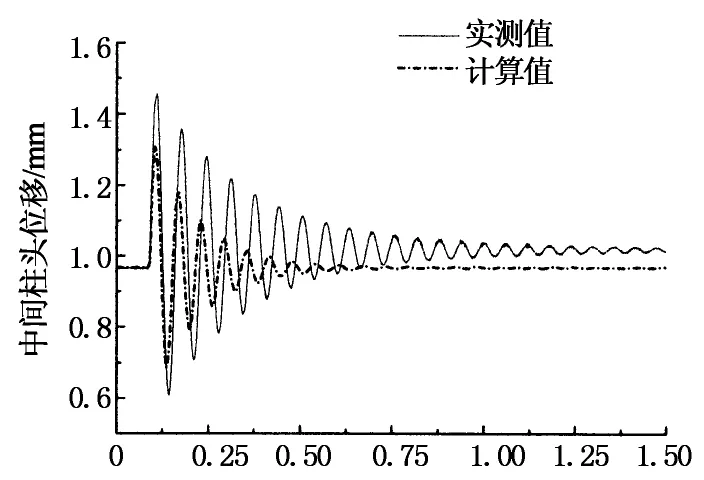
T/s(a)空载框架

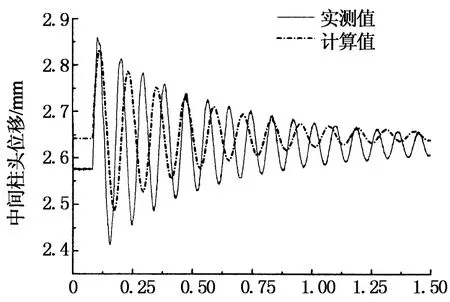
T/s(b)均布线荷载框架

图8给出了框架梁中间柱头竖向位移峰值与冲量的关系曲线，图中位移幅值以静平衡位置为零点.由图8可知，当框架梁处于弹性以及弹塑性受力阶段时，位移峰值与输入冲量近似呈线性关系，经过线性拟合得到如下简单的关系.空载情况：umax=0.047 74I；加载情况：umax=0.031 07I.

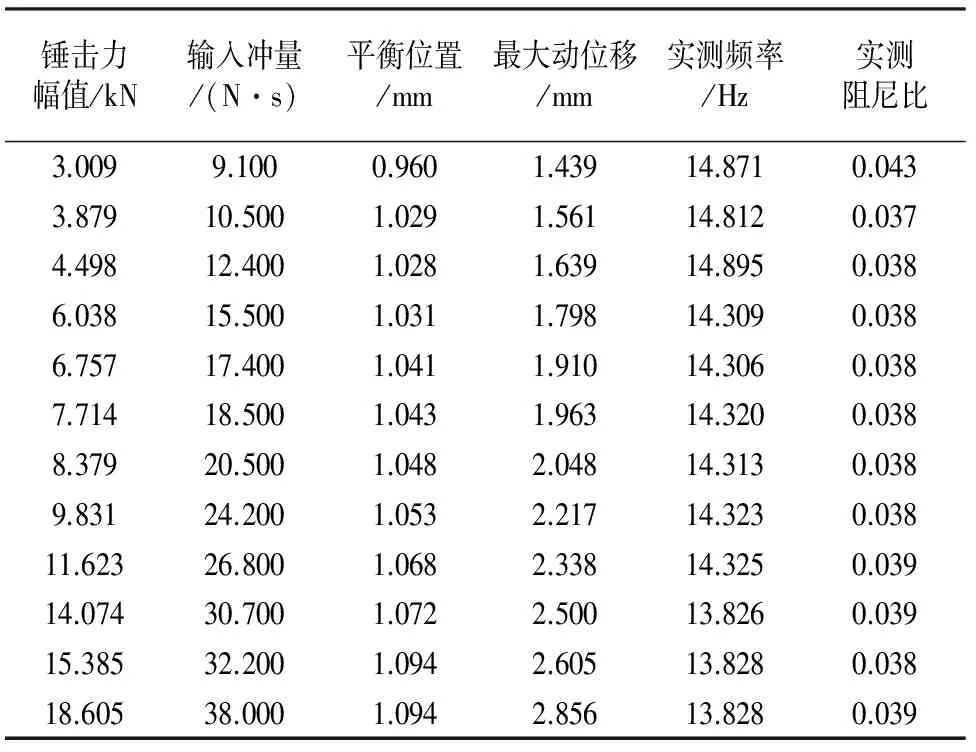
表2 空载框架梁振动特性

表3 均布线荷载框架梁振动特性

注：冲量大小即为锤击力时程曲线的面积，采用Matlab计算.

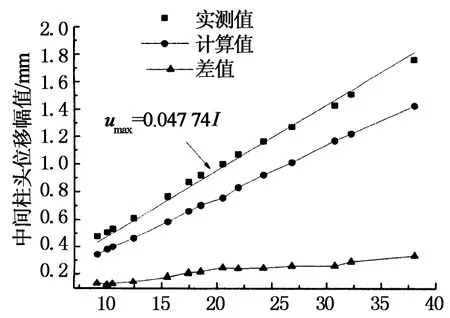
冲量/(N·s)(a)空载框架

冲量/(N·s)(b)均布线荷载框架

2.2.2 中间柱头加速度响应

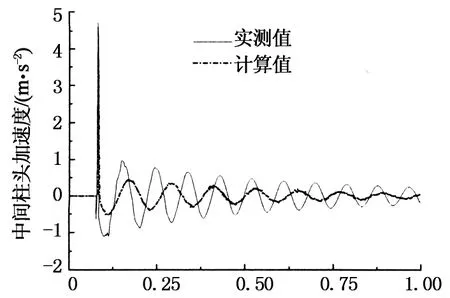
图9给出了加速度实测时程曲线．由图9可知，加速度曲线存在一个尖点，表明锤击瞬时，框架梁惯性力较大，而此时阻尼力和恢复力较小，主要由惯性力和锤击力形成动力平衡状态.通过以下比较分析能够进一步证实这一现象的存在．

对于空载框架，锤击力峰值为3.264 kN时，加速度峰值为 15.888 m/s2；对于均布线荷载框架，锤击力峰值为3.168 kN时，加速度峰值为4.717 m/s2, 15.888/4.717=3.368.理论上，均布线荷载框架的质量为空载框架的3.12倍，在同等当量锤击荷载作用下，其加速度幅值应该是空载框架的1/3左右，与实测结果吻合很好.

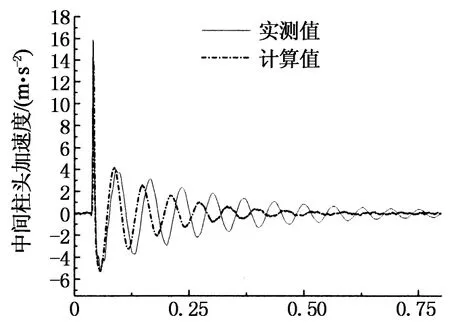
T/s(a)空载框架

T/s(b)均布线荷载框架

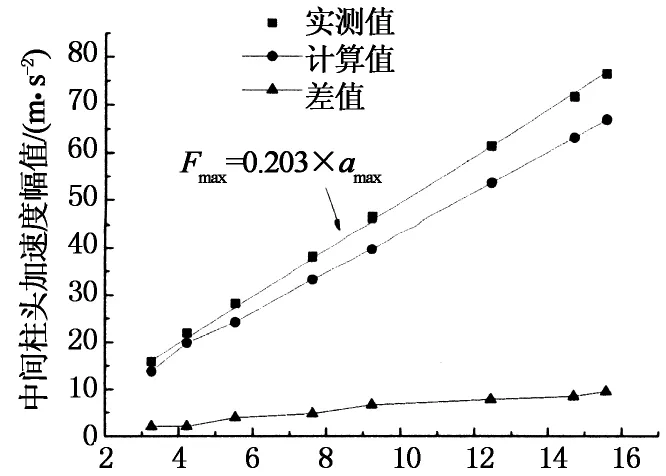
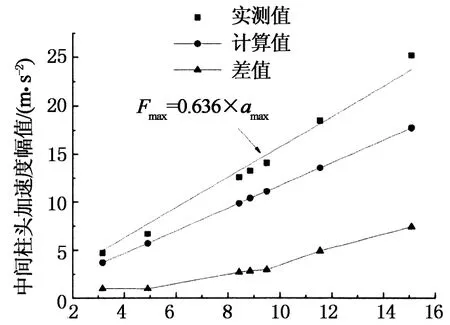
图10给出了加速度幅值与锤击力幅值的关系曲线．由上述分析可知，锤击力幅值和加速度幅值满足线性关系，经过线性拟合得到如下关系.空载情况：Fmax=0.203×amax；加载情况：Fmax=0.636×amax．

2.2.3 框架梁内力

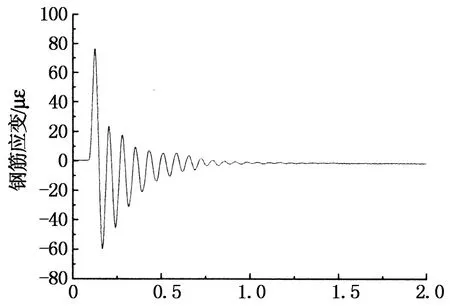
图11给出了锤击力峰值为14.074kN对应的空载框架梁钢筋应变时程曲线.由图11可知，梁钢筋应变表现出逐渐衰减的周期振动，梁两端钢筋拉应变很接近.在该级荷载作用下，边柱梁端上部混凝土开裂(混凝土开裂应变为140～280με左右[12])，中柱梁端混凝土没有开裂.表明此时框架梁处于弹塑性受力阶段，由于混凝土开裂，结构刚度有所下降，如表2所示.图12给出了锤击力峰值为4.908kN对应的均布线荷载框架梁钢筋应变时程曲线.由图12可知，梁钢筋应变表现出逐渐衰减的周期振动，在该级荷载作用下，中柱梁端混凝土开裂.

锤击力幅值/kN(a)空载框架

锤击力幅值/kN(b)均布线荷载框架

T/s(a)试验框架梁负弯矩处受拉端

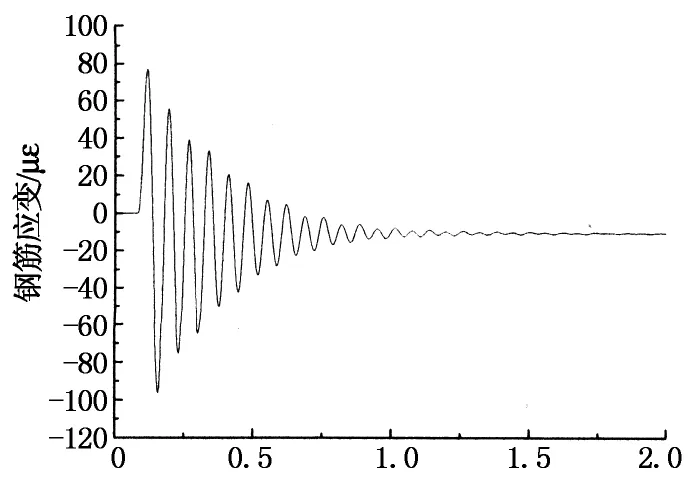
T/s(b)试验框架梁正弯矩处受拉端

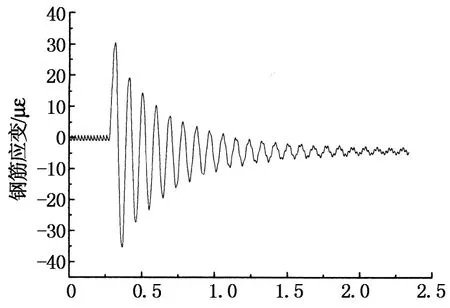
T/s(a)试验框架梁正弯矩处受拉端

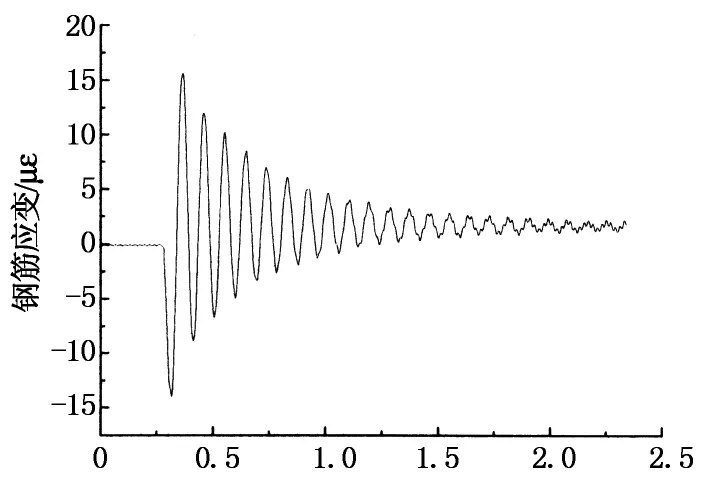
T/s(b)试验框架梁正弯矩处受压端

3 框架梁动力特性计算与倒塌分析

采用有限元软件SAP2000，以实测锤击力时程曲线为时程函数对试验框架进行动力时程分析，积分方法采用HHT方法，不考虑几何非线性和材料非线性，计算结果见图7～图10.由图7～图10可知，在弹性阶段，计算值与实测结果吻合较好.在弹塑性阶段，计算值与实测值存在一定的差别，主要原因是计算过程中没有考虑材料非线性和几何非线性.计算响应幅值与实测响应幅值满足相同的变化规律：位移幅值与输入冲量呈线性关系，加速度幅值与锤击力幅值呈线性关系.计算采用的阻尼比相对结构的实际阻尼比略大,故图7和图9中计算得到的曲线比实测曲线衰减显得略快.由于计算模型刚度与实测模型稍有差别，故导致图7所示位移曲线计算值与实测值略有偏差.

由文献[8]可知，竖向荷载作用下框架梁中柱梁端承受正弯矩，梁端截面开裂后中性轴上移，边柱梁端承受负弯矩，梁端截面开裂后中性轴下移.故在框架梁的两端，截面中性轴不在同一水平面上，框架梁形成“拱效应”.由图11和图12可知，空载框架边柱梁端混凝土开裂，中柱梁端没有开裂，框架梁拱效应现象不明显.在该阶段，由于混凝土的开裂，框架梁的频率下降，刚度降低.均布荷载框架梁两端混凝土均开裂，框架梁处于拱效应受力阶段.

由上述分析可知，拱效应形成之前，框架梁刚度随混凝土开裂而降低，拱效应形成之后，框架梁刚度有所提高.

由静载试验结果可知，框架梁的最大承载能力为14.837 kN，由表2 和表3可知，空载框架所受最大锤击力达到18.605 kN，均布线荷载框架所受最大锤击力达到15.083 kN，结构并没有倒塌.产生这一现象的主要原因解释如下：

根据文献[13]，冲击荷载作用下钢筋混凝土梁满足以下能量平衡方程：

方程右边为框架梁从位移原点到位移为u的过程中吸收的能量，可根据静力荷载-位移曲线求得.P0为上部等效冲击荷载；h为冲击高度；γ为冲击过程中的能量传递系数．假定冲击过程为完全塑性冲击，采用简化单自由度模型计算能量损失.

框架梁破坏准则定义如下：框架梁中间柱头竖向位移达到框架梁受力钢筋断裂对应的位移(图5中的D点)或框架梁中间柱头竖向位移大于其最大承载能力对应的位移(图5中的C点)且此位移对应的恢复力小于作用在框架梁上的等效冲击荷载P0时，框架梁将发生倒塌.对于图5中H点来说，如果R(H)小于等效冲击荷载，该框架将发生倒塌.采用上述分析方法和破坏准则对试验框架进行倒塌分析，试验框架发生倒塌时对应的冲击高度和质量如表4所示.

由表4可知，试验框架梁在冲击荷载作用下发生倒塌所需要的能量较大，而本次锤击试验采用的锤头质量只有6 kg，输入结构的冲击能量有限，不足以使其发生倒塌.

表4 倒塌分析结果

4 结 论

1)在弹性以及弹塑性受力阶段，框架梁动力位移幅值与输入冲量近似呈线性关系，锤击力幅值与加速度幅值近似呈线性关系，随着锤击力的增加，结构的阻尼变化较小，振动频率下降.

2)锤击荷载作用下，空载框架梁没有形成拱效应，其刚度随混凝土开裂而降低，均布线荷载框架梁形成拱效应，其刚度有所提高.空载框架梁和均布线荷载框架梁阻尼很接近，表明结构阻尼受其质量影响较小.

3)框架梁在静力受力过程中经历弹性阶段、塑性阶段、悬索效应阶段等三个明显的受力阶段.试验梁的最大承载能力为14.837 kN，出现在塑性受力阶段，悬索效应阶段的极限承载能力是13.397 kN，表明对于钢筋混凝土平面框架，悬索效应阶段的极限承载能力小于塑性受力阶段的极限承载能力.

4)静力试验结果表明，试验梁的最大承载能力为14.837 kN，其受到的最大锤击力达到18.605 kN，结构并未倒塌，主要是因力锤冲击能量不足以使结构发生倒塌，需通过增大力锤质量或锤击高度等方式获得足够的冲击能量以使其发生倒塌.

[1] MARJANISHVILI S, AGNEW E.Comparison of various procedures for progressive collpaseanalysis[J].Journal of Performance of Constructed Facilities, 2008, 20(4):365-375.

[2] NAJI A, IRANI F. Progressive collapse analysis of steel frames: Simplified procedure and explicit expression for dynamic increase factor[J]. International Journal of Steel Structures, 2012, 12(4): 537-549.

[3] KOKOT S, ANTHOINE A, NEGRO P,etal. Static and dynamic analysis of a reinforced concrete flat slab frame building for progressive collapse[J]. Engineering Structures, 2012, 40: 205-217.

[4] LIU M. A new dynamic increase factor for nonlinear static alternate path analysis of building frames against progressive collapse[J]. Engineering Structures, 2013, 48: 666-673.

[5] CHEN J, HUANG X, MA R,etal. Experimental study on the progressive collapse resistance of a two-story steel moment frame[J]. Journal of Performance of Constructed Facilities, 2011, 26(5): 567-575.

[6] QIAN K, LI B. Slab Effects on response of reinforced concrete substructures after loss of corner column[J]. ACI Structural Journal, 2012, 109(6):845-855.

[7] STINGER S M, ORTON S L. Experimental evaluation of disproportionate collapse resistance in reinforced concrete frames[J]. ACI Structural Journal, 2013, 110(3):521-529.

[8] 易伟建, 何庆锋, 肖岩. 钢筋混凝土框架结构抗倒塌性能的试验研究[J]. 建筑结构学报, 2007, 28(5): 104-109.

YI Wei-jian, HE Qing-feng, XIAO Yan. Collapse performance of RC frame structure[J]. Journal of Building Structures, 2007, 28(5):104-109.(In Chinese)

[9] DOD 2009．Design of buildings to resist progressive collapse[S].Washington DC: Department of Defense, 2010:21-62.

[10]GB 50010-2010 混凝土结构设计规范[S].北京：中国建筑工业出版社，2010: 34-130.

GB 50010-2010 Code for design of concrete structures [S]. Beijing: China Architecture & Building Press, 2010: 34-130. (In Chinese)

[11]GB 50011-2010 建筑抗震设计规范[S].北京：中国建筑工业出版社，2010: 31-65.

GB 50011-2010 Code for seismic design of building [S]. Beijing: China Architecture & Building Press, 2010: 31-65. (In Chinese)

[12]过镇海, 时旭东. 钢筋混凝土原理和分析[M]. 北京：清华大学出版社, 2003：29-30.

GUO Zhen-hai, SHI Xu-dong. Reinforced concrete theory and analyse[M]. Beijing:Tsinghua University Press, 2003: 29-30. (In Chinese)

[13]VLASSIS A G, IZZUDDIN B A, ELGHAZOULI A Y,etal. Progressive collapse of multi-storey buildings due to failed floor impact[J]. Engineering Structures, 2009, 31(7): 1522-1534.

Experimental Study of the Collapse Performance of RC Frame under Hammer Load

HE Qing-feng†, LIU Yi-ren, JIANG Qu-chong, YI Wei-jian

(College of Civil Engineering，Hunan Univ, Changsha, Hunan 410082,China)

Two 2-bay, 1-story RC plane frames were tested to study the static and dynamic behavior of RC frame structure after the column's failure. A static experiment was done to obtain the static behavior data of frame structure, and based on another test frame, hammer experiments were used to obtain the frame beam's dynamic response data of displacement, acceleration and steel strain under no load and uniformly distributed load, respectively. The mechanic behavior of the frame beam under hammer load was studied by comparing the static and dynamic test results. The tests results were as follows: there was a linear relationship between the dynamic displacement amplitude and the input impulse under hammer load; with the increase of the hammer load, the damping of the structure changed little while the frequency decreased; the frame beam with uniformly distributed load formed the arch effect under hammer load, so its stiffness increased slightly; the maximum hammer load exceeded the frame beam's maximum resistance force, but the frame beam did not collapse because of the small impact energy.

reinforced concrete frames; hammering method; dynamic effect; progressive collapse

1674-2974(2015)01-0040-07

2014-02-02

国家自然科学基金资助项目(51108170,51408213)， National Natural Science Foundation of China(51108170,51408213)

何庆锋(1979-)，男，湖北黄冈人，湖南大学讲师，博士†通讯联系人，E-mail:l5672101@qq.com

TU375.1;TU375.4

A