有腹筋预应力超高强混凝土梁受剪承载力试验研究

姚大立，贾金青，余 芳

(1．大连理工大学 港口和近海工程国家重点实验室，辽宁 大连 116024；2．沈阳工业大学 建筑工程学院，辽宁 沈阳 110178)

有腹筋预应力超高强混凝土梁受剪承载力试验研究

姚大立1,2，贾金青1†，余 芳2

(1．大连理工大学 港口和近海工程国家重点实验室，辽宁 大连 116024；2．沈阳工业大学 建筑工程学院，辽宁 沈阳 110178)

为揭示有腹筋预应力超高强混凝土梁受剪性能，通过11根预应力超高强混凝土梁和4根预应力普通混凝土梁受剪性能试验，对比分析了不同参数对试验梁的破坏形态、荷载-挠度曲线、承载能力和钢筋应变的影响.结果表明：预应力超高强混凝土梁的破坏形态与预应力普通混凝土梁相似，且预应力超高强混凝土梁具有更好的刚度、承载能力和剪切延性.增大剪跨比和箍筋间距均可降低极限承载力，另外，当预应力度大于0.34时，提高预应力度对极限承载力才有积极贡献.建立了有腹筋预应力超高强混凝土梁斜截面受剪承载力的计算公式，计算结果与试验结果吻合较好.此外，利用现行规范(GB 50010-2010)计算有腹筋预应力超高强混凝土梁受剪承载力的计算结果离散性较大，计算结果不稳定.

剪跨比；预应力；受剪承载力；破坏形态

随着桥梁工程技术的不断发展，大跨度、高强装配式后张法预应力混凝土桥梁被广泛应用于公路工程建设项目中[1-2]，高强高性能混凝土作为一种新型混凝土，其在强度、耐久性、工作性能及体积稳定性等方面均优于普通混凝土，但同时也存在脆性大、延性差等弱点.现有规范适用的混凝土强度等级为C15～C80，然而随着混凝土技术的发展，比文献[3]混凝土强度等级更高的超高强混凝土在实际工程中也得到广泛应用.目前，国内智菲[4]等已对8根预应力高强混凝土(C70)梁的抗剪强度进行了试验研究，观察了裂缝开裂特点和破坏形态，并给出受剪承载力建议性公式.Graybeal对预应力超高强混凝土梁的弯曲性能进行了试验研究[5].但是，目前尚无学者对预应力超高强混凝土(C100)梁的剪切性能进行理论或试验方面的研究，使得相关理论和研究成果严重滞后于工程实践.

本文通过有腹筋预应力超高强混凝土简支梁受剪试验，揭示了梁的受剪机理，系统研究了影响试验梁受剪性能的主要因素，并结合我国现行《混凝土结构设计规范》(GB 50010—2010)和《高强混凝土结构技术规程》(CECS 104—99)，提出了有腹筋预应力超高强混凝土梁斜截面受剪承载力计算公式.

1 试验概况

共设计了11根有腹筋预应力超高强混凝土和4根预应力普通混凝土简支梁，截面尺寸为160 mm×340 mm.试验梁长为1 200 mm, 1 400 mm, 1 600 mm，其中剪跨区段长为840 mm, 1 120 mm, 1 400 mm，分别对应的剪跨比为1.5, 2.0和2.5.试件的混凝土强度设计等级分别为C40, C70和C100，试验梁的受拉钢筋为3根直径20 mm的HRB335级钢筋，屈服强度为370 N/mm2，箍筋为直径6.5 mm的HPB235级钢筋，屈服强度为335 N/mm2，预应力筋采用1860级钢绞线，张拉控制应力为σcon=0.75fptk(fptk为抗拉强度标准值)，直径分别为15.2 mm和12.7 mm，屈服强度分别为1 815 N/mm2和1 798 N/mm2，采用有黏结预应力工艺.为降低张拉阶段的预应力损失，本次试验采用低回缩预应力锚具，主要试验变量为剪跨比λ, 箍筋间距s, 混凝土强度fcu和预应力度λp.根据文献[6]，预应力度λp定义为式(1).试验梁参数和主要试验结果列于表1，混凝土材料力学性能见表2.

λp=(Apsfps)/(Apsfps+Asfy).

(1)

式中：Aps为预应力钢筋总面积;As为纵向受拉钢筋总面积;fps为预应力筋的屈服强度;fy为纵向受拉钢筋的屈服强度.

表1 试验梁参数和试验结果汇总

表2 混凝土力学性能

2 测点布置及加载方案

在加载点和支座范围的箍筋上均粘贴有电阻应变片，梁跨中的受拉钢筋和预应力筋表面粘贴电阻应变片.将LVDT置于梁跨中底部和支座处，以测得梁的整体变形.采用单调静力加载制度，正式加载时，每级荷载约为预估极限荷载的10%，每加一级荷载，持载10 min.接近预估开裂荷载时，适当降低每级荷载增量以期较准确地获取实际开裂荷载.加载至极限荷载85%时则以位移控制加载，加载速率为0.02 mm/min.所有试验数据均通过IMC数据采集仪全自动采集.试验测试内容：试件开裂荷载、极限荷载；钢筋及混凝土应变；荷载-挠度曲线及裂缝开展情况等.试验装置及混凝土测点布置见图1，典型试件的应变片布置见图2.

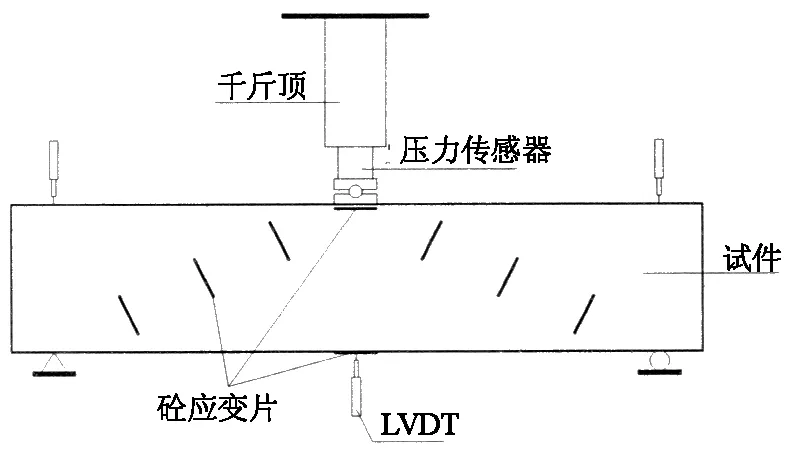
图1 试验装置及测点布置图

图2 部分试件的应变片布置图

3 主要试验结果与分析

3.1 破坏形态

预应力超高强混凝土梁破坏形态与预应力普通混凝土梁基本相似.加载初期，试验梁处于弹性阶段，加载至极限荷载的17%～32%时，梁跨中加载点的正下方出现竖向裂缝，随着荷载的增大，在剪跨区内也出现高度略低于受拉钢筋中心的竖向裂缝，且斜向加载点方向发展.当加载到极限荷载的36%～53%时，剪跨区内预应力钢筋位置处出现斜裂缝，且斜裂缝出现很突然，荷载继续增加，竖向裂缝发展缓慢，斜裂缝宽度加大.当荷载接近试验梁斜截面的极限承载力时，试验梁挠度增长加快，斜裂缝向上延伸至集中荷载作用点处，向下延伸至受拉钢筋位置，并沿着受拉钢筋向支座发展.此时荷载已达到试验梁的斜截面承载能力.预应力超高强混凝土梁的斜裂缝面较普通强度混凝土梁光滑平整，破坏面沿裂缝的粗骨料大部分被劈开，这表明与普通强度混凝土相比，超高强混凝土骨料咬合作用有所降低.在试验加载的过程中，所有的试验梁都是箍筋首先屈服，受拉钢筋未屈服而发生剪压破坏.预应力超高强混凝土梁的开裂荷载和极限荷载见表1，破坏形态如图3所示.

图3 试验梁的破坏形态

3.2 荷载-挠度曲线分析

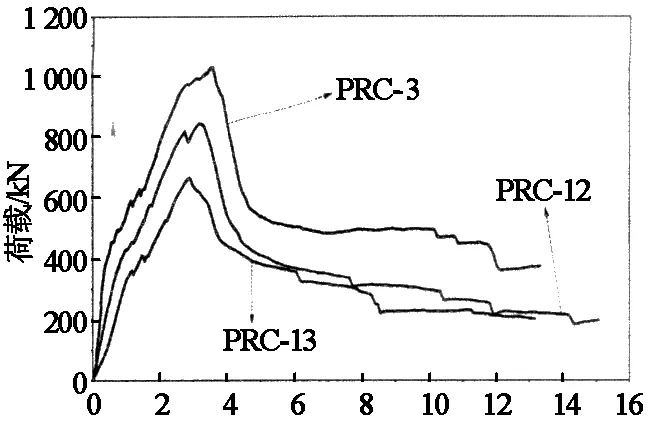
图4给出了试验梁的荷载-挠度曲线.

从图4中可看出预应力超高强混凝土梁的受力大致可分为3个阶段：1)从开始加载至试验梁斜截面开裂属于弹性阶段.在此阶段，试验梁表现出整体工作性能，荷载-挠度曲线呈线性; 2)弹塑性阶段.从斜截面开裂至极限承载力为弹塑性阶段.在此阶

挠度/mm

挠度/mm

挠度/mm

挠度/mm

段，挠度发展显著加快，试验梁的荷载-挠度曲线呈非线性，刚度明显降低.3)破坏阶段.从极限承载力至卸载阶段为试验梁的破坏阶段.图4(a)示出了剪跨比对试验梁荷载-挠度曲线的影响.由图可见：预应力超高强混凝土梁的斜裂缝出现后，试验梁的刚度随剪跨比增加而逐渐减小，因为剪跨比λ=M/V反映了试验梁破坏截面的弯矩与剪力的相对比值，在剪力水平相同的情况下，对于剪跨比较大的试验梁，斜裂缝形成后的截面有效惯性矩减小，因此导致试验梁的刚度显著降低.图4(b)示出了不同预应力度对试验梁荷载-挠度曲线的比较.由图可见：预应力度增加，荷载-挠度曲线的上升段斜率增大.这是由于增大预应力度提高了试验梁的刚度.图4(c) 示出了混凝土强度对荷载-挠度曲线的影响，由图可见：试验梁的初始刚度随着混凝土强度的增加而增大，这是因为混凝土弹性模量随着抗压强度的提高而增大.然而，混凝土抗压强度的增加并没有致使试验梁的剪切延性降低，反而增大.根据剪切延性系数的计算理论[7]，试验梁PRC-3的剪切延性系数为1.73，而试验梁PRC-13的剪切延性系数为1.36，同理，试验梁PRC-07和PRC-15的剪切延性系数分别为2.12和1.52.这是由于超高强混凝土与普通强度混凝土相比具有更小的水灰比，因此钢筋与超高强混凝土间具有更大的黏结力，从而导致预应力超高强混凝土梁具有更好的变形能力.图4(d)表明了箍筋间距只影响试验梁的斜截面承载力，对试验梁的刚度无作用.

3.3 荷载-应变曲线分析

3.3.1 荷载-箍筋应变曲线

图5给出了部分试件的荷载-箍筋应变曲线，相应的箍筋应变片布置见图1.可以看出：预应力超高强混凝土梁与预应力普通混凝土梁相似，在斜向裂缝出现瞬间，荷载-箍筋应变曲线出现突变点.斜裂缝出现前，箍筋应变很小，以梁PRC-10和PRC-14为例，当荷载达到梁的斜截面开裂荷载时，箍筋应变值分别为9.81 με和61.03 με.由此看出，箍筋对试验梁的斜截面开裂荷载几乎没有任何作用.这是因为箍筋直径较小且表面光滑.因此，斜裂缝形成以前，箍筋对混凝土的约束能力不显著.

箍筋应变/με

箍筋应变/με

3.3.2 荷载-纵筋应变曲线

为使试件发生剪切破坏，本次试验的所有试验梁纵筋配筋率较大，从试验结果看，最终破坏时全部试件的受拉钢筋均未屈服.图6给出了部分试件的荷载-受拉钢筋应变曲线.可以看出：随着荷载的增加，仅在弯曲裂缝出现瞬间，荷载-受拉钢筋应变曲线出现1次突变.而主斜裂缝是从梁腹分别向加载点和支座方向发展，斜截面开裂瞬间，斜裂缝还没有到达受拉钢筋截面处，因此，无法从荷载-受拉钢筋应变曲线观测到斜向裂缝出现点.

受拉钢筋应变/με

受拉钢筋应变/με

3.3.3 荷载-预应力筋应变曲线

图7给出了荷载-预应力筋应变曲线.可以看出：预应力超高强混凝土梁的荷载-预应力筋应变发展规律与预应力普通混凝土梁相似.在整个加载过程中，试验梁弯曲裂缝和斜向裂缝出现的2个时刻，荷载-预应力筋应变曲线出现了2次比较明显的突变.最后，随着荷载的增加，预应力筋应变随之增大，直至应变片脱落或拉断.

3.4 承载能力影响因素分析

3.4.1 不同剪跨比影响

剪跨比是影响预应力超高强混凝土梁受剪承载能力的主要因素.由图8(a)试验梁的荷载-剪跨比的关系曲线可以看出：随着剪跨比的增大，试验梁的极限荷载减小.剪跨比较小时，剪跨比与极限荷载的关系曲线较陡，随着剪跨比的增大，曲线趋向平缓.这是由于在支座和集中荷载作用处产生竖向压应力σy，σy的存在减小了混凝土的主拉应力值，提高了极限承载能力.当剪跨比较小时，剪跨区段较短，σy在整个剪跨区的作用较为明显；当剪跨比较大时，剪跨区段较长，而σy的影响只存在于支座及集中荷载附近，所以，σy在整个剪跨区段的作用较弱.

预应力筋应变/με

预应力筋应变/με

3.4.2 不同箍筋间距影响

箍筋间距是影响预应力超高强混凝土梁受剪承载能力的另一个重要因素，从图8(b)试验梁的荷载-箍筋间距的曲线可以看出：试验梁的极限荷载随着箍筋间距的减小而增大.但是对于剪跨比不同的试验梁，极限荷载随着箍筋间距减小而增大的程度并不相同，剪跨比为1.5时的极限荷载随箍筋间距减小而增大的趋势较剪跨比为2.0时更明显.

3.4.3 不同混凝土强度影响

预应力超高强混凝土梁的斜截面剪切破坏是由于混凝土达到相应受力状态下的极限强度而发生的，故混凝土强度对斜截面的承载能力影响很大.由图8(c)试验梁的荷载-混凝土强度的关系曲线可以看出：其他条件均相同，仅混凝土强度不同的情况下，试验梁的极限荷载随着混凝土强度的提高而增大，并且这种趋势随着剪跨比的增加而逐渐减弱.

3.4.4 不同预应力度影响

增大预应力度不仅可以提高试验梁的刚度，减小破坏时的变形，而且也可以显著提高试验梁的斜截面承载能力，因为增大预应力度可以提高骨料的咬合作用，从而对斜裂缝的产生和开展具有一定的抑制作用.同时，增大预应力度也可以增大试验梁的剪压区高度.但是从图8(d)试验梁的荷载-预应力度的关系曲线可以看出：当预应力度λp≤0.34时，预应力度的增加对试件的承载能力几乎没有作用；当λp>0.34时，极限荷载随着预应力度增加而显著增大.这可能因为预应力度取值过小会导致试验梁截面的有效预压应力过小，进而预应力对试验梁斜截面承载能力的积极作用减弱.

λ(a)

s/mm(b)

fcu/MPa(c)

λp(d)

4 受剪承载力分析

依据预应力混凝土梁受剪机理[8]可知：当混凝土梁施加预应力后，其内部的应力状态将发生改变，斜裂缝与试验梁轴线的夹角减小，剪压区高度增大，另外预应力能有效阻止斜裂缝的开展，增强斜裂缝面上骨料咬合力，从而提高试验梁的受剪承载力.根据前面的试验结果可以发现，当剪跨比改变时，预应力度对受剪承载力的影响程度也随之发生变化.根据文献[9]，建议预应力提供的受剪承载力Vp如式(2)所示，其中Np0为计算截面上混凝土法向预应力等于零时的纵向预应力钢筋及非预应力钢筋的合力，采用试验方法求得，计算结果如表3所示，其实测数据和计算方法见文献[10]和[11].

(2)

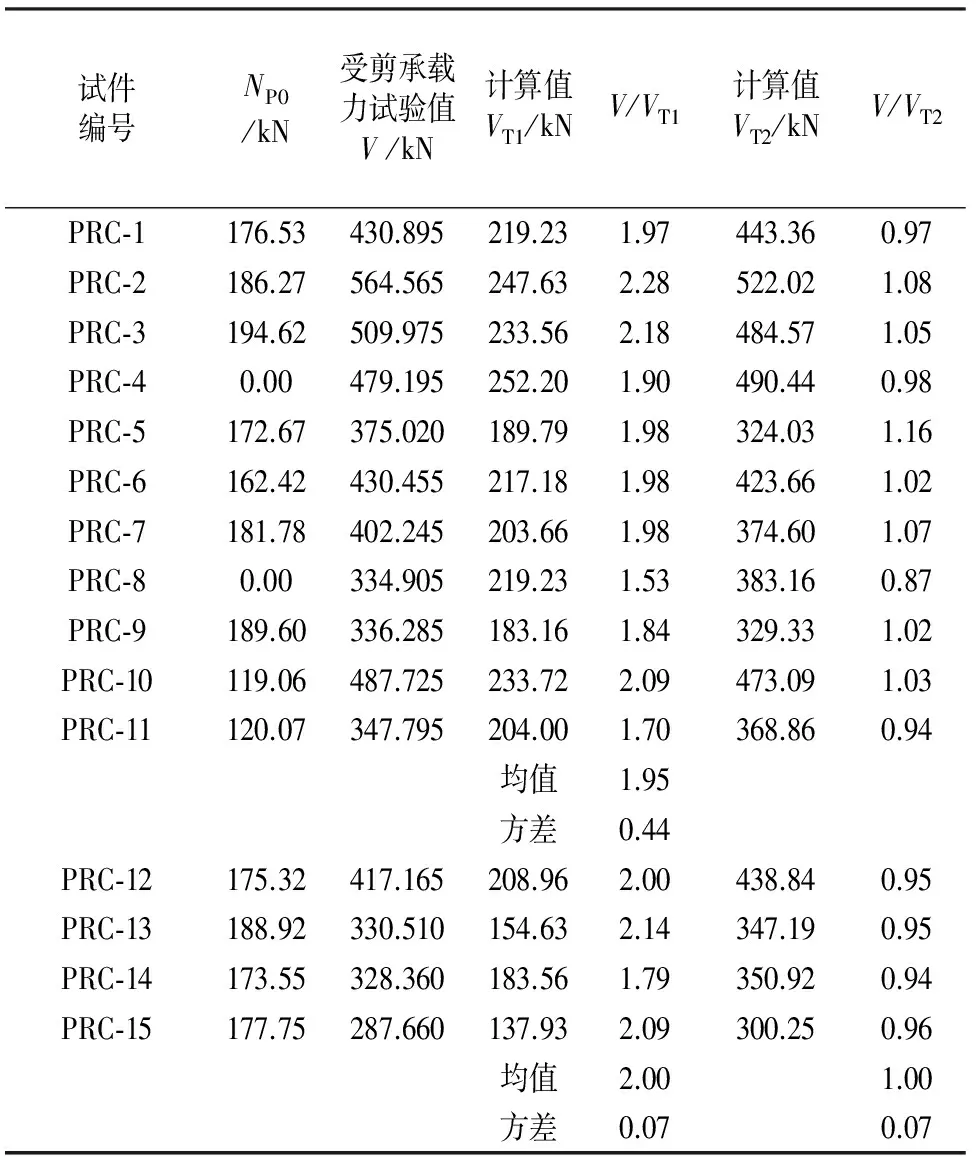
表3 受剪承载力计算结果

注：V为受剪承载力试验值；VT1为参照规范GB 50010—2010计算的受剪承载力；VT2为参照本文提出的式(6)计算的受剪承载力.

试验研究表明：箍筋对受剪承载力的贡献主要靠本身所能承担的剪力和提高斜裂缝间的咬合及纵筋的销栓作用，且随着箍筋间距s的减小，这些作用越明显.根据文献[12]和[13]可知，在s一定，且剪跨比1.0≤λ≤3.0时，箍筋对试验梁的受剪强度随

剪跨比的增大而增强.且箍筋的受剪强度与剪跨比成正比关系，根据上述分析，建议Vs如式(3)所示：

(3)

通过文献[14]中的关于高强高性能混凝土力学性能试验研究的相关测试数据可以看出：混凝土强度等级的提高，其抗压强度的提高远远高于混凝土抗拉强度的提高，对于超高强混凝土，该现象将更为突出，鉴于材料的破坏由较低指标来控制，并且参考文献[11]，本文仍用混凝土抗拉强度ft作为控制指标.因此，建议Vc如式(4)所示：

Vc=αftbh0.

(4)

根据以上分析，则预应力超高强混凝土梁斜截面受剪承载力的计算通式可表达如式(5).

(5)

式中：α,β和γ分别为混凝土、箍筋和预应力筋项的抗力系数.

根据本文所完成的15根试验梁受剪试验的测试数据，如表1所示，拟合出各项抗力系数，并将拟合结果代入式(5)，即得有腹筋预应力超高强混凝土梁斜截面受剪承载力的计算公式：

(6)

式中：剪跨比λ<1.0时，取λ=1.0，剪跨比λ>3.0时，取λ=3.0.

参照规范和式(6)对表1中的15根试验梁受剪承载力进行计算，并与实测值进行比较分析，计算结果见表3.分析表3可以得出：

1)有腹筋预应力超高强混凝土梁试验值与文献[11]中的公式计算值相比较，均值为1.95，方差为0.44；将本试验中预应力普通混凝土梁和文献[15]中10根试验梁的试验值与文献[11]中的公式计算值相比较，均值分别为2.00和1.92，方差为0.07和0.05，由此看出：文献[11]公式计算有腹筋预应力超高强混凝土梁与计算预应力普通混凝土梁具有同样的安全性，剪跨比越小，安全程度越大，剪跨比相同时，随着预应力度的提高，试验值与计算值的比值越大.对比分析方差可以得出：利用文献[11]中的公式计算预应力普通混凝土梁(混凝土强度等级为C40～70)的受剪承载力的计算结果离散性较小，计算结果可靠，但是计算有腹筋预应力超高强混凝土梁时离散性较大，计算结果不稳定．

2)本文提出的有腹筋预应力超高强混凝土梁受剪承载力计算公式的计算结果与试验结果吻合较好，能够客观地反映预应力超高强混凝土梁的受剪性能.

5 结 论

1) 预应力超高强混凝土梁的破坏形态与预应力普通混凝土梁相似，均为初裂、裂缝开展和破坏3个阶段，在剪跨比1.5≤λ≤2.5时，破坏形态均为剪压破坏.

2) 极限承载力随着剪跨比和箍筋间距的增大而降低，提高混凝土强度，试验梁的剪切延性和极限承载力均有提高.当预应力度λp≤0.34时，预应力度对试验梁的极限承载力几乎无影响，当λp>0.34时，极限承载力随预应力度的增加而增大.

3) 建立了预应力超高强混凝土梁受剪承载力简化计算公式.计算结果与试验结果对比分析表明，本文提出的计算公式具有较高的精度，可供进一步研究参考.利用现行规范(GB 50010—2010)计算有腹筋预应力超高强混凝土梁受剪承载力的计算结果离散性较大，计算结果不稳定.

[1] 郑辉，方志，曹敏辉. 配置竖向预应力筋混凝土箱梁抗剪性能试验[J]. 湖南大学学报:自然科学版，2013，40(1)：1-8.

ZHENG Hui, FANG Zhi, CAO Min-hui. Experimental study on the shear behavior of reinforced thin-wall box girders with vertical prestressed tendon [J]. Journal of Hunan University : Natural Sciences, 2013, 40(1): 1-8. (In Chinese)

[2] 周亚栋，邵旭东，刘海波. 预应力混凝土低高度梁桥结构形式比较研究[J]. 湖南大学学报:自然科学版，2010，37(8)：6-11.

ZHOU Ya-dong, SHAO Xu-dong, LIU Hai-bo. Comparative study of the structural types of prestressed concrete low-height beam bridge [J]. Journal of Hunan University: Natural Sciences, 2010, 37(8): 6-11. (In Chinese)

[3] JTG D 62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. 北京：人民交通出版社，2004：10-11.

JTG D 62—1004 Code for design of highway reinforced concrete and prestressed concrete bridges and culverts [S]. Beijing: China Communications Press, 2004: 10-11. (In Chinese)

[4] 智菲，叶知满. 预应力高强混凝土有腹筋T 形截面梁抗剪承载力试验研究[J]. 工业建筑，2007，37(S):321-413.

ZHI Fei, YE Zhi-man. Supported and prestressed high-strength concrete beam (T-section) with web reinforcement [J].Industrial Construction, 2007, 37(S): 321-413. (In Chinese)

[5] GRAYBEAL B A. Flexural behavior of an ultrahigh-performance concrete I-girder [J]. Journal of Bridge Engineering, 2008, 13(6): 602-610.

[6] SHAHAWI M E, BATCHELOR B V. Fatigue of partially prestressed concrete [J]. Journal of Structure Engineering, 1986, 112(3): 524-537.

[7] 张宏战，黄承逵. 钢筋钢纤维高强混凝土箍筋梁剪切延性分析[J]. 大连理工大学学报，2005，45(3): 422-426.

ZHANG Hong-zhan, HUANG Cheng-kui. Study of ductility of steel fiber reinforced high-strength concrete beams with stirrups [J]. Journal of Dalian University of Technology, 2005, 45(3): 422-426. (In Chinese)

[8] 陈彬. 预应力PRC梁抗剪性能研究[D]. 长沙：湖南大学土木工程学院, 2007：39-43.

CHEN Bin. Study on the shear strength of prestressed PRC girders [D]. Changsha: College of Civil Engineering, Hunan University, 2007: 39-43. (In Chinese)

[9] 杜修力，王作虎，詹界东，等. 预应力CFRP筋混凝土梁受剪性能试验研究[J]. 建筑结构学报，2011，34(4): 80-86.

DU Xiu-li, WANG Zuo-hu, ZHAN Jie-dong,etal. Experimental studies on shear behavior of concrete beams prestressed with CFRP tendons [J]. Journal of Building Structures, 2011, 34(4): 80-86. (In Chinese)

[10]姚大立，贾金青，涂兵雄，等. 预应力超高强混凝土弹性刚度分析[J]. 武汉理工大学学报: 交通科学与工程版, 2013，37(1): 74-76.

YAO Da-li, JIA Jin-qing, TU Bing-xiong,etal. Elastic stiffness analysis on ultra-high strength prestressed concrete beam [J]. Journal of Wuhan University of Technology: Transportation Science & Engineering, 2013, 37(1): 74-76. (In Chinese)

[11]GB 50010—2010 混凝土结构设计规范[S]. 北京：中国建筑工业出版社，2010：142-145.

GB 50010—2010 Code for design of concrete structures [S]. Beijing: China Architecture & Building Press, 2010: 142-145. (In Chinese)

[12]江炳章. 预应力度及剪跨比对部分预应力混凝土梁抗剪强度的影响[J]. 广西大学学报: 自然科学版，1988 (1): 30-38.

JIANG Bing-zhang. Effection on shear strength of partial prestressed concrete beams due to the degree of prestress and the shear span-depth ratio [J]. Journal of Guangxi University:Natural Science, 1988(1): 30-38. (In Chinese)

[13]郑升宝. 横张预应力混凝土梁抗剪性能的试验究[D]. 重庆：重庆交通学院, 2003：47-49.

ZHENG Sheng-bao. Experimental study on shear behavior of vertically tensioned prestressed concrete beams [D]. Chongqing: Chongqing Jiaotong Institute, 2003: 47-49. (In Chinese)

[14]蒲心诚，王志军，王冲，等. 超高强高性能混凝土的力学性能研究[J]. 建筑结构学报，2002，23(6)：49-55.

PU Xin-cheng, WANG Zhi-jun, WANG Chong,etal. Mechanical properties of super high-strength and high performance concrete [J]. Journal of Building Structures, 2002, 23(6): 49-55. (In Chinese)

[15]吕志涛.预应力混凝土受剪承载力计算[M]//钢筋混凝土结构研究报告选集(2). 北京：中国建筑工业出版社，1981：73-78.

LV Zhi-tao. Shear strength calculation of prestressed concrete beam[M]//Reinforced Concrete Structure Research Report Anthology (2). Beijing: China Building Industry Press, 1981: 73-78.(In Chinese)

Experimental Study of the Shear Capacity of Prestressed Ultra-high Reinforced Concrete Beams with Stirrups

YAO Da-li1, 2, JIA Jin-qing1†, YU Fang2

(1．State Key Laboratory of Coastal and Offshore Engineering, Dalian Univ of Technology, Dalian, Liaoning 116024, China;2．School of Architecture and Civil Engineering, Shenyang Univ of Technology, Shenyang, Liaoning 110178, China)

In order to investigate the shear behavior of prestressed ultra-high reinforced concrete beams, a total of 11 prestressed ultra-high reinforced concrete beams and 4 prestressed ordinary reinforced concrete beams were tested. The experimental study addressed failure mode, load-delfection curve, ultimate load capacity and the steel strain. The test results have shown that failure mode of prestressed ultra-high reinforced concrete beams is similar with that of prestressed ordinary reinforced concrete beams. Generally, prestressed ultra-high reinforced concrete beams have better higher stiffness and ultimate load capacity, as well as shear ductility. An increase in the shear span-depth ratio or space of stirrups decreases ultimate load capacity. In addition, it has positive effect on the ultimate load capacity for degree of prestress of more than approximately 0.34. A calculating formula for shear capacity of prestressed ultra-high reinforced concrete beams with stirrups was offered. The calculation results agree well with the test conclusions. The current China code (GB 50010-2010) used for the design of prestressed ultra-high reinforced concrete beams is very unstable and the dispersion ratio is high.

shear span-depth ratio; prestressing; shear capacity; failure model

1674-2974(2015)03-0023-08

2013-08-21

国家自然科学基金资助项目(51078059),National Natural Science Foundation of China(51078059); 辽宁省教育厅科学技术研究项目(L2014043)；科技部“863”计划重大交通基础设施核心技术项目(2007AA11Z133)

姚大立(1982-)，男，辽宁铁岭人，大连理工大学博士研究生，沈阳工业大学讲师

†通讯联系人，E-mail: keyknown@163.net

TU378．8

A