基于一种新型磁场-电路耦合法的多绕组变压器复合短路阻抗及短路环流计算

罗隆福，廖闻迪，许加柱，卢 赛

(湖南大学 电气与信息工程学院，湖南 长沙 410082)

基于一种新型磁场-电路耦合法的多绕组变压器复合短路阻抗及短路环流计算

罗隆福，廖闻迪†，许加柱，卢 赛

(湖南大学 电气与信息工程学院，湖南 长沙 410082)

多绕组变压器在不同短路工况下存在不同的短路阻抗，称为复合短路阻抗；不同短路工况下的各绕组电流均不相同.针对复合短路阻抗与短路环流存在的计算困难和计算时间长等问题，给出一种基于新型磁场-电路耦合方法的多绕组变压器复合短路阻抗及短路环流计算方法.在建立简化变压器磁场模型，得到绕组的电感矩阵后，将电感矩阵与外围电路结合，可以很快得到多绕组变压器复合短路阻抗与相应的短路环流.以某8绕组变压器为例验证，实测值表明该计算方法计算精度高，耗时较少，具有良好的工程应用价值.

新型磁场-电路耦合法；复合短路阻抗；短路环流；多绕组变压器

多绕组变压器以其节省成本，减小占地面积，可提供多幅值电压的优势，在电力系统，机车牵引供电，交直流电能变换领域中得到了广泛的应用[1-5].由于其多绕组，大容量，多电气端口的特点，多绕组变压器的短路阻抗尤其是多对一、多对多绕组短路情况下的复合短路阻抗计算，一直是变压器设计制造的关键问题之一；而多绕组变压器在不同短路工况下的短路环流，直接影响变压器绝缘参数设计.

多绕组变压器复合短路阻抗与环流计算已存在几种类型的计算方法，但也存在各自的优缺点.

复合短路阻抗计算：①直接计算法.文献[6]提出采用漏磁路计算的方法，对某一种多绕组变压器短路阻抗进行计算，但其针对范围过于狭窄，不能满足对多种多绕组变压器短路阻抗计算的广泛通用性.②能量法.文献[7]首先提出用功率法求解多绕组变压器建立磁场所需要的无功功率，而无功功率的最大值即为变压器磁场能量幅值.文献[8]根据磁场能量计算了多绕组变压器两两绕组短路时的短路阻抗，进一步利用矩阵变换来计算变压器复合短路阻抗，是一种实用可行的算法.但这种计算方法求解多个单对单绕组的短路阻抗，就需要在有限元软件中进行多次计算；通过矩阵变换来计算复合短路阻抗，对于不同变压器需要具体情况具体解，增加了求解的难度.③磁场电路耦合法.文献[9-12]提出利用场路耦合法计算变压器短路阻抗，计算方法为：首先建立多绕组变压器的有限元磁场模型，再在磁场模型外建立电路模型，根据不同的短路工况，求解复合短路阻抗与短路环流.这种方法在建立变压器模型阶段，需要输入铁心饱和曲线，并且由于变压器铁心B-H曲线的非线性，使得单次场路计算时间很长；需要每次设定不同的短路工况，来求解某一绕组或某些绕组的复合短路阻抗，总体的工作量与工作时间很长.

多绕组变压器的短路环流测量目前存在的问题为：工程上往往采用所有高压绕组并联浇注制成，供高压绕组实验测量的端口仅为所有高压绕组的并联端，因此无法单独测量某个高压绕组上的电流大小与电流方向，只能通过计算得到.短路环流计算方面主要采用的是磁场—电路耦合法[13-14]，在有限元软件中建立变压器磁场模型与外部电路模型.这种方法单次短路工况的求解时间很长，并且由于短路工况的不同，无法一次求解出所有短路工况下的复合短路阻抗，也就无法避免重复计算带来的时间浪费.

针对以上复合短路阻抗与短路环流求解存在的应用范围狭窄与时效性不足等问题，本文提出了一种基于新型磁场—电路耦合理论的求解方法.首先利用ANSOFT磁场仿真软件，一次求解所有绕组的电感矩阵；再于MATLAB软件中，围绕利用ANSOFT软件得到的电感矩阵搭建电路；在忽略励磁电流的情况下，从电路上计算多绕组变压器复合短路阻抗及各种短路工况下各绕组的电流环流.与以往的计算方法相比，这种计算方法既能避免复杂的计算公式带来的错误，又能大幅降低复合短路阻抗及短路环流计算时间，具有简明、高效的特点.

1 新型磁场-电路耦合计算方法

新型磁场-电路耦合理论的基本思路是：1)将电气元件由图纸模型转换为磁场模型；2)通过磁场模型导出该元件的数学模型；3)再利用数学模型与电路耦合，得到电气元件的电路模型.具体到多绕组变压器复合短路阻抗与短路环流计算，按照以下步骤：1)通过变压器磁场仿真计算，得到变压器所有绕组的自感与互感矩阵，将变压器从图形上的磁场结构转换为数学结构；2)将得到的电感矩阵导入到MATLAB环境下的耦合电感元件中，通过在耦合电感元件外围添加电源、导线、电量测量元件等，构成变压器短路电路模型，从而实现将变压器由数学结构转换为电路结构；3)通过电路仿真，得到多绕组变压器复合短路阻抗及短路环流数据；4)该计算方法按照多绕组变压器短路稳态运行的工作情况：①短路情况下的变压器励磁电流很小，可以忽略不计．②变压器绕组的短路阻抗由短路电抗与短路电阻组成，其中短路电阻远小于短路电抗.

1.1 简化变压器磁场模型与电感矩阵

静态磁场中，由麦克斯韦电磁方程得：

(1)

设变压器绕组A与绕组B置于同一铁心上.由电流I施加于绕组A上的自感磁链为ψAA，对绕组B的互感磁链为ψAB，则有：

(2)

利用ANSOFT磁场仿真软件求解变压器及其电磁边界空间内的每个单元由电流I产生的磁感应强度BvA与磁场强度HvA.由式(1)有：

(3)

其中e=1,…,N为多材料的模型.

结合式(2)和(3)可求得变压器绕组A自感LAA.

对于绕组B，则有：

(4)

同理可知电流I在绕组B上的磁链ψAB为：

(5)

由此可求得绕组A与绕组B的互感MAB.

在ANSOFT软件中建立简化多绕组变压器磁场模型，如图1所示，在简化磁场模型中施加电流激励并取得所有绕组的单匝电感矩阵.

图1 多绕组变压器简化磁场模型

设多绕组变压器绕组编号为：1，2，…，n.其中i号绕组匝数为Ni，流过该绕组的电流为Ii.变压器磁场模型简化方式为：将变压器i号绕组的匝数Ni按照单匝绕组建模，即：

Ni=1;i=1,2,…,n

(6)

加载相应绕组电流：i1,i2,…，in，可得简化变压器绕组的电感矩阵[m]：

(7)

式中li为简化变压器模型i号绕组的自感;mij为j号绕组对i号绕组的互感.

当变压器中i，j号绕组单独发生短路，由电感的定义可知：

(8)

式中ψii为单匝绕组i与自身交链的磁链，ψji为单匝绕组j对单匝绕组i的磁链.

在非简化的多匝绕组情况下两两绕组发生交链时：

(9)

其中

联立(7)，(8)与(9)式可得多绕组变压器自感与互感组成的电感矩阵[M]

(10)

其中

由以上推导可知，建立简化有限元磁场模型，在ANSOFT磁场仿真软件中，可以通过设定绕组匝数得到多绕组变压器的所有绕组的电感矩阵[M].

变压器在额定工作状态与短路工作状态下，铁心均工作在其B-H曲线线性区内，铁心相对磁导率保持恒定，励磁电流均可忽略不计，因此认为额定工作状态与短路工况下的绕组电感矩阵是保持不变的.

1.2 基于电感矩阵的复合短路阻抗与短路环流计算

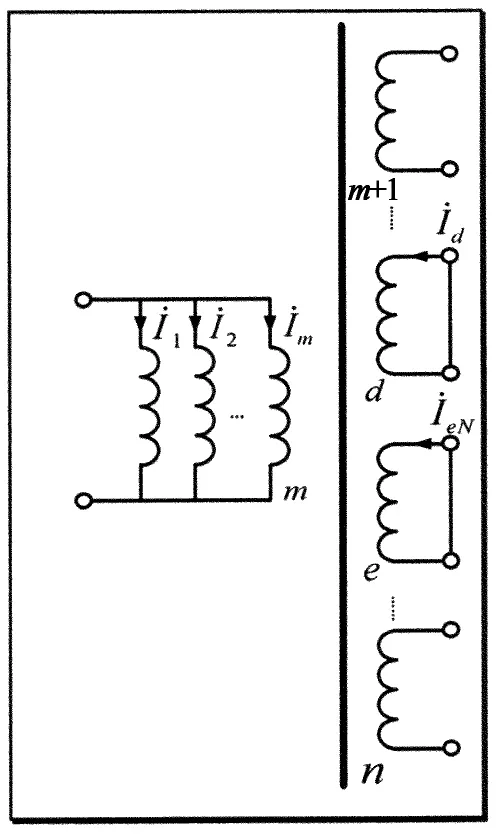
多绕组变压器各绕组电压与电流正方向如图2所示[15-16].其中绕组1到绕组m为高压绕组，绕组m+1至绕组n为低压绕组，各绕组额定电压不同，绕组绕线结构等也不尽相同.

由多绕组变压器电压电流示意图，可对每个绕组列写多绕组变压器电量方程，并成为多绕组变压器电量方程组：

(11)

将式(11)改写为矩阵形式：

(12)

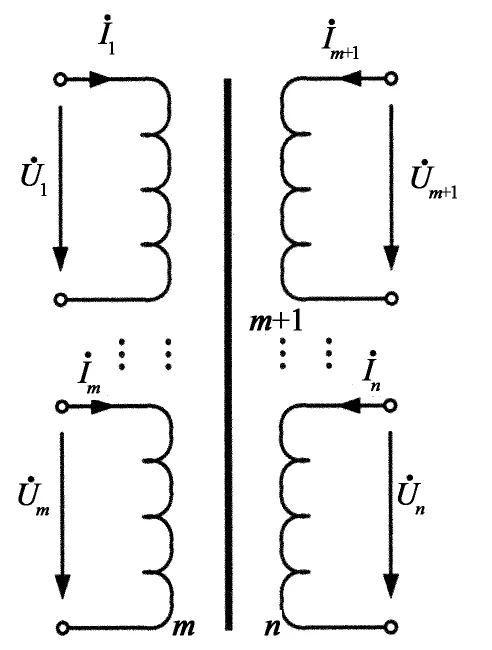
图2 多绕组变压器电压电流示意图

电阻矩阵[R]可由绕组面积、绕组长度、绕组材料等得到.由式(12)可知，多绕组变压器电量方程组中的电感矩阵[M]由上节简化磁场模型换算得到，在求解过程中为已知量，电阻矩阵[R]亦为已知量，各绕组的电压与电流共2n个未知量待求解.通常n个1次方程无法求得2n个未知量，因此通过变压器不同短路工况下的电压电流状态进行分析，对式(12)中的电压与电流向量增加端口条件，即将2n个未知量中的n个或更多个未知量变为已知量，对剩余的n个或更少的未知量进行求解，从而得到电量方程的确定解，即所有绕组的短路电压与短路环流.

多绕组变压器大多采用高压绕组并联供电、低压绕组单独供电的模式，其短路工况大致分为以下3种：1)高压绕组并联供电，某一低压绕组发生短路；2)高压绕组并联供电，多个低压绕组发生短路；3)高压绕组断开，某一低压绕组供电，另一低压绕组短路.

对于短路工况1)，多绕组变压器端口条件为：

(13)

(14)

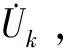
(15)

根据3种不同的短路工况，分别得到不同短路工况下的电路模型，如图3所示.

由式(14)，(15)和(13)可分别计算不同短路工况下所有绕组的电压与电流.复合短路阻抗计算值往往采用短路阻抗百分比来表示，即短路情况下提供电源的绕组两端的电压与这一绕组的额定电压之比，即：

(16)

1.3 短路工况与电路模型搭建

由上节推导可知，只需要确定了多绕组变压器的短路端口条件，就可以列写短路条件下的电量方程，并通过解方程来求解复合短路阻抗与短路环流，这一求解过程将利用矩阵变换、多元方程求解等手算方法，在实际求解过程中需要大量计算时间来完成；如利用计算机编制计算程序完成求解，由于多绕组变压器种类多样，绕组串并联关系多变且复杂，求解复合短路阻抗的短路工况端口条件多，难以设计一个统一的计算软件来实现对所有种类的多绕组变压器多个复合短路阻抗求解，各短路工况下的绕组短路环流亦无法得到.由此出发，提出通过将ANSOFT有限元磁场仿真软件得到的多绕组变压器的电感矩阵[M]导入MATLAB电路仿真软件的耦合电感元件中，通过围绕耦合电感元件结合不同短路工况来搭建外围电路的方式，对变压器实际运行情况进行电路仿真，从而求解多个复合短路阻抗及绕组的短路环流.

通过搭建不同短路工况下的MATLAB电路仿真软件电路模型并进行仿真，可得到不同短路工况下的复合短路阻抗及短路环流.仿真方法为逐次试测不同短路电压情况下的短路绕组电流，直到短路绕组电流值为额定电流为止，记录下这一仿真状态下的电源电压与各绕组的电流值与电流相位.

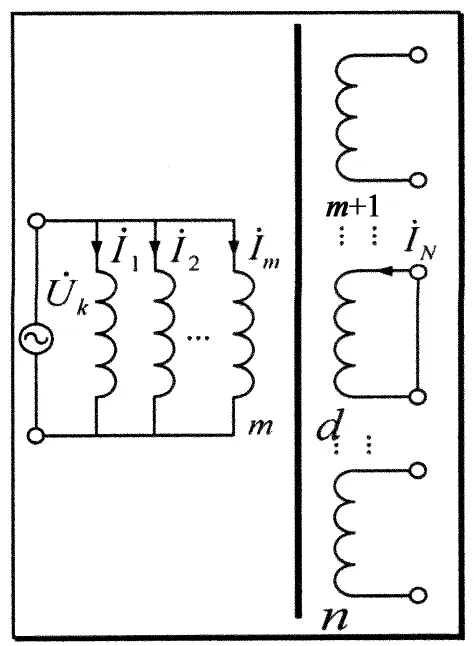
(a) 短路工况1X

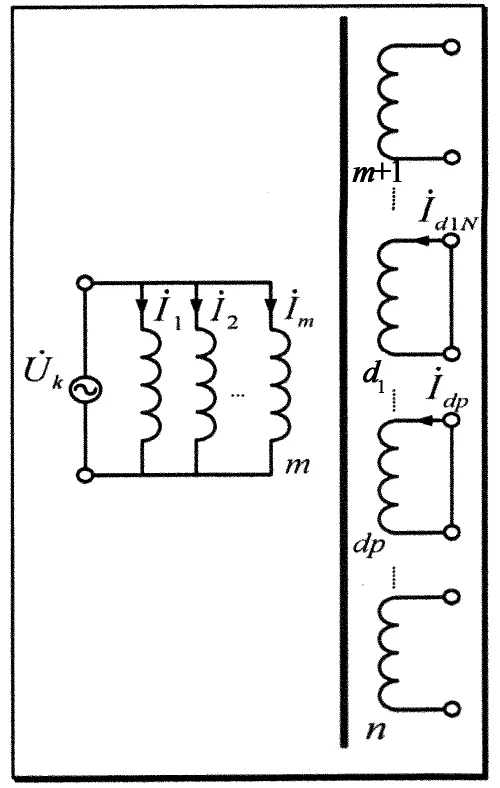
(b) 短路工况2X

(c) 短路工况3X

2 实验验证

实验对象为某电力机车8绕组牵引变压器，H1～H4号绕组为并联的高压绕组，L1～L4号绕组为独立的低压绕组.通过新型磁场—电路耦合计算方法，可先通过建立变压器简化有限元磁场模型，得到所有绕组的电感矩阵，如式(17)所示；再通过电感矩阵与短路电路工况结合，得到变压器所有绕组的复合短路阻抗及短路环流，如表1所示.由表1可知：1)采用基于新型磁场—电路耦合计算方法得到的变压器复合短路阻抗值与实测值最大误差在5%以内，满足工程需求；2)不同的变压器短路工况对应不同的绕组短路电流分布情况；3)变压器高压绕组对某一低压绕组短路时，各高压绕组内的电流是不同的，这主要是由绕组排布不同导致的耦合度不同造成的；4)某一低压绕组供电，另一低压绕组短路的工况下，由于高压绕组并联，不同的高压绕组对低压绕组的互感不同，因此在并联的高压绕组中存在环流，在变压器耦合度平衡设计中应引起注意，并且适当提高高压绕组的绝缘等级，避免绕组过流引起的变压器绕组烧毁.

[M]=

(17)

利用文献[10]中提出的场路耦合计算方法，与利用文献[8]中提出的数学计算方法，得到复合短路阻抗与短路环流计算结果见表2.由表2可知场路耦合计算方法、数学计算方法与本文提出的方法计算结果基本一致，由此可验证本文计算方法的正确性，但文献[10]中场路耦合计算需要结合铁心B-H曲线进行非线性计算，总体计算时间冗长；文献[8]中数学计算方法需要计算两两绕组的短路阻抗，并利用短路阻抗矩阵进行矩阵转换来得到计算结果，计算过程较为复杂，可由矩阵计算软件编制计算程序完成.

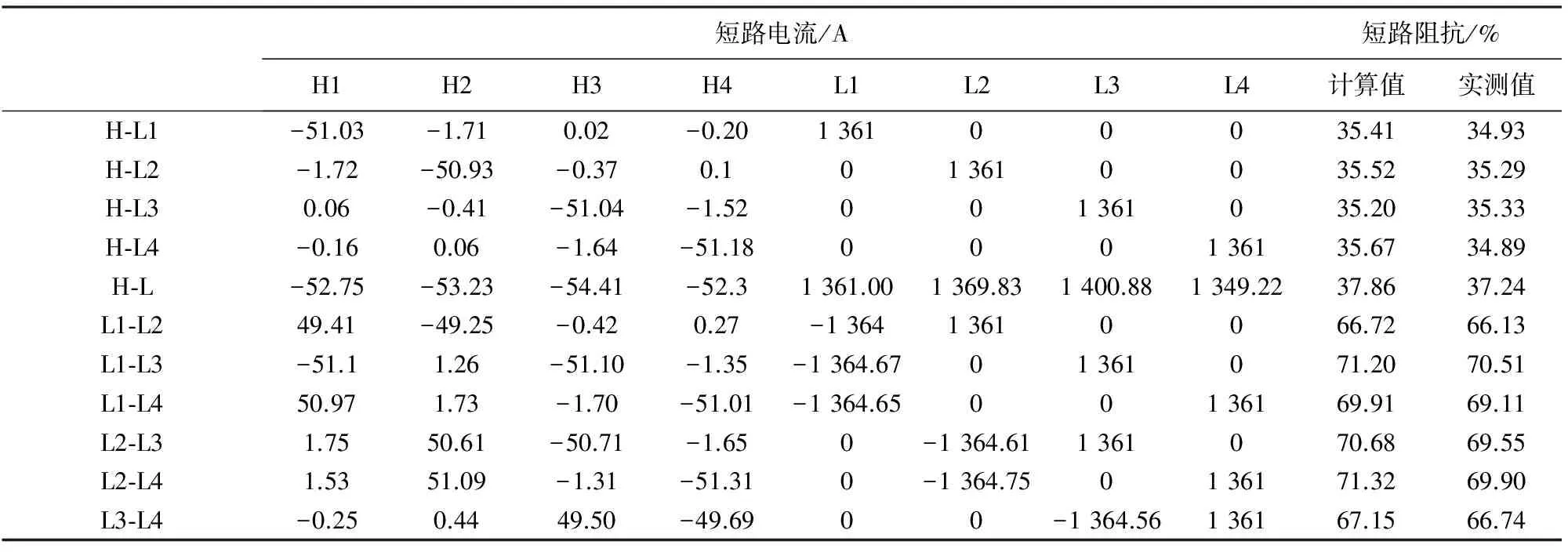
表1 多绕组变压器复合短路阻抗与短路环流计算与实测值

注：表1中H-L1，H-L2，H-L3，H-L4分别表示所有高压绕组对单个供电绕组；H-L表示所有高压绕组对所有供电绕组；L1-L2，L1-L3，L1-L4，L2-L3，L2-L4，L3-L4分别表示单个供电绕组对单个供电绕组.

表2 几种计算方法的短路环流计算值对比

3 结 论

本文提出基于新型磁场—电路耦合方法的多绕组变压器复合短路阻抗计算的新方法.该方法利用ANSOFT磁场仿真软件与MATLAB电路仿真软件结合，通过电感矩阵作为连接磁场与电路连接的桥梁，对传统的场路耦合算法与数学计算方法进行改进，从而得到一种简洁、直观的多绕组变压器复合短路阻抗计算的新方法.利用新方法对电力机车8绕组牵引变压器进行计算.实验与计算结果表明该计算方法具有可用性强，计算精度高的特点，完全可满足工程设计的要求.将新方法与传统场路耦合方法，数学计算方法得到的短路环流进行列表对比，3种计算方法的短路环流计算结果基本一致，从而验证了新方法在计算短路环流方面的正确性.

传统磁场—电路耦合方法建立电气元件磁场模型，将电源等传统的电路元件作为简化磁场元件，一并导入磁场仿真软件模型进行多次计算，每次计算均对时变磁场及元件关于时间点的磁状态进行一次仿真；新型磁场—电路耦合计算方法首先得到描述电气元件磁场特性的数学表达式，再将数学表达式代入电路仿真软件中的电路元件进行多次计算，每次计算均对时变电路及电气元件关于时间点的电状态进行一次仿真；传统磁场—电路耦合仿真方法与新型磁场—电路耦合仿真方法从本质上来说都是将磁场与电路两个物理场进行耦合仿真，其计算方法的差别仅仅体现在对磁场进行简化或对电路进行简化；相对于磁场仿真来说，电路仿真的耗时相对要小得多，因此新型磁场—电路耦合方法具有优越的时效性.

[1] 孙秋霞, 韩强, 王法庆,等.多绕组变压器阻抗的容量加权计算与数值分析 [J].变压器, 2011, 48(1):7-10.

SUN Qiu-xia, HAN Qiang, WANG Fa-qing,etalPower weighted calculation and numerical analysis for impedance of multi winding transformer[J] .Transformer, 2011,48(1):7-10.(In Chinese)

[2] 韩芳旭, 李岩, 孙昕,等.电力变压器漏磁场和短路阻抗计算 [J].变压器, 2010, 47(10):9-12.

HAN Fang-xu, LI Yan,SUN Xin,etalCalculation of leakage magnetic field and short circuit impedance of power transformer [J]. Transformer, 2010, 47(10):9-12. (In Chinese)

[3] 唐起超, 王赞基, 王维俭，等.多绕组电力变压器内部短路稳态分析 (一)建模与仿真[J].电力系统自动化,2006,30(10):44-47,74.

TANG Qi-chao, WANG Zan-ji, WANG Wei-jian,etalSteady-state analysis of internal short circuits of multi-winding power transformer part I modeling and simulations [J]. Automation of Electric Power Systems, 2006, 30(10):44-47,74. (In Chinese)

[4] 田贵书, 刘亚民, 赵忠云. 海洋平台用多绕组树脂浇注干式变压器[J]. 变压器, 1998, 35(9): 34-35.

TIAN Gui-shu, LIU Ya-min, ZHAO Zhong-yun. Multiwinding resin cast dry-type transformer for sea-platform [J]. Transformer, 1998, 35(9): 34-35. (In Chinese)

[5] 田军, 陈乔夫, 张宇. 多绕组变压器负载可控型可调电抗 [J]. 电力自动化设备, 2010, 30(1): 31-35.

TIAN Jun, CHEN Qiao-fu, ZHANG Yu. Adjustable reactor with controllable load of multi-winding transformer [J]. Electric Power Automation Equipment， 2010, 30(1): 31-35．(In Chinese)

[6] 邓海生, 陈东风, 林刚,等. 高-低-高-调排列双绕组有载调压变压器短路阻抗计算方法分析[J].变压器,2010,47(7):1-5,71.

DENG Hai-sheng, CHEN Dong-feng, LIN Gang，etal. Analysis of calculation methods for short circuit impedance of double-winding on-load-tap-changing transformer with arrangement of HV-LV-HV-votage regulation windings[J]. Transformer, 2010, 47(7):1-5,71. (In Chinese)

[7] (苏)瓦休京斯基(С.Б.Васютинский)著. 变压器的理论与计算[M]. 北京：机械工业出版社, 1983.

ВАСЮТИНСКИЙ С Б. Theory and calculation of the transformer[M]. Beijing: China Machine Press,1983.(In Chinese)

[8] 罗隆福，张志文，邓建国，等．多绕组变压器复合短路阻抗的求解方法 [J]. 电工技术学报，2002，17(3)：146-152．

LUO Long-fu, ZHANG Zhi-wen, DENG Jian-guo,etal．The method solving composite short-circuit impedance of multi-winding transformer[J]. Transactions of China Electrotechnical Society, 2002, 17(3): 146-152. (In Chinese)

[9] 王世山, 李彦明, 郭颖娜,等. "磁场-电路"耦合法计算变压器短路阻抗[J]. 高电压技术, 2006, 32(11):11-14.

WANG Shi-shan, LI Yan-ming, GUO Ying-na，etal. Calculation of short-circuit impedance for power transformer with coupling FEM method of magnetic field and circuit[J]. High Voltage Engineering, 2006, 32(11):11-14. (In Chinese)

[10]NOWAK L, KOWALSKI K. The 3D coupled field-circuit simulation of transients in nonlinear systems[J]. Magnetics. IEEE Transactions on, 1996, 32:1078-1081.

[11]KUMBHAR G B, KULKARNI S V. Analysis of short-circuit performance of split-winding transformer using coupled field-circuit approach[J]. Power Delivery, IEEE Transactions on, 2007, 22:936-943.

[12]LUO L, LI H, LI Y,etal. Study on the electromagnetic transient state in the new converter transformer based on coupled field-circuit method[C]//IEEE International Conference on Electrical Machines and Systems. Wuhan, China,2008: 4291-4295.

[13]李晓松, 胡贵, 龙谷宗,等. 基于“场一路”结合分析的高速动车组主变压器稳态特性计算[J]. 长沙理工大学学报:自然科学版, 2011, 8(3): 50-55.

LI Xiao-song, HU Gui, LONG Gu-zong,etal. Calculation of the steady state performances of a transformer equipped in a train set with power car based on combined field-circuit method[J]. Journal of Changsha University of Science and Technology:Natural Science,2011, 8(3): 50-55. (In Chinese)

[14]阎秀恪,李晓玉,谢德馨,等.变压器连续式绕组的环流计算与换位研究[J].变压器,2008,45(5):1-4,21.

YAN Xiu-ke, LI Xiao-yu, XIE De-xin,etalCirculating current calculation and transposition research of continuous winding in transformer[J]. Transformer, 2008,45(5):1-4,21. (In Chinese)

[15]辜承林, 陈乔夫, 熊永前. 电机学[M]. 武汉:华中科技大学出版社, 2005,122-127.

GU Cheng-lin, CHEN Qiao-fu, XIONG Yong-qian. Electric machinery[M]. Wuhan: Huazhong University of Science& Technology Press, 2005: 122-127. (In Chinese)

[16]崔立君. 特种变压器理论与设计[M]. 北京:科学技术文献出版社, 1996:20-21.

CUI Li-jun. Theory and design of special transformer[M]. Beijing: Scientific and Technical Documentation Press, 1996: 20-21. (In Chinese)

Multi-winding Transformer Composite Short-circuit Impedance and Circulating Current Calculation Based on A New Field-circuit Coupling Method

LUO Long-fu，LIAO Wen-di†， XU Jia-zhu， LU Sai

(College of Electrical and Engineering, Hunan Univ, Changsha,Hunan 410082，China)

The short-circuit impedances of multi-winding transformers vary in different short-circuit states, which are called composite short-circuit impedances. With different short-circuit states, the circulating currents of the windings are different. It takes a long time to solve the composite short-circuit impedance and the circulating current, and there are some difficulties in solving the formulas of the transformer. Aiming at the problems above, a new calculation based on a new field-circuit coupling method was provided. By building the simplified magnetic field model, the inductance matrix of all the transformer windings was obtained. The external circuit and the inductance matrix were combined, and the composite short-circuit impedances and the circulating currents of the multi-winding transformer can be obtained quickly. Taking a 8-winding transformer for instance, the measurement results show that this new calculation method is of high accuracy, low consuming time and high engineering value.

new field-circuit coupling calculation method；composite short-circuit impedance； short-circuit circulating current； multi-winding transformer

1674-2974(2015)02-0067-07

2014-05-11

国家自然科学基金资助项目(51077045),National Natural Science Foundation of China(51077045)

罗隆福(1962-)，男，湖南常德人，湖南大学教授，博士生导师†通讯联系人，E-mail:liaowendi@hnu.edu.cn

TM.47

A