3,4-二硝基呋咱基氧化呋咱的结晶热力学

侯　欢，王建龙 ，陈丽珍，兰贯超，李　静，李　满

(中北大学化工与环境学院，山西太原030051)



3,4-二硝基呋咱基氧化呋咱的结晶热力学

侯欢，王建龙 ，陈丽珍，兰贯超，李静，李满

(中北大学化工与环境学院，山西太原030051)

摘要：在大气压力及298.15～338.15K下采用激光动态法测定了3,4-二硝基呋咱基氧化呋咱(DNTF)在不同体积比的乙酸-水混合溶剂中的溶解度，用Apelblat和(CNIBS)/Redlich-Kister经验模型对溶解度数据进行拟合，根据溶解度实验数据估算了DNTF的标准溶解焓、标准溶解熵、标准吉布斯自由能、固-液表面张力以及表面熵因子。通过测定DNTF在乙酸-水混合溶剂中的超溶解度，得到DNTF的冷却结晶介稳区，探讨了溶剂组成和温度对溶解度的影响。结果表明，用Apelblat模型和(CNIBS)/Redlich-Kister模型计算的溶解度值与实验值的平均相对误差分别为1.698%和3.001%；DNTF在乙酸-水溶液中的溶解度随温度的升高和乙酸含量的增加而增大；介稳区宽度随温度的增加而变宽，随乙酸含量的增大而变窄。

关键词：有机化学；3,4-二硝基呋咱基氧化呋咱；DNTF；冷却结晶；热力学；溶解度；介稳区

引言

3,4-二硝基呋咱基氧化呋咱(DNTF)为无色无味的白色晶体，其综合性能优于奥克托今(HMX)，接近六硝基六氮杂异戊兹烷(CL-20)，不仅可作为炸药，同时也可作为推进剂的成分[1-4]，具有广阔的应用前景。含能材料的晶体颗粒品质对其机械强度、感度和输出能量都有影响。结晶过程中，溶剂的选择、结晶温度、过饱和度、搅拌强度等外部因素都会影响晶体的生长，因此需要对含能材料的结晶过程进行研究，研究方法主要有冷却和溶析两种。胡金伟等[5]研究了TNAZ的结晶过程。为了进一步提高DNTF的晶体品质，需要通过重结晶过程控制晶体形貌。

结晶过程的推动力主要来自于结晶多相体系在热力学上的非平衡特性，因此结晶过程的研究通常是从研究其热力学行为开始，溶解度和超溶解度等结晶热力学数据的测定是设计结晶器、确定结晶工艺最佳操作条件的基础。激光动态法用于测定黑索今等炸药的溶解度和超溶解度，确定结晶介稳区。

本研究采用激光动态法测定DNTF在乙酸与水混合物中的溶解度和超溶解度，拟合了溶解度实验数据，讨论了乙酸含量对介稳区宽度的影响，为DNTF的结晶工艺优化及工业放大提供基础数据。

1实验

1.1材料及仪器

DNTF，重结晶后纯度大于99.5%，西安近代化学研究所；乙酸，分析纯，纯度大于99.5%，国药集团化学试剂有限公司；蒸馏水，实验室自制。

电子天平，精度±0.0001g，梅特勒-托利多仪器有限公司；500mL夹套结晶器、移液管，太原迎新街玻璃厂；恒温水浴，精度±0.01℃，巩义市予华仪器有限责任公司；磁力搅拌器，杭州仪表电机有限公司；温度计，北京中西远大科技有限公司；He-Ne激光器，北京大学物理系。

1.2溶解度测定方法

激光动态法[6]测定溶解度的原理是由晶体管激光发射器、光电转换器和光强数码显示仪组成的激光监测系统被用来代替人眼观察固体的溶解状况并判断测定终点的到达，测定过程有较高的准确性，且具有方便、快捷、灵敏等优点，测定装置如图1所示。首先打开激光装置预热30min；准确量取一定量的溶剂和溶质，加入到结晶器中，设置温度及搅拌速率，开启恒温装置和搅拌装置；升温过程中观察精密水银温度计温度和光强示数的变化，当结晶器内达到预置温度并稳定20min后，记录透射光强；用滴管逐次缓慢加入少量溶剂，记录透射光强及加入的溶剂量；当透射光强示数达到最大并且在30min内无明显变化时，认为溶质已经完全溶解，记录的温度即为溶解温度，该温度点下的溶解度，可通过所加入的溶质和溶剂质量计算得到。然后继续加入一定量的溶质，进行下一个温度点的测定。

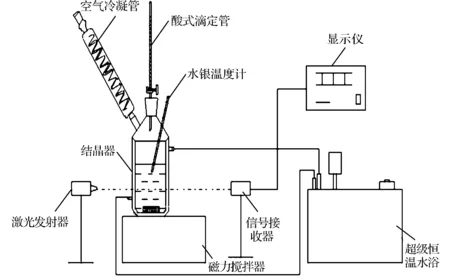
图1　溶解度测定装置示意图Fig.1　Schematic diagram of the measurementsetup of solubility

1.3介稳区测定方法

标志溶液过饱和而欲自发产生晶核的极限浓度曲线称为超溶解度曲线，溶解度平衡曲线与超溶解度曲线之间的区域称为结晶的介稳区[7]。溶液的溶解度曲线与超溶解度曲线不同，对于一个特定的物系，只有一条明确的溶解度平衡曲线，但是超溶解度曲线是一簇曲线。因此，在工业结晶条件下得到的超溶解度曲线和介稳区宽度对结晶工艺设计非常重要。

采用激光动态法测定DNTF在乙酸-水混合溶剂中的超溶解度，其结晶工艺条件为搅拌速率300r/min，降温速率0.1K/min。首先，把精确称量的溶质和溶剂加入结晶器内，开启超级恒温水浴，升温至饱和温度，恒温搅拌30min后，按设定好的测定条件，固定搅拌速率和降温速率，记录开始降温时的温度及时间，当激光信号接收器示数发生突变时，记录此时的溶液温度及时间，即可得到DNTF在该温度下的超溶解度，再结合溶解度曲线即可得到对应的介稳区。

2结果与讨论

2.1溶解度经验模型

Apelblat等[8-9]假定溶液的焓变为温度的线性函数，从Clausius-Klapeyron方程推导出溶解度经验方程

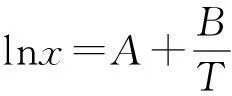
(1)

式中：x为摩尔分数；T为绝对温度，K；A、B、C为模型参数。

针对溶质在混合溶剂体系中的固液平衡问题，Acree等[10-11]提出了(CNIBS)/Redlich-Kister 方程

(2)

式中：x为DNTF在乙酸与水混合溶剂中的溶解度；xi为乙酸的摩尔分数；B0、B1、B2、B3、B4为模型参数。

以上模型均用相对误差RD来检验结果的一致性，即

(3)

式中：xexp为实验值；xcal为计算值。

用平均相对误差∑(RD)来判断用模型拟合得到的实验数据，即

(4)

式中：xexp为实验值；xcal为计算值；n为每个溶剂组成中实验数据的个数。

2.2溶解度实验值与计算值的拟合

乙酸-水混合溶剂中乙酸的含量和DNTF的溶解度均用摩尔分数表示，如式(5)和式(6)：

(5)

(6)

式中：m1、m2、m3分别为DNTF、乙酸和水的质量；M1、M2、M3分别为DNTF、乙酸和水的分子质量；xi和x分别为乙酸和DNTF的摩尔分数。

DNTF在乙酸-水混合溶剂中的溶解度实验值和计算值(以摩尔分数表示)及二者的平均相对误差见表1。

表1　DNTF在乙酸-水混合溶剂中溶解度的实验值和计算值

由表1可以看出，DNTF的溶解度随温度的升高而增大，随乙酸含量的增加而增大。采用Apelblat和(CNIBS)/Redlich-Kister 经验模型对溶解度进行拟合，得到溶解度计算值和实验值的平均相对误差分别为1.698%和3.001%，拟合效果比较好。

2.3不同模型的拟合参数

采用Apelblat和(CNIBS)/Redlich-Kister经验模型对DNTF在乙酸-水混合溶剂中的溶解度数据进行关联，模型参数列于表2和表3中。

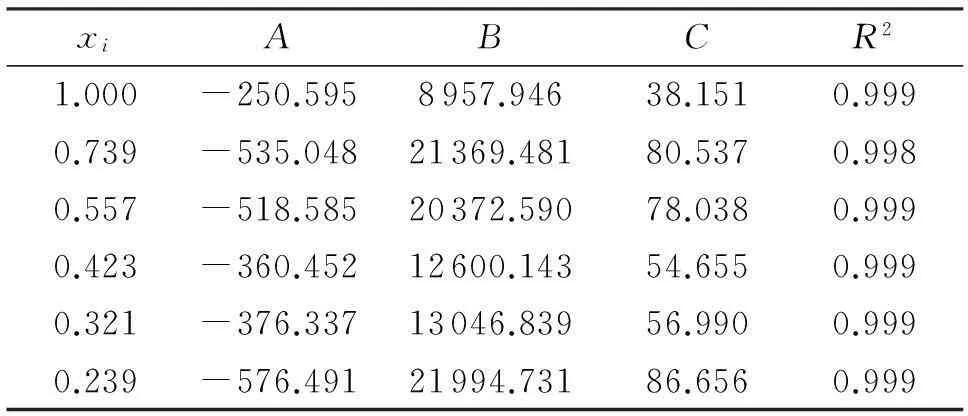
表2　用Apelblat模型所得的DNTF在乙酸-水混合

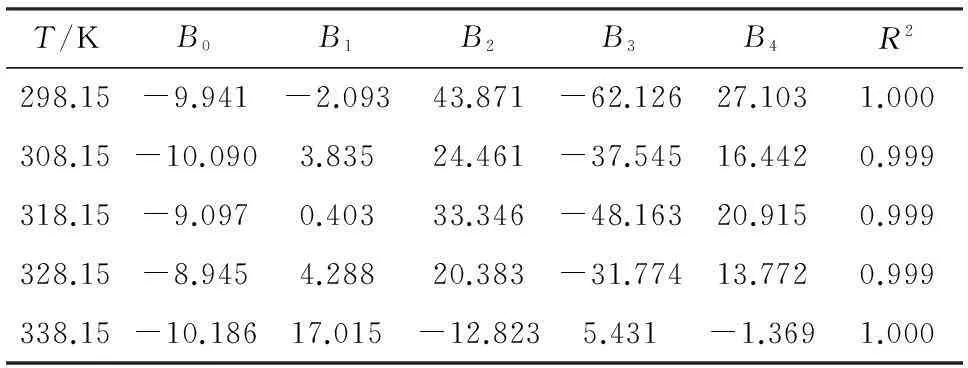
表3　用(CNIBS)/Redlich-Kister模型所得不同温度下

由表2和表3可知，R2值接近于1，说明DNTF溶解度经验模型拟合效果好。因此，根据模型参数可建立DNTF在不同温度和不同乙酸含量中的溶

解度方程。

2.4热力学函数

根据DNTF在不同体积比的乙酸-水混合溶剂中的溶解度，可计算其标准溶解焓、标准溶解熵和标准吉布斯自由能。DNTF的溶解度和绝对温度之间的函数关系可以表示为[12-13]

(7)

式中：R为气体常数，8.3145J/(K·mol)；ΔdisHo和ΔdisSo分别为DNTF的标准溶解焓和标准溶解熵，可以分别从溶解度拟合方程对应线的斜率和截距来计算。DNTF的标准吉布斯自由能可以用式(8)计算，取平均温度T为318.15K。

ΔdisGo=ΔdisHo-TΔdisSo

(8)

溶解过程中焓变和熵变对标准吉布斯自由能的相对贡献值[14-15]ξH和ξS由式(9)和式(10)计算:

(9)

(10)

根据DNTF在不同体积比的乙酸-水混合溶剂中的溶解度以及公式，计算出标准溶解焓、标准溶解熵和标准吉布斯自由能以及在平均温度下计算的ξH、ξS，计算结果列于表4。

表4　DNTF在乙酸-水混合溶剂中的热力学函数值

注：R2为相关系数从表4可以看出，ΔdisHo在所有的混合溶剂中均为正值，表明DNTF的溶解是一个吸热过程。同时，在所有的混合溶剂中ξH大于ξS，说明对标准摩尔吉布斯自由能的主要贡献是焓变，而不是熵变。

2.5固液表面张力及表面熵因子

固液表面张力是代表晶体物理性质的主要物理量，很大程度上决定着晶体的生长机理。Mersmann[16]推导出一个较为简单的表面张力理论计算式

(11)

式中：NA为Avogadro常数(6.02×1023mol-1)；k为玻尔兹曼常数(1.3806×10-23J/K)；ρc为晶体密度，kg/m3；Ceq为晶体溶解度，kg/m3。

表面熵因子(f)是用于表征晶体表面在原子水平上光滑程度的参数。f越大，晶体表面越光滑，生长也越困难。Barata等[17]利用晶体的固液表面张力(γ)，分子体积(V)和温度来近似估算表面熵因子(f)

(12)

式中：V为分子体积，m3/个。

(13)

式中：M为物质的摩尔质量；ρ为密度，g/cm3；NA为Avogadro常数。

根据实验测定的溶解度，计算得到DNTF在乙酸-水混合溶剂中不同温度下的晶体表面张力(γ)，根据表面张力数据求得表面熵因子(f)，见图2。

图2　DNTF在乙酸-水混合溶剂中不同温度下的晶体表面张力和晶体表面熵因子Fig.2　Surface tension and surface entropy factor of thecrystal for DNTF at diffcrent temperatures in aceticacid-water mixed solvent

从图2可以看出，不同乙酸含量的乙酸-水混合溶剂中晶体表面张力和表面熵因子是相同的，混合溶剂中水含量增加，表面张力以及表面熵因子增大。表面张力越大，即表面能越高，表面熵因子越大，即生长能垒越高，晶体生长就越慢。

2.6介稳区宽度

在搅拌速率为300r/min、降温速率为0.1K/min条件下，测定DNTF在不同体积比的乙酸-水混合溶剂中的超溶解度，根据超溶解度数据得到相应的介稳区，见图3。

由图3可以看出，超溶解度曲线与溶解度曲线大致平行，测定的介稳区宽度约为4.65～22.73K，温度升高时介稳区宽度变窄。总体上看，随着混合溶剂中乙酸与水体积比的减小，介稳区宽度增宽。从提高一次结晶收率的角度，应该选择温度对溶解度影响大的条件下操作。但是，结晶工艺应该在介稳区中进行，此时的介稳区太窄，不利于控制。因此选择工艺条件应该综合考虑各方面的因素。

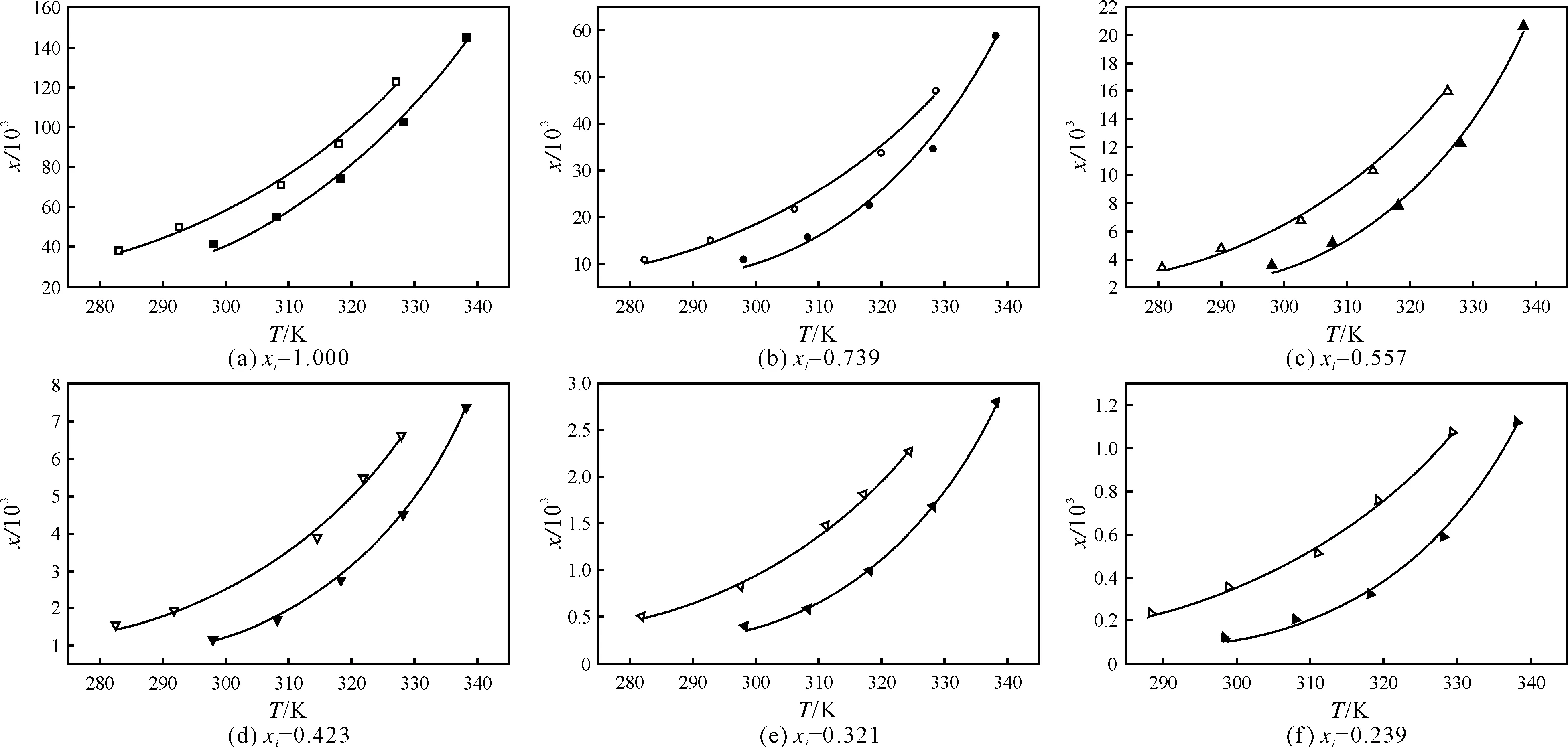
图3　DNTF在不同体积比的乙酸-水混合溶剂中的介稳区Fig.3　Metastable zone of DNTF in acetic acid-water mixed solvent in different volume ratio

3结论

(1)采用激光动态法测定了298.15～338.15K下DNTF在乙酸-水混合溶剂中的溶解度，DNTF的溶解度随温度的升高而增大，随乙酸含量的增加而增大。

(2)用Apelblat和(CNIBS)/Redlich- Kister经验模型拟合了溶解度数据，建立了溶解度方程。

(3)根据溶解度数据估算了DNTF在乙酸-水混合溶剂中不同温度下的热力学函数值。结果表明DNTF的溶解是一个吸热过程。同时，对标准摩尔吉布斯自由能的主要贡献者是焓变，而不是熵变。

(4)测定DNTF在乙酸-水混合溶剂中的冷却结晶介稳区，介稳区宽度随温度的升高而变窄，随乙酸含量的减小而增宽，为DNTF的工业结晶工艺提供了参考。

参考文献：

[1]胡焕性, 张志忠, 赵凤起, 等. 高能量密度材料3,4-二硝基呋咱基氧化呋咱性能及应用研究[J]. 兵工学报, 2004, 25(2):155-158.

HU Huan-xing, ZHANG Zhi-zhong, ZHAO Feng-qi, et al. A study on the properties and application of high energy density material DNTF[J]. Journal of Acta Armamentarii, 2004, 25(2):155-158.

[2]周彦水, 李建康, 黄新萍, 等. 3,4-双(4′-氨基呋咱基-3′)氧化呋咱的合成及性能[J]. 火炸药学报，2007, 30(1): 54-56.

ZHOU Yan-shui, LI Jian-kang, HUANG Xin-ping, et al. Synthesis, and properties of 3,4-bis (4′-furazanyl 3′) furoxan[J]. Chinese Journal of Explosives and Propellants, 2007, 30(1): 54-56.

[3]Sinditskii V P, Burzhava A V, Sheremetev A B, et al. Thermal and combustion properties of 3,4-bis(3-nitrofurazan-4-yl) furoxan (DNTF)[J]. Propellants, Explosives, Pyrotechs, 2012, 37:575-580.

[4]郑伟，王江宁，韩芳，等. DNTF-CMDB推进剂的化学安定性[J]. 火炸药学报, 2010,33(4): 10-13.

ZHENG Wei, WANG Jiang-ning, HAN Fang, et al. Chemical stability of CMDB propellants containing DNTF[J]. Chinese Journal of Explosives and Propellants, 2010, 33(4): 10-13.

[5]胡金伟. TNAZ结晶过程模拟[D]. 太原: 中北大学, 2011.

[6]王莹, 雒廷亮, 李延勋, 等. 己二胺溶解度的测定及关联[J]. 化工中间体, 2008(12): 54-56.

WANG Ying, LUO Ting-liang, LI Yan-yun, et al. Measurement and correlation of solubilities of 1,6-hexane diamine[J]. Journal of Chemical Intermediate, 2008(12): 54-56.

[7]陆杰, 王静康. 普鲁卡因青霉素的结晶热力学[J]. 高校化学工程学报, 1999, 13(3):189-193.

LU Jie, WANG Jing-kang. Crystallization thermodynamics of procaine penicillin[J]. Chinese Journal of Chemical Engineering, 1999, 13(3):189-193.

[8]Apelblat A, Manzurola E. Solubilities of L-aspartic, DL-aspartic, DL-glutamic, p-hydroxybenzoic, o-anisic, p-anisic, and itaconic acids in water formT=278K toT=345K[J]. Journal of Chemical Thermodynamics, 1997, 29:1527-1533.

[9]Apelblat A, Manzurola E. Solubilities of o-acetylsalicylic, 4-aminosalicylic, 3,5-dinitrosalicylic, and p-toluic acid, and magnesium-aspartate in water fromT=(278 to 348) K[J]. Journal of Chemical Thermodynamics, 1999, 31:85-91.

[10]Acree W E. Comments concerning ‘model for solubility estimation in mixed solvent systems’[J]. International Journal of Pharmaceutics, 1996, 127:27-30.

[11]Jouyban-Gharamaleki A, Hanaee J. A novel method for improvement of predictability of the CNIBS/R-K equation[J]. International Journal of Pharmaceutics, 1997, 154:247-254.

[12]ZHOU Li, ZHANG Pei-pei, YANG Guang-de, et al. Solubility of chrysin in ethanol and water mixtures[J]. Journal of Chemical and Engineering Data, 2014, 59:2215-2220.

[13]ZHAO Yan, WANG Yong-li. Determination of the solubility, dissolution enthalpy and entropy of icariin in water, ethanol, and methanol[J]. Journal of Chemical Thermodynamics, 2013, 57: 9-13.

[14]WANG Na, FU Qiang, YANG Guang-de. Determination of the solubility, dissolution enthalpy and entropy of icariin in water, ethanol, and methanol[J]. Journal of Fluid Phase Equilibria, 2012, 324:41-43.

[15]HU Yong-hu, LIU Xiang, YANG Wen-ge, et al. Measurement and correlation of the solubility of 4-methylbenzoic acid in (methanol +acetic acid) binary solvent mixtures[J]. Journal of Molecular Liquids, 2014, 193:213-219.

[16]Mersmann A. Calculation of interfacial tensions[J]. Journal of Crystal Growth, 1990, 102:841-847.

HU Xiao-ling, WU Qiu-jie, QIAN Hua. Synthesis of CL-20 by nitrolysis of TAIW with N2O5/HNO3[J]. Chinese Journal of Explosives and Propellants, 2015, 38(2): 35-38.

Study on Crystallization Thermodynamics of 3,4-Bis (3-nitrofurazan-4-yl)furoxan

HOU Huan, WANG Jian-long, CHEN Li-zhen, LAN Guan-chao, LI Jing, LI Man

(Institute of Chemical Industry and Environment, North University of China, Taiyuan 030051, China)

Abstract:The solubility of 3, 4-bis(3-nitrofurazan-4-yl) furoxan (DNTF) in acetic acid-water mixed solvent in different volume radio was determined in the temperature ranging from 298.15 to 338.15K by the dynamic laser monitoring method under atmospheric pressure. The solubility data were fitted by Apelblat and (CNIBS)/Redlich-Kister experience models. The standard enthalpy of dissolution, standard entropy of dissolution, standard Gibbs free energy, solid-liquid surface tension and surface entropy factor of DNTF were estimated by using the experimental solubility data. The super solubility of DNTF in acetic acid aqueous solution was determined and the metastable zone of cooling crystallization was obtained. The effect of solvent composition and temperature on the solubility was discussed. The results show that the average relative errors of the calculated value and experimental one for solubility data are 1.698% for Apelblat model and 3.001% for (CNIBS)/Redlich-Kister model. The solubility of DNTF in acetic acid-water mixed solvent increases with increasing the temperature and acetic acid content. The width of metastable zone widens with increasing the temperature, and narrows with increasing the acetic acid content.

Keywords:organic chemistry; 3, 4-bis(3-nitrofurazan-4-yl)furoxan; DNTF; cooling crystallization; thermodynamics; solubility; metastable zone

通讯作者:王建龙(1969-)，男，教授，从事含能材料合成研究。

作者简介:侯欢(1990-)，女，硕士研究生，从事含能材料结晶研究。

基金项目:国家自然科学基金(11447219)

收稿日期:2015-06-27；修回日期:2015-09-24

中图分类号：TJ55; O62

文献标志码：A

文章编号：1007-7812(2015)06-0026-06

DOI：10.14077/j.issn.1007-7812.2015.06.006