基于压缩感知的核磁共振成像重构算法
袁 静
(1.宿迁学院计算机科学系,江苏 宿迁223800;2.南京邮电大学信号处理与传输研究院,南京210003)
基于压缩感知的核磁共振成像重构算法
袁 静1,2
(1.宿迁学院计算机科学系,江苏 宿迁223800;2.南京邮电大学信号处理与传输研究院,南京210003)
在核磁共振成像的应用中,一般采用联合方式求解L1范数算子和全变差分算子,而联合正则算子的求解模型比较复杂,为此,利用算子分裂技术求解联合正则算子,以降低求解模型的复杂度。在此基础上,提出一种迭代加权的压缩感知核磁共振重构算法,根据图像在离散傅里叶变换下系数的先验统计特性优化观测矩阵。仿真结果表明,该重构算法不仅提高了算法的重构精度而且减少了重构时间。
压缩感知;迭代加权;核磁共振成像;全变差分L1压缩;算子分裂
DO I:10.3969/j.issn.1000-3428.2015.10.051
1 概述
近年来,Donoho[1]和Candes[2]共同提出了一种新的信号获取理论——压缩感知(Com pressed Sensing,CS)。压缩感知理论的创新之处在于对信号进行采样的同时对数据进行压缩,其采样速率远低于奈奎斯特频率,使得对于海量数据的信号采集变为可能[3-4]。因此,国内外学者从各个方面对这一理论提出了改进和应用[5-7]。
随着人类医疗水平的不断提高,核磁共振成像(Magnetic Resonance Imaging,MRI)已经逐渐成为一种非常重要的医疗辅助技术,而如何加快核磁共振的成像速度一直是该方向的研究热点问题。MRI自身含有压缩感知理论成功应用的2个最为关键的要求[8]:(1)医学图像在某个适当的变换域(比如小波变换等)上是可压缩的;(2)MRI的数据直接在傅里叶域上采样,而不是直接在像素域上[8]。将压缩传感理论应用到核磁共振成像中,可以极大地减少MRI成像所需要的采样数目,从而缩短扫描时间,提高成像效率。文献[9]提出了迭代加权L1范数法。该算法用一个加权的L1范数取代了原来的L1范数问题。由于加权系数的缘故,幅值很小的系数在迭代中会更加趋近于0,这样迭代加权L1
范数法可以获得比L1范数法更加稀疏的解,求解结果更加精确。文献[9]中同时提出了迭代加权TV模型,基本思想和迭代加权L1范数法基本一致。文中的结果表明:迭代加权TV模型的重构效果明显优于一般的TV模型。文献[10]提出了将全变差分正则算子加入到压缩感知重构核磁共振图像的求解模型中,取得了更好的重构效果。文献[11]利用算子分裂思想[12]求解联合正则算子的问题,提出了一种全变差分L1压缩核磁共振(Total Variation L1 Compressed MR Imaging,TVCMRI)算法。
本文引入迭代加权思想对TVCMRI思想进行改进,提出一种重构效果更佳的算法。
2 基于迭代加权的改进求解模型
2.1 求解模型
对于一幅大小为n维的核磁共振图像u,可以通过小波变换Φ获得它的一个稀疏表示:

根据压缩感知的理论,首先通过一个 m×n(m<n)维的观测矩阵R对其进行观测可得:

再考虑式(1)的关系,可以得到:

其中,A=RΦ-1。
已知信号的观测值 b以及观测矩阵 R,就可以利用压缩感知的重构算法求解式(4)的方程来获得图像在小波变换下的稀疏表示χ:

然后,通过对 χ进行小波逆变换就可以重构出原图像,然而在实际应用中,观测值b中总是会含有观测噪声,所以,要对式(4)进行微小的改动,转为求解:

或者式(5)的拉格朗日形式:

其中,σ和μ为参数。
由于核磁共振图像具有分段平滑的性质,也就是说不同的器官其本身应该有一致的结构,因此核磁共振图像应该有很小的全变差分常数。图像的全变差分定义的离散化形式为:
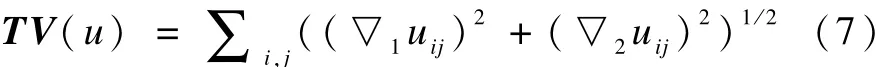
其中,▽1和▽2分别为第一维和第二维上的前向差分算子。
文献[8]提出了将全变差分正则算子加入到压缩感知重构核磁共振图像的求解模型中,取得了更好的重构效果。联合 L1范数和全变差分正则算子的求解模型为:

其中,α和β为2个正的参数。
考虑到基于迭代加权思想的改进 L1范数法和TV模型法相比原方法都有很大的提高,本文考虑利用迭代加权思想对式(8)的求解模型进行改进:其中,W2为一个对角矩阵,其对角线元素2n为加权系数。
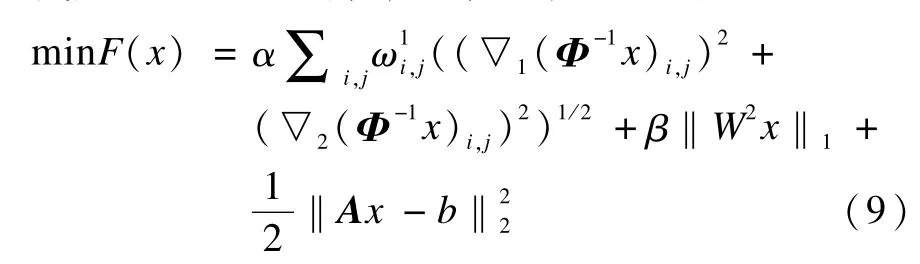
由于全变差分正则算子和 L1范数正则算子对于χ都是非平滑的,因此式(9)所示的求解模型比单独含有L1范数正则算子或者单独含有全变差分正则算子的求解模型要复杂得多。考虑利用算子分裂技术来求解联合正则算子的问题。
2.2 算法推导
在算法推导之前,首先集中介绍推导中用到的几个重要变量,其他变量将在推导中第一次出现时给予解释。变量u∈Rn1×n2表示一幅二维的像素大小为n1×n2的核磁共振图像。算子 L=(▽1,▽2):Rn1×n2→Rn1×n2×Rn1×n2表示沿着第一维坐标和第二维坐标的有限差分算子,它的子算子并且令Ψ=Φ-1,对于任意的正交变换Φ,Ψ=Φ*为Φ的伴随算子。其中,A=
RΨ。根据以上定义的符号,式(9)可以写为:

另外,在推导中还要反复用到泛函的一个性质,对于一个凸函数f(χ)存在以下性质:

下面给出利用算子分裂理论求解式(10)的详细推导过程:
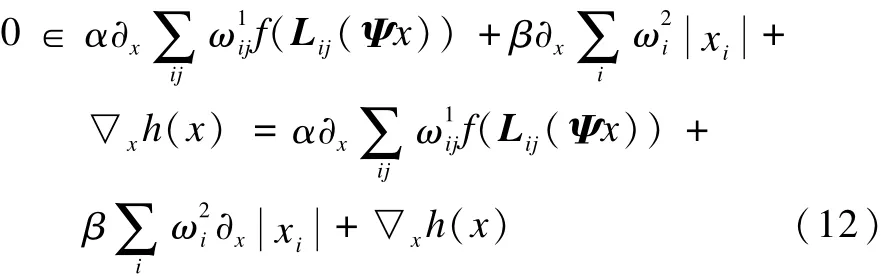
如果算法存在最优解χ,那么必然满足:
其中,∂χ表示对元素χ求导,▽χh(χ)=A*(Aχ-b)= ΦR*(RΨχ-b)。
令Lij(Ψχ)=z,则式(12)变为:

由式(13)可以得出下面2个关系:

根据式(11)的关系,式(15)可以化为:
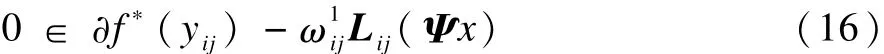
利用算子分裂理论,可以分别对式(14)和式(16)进行处理:
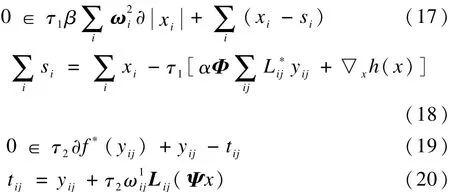
其中,τ1和τ2为2个大于0的参数。
这样,由式(17)~式(20)已经可以比较清楚地看出算法的基本结构了。给定χi和yij,可以分别根据式(18)和式(20)求出si和tij;相反,若已知si和同样可以分别根据式(17)和式(19)算出 χi和 yij。下面推导式(17)和式(19)显示的表达式。
由式(17),有:
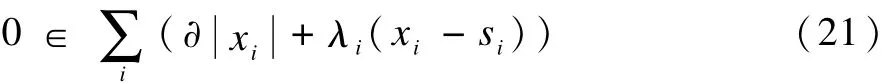
对于绝对值的求导,令:

对于式(19),有:

根据式(11)的关系,有:

移项后,有:
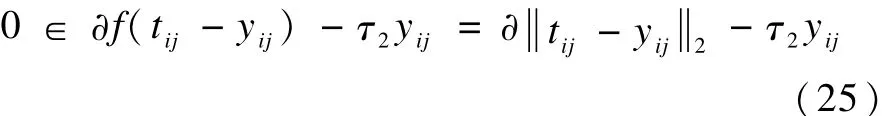
对于2-范数的求导,令:
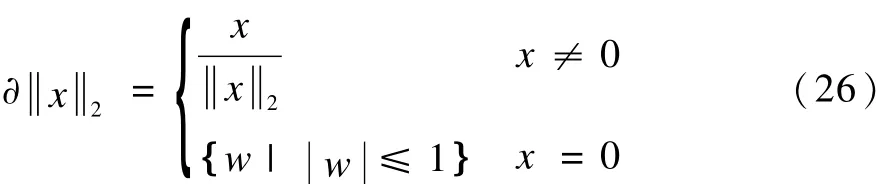
对式(25)进行推导可得:

本文所提出的算法详细步骤为:
输入 核磁共振成像的部分采样值b,算子L和它的伴随算子 L*,部分傅里叶观测矩阵 R,正交小波变换算子Ψ及其逆变换Φ,参数α和 β的衰减速率ηα和 ηβ,以及它们的终值α-和β-,最大迭代次数Maχ,算法终止标准ftol,加权系数中的调整参数ε1和 ε2,步长 τ1和 τ2
输出 重构图像u=Ψχ
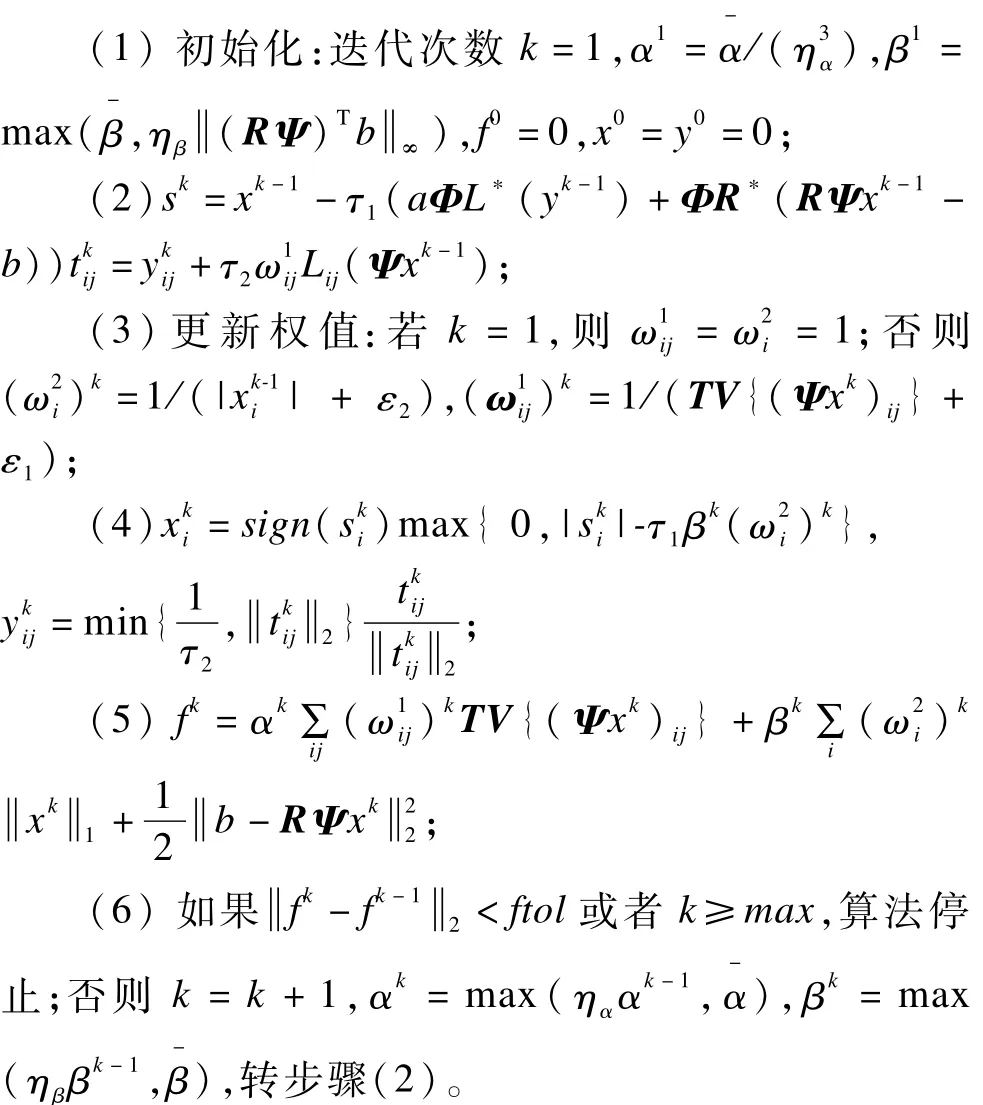
2.3 观测矩阵的优化
在基于压缩感知的核磁共振成像中,观测矩阵R为部分离散傅里叶变换矩阵,可以通过随机选择n×n的离散傅里叶变换矩阵的 m(m<n)行作为观测矩阵R。文献[10]指出,由于核磁共振成像的傅里叶变换的低频能量较高而高频能量较低,因此在
低频选择较多的采样点显得更为有效,并且在文中提出了变密度的采样矩阵。文献[11]中由于离散傅里叶变换的对称性提出了将变换矩阵的上半部分全部(除第一行右半部分)不采样,在下半部分采用变密度采样:越靠近右下和左下的部分采样越多,越靠近中心的部分采样越少。经过比较,发现文献[11]提出的这种观测矩阵的效果要优于文献[10]提出的观测矩阵。
文献[13]提出基于图像在不同变换下的变换系数能量的统计特征的先验知识来优化观测矩阵,取得了更好的重构效果。本文受文献[13]的启发,结合文献[11]中的采样矩阵的结构,提出一种改进的观测矩阵。
对于一幅大小为M×N的图像,首先根据图像在离散傅里叶变换下系数能量的统计特征的先验知识,确定图像中每个点被采样的概率:


图1 采样率为30%时的观测矩阵
本文所提出的观测矩阵确定后,可以保存连续使用。由于利用了图片在离散傅里叶变换下系数的先验统计特性,因此更能够采样到对重构贡献大的系数,获得较好的重构效果。
3 实验结果与分析
本节通过仿真实验证明算法的有效性,所有的程序均在M atlab环境下运行。实验中,设置程序中参数α和β的终值为α-=1×10-3,β-=3.5×10-2,它们的衰减速度分别为ηα=0.25和ηβ=0.25。程序最大的迭代次数Maχ=20,程序终止条件ftol=1× 10-3,程序步长τ1=τ2=0.8,加权系数中的调整系数分别为ε1=0.2,ε2=20。观测中混入的高斯白噪声方差为σ2=1×10-4。
利用仿真程序测试了4种不同人体器官的核磁共振图像:210×210的脑部图像,220×220的胸部图像,220×220的肾脏图像以及208×924的人体全身图像。
图2显示采样率为 20%时胸部的重构图像,图2(a)为原始图像,图2(b)为TVCMRI算法的重构图像,图2(c)为利用本文提出的改进观测矩阵TVCMRI算法的重构图像,图2(d)为本文提出算法的重构图像。可以看出,TVCMRI算法作为一种求解联合L1范数和TV模型的有效算法,在采样率为20%的情况下可以很好地对原图像进行重构。利用本文提出的优化的观测矩阵,TVCMRI算法(在后面的图中用TCM 1表示该算法)的重构图像更加明亮,表明优化的观测矩阵的采样能量更为丰富。而本文算法的重构效果显然更好,人体器官的一些复杂的细节也得到了较好的重构。
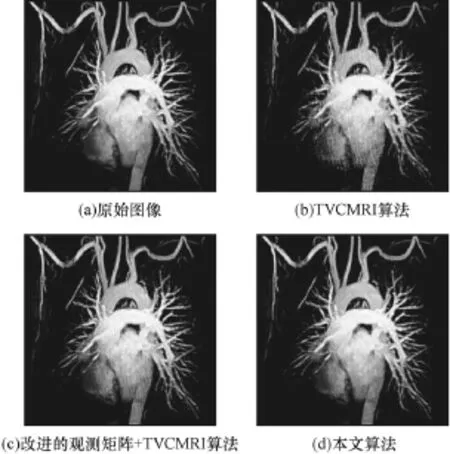
图2 采样率为20%时的重构图像
表1记录了仿真实验中3种算法在不同采样率下不同部位图像重构的峰值性噪比和重构时间。图3显示了不同采样率下3种算法重构图像的峰值信噪比的平均值。从图中可以看出,利用本文提出的优化的采样矩阵,TVCMRI重构图像的峰值信噪比可以获得2 dB左右的提高。由于引入了迭代加权思想,本文提出的改进算法较之原来的TVCMRI算法在采样率相同并且都使用优化的观测矩阵的情况下,峰值信噪比可以获得3 dB~5 dB的提高。从图中可以发现,利用本文提出的改进算法和优化的
观测矩阵,相比于原来的TVCMRI算法和观测矩阵,在相同的重构效果要求下可以节省10%的观测数据量。
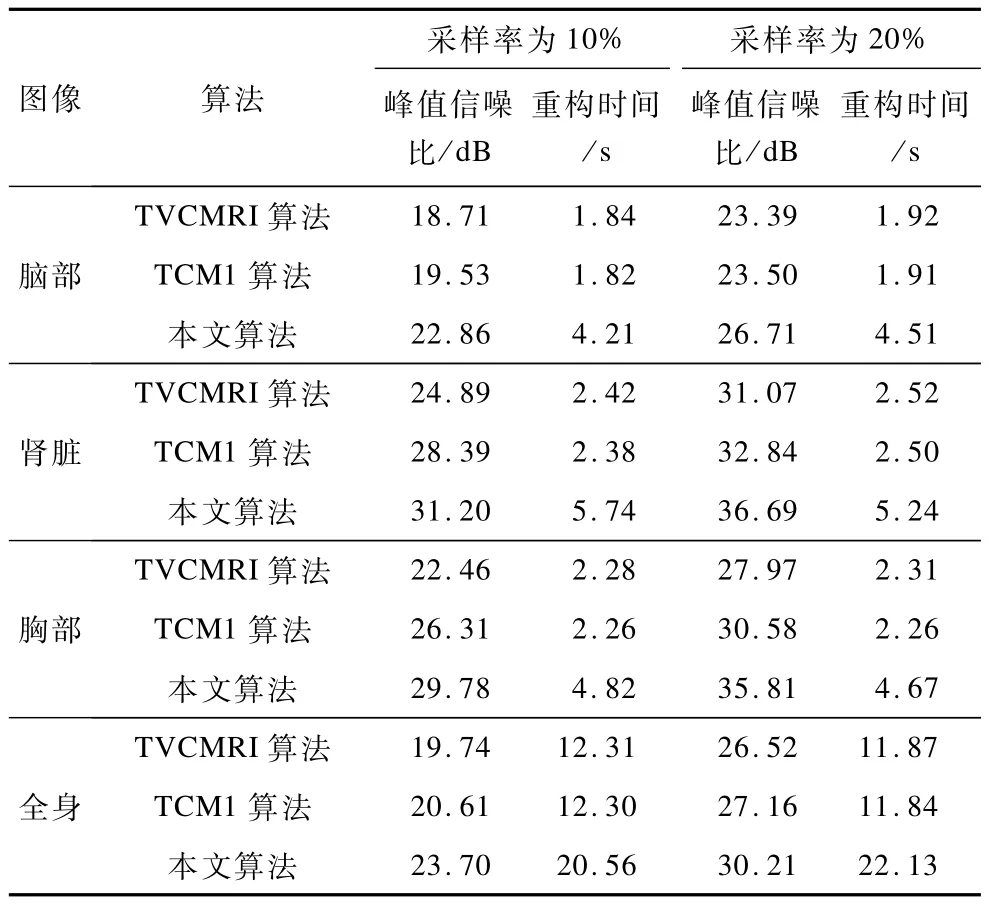
表1 图像的峰值信噪比和重构时间比较

图3 不同采样率下算法重构图像的峰值信噪比
从表1中也可以看到,本文所提出的改进算法的计算时间大概为原TVCMRI算法的2倍。但是由于该算法在相同的重构要求下可以节省10%的采样数据,也就是可以大幅减少患者的核磁共振扫描时间,相比后端重构所多出的这点时间可以忽略不计。
4 结束语
压缩感知技术在核磁共振成像中有着广阔的应用前景。本文利用算子分裂技术和迭代加权思想改进了求解模型,提出了迭代加权的联合L1和全差变分正则算子模型,并且推导出了基于算子分裂技术的重构算法,同时优化了观测矩阵。仿真实验证明了改进算法的有效性,但从仿真实验中也可以看出改进算法的计算时间有所延长,今后将进一步利用平滑技术对重构算法进行优化,以降低算法重构的运行时间。
[1] Donoho D L.Compressed Sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[2] Candes E.Compressive Sampling[C]//Proceedings of International Congress of Mathematicians,Madrid,Spain:[s.n.],2006:1433-1452.
[3] 李少东,杨 军,马晓岩.基于压缩感知的ISAR高分辨成像算法[J].通信学报,2013,34(9):150-157.
[4] 宁方立,何碧静,韦 娟.基于lp范数的压缩感知图像重建算法研究[J].物理学报,2013,62(17):174-212.
[5] 冯 振,郭 禾,王宇新,等.CS-MRI中稀疏信号支撑集混合检测方法[J].计算机工程,2014,40(5):164-167.
[6] 史久根,吴文婷,刘 胜.基于压缩感知的图像重构算法[J].计算机工程,2014,40(2):229-232.
[7] 闫 鹏,王阿川.基于压缩感知的CoSaMP算法自适应性改进[J].计算机工程,2013,39(6):28-33.
[8] Lustig M,Donoho D L,Santos J M,et al.Com pressed Sensing MRI[J].IEEE Signal Processing Magazine,2008,25(3):72-82.
[9] Candes E J,Wakin M B,Body S P.Enhancing Sparsity by Reweighted L1 Minimization[J].Journal of Fourier Analysis and Applications,2008,14(5):877-905.
[10] Lustig M,Donoho D L,Pauly J M.Sparse MRI:The Application of Com pressed Sensing for Rapid MR Imaging[J].Magnetic Resonance Medicine,2007,58(6):1182-1195.
[11] Ma Shiqian,Yin Wotao,Zhang Yin,et al.An Efficient Algorithm for Com pressed MR Imaging Using Tatal Variation and Wavelets[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Washington D.C.,USA:IEEE Press,2008:1-8.
[12] Lions P.L,Mercier B.Splitting Algorithms for the Sun of Two Nonlinear Operators[J].SIAM Journal on Numerical Analysis,1979,16(3):964-979.
[13] Wang Zhongmin,Arce G R.Variable Density Compressed Sampling[J].IEEE Transactions on Image Processing,2010,19(1):264-270.
编辑 顾逸斐
Magnetic Resonance Imaging Reconstruction Algorithm Based on Compressed Sensing
YUAN Jing1,2
(1.Department of Computer Science,Suqian College,Suqian 223800,China;2.Institute of Signal Processing and Transmission,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
In the application of Magnetic Resonance Imaging(MRI),it is common to solve the problem by combining L1 norm with total variation operator.Because the model of solving compound regularizer is more complicated,the operator splitting technique is used to solve the problem of compound regularizer,which is in order to lower the complexity of the solving model,and puts forward a reconstruction method which is iterative weighted.The observation matrix is optimized,according to the priori statistical properties of imaging,which is under different transformations. Simulation results show that this image reconstruction algorithm not only enhances the reconstruction accuracy,but also decreases the time for the reconstruction.
Compressed Sensing(CS);iterative weighted;Magnetic Resonance Imaging(MRI);total variation L1 compression;operator splitting
袁 静.基于压缩感知的核磁共振成像重构算法[J].计算机工程,2015,41(10):270-274.
英文引用格式:Yuan Jing.Magnetic Resonance Imaging Reconstruction Algorithm Based on Compressed Sensing[J]. Computer Engineering,2015,41(10):270-274.
1000-3428(2015)10-0270-05
A
TP301.6
国家自然科学基金资助项目(61372122);宿迁市科技创新专项基金资助项目(Z201209)。
袁 静(1979-),女,讲师、硕士,主研方向:信号处理。
2014-09-17
2014-10-31E-mail:yuanxiaojing1979@163.com

