基于MPA与静态预估的最坏执行时间分析方法

李军义，李 双，张 焱，李仁发

（1.湖南大学信息科学与工程学院，长沙 411000；2.湖南省嵌入式与网络计算重点实验室，长沙 411000）

基于MPA与静态预估的最坏执行时间分析方法

李军义1，2，李 双1，2，张 焱1，2，李仁发1，2

（1.湖南大学信息科学与工程学院，长沙 411000；2.湖南省嵌入式与网络计算重点实验室，长沙 411000）

针对现有嵌入式系统最坏执行时间（WCET）的静态分析方法效率低下问题，利用最小传播算法对程序流进行分析，获得程序中每一个基本块的最小树约束，通过象征性循环上界约束对所求函数中的内部循环变量进行再次约束，并结合最小树约束获得程序的WCET表达式。使用静态预估分析方法对每一个基本块的底层指令周期进行绝对估值，将底层指令周期代入WCET表达式计算出程序最终的WCET值。实验结果表明，与基于程序控制流程图的程序执行时间静态分析方法相比，该方法在保证程序分析精度的同时，大幅提高了分析效率。

嵌入式软件；实时性；最坏执行时间；最小传播算法；静态预估分析

DO I：10.3969/j.issn.1000-3428.2015.10.015

1 概述

嵌入式软件的实时性指标是保证软件安全性和可靠性的重要标准，因此，嵌入式软件对程序的执行时间有着严格要求。对任务执行有严格的时间约束，不允许任何延时的系统称为硬实时系统，可以容许任务在一定范围内的延时称为软实时系统。一般而言，最坏执行时间（Worst-case Execution Time， WCET）分析都是针对硬实时系统。WCET分析是指计算给定应用程序代码片段执行时间的上限，这里代码片段执行时间定义为执行代码片段所花费的处理器时间。

在大部分工业生产中，通常使用一种首尾相连的测试方法来预估程序代码片执行时间的上界和下界，这种方法通常被称为动态时序分析。在该研究领域，同时还存在一种通过分析程序流信息和处理

器特性来预估程序执行时间的方法，这种方法称为静态方法。动态方法主要通过点对点的测试获取程序的WCET值，动态测试方法普遍会低估程序的WCET值。而静态方法由于能通过静态分析获取程序保守的WCET上界，成为研究领域的主流方法，但静态分析方法会高估程序的WCET值。一般而言，静态分析方法高估程序WCET值的程度与通过程序流分析和底层分析获得的约束表达式数量成反比。WCET测试静态方法通过程序路径分析和底层建模，获取程序的安全时间上界。静态方法的计算过程一般分为3个步骤：程序流分析，底层分析以及计算。

本文采用静态分析方法对程序进行WCET估值，利用MPA算法对程序流进行分析，得到程序每个节点的最大执行次数，并由底层分析得出对应节点的最坏执行时间，由此得到程序的WCET值。

2 相关研究

程序流分析的研究对象是程序的源代码，首先通过抽象解释对程序语义进行分析，寻找程序状态不变节点，例如变量 χ的取值在3～5之间。抽象分析方法不需要精确知道整个程序的执行节点，文献［1］提出一种基于抽象解释的点阵模型，该模型用程序流图对程序语义进行分析，简化分析过程，在允许结果不严格精确的条件下，提高分析效率。文献［2-3］分别采用数值域分析和节点线性近似值分析来抽象程序节点的关系。文献［4］提出一种新的分析方法：一致性分析，该方法可用于数值向量化，发现节点的特殊属性。当程序较复杂时，程序通常会产生依赖于另一个节点的约束，例如 P节点的变量χ在节点q处取值小于2y，这种复杂约束称为多面体域，文献［5-6］提出了对多面体域的分析方法。通过对程序源代码执行路径的分析，结合抽象解释，产生类似于程序流图（Program Flow Graph，PFG）的节点流图。程序流分析的目的主要是获得节点之间的约束关系图，然后通过 PIP（Parametric Integer（Linear）Programming）方法［7］对约束进行线性化。PIP方法在一段时间内是程序流分析的主要方法，具有代表性的分析工具是Pip lib［8］工具。但在最小传播算法（Minimum Propagation Algorithm，MPA）［9］提出后，由于MPA算法具有较低的时间复杂度和分析代价，成为替代PIP分析方法的常用方法。

底层分析在程序流分析的基础上，分析每一个节点运行的机器时间上界。底层分析可以通过对每个节点进行机器指令分析获得。因为对计算机底层cache结构、处理器结构和流水线结构分析能获得更多的约束方程，所以底层分析逐渐成为WCET分析的一个全新领域。但是底层分析获得的约束和反馈必须和程序流分析中的节点约束相结合，才能精确程序的WCET上界。

文献［10］通过对指令cache的分析，结合CCG（Cache Conflict Graph）产生约束方程。产生的约束方程通过节点入口、出口在程序流分析的接口进行合并，产生更加精确的时间上界。文献［11］通过分析每一个节点在处理器中的状态，来获得更多的线性约束。理论上cache分析技术可以使静态分析误差精确到2%～2.5%，但是，当对较大或较复杂程序进行分析时，对每一条语句进行复杂分析会使静态分析变得异常繁琐。同时，当程序块较小时，函数调用过程中上下文切换时间、中断时间会产生更多的时间开销，因此，底层分析不能太过复杂。文献［12-13］对不同共享总线进行分析，但是它们都没有与管道、程序路径分析相结合，并且分析过程都是基于体系结构简单的时间异常自由体系。在底层分析方法中，还存在一种将抽象解释和共享总线、指令 cache相结合的方法［14］，但是目前还不能确定将该方法应用于多核处理器和共享总线中是否稳定。为增加研究人员对多核系统的研究，文献［15］提出可预测多核体系，文献［16］提出代码转换的可预测运行模型。但是这 2种方法都不能查找WCET高估的代码源。文献［17-18］对共享总线或cache单独建模，但并未和程序分支以及处理器体系相结合。综上所述，在多核 WCET分析中，对微型体系组件进行建模分析的研究进展缓慢。静态预估分析技术［19］将程序的中间语言作为底层分析节点，其产生的汇编语言能和MPA算法中的节点边相对应，所以，本文使用静态预估分析方法对程序进行底层分析。

3 WCET分析方法

本节将简要介绍MPA算法的运算过程，同时给出WCET分析过程中基本块的定义以及MPA算法运算过程中的条件简化规则，最后介绍基于静态预估分析获取底层指令周期的新方法。

3.1 MPA算法模型

文献［5］介绍了基于参数WCET分析方法，文献［9］更加详细地介绍该方法的分析步骤。参数分析方法使用式（1）对程序的WCET值进行计算：

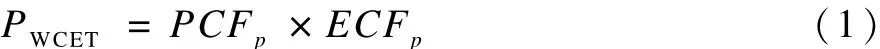
其中，PCFP是对程序进行程序流分析和底层分析后得到的节点函数；ECFP为该程序节点底层机器周期的最大执行次数，ECFP的计算过程和PCFP相似。通过式（1）便能计算出程序的 WCET值。

其中，cq是程序节点的WCET值；Pq是程序节点执行次数的上界。使用式（2）能够计算得到程序流分析的节点函数。MPA算法使用基本块分析法，将具有相同机器周期的语句或若干语句定义成基本块，得到 PCFL=λP0，P1，P2，…，Pn，其中，n是基本块的个数。由于静态预估分析方法并不要求每个基本块机器周期相同，因此本文方法将基本块定义如下：

定义1（顺接） 对于任意语句或基本块i，j，如果i运行之后必定会运行j，则有Statementi和Statementj存在顺接关系，且Statementi是Statementj的前顺接，定义为Pre（Statementj）=Statementi。Statementj是Statementi的后顺接，定义为suc（Statementi）=Statementj。

定义2（基本块） 基本块 Bi，j可以由有限条语句组成，并且任意基本块运行结束状态唯一，不存在2种不同的运行结束状态。

定义3（组合块） 如果存在 Pre（Bi，n）=Bm，n，并且eχecute1（Bi，n）=eχecute2（Bi，n）=…=eχecuten（Bi，n），则基本块Bi，n为由Bi，j和 Bm，n，组合成的新基本块，称为组合块。如果2个基本块能组成组合块，用组合块的WCET值替代组成组合块的原模块的WCET值能提高测试效率，简化测试过程。

如果某行是跳转语句或者分支语句，则它不能和其他基本块形成组合块。因为如果它是组合块，将与定义2矛盾。

定理（MPA简化） 在使用MPA算法获取节点χm约束的过程中，如果 χm的约束条件 χm≤χk，且对于所有的χk≤χa+χb，存在a=m或b=m，则条件χk≤χa+χb可以省略。

证明：因为当存在约束条件χm≤χk时，m已经加入队列 conteχt，当遇到 χk≤χa+χb时，因为队列由于使用PIP算法计算WCET值的时间复杂度较大，甚至存在计算瓶颈，而MPA算法时间复杂度较小，自动化程度较高，因此现在研究领域大多使用M PA算法替换PIP算法。MPA算法计算PCFP公式如下：conteχt和集合｛a，b｝交集不为空，χk≤χa+χb被过滤，等价于条件χk≤χa+χb被去除，得证。

3.2 基于静态预估分析的底层指令周期获取

MPA算法和PIP算法都是基于参数的WCET计算方法，为了计算程序的WCET，ECFP值必须经过底层分析获得。随着处理器的运算速度加快，处理器的运算结构越来越复杂，目前还没有工具能对代码运行过程中流水线、处理器的变化作出精确的估计。对每一条语句进行繁琐的流水线分析将会严重影响程序WCET值的分析速度。特别是对较大程序进行WCET分析时，过度注重处理器细节将会使程序的静态分析过程工程量巨大。所以，本文将采用程序底层指令周期静态预估分析技术对程序进行底层分析。该方法在某种程度上忽略流水线结构，无论是多流水线处理器还是单流水线处理器，都使用单流水线估计代码块的WCET值。该计算方法具有快捷准确的优点，虽然对于多核、多流水线的处理器将会产生一定的高估，但这种高估并不会产生较大的影响。

静态预估可视化分析方法通过分析中间代码段与源程序中语句的对应关系，提取和计算CPU周期数。该方法将程序的分析过程分为3层：可视化分析层，源代码分析层和汇编代码分析层。可视化分析层的分析过程类似于程序流分析，通过分析程序流，获得程序基本块的树形结构。但是可视化分析过程并没有使用象征性上界预估、PIP方法或MPA方法获得程序流的严谨约束，存在不足。而MPA算法具有自动计算，时间复杂度较低等优点，本文方法使用MPA算法代替可视化分析过程进行顶层分析。源代码分析层是代码底层分析的过度阶段，通过对树形结构进行分析，获取代码基本块。汇编代码分析层最终将基本块编译成底层汇编代码。通过计算基本块的机器指令周期，获得程序的每个基本块的机器指令周期值。

4 基于MPA和静态预估的WCET分析方法

4.1 WCET分析方法

本文方法综合MPA算法和静态预估可视化分析技术，测试流程如图1所示。首先使用MPA算法对程序进行分析，获得程序的数据流约束。然后在获得数据流约束的基础上，查看是否存在文献［20］中提到的6种特殊循环，如果存在，则使用循环上界约束增加约束。最后使用经过处理之后的约束和底层分析后获得的指令周期获取程序最终的WCET值。

图1 WCET方法的测试流程

4.2 基于WCET方法的测试程序

基于WCET方法的测试程序具体如下：

上述测试程序L中函数fun的功能是计算整形二维矩阵a中m行～n行元素的和，本文将展示如何通过WCET方法测试该函数的WCET值。

本文对该程序进行程序流分析，得到如图2所示的程序节点图。程序的每一个代码节点都有相应的参数容量，定义该参数容量为 P0，P1，…，P8，由图2的分析可以得到程序的约束关系：

图2 测试程序L的程序节点

通过MPA算法对χ0，χ1，…，χ8节点构造MPA树，然后计算节点的 MPA值（构造过程参考文献［5］），得到所有节点的M in-Tree值tq为：

该程序的WCET值定义如式（3）所示：

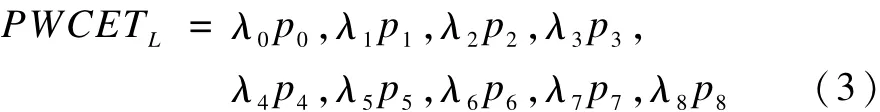
其中，λn表示基本块 n的机器周期，λn值需要通过静态预估分析获取。

MPA算法在计算 P0，P1，…，P8的过程中，最终获得的是基于输入参数表示的函数。对于图2中函数内部循环控制变量j，使用文献［20］中的6个基本样例中的意外终止循环获得循环上界：

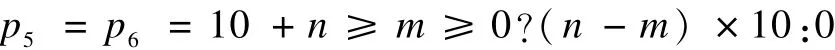
得到如下简化结果：

其中，λ0，λ1，…，λ8为相应代码块的机器指令指令周期，需要通过底层分析获得。本文方法使用静态预估可视化分析方法进行底层分析。式（3）中的 λ0，λ1，…，λ8可以通过源代码分析和汇编代码分析获得，从而计算出程序的WCET值。

底层分析代码1具体如下：

底层分析代码2具体如下：

上面2段底层分析代码展示了使用本文方法进行指令分析的处理过程。其中，代码1是在代码编译成底层汇编代码之后 P5的底层分析代码。可以看出，编号为10的代码与编号为12的代码之间的部分恰好等价于 MPA算法 P5边的值 λ5。这为MPA算法在该方法中进行程序流分析提供了良好的契合点。通过对代码1进行指令分析可以得到λ5的值。而代码 2则是图 2中 P7，P8，P2指令周期代码。以此类推，还可以得到 λ0，λ1，…，λ8汇编指令周期值，从而得到 λ0，λ1，…，λ8结果集。

程序最终PWCET化简为：

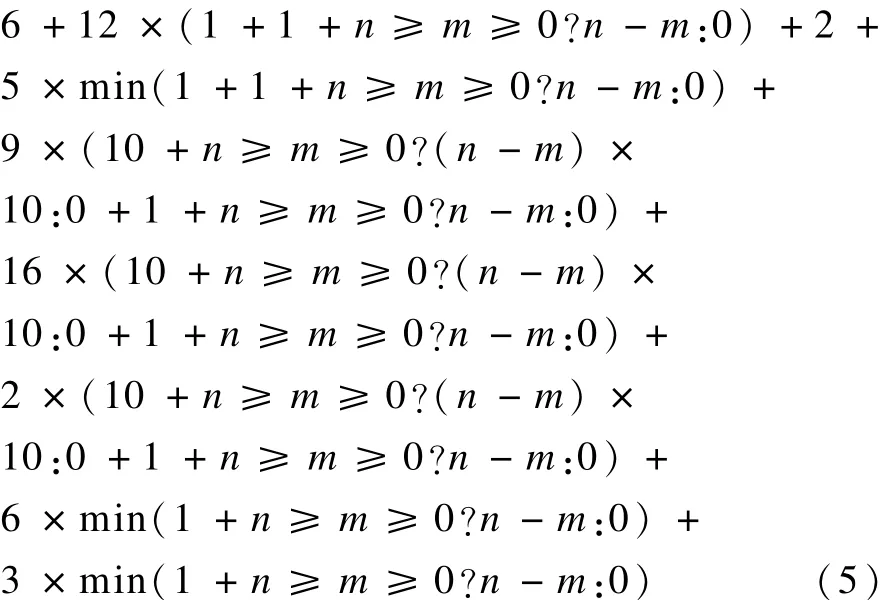
由于调用函数进行入栈和出栈操作运行11+ 19个指令周期，因此最后调用函数 fun的指令周期值为：

（1）当n＜m时，PWCETL=384；

（2）当nm≥0时，PWCETL=378+323（n-m）。

假如fun函数在晶振为10 MHz、1个机器周期由6个状态周期组成的处理器中运行并被调用，则运行fun（1，4）的最坏执行时间为1.608 m s。同样使用基于控制流程图的可视化时间分析方法获得的运行时间为 1.488 ms，由此可见，本文方法计算的WCET值结果比原方法计算出的WCET值高。分析其原因主要有：（1）MPA算法虽然减少了算法时间复杂度，提高结果精确性，但是由于MPA算法主要根据程序节点关系进行递归，因此会产生一定的高估。如测试程序L中，当取m=n时，本文方法分析结果为384，而实际情况是357，因为MPA算法根据路径节点关系多计算了一次 P4，P5，P6。 （2）本文方法使用文献［20］获得循环上界，在保证WCET安全性的同时，提高了WCET的估计值。

5 实验与结果分析

Malardalen基准程序中的duff，expint，fac，ludcmp，recursion 5个程序能较直观地反映基准程序WCET值与程序的循环次数、递归次数、程序执行路径的关系，因此选择这 5个程序通过控制参数分别分析其WCET值，将这些程序在晶振为10 MHz、1个机器周期由6个状态周期组成的处理器中运行并被调用。

表1是本文方法与基于程序控制流程图的程序执行时间静态分析方法［19］的对比，第1列是基准程序名称，第2列是基准程序中与WCET值相关的参数值，第3列数据表示文献［19］方法得出的WCET值，第4列本文方法测试得出的WCET值，第5列表示2种方法测试WCET的差异值，第6列是2种方法得到的WCET差值相对于文献［19］方法的高估百分比。

表1 2类方法的预估WCET值对比

由表1可知，本文方法对比于文献［19］方法测试的WCET值略高，当程序非常简单，程序节点很少的情况下，2种方法测试得到的WCET值差异比较大，但差异值依然在合理范围内。但随着程序节点的增多，程序复杂度增大，差异值越来越小，趋近于0，由此可见，本文方法对大型复杂程序测试的值很稳定。但是使用MPA算法替换程序控制流程图的方法，与底层分析相结合，在大型复杂程序中更具适应性，并且大大减轻了手工分析的复杂与低效性，使高层源代码层语句时间分析向自动化测试方向更前进了一步。

6 结束语

本文提出一种基于MPA和静态预估的WCET分析方法。该方法使用MPA算法改进静态预估可视化分析，对原静态预估分析方法的中间代码进行分析，将程序底层汇编代码同MPA算法中边节点对应，然后结合象征性上界约束对顶层程序流中特殊循环结构进行分析，获得最终精确的WCET值。该方法较好地契合了WCET分析领域底层分析与程序流解析脱节的研究现状，为顶层分析技术与先进底层分析技术的高效整合提供了借鉴。本文通过实例展示了新方法的分析过程，并与基于程序控制流程图的程序执行时间静态分析方法的测试结果进行对比。虽然本文方法的测试结果会产生一定的高估，但由于引入M PA算法进行自动化测试，相比于手工测试方法有很大的改进。随着处理器技术的发展，底层处理器结构越来越复杂，下一步工作将主要以底层分析为主，提高WECT分析的效率及精确度。

［1］ Cousot P，Cousot R C P，Cousot R.Abstract Interpretation：A Unified Lattice Model for Static Analysis of Program s by Construction or Approximation of Fixpoints［C］//Proceedings of the 4th ACM Symposium on Principles of Programming Languages. New York，USA：ACM Press，1977：238-252.

［2］ MinéA.The Octagon Abstract Domain［J］.Higher Order Symbolically Computing，2006，19（1）：31-67.

［3］ Cousot P，Halbwachs N.Automatic Discovery of Linear Roximation of Fixpoints［C］//Proceedings of the 5th ACM Symposium on Principles of Programming Languages.New York，USA：ACM Press，1978：84-97.

［4］ Philippe G.Static Analysis of Arithmetical Congruences［J］.International Journal of Computer Mathematics，1989，30（3/4）：165-199.

［5］ Lisper B.Fully Automatic Parametric Worst-case Execution Time Analysis［C］//Proceedings of the 3rd International Workshop on Worst-case Execution Tim e Analysis.Washington D.C.，USA：IEEE Press，2003：77-80.

［6］ Bygde S.Static WCET Analysis Based on Abstract Interpretation and Counting of Elements［EB/OL］.（2010-03-15）.http：//www.mrtc.mdh.se/index.php？choice=publications&id=2144.

［7］ Feautrier P.Parametric Integer Programming［J］. Operations Research，1988，22（3）：243-268.

［8］ Piplib Website［EB/OL］.（2009-11-07）.http：//www. piplib.org/.

［9］ Stefan B，Andreas E，Björn L.An Efficient Algorithm for Parametric WCET Calculation［J］.Journal of System s Architecture，2011，57（6）：614-624.

［10］ Li Y T S，Malik S，Wolfe A.Performance Estimation of Embedded Software with Instruction Cache Modeling［J］.ACM Transactions on Design Automation of Electronic System s，1999，4（3）：257-279.

［11］ Chattopadhyay S，Kee C L，Roychoudhury A，et al.A Unified WCET Analysis Framework for Multi-core Platforms［C］//Proceedings of the 18th IEEE International Real-time and Em bedded Technology and Applications Symposium.Washington D.C.，USA：IEEE Press，2012：319-329.

［12］ Rosen J.Bus Access Optimization for Predictable Implementation of Real-time Applications on Multiprocessor System s-on-chip［C］//Proceedings of the 28th IEEE International Real-time Systems Symposium. Washington D.C.，USA：IEEE Press，2007.

［13］ Chattopadhyay S，Roychoudhury A，Mitra T.Modeling Shared Cache and Bus in Multi Core Platforms for Timing Analysis［C］//Proceedings of SCOPES’10. Washington D.C.，USA：IEEE Press，2010：99-108.

［14］ Lv Mingsong.Combining Abstract Interpretation with Model Checking for Timing Analysis of Multicore Software［C］//Proceedings of the 31st Real-time Systems Symposium.Washington D.C.，USA：IEEE Press，2010：339-349.

［15］ Marco P.Hardware Support for WCET Analysis of Hard Real-time Multicore Systems［C］//Proceedings of the 36th Annual International Symposium on Computer Architecture.New York，USA：ACM Press，2009.

［16］ Pellizzoni R.A Predictable Execution Model for COTS-based Em bedded System s［C］//Proceedings of the 17th Real-time and Em bedded Technology and Applications Symposium.Washington D.C.，USA：IEEE Press，2011：269-279.

［17］ Yan Jun，Zhang Wei.WCET Analysis for Multi-core Processors with Shared L2 Instruction Caches［C］// Proceedings of RTAS’08.W ashington D.C.，USA：IEEE Press，2008：80-89.

［18］ Li Yan.Timing Analysis of Concurrent Program s Running on Shared Cache Multi-cores［C］//Proceedings of RTSS’09.Washington D.C.，USA：IEEE Press，2009：57-67.

［19］ 孙昌爱，金茂忠，刘 超.程序执行时间的静态预估与可视化分析方法［J］.软件学报，2004，4（1）：69-75.

［20］ Knoop J，Kovács L，Zwirchmayr J.Symbolic Loop Bound Computation for WCET Analysis［M］.Berlin，Germany：Springer，2012.

编辑 陆燕菲

Worst-case Execution Time Analysis Method Based on MPA and Static Prediction

LI Junyi1，2，LI Shuang1，2，ZHANG Yan1，2，LI Renfa1，2
（1.College of Information Science and Engineering，Hunan University，Changsha 411000，China；2.Key Laboratory for Em bedded and Network Computing of Hunan Province，Changsha 411000，China）

Aiming at the problem of low efficiency for embedded system Worst-case Execution Time（WCET）static analysis methods，this paper uses Minimum Propagation Algorithm（MPA）to analyze the program flow and obtain the m in-tree of each code block.Then it gets more strict constraints through the analysis of inner loop variables of function by symbolic loop bounds computation，and gets a WCET expression through constraints of m in-tree and the loop bounds. Finally，it uses static prediction method to solve the WCET by absolute valuation of underlying instruction cycle of each basic block，and calculates the final WCET value.Experimental results show that this method increases the analysis efficiency as well as ensures accuracy com pared with program execution time static analysis method based on process control flow diagram.

embedded software；real-time；Worst-case Execution Time（WCET）；Minimum Propagation Algorithm（MPA）；static prediction analysis

李军义，李 双，张 焱，等.基于 MPA与静态预估的最坏执行时间分析方法［J］.计算机工程，2015，41（10）：76-82.

英文引用格式：Li Junyi，Li Shuang，Zhang Yan，et al.Worst-case Execution Time Analysis Method Based on MPA and Static Prediction［J］.Computer Engineering，2015，41（10）：76-82.

1000-3428（2015）10-0076-07

A

TP393

广东省产学研合作重大专项基金资助项目（2012-391）。

李军义（1970-），男，副教授、博士，主研方向：嵌入式软件，软件测试；李 双、张 焱，硕士研究生；李仁发，教授、博士生导师。

2014-09-28

2014-11-23E-mail：junyilee@hnu.edu.cn