基于车—梁耦合的吊车组合模型研究★

蔡 越 欧洪禹 段圣刚

(1.武汉理工大学土木工程与建筑学院，湖北 武汉 430070； 2.武汉中央商务区建设投资股份有限公司，湖北 武汉 430000)

〗。

〗

φi(x)

φi(ξ)

=diag{mi}+Mdiag{φi(ξ)[Φ(]ξ)〗}。

=2vMdiag{φi(ξ)[Φ′](ξ)〗}。

{φi(ξ)}[Φ″(ξ)〗。

{P}=(Pe+Mg){φ1(ξ)，φ2(ξ)，…，φN(ξ)}T。



基于车—梁耦合的吊车组合模型研究★

蔡 越1欧洪禹2段圣刚1

(1.武汉理工大学土木工程与建筑学院，湖北 武汉 430070； 2.武汉中央商务区建设投资股份有限公司，湖北 武汉 430000)

针对车—梁耦合系统动力响应分析，提出并推导了吊重摆动力与移动激励组合模型以考虑吊重运行产生的摆动力及吊车与吊车梁的耦合关系，并通过MATLAB求解得吊车运行过程中吊车梁所受激励，以此作为输入荷载，利用有限元计算分析吊车梁的动力响应并与实际工程实测数据进行对比分析，表明该模型是合理可行的，可应用于吊车动力响应分析。

组合模型，车—梁耦合，移动激励，拉格朗日，动力响应

0 引言

随着城镇化建设的深入，城市人口不断增加，城市交通拥堵成为日益突出的问题。地铁轨道交通因其准时、安全、运量大、效率高及环境污染小等优点逐渐成为城市轨道交通建设重要工程。如图1所示，地铁+物业的综合开发模式已蔚然成风。地铁车辆段上盖物业的开发是提高城市土地利用率和地铁投资回报率的有效途径，具有广阔的应用前景，然而由此产生的振动舒适度问题成为制约其发展和推广的瓶颈。

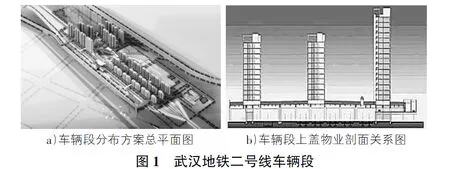
目前关于地铁上方地表建筑物振动研究较多，而涉及吊车动荷载引起的上部结构振动的研究则鲜有见诸文献，主要是由于地铁+物业的综合模式出现时间不长且吊车荷载的模拟方法不够完善，因此，建立合理的吊车动荷载计算模型进而开展关于吊车引起的振动舒适度问题的研究，具有一定的工程参考价值。

1 荷载模型

本文重点研究吊车的动荷载计算模型。吊车计算模型通常有移动力、移动质量两种模型，如图2所示模型优点在于计算简便，便于推广。但是由于简化过程中忽略了吊重摆动力的影响，计算结果与实际数据有较大出入。

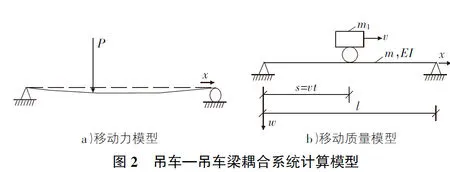
近几年，基于Kamal等人对吊重摆动控制的研究成果，国内引入了吊重摆动力模型，考虑了吊重摆动引起的摆动力，并验证了模型的可行性。但是，模型的预设条件是吊车梁刚度不变，未考虑吊车与梁的耦合效应。而实际工况吊车梁具有一定刚度，吊车运行过程中会产生变形。由此，导致了计算数据与实测数据的偏差。

而在吊重摆动力模型基础上深入考虑吊车与吊车梁耦合关系时，计算得系统的运动微分方程是(N+1)元二阶非线性时变微分方程组，编程过程中难以克服方程组非线性与时变性的特点，不便运算及推广。就此，本文提出吊重摆动力与移动激励组合模型，以考虑吊重摆动力影响以及吊车与吊车梁的耦合关系。如图3所示，组合模型包括吊重摆动力模型及移动激励模型，首先利用吊重摆动力模型计算吊重引起的摆动力，继而将摆动力等效为吊车荷载输入，采用移动激励模型计算吊车梁实际所受激励。区别于一般移动质量、移动力模型，本文采用的移动激励模型，由移动质量与作用其上的荷载共同构成吊车梁所受激励。

计算吊重引起的摆动力时，采用吊重摆动力模型。如图4所示为吊重摆动力的空间计算模型。由于吊车吊重运行时吊车梁变形较小，对于吊重摆动工况影响极小，基本不影响吊重摆动力的结果。故此，吊重摆动力模型求解过程中忽略吊车梁变形对吊重摆动力的影响。

假设：考虑小车不动仅大车沿吊车梁运行的工况，大车及小车为一刚体。

条件：大车及小车质量为M；轨道梁的抗弯刚度为EI，吊重质量为m；吊绳在铅垂方向静平衡时长度为l；吊绳的拉伸刚度为k；小车停在桥架跨中，大车运行方向为x方向。设吊绳与铅垂方向夹角为α；吊绳水平投影与x方向夹角为γ；吊绳长度变化量为δ；小车所在位置为(xM,0,0)，xM为关于t的函数。

由上可知该系统具有δ，α，γ三个自由度。

吊重坐标：

(1)

系统总动能：

(2)

系统的总势能：

(3)

拉格朗日运动方程：

(4)

对广义坐标δ，α，γ应用拉格朗日方程，有：

(5)

以上方程为高阶非线性微分方程组，解析解的求解几乎不可能，故编程对式(5)进行数值求解。相关计算参数：大车及小车总质量为M=24 000 kg，吊重质量为m=367 kg，轨道梁抗弯刚度EI=1.72×1011N/m2，重力加速度g=9.8 m/s2，吊绳在铅垂方向静平衡时长度为l=5 m，吊绳的拉伸刚度为k=1×106N/m。吊车保持0.55 m/s的速度匀速运行。由MATLAB求解微分方程组，可得δ时程曲线，进而由吊绳拉伸系数计算得吊重摆动力时程曲线，见图5。

由摆动力时程曲线可知，吊车运行过程中产生的摆动力随时间变化不定。摆动力对吊车梁的激励并非吊车运行过程中吊车梁实际所受全部外界激励，还有吊车运行过程中吊车对吊车梁的激励，因此求解吊车运行过程中吊车梁所受荷载激励需要进一步分析计算。本文采取将吊重引起的摆动力等效为随吊车移动的荷载，以移动激励模型为计算模型，进行吊车梁动力响应分析。

如图3b)所示，移动质量为大车及小车质量M，等效移动荷载为Pe，梁的单位长度质量为m，在梁上以速度v匀速运动。简支梁各参数：跨度为l，抗弯刚度为EI，ξ=vt。

移动激励模型作如下假定：1)梁的特性用Euler-Bernulli梁理论来描述；2)吊车运行过程中吊车与梁始终保持接触。

根据梁的振动理论，其动力学方程如下：

δ为Dirac函数，由于y是极小量，梁的柯氏力、向心力以及梁的阻尼影响很小均可以忽略不计，从而梁的振动方程简化为：

(6)

(7)

(8)

(9)

改写成矩阵形式：

(10)

其中：

=diag{mi}+Mdiag{φi(ξ)[Φ(]ξ)〗}。

=2vMdiag{φi(ξ)[Φ′](ξ)〗}。

{P}=(Pe+Mg){φ1(ξ)，φ2(ξ)，…，φN(ξ)}T。

其中，[Φ(]ξ)〗为模态函数矩阵；[Φ′](ξ)〗，[Φ″(ξ)〗分别为[Φ(]ξ)〗关于ξ的一阶和二阶导数矩阵。

方程(10)为二阶参数激励时变微分方程组，,,,均随时间t及运动参数v而变化，采用Newmark逐步积分可以求得各个时刻的q(t)再代入式(7)即可求得任意时刻梁上任意点的挠度。积分求解过程可借助MATLAB编程实现。已知梁上任意位置挠度时程曲线即可导入数据进行有限元模拟吊车运行过程吊车梁所受激励。

2 吊车梁有限元模型

计算长度取3个柱距长度，吊车梁上铺设吊车轨道，吊车直接作用于轨道上。车轮始终保持与梁接触，吊车梁与柱子、下翼缘与牛腿之间连接采用高强螺栓连接；上翼缘在单侧与柱子连接，约束其水平向线位移。另外，此模型是从整个吊车梁中截取的三段来进行计算分析，所以在分析时还应考虑整段梁对模型两端面的约束作用，故此，建模时约束了两个端面的线位移。轨道梁最终的有限元计算模型如图6所示。

ANSYS与MATLAB之间相互调用数据，求解吊车运行时吊车梁跨中加速度响应。

3 工程实例

3.1 工程概况

常青花园车辆段是武汉地铁2号线的车辆段，也是2号线最主要的车辆检修基地和停放基地，车辆段预留有上盖物业开发条件。满足本课题的研究条件，故此，本文以常青花园车辆段作为实例与理论分析作为对比。

测试工况：测试时，选用联合车库中吊车匀速行驶的一种工况进行分析，单程运行共4次即来回2次，运行间距大致为3个～4个柱距，具体情况如表1所示。

表1 测试工况

测点布置：吊车梁支座处及吊车运行的吊车梁上各布置1个测点，每个测点放置1个传感器，记录铅垂向的加速度时程。其中，吊车梁的测点在吊车梁跨中。

3.2 测试结果及分析

传感器对应测试吊车运行速度为0.55 m/s，0.60 m/s,0.66 m/s时 吊车梁跨中及支座处加速度数据见表2。

表2 吊车梁跨中及支座处加速度峰值

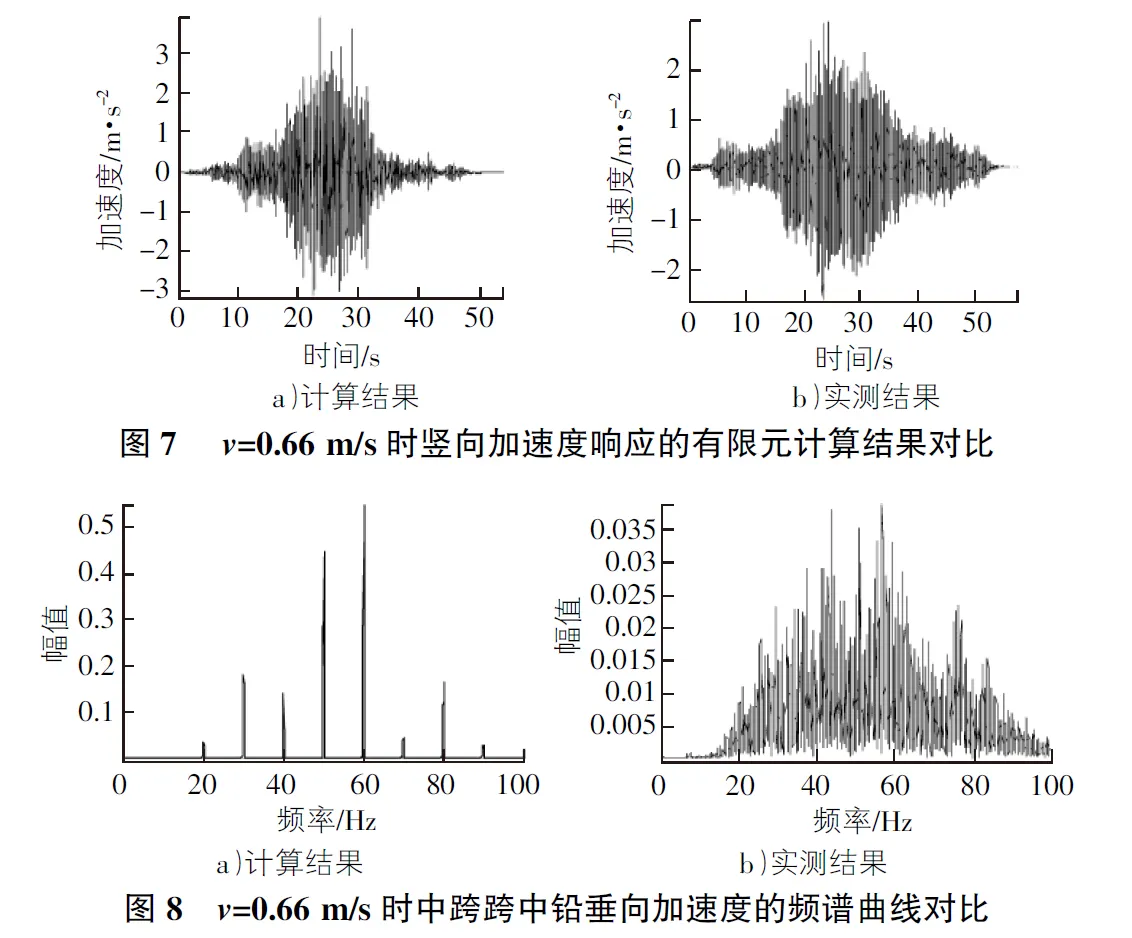
图7为v=0.66 m/s时吊车梁竖向加速度响应的有限元计算结果与实测结果。通过MATLAB fft()函数进行快速傅立叶变换，频谱图分析，得到0.66 m/s时跨中及支座处加速度频谱图8，图9。

由图7～图9可见：梁跨中加速度响应有限元计算结果与实测数据在变化规律和幅值上吻合较好，计算值的频谱成分没有实测值丰富，但计算结果频谱图的卓越频率与实测基本吻合。从而验证了本文所采用的荷载模型及吊车梁模型是合理的，即本文采用的吊车动荷载模拟方法是可行的。

然而由数据对比分析可知，理论计算数据与实测数据之间仍有一定出入，其主要原因为：1)吊车的简化处理，忽略了轮轴内部的相互作用；2)未考虑轨道不平顺的影响。

4 结语

本文详细推导了吊重摆动力及移动激励组合模型以考虑吊车吊重运行产生的摆动力及吊车与吊车梁的耦合关系，并由MATLAB编程求解吊车梁所受激励。通过ANSYS与MATLAB间数据调用，计算得吊车梁动力响应并与工程实测数据进行对比分析。结果表明采用该组合模型得到的吊车梁动力响应与实测数据基本吻合，表明该模型是合理可行的，可应用于吊车动力响应分析。

[1]彭 颖.吊车荷载作用下地铁上盖物业振动舒适度和噪声研究.武汉：武汉理工大学，2012.

[2]Kamal A.F.Moustafa1， A.M Ebeid.Nonlinear Modeling and Control of Overhead Crane Load Sway.Transactions of the ASME Journal of dynamic Systems,Measurement and Control,1988(110):266-271.

[3]马博军,方勇纯,刘先恩,等.三维桥式吊车建模与仿真平台设计.系统仿真学报，2009，21(12)：3798-3803.

[4]周玉娟,黄 金,何 卫,等.吊车动荷载计算模型研究.中国水运，2014,12(14):130-132.

[5]Michaltsos G T,Kounadis A N.The effects of centripetal and coriolis forces on the dynamic response of lightbridges under moving loads.J.of Vibration and Control,2001(7):315-326.

[6]张 涛.常青花园车辆段上盖物业开发设计方案研究.山西建筑，2013，39(16)：25-27.

Research on the crane combination model based on vehicle-beam coupling★

Cai Yue1Ou Hongyu2Duan Shenggang1

(1.CivilEngineeringandArchitectureCollege,WuhanUniversityofTechnology,Wuhan430070,China;2.WuhanCentralBusinessDistrictConstructionInvestmentLimitedCompanybyShare,Wuhan430000,China)

According to the vehicle-beam coupling system dynamic response analysis, this paper proposed and deduced the carrying swing power and mobile incentive combination model to consider the coupling relationship of swing power caused by carrying operation and crane and crane beam, and through MATLAB solved the vehicle-beam incentive in crane operation process, taking this as the input load, used the finite element calculated and analyzed the dynamic response of crane beam and compared with actual engineering measured data, indicating that the model was reasonable and feasible, could apply to the crane dynamic response analysis.

combination model, vehicle-beam coupling, mobile data, Lagrange, dynamic response

1009-6825(2015)18-0163-03

2015-04-14★：武汉市城建科研项目(项目编号：611400621)

蔡 越(1991- )，男，在读硕士; 欧洪禹(1977- )，男，高级工程师; 段圣刚(1990- )，男,在读硕士

TU323.1

A