斜拉桥拱塔大缩尺比模型试验研究

胡 成， 汪 莲， 周 安， 王静峰， 邵亚会， 吴节松

（1.合肥工业大学 土木与水利工程学院，安徽 合肥 230009；2.土木工程结构与材料安徽省重点实验室，安徽 合肥 230009）

多塔斜拉桥在国内发展较晚，相关报道也较少。混凝土拱形桥塔多塔斜拉桥的桥塔造型新颖，美学效果好，但桥塔刚度问题、结构力学性能等问题的研究亟待解决。进行新型索塔结构的模型试验是解决该问题的重要途径之一。现有的桥塔节段模型试验一般采用与实桥相同的建筑材料，如混凝土强度等级、钢筋布置及大小。从1999年至今，国内二十多项工程曾开展过索塔锚固区节段模型试验，大部分模型为足尺模型，即1∶1，也有少数试验采用1∶1.5或1∶1.6的大缩尺比模型［1－10］，如南京长江二桥、鄱阳湖口大桥桥塔锚固区足尺节段模型试验、芜湖长江大桥桥塔锚固区足尺节段模型试验、漳州战备大桥的索塔鞍座节段模型试验、润扬大桥北汊斜拉桥桥塔锚固区足尺节段模型试验等。目前国内外斜拉桥模型试验研究主要是小尺寸全桥模型试验或索塔锚固区足尺节段模型试验。马鞍山长江公路大桥右汊斜拉桥索塔结构整体模型试验，采用1∶10大尺寸缩尺比例，与原模型相同的混凝土材料强度。由于试验规模较大，目前该类研究较少见，仅有甬江特大桥的双联索塔结构整体模型试验研究报道，但其模型的缩尺比较小，为1∶40。

目前国内外对拱型索塔结构大比例整体模型试验、设计理论和施工监控研究尚不多见。多塔斜拉桥结构性能和安全性的研究对于我国大型桥梁的建设和健康发展都具有十分重要的意义。

1 工程概况

马鞍山长江公路大桥位于安徽省马鞍山市，连接马鞍山和巢湖两市。大桥全长35.9km，其中右汊为2×260m三塔拱塔斜拉桥，跨径布置如图1所示。

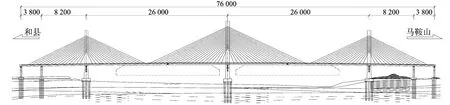
图1 拱塔斜拉桥结构布置图

采用拱形索塔使其在斜拉索作用下处于三维空间复杂受力状态，且索塔锚固区本身构造和受力性能也甚为复杂，桥梁设计时单纯依靠力学模型的理论分析难以全面反映拱塔结构的实际工作性状。因此，在拱塔施工前有必要采用缩尺模型试验辅以理论分析的手段对索塔结构及其锚固区的实际工作性能进行研究，以期对索塔结构的设计优化和施工工艺及控制提供依据和指导。本文主要介绍马鞍山长江大桥右叉斜拉桥拱塔1∶10模型试验的设计及研究成果，试验模型如图2所示。

图2 1∶10拱塔结构试验模型

2 试验模型设计

为满足试验精度和对拱塔施工有指导意义等要求，试验模型采用预应力钢筋混凝土结构，同时模型设计按等应变原则进行模拟，即模型的基本断面形式与实际结构相同，主要结构尺寸按照几何相似的原则进行模拟。试验模型中普通钢筋的设计按照含筋率相等的原则进行；模型中拉索力的布置采用力等效原则进行，即相应工况下，模型张拉索力产生的拱塔控制截面的内力应与实际拱塔控制截面的内力满足相似比的要求。模型试验考察了拱塔整体结构的空间受力特征，并研究了在施工阶段和运营阶段塔柱关键部位、塔柱与横梁连接部位的应力分布状况。

2.1 模型相似比

模型试验的相似理论采用一定比例的试验模型，通过相似比的关系推算原结构的力学状况［11］。根据模型的比例确定相似比以及相应换算关系显得尤为重要。考虑到模型制作的方便、试验场地、试验设备条件等多种因素，拱塔模型结构采用相同材料、缩尺比例1∶10的试验模型，并遵守相似理论原则。

相应的相似比为：

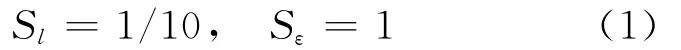
因为试验模型和原模型采用同种材料，则有：

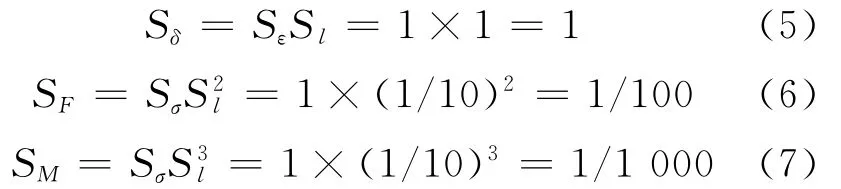
由以上分析可知，在采用与原型结构相同材料的情况下，弹性模量、泊松比的相似常数为1，模型几何尺寸按照相似比1∶10进行缩尺，则材料的容重相似常数Sr为10，即模型材料的容重应为原型材料的10倍。因此在试验中需首先对拱塔模型进行恒载补偿，尽可能将9倍模型自重的附加荷载均匀施加在整个拱塔上。

拱塔是拱塔整体试验模型的上部结构，包括塔柱和横梁。其中，塔柱的代表性断面有5个，横梁的代表性断面有3个。塔柱截面最大尺寸为0.81m×0.76m，可用螺杆较长的12.9级直径16mm高强螺栓来模拟精轧螺纹预应力粗钢筋；横梁截面宽度为4.227m，可用直径φs15.24mm的高钢筋强度低松弛钢绞线来模拟精轧螺纹预应力粗钢筋。

2.2 加载系统

本试验规模较大，加载系统复杂，在斜拉索张拉前需考虑拱塔模型的恒载补偿、横梁支座反力模拟及塔柱横向预应力等效等结构的恒载状态。

2.2.1 恒载补偿

本试验的荷载补偿示意图如图3所示。

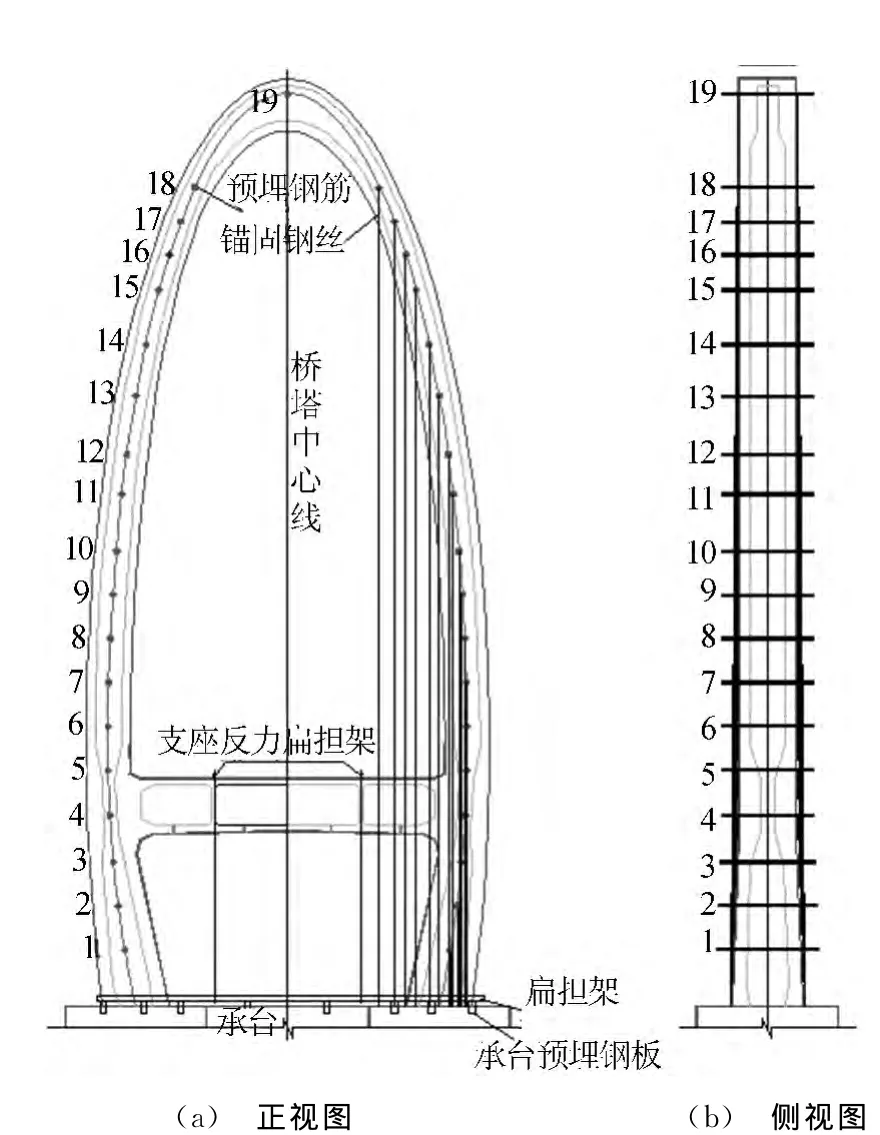
图3 本文荷载补偿示意图

在设计试验模型时，结合斜拉索的位置和可操作的实际空间，将拱塔沿高度方向共分为19个部分，在每个部分的每肢塔柱中点处施加相当于该节段自重9倍的补偿恒载，每个节段的配重沿桥跨方向对称加载在塔柱壁上。国内学者曾提出利用杠杆原理、悬臂钢块等方法解决配重技术难题，即在各节段塔壁中心处通过预埋φ40钢棒伸出塔壁（沿桥垮方向）建立支点，在该支点上搁置工字型钢（I10），型钢短臂端用锚固在台座上的钢绞线拉住，同时用吊机将事先浇筑好的混凝土块吊装于型钢的长臂端形成杠杆，从而可以用小质量的配重块达到补偿恒载的要求，每个预制配重块的质量为31～127kg。但是该方案有较大安全隐患问题，同时需要制作较多的钢块，费用高，配重荷载精度难以控制。

针对配重技术难题，本文提出一个有创新性的配重加载方案：在靠近塔脚处的承台上预埋几块钢板，以预埋的钢板为基础在塔脚周围焊接张拉配重拉索用的台座。在各节段塔壁中心处预埋φ32高强钢棒伸出塔壁（沿桥垮方向），并用拉索联结伸出塔壁的钢棒和钢结构台座，通过在台座处使用扭矩扳手调节拉索索力以达到配重要求。通过计算，每个配重拉索的索力为7.88～38.92kN。由于配重的拉索可能会与模型结构的斜拉索在竖向出现位置重叠，此时可以将配重拉索的竖直角度进行微小调节以避开模型结构斜拉索，调整角度后的配重拉索应该对相应的索力进行调整，索力的调整应按照塔柱对称以保证索力的竖直分力不变的原则进行。

在靠近塔脚处的混凝土承台上预埋钢板，以预埋的钢板为基础在塔脚周围焊接张拉配重拉索用的型钢台座（反力架）；同时在各节段塔壁中心处预埋φ32高强钢棒伸出塔壁（沿桥垮方向），并用拉索联结伸出塔壁的钢棒和型钢台座，通过在台座处使用扭矩扳手来调节拉索索力以达到配重目的，扭矩扳手的扭矩系数通过配置在钢筋拉杆锚固端的穿心式传感器进行标定和校核。

2.2.2 横梁支座反力及塔柱横向预应力

考虑到实际拱塔结构的横梁上有支座反力，故需在拱塔横梁上施加2个对称的竖向集中荷载，模拟横梁支座反力。试验中，支座反力通过在每个加载点设置扁担梁，采用与恒载补偿类似的加载方式进行张拉及调整，具体如图4所示。采用预埋高强螺杆模拟塔柱横向预应力，试验过程中，通过扭矩扳手对高强螺杆施加预应力，达到对拉索锚固区施加横向预应力的目的。塔柱横向预应力需对称加载，同时通过设置在高强螺杆锚固端的穿心式传感器进行标定与校核。

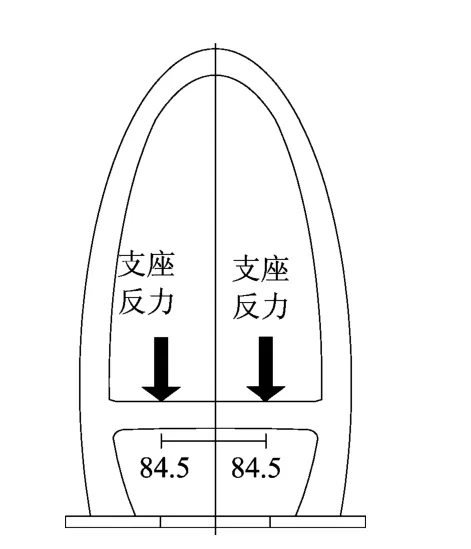
图4 横梁支座反力加载图

2.2.3 斜拉索索力

试验通过张拉斜拉索钢绞线进行加载，根据加载力的不同来模拟桥梁施工及运营中的不同荷载工况。本研究的荷载工况包括最大悬臂施工状态、二次调索施工状态、正常使用极限状态、承载能力极限状态以及1.2倍承载能力极限状态。索力张拉值通过千斤顶的油压表控制，并采用穿心式压力传感器和索力测试仪配合进行测试校核。

3 试验工况及内容

马鞍山长江大桥右汊斜拉桥拱塔结构模型试验共进行了以下11个工况试验：① 工况0，为桥塔模型未进行塔身预应力钢筋张拉及配重，处于自然状态；② 工况1－1，为塔柱横向预应力张拉50%；③ 工况1－2，为塔柱横向预应力张拉100%；④ 工况2，为横梁预应力张拉；⑤ 工况3，为塔柱预应力张拉和配重张拉；⑥工况4，为横梁支反力第1次施加（对应施工阶段的最大悬臂阶段）；⑦ 工况5，为施工阶段最大悬臂状态（分批次进行拉索张拉）；⑧ 工况6，为施工阶段2次调索阶段；⑨ 工况7，为正常使用极限状态；⑩ 工况8，为承载能力极限状态；○11 工况9，为1.2倍承载能极限状态。

在模型试验中，本文对拱塔结构关键部位进行应力测试和变形观测，测试内容主要有：

（1）在模型浇筑前埋设钢筋应变片进行索塔关键截面的纵向受力钢筋应变测试。

（2）在混凝土表面粘贴无线应变计进行索塔关键截面的混凝土应变测试。

（3）在索塔表面布设全站仪棱镜观测点和千分表以便测量索塔关键部位的变形。

（4）张拉前对千斤顶进行标定，张拉过程中借助千斤顶的油压表来控制，同时利用穿心式压力传感器和索力测试仪进行索力测试和校核。

（5）在拱塔混凝土表面进行裂缝观测，用裂缝观测仪和放大镜观测每级荷载下有无裂缝展开，以及各工况下的裂缝分布和宽度，并绘出裂缝分布图。

4 试验结果与分析

以最大悬臂施工阶段为例，工况5的索力测试值和设计值如图5所示。因油压千斤顶的灵敏工作区间有限，模型试验取值较小的拉索索力的相对误差控制在15%以内，由图5可以看出，索力实测值和设计值吻合较好，表明拱塔模型结构试验加载方式可行。

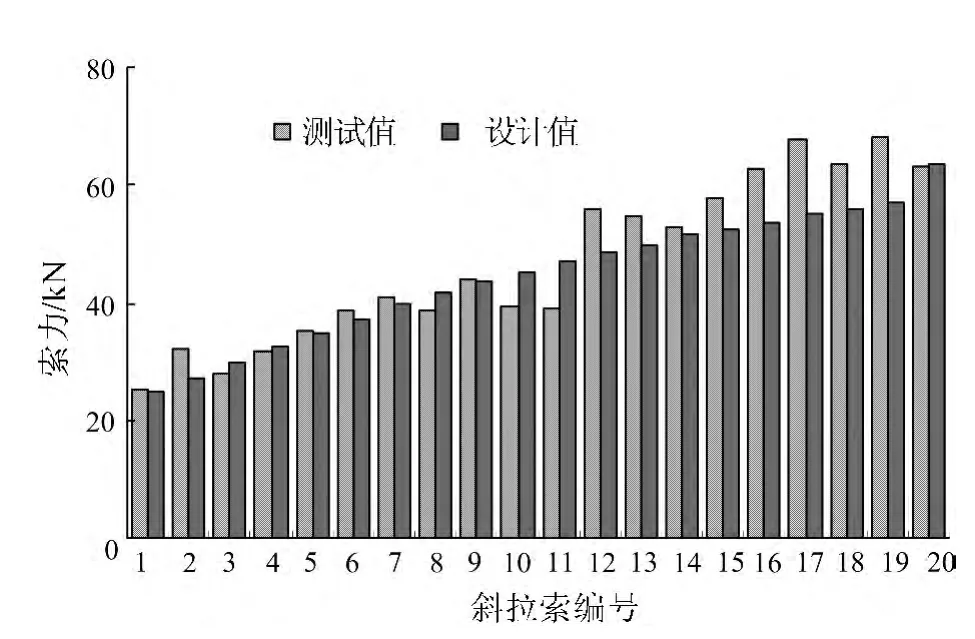
图5 东南方向索力测试值和试验设计值

工况5时3－3截面（塔底上1.8m处的塔肢横截面）各混凝土表面测点的应变实测值和计算值如图6所示。大部分测点应变数据测试值误差较小，应变实测值与计算值吻合较好。3－3截面处于全截面受压状态，图6中的少许拉应变均为拱塔混凝土表面横向应变。3－3截面法向应变范围 为 （－10～－250）×10－6，正 应 力 值 范 围 为－0.30～－7.60MPa。

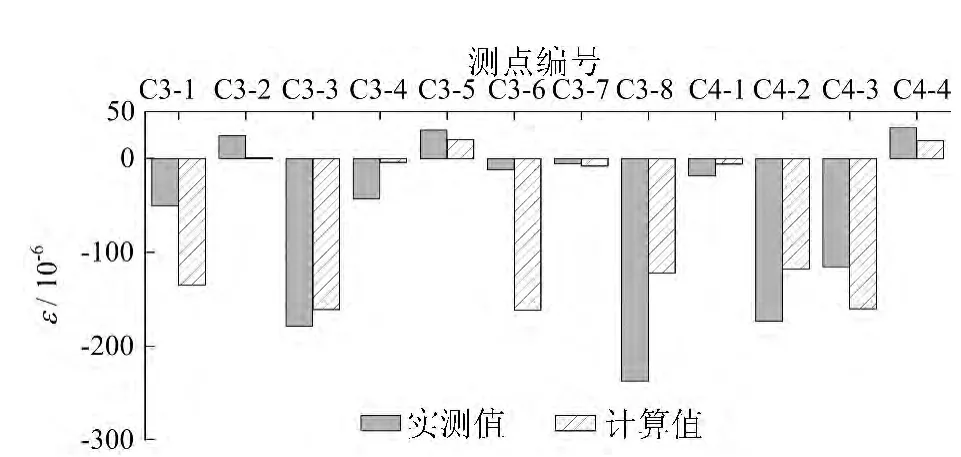
图6 3－3截面表面混凝土测点应变实测值与计算值

工况5下各截面钢筋测点的应变实测值与有限元计算值如图7所示。塔柱上距塔底1.80m处的3－3处于全截面受压状态。3－3截面钢筋测点的应变范围为（－76～－325）×10－6，相应应力范围为－14.82～－63.38MPa，有限元理论计算的应变范围为（－68～－259）×10－6，应力范围为－13.26～－50.51MPa。

工况5时的索力张拉完成后，在距塔底8m处的两塔柱顺桥向内侧相同位置出现横向、纵向裂缝，具体裂缝情况如图8所示。在后续试验工况中，裂缝在长度及宽度上并未出现新的发展。

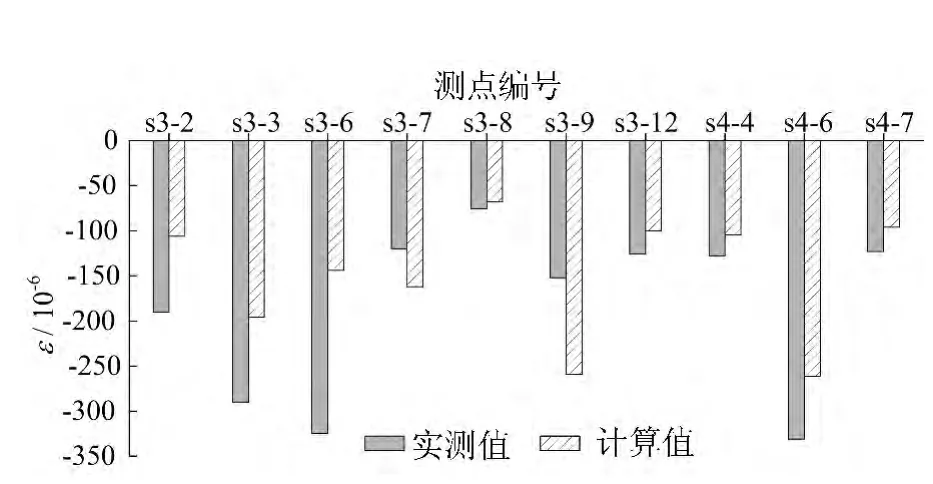
图7 3－3截面钢筋测点应变测试值与有限元计算值

图8 南塔柱8m处内侧壁裂缝分布

有限元数值模拟研究表明，在该区域的局部部位出现较小拉应力主要是由于精轧螺纹钢锚固区的局部应力集中，由此带来的较小范围内的混凝土和钢筋受拉。工况5下的弯矩图如图9所示。

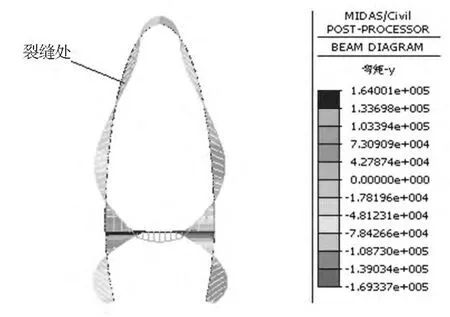
图9 拱塔在最大悬臂施工状态下弯矩图

图9表明，试验中混凝土裂缝出现的区域正好位于塔柱内侧弯矩较大处，即模型高度距离塔底为7.2～10.0m。由此看出，塔柱在该高度范围内受力较为薄弱，需进行结构及配筋优化。

为验证拉索锚固区高强螺栓形成的环向紧箍力对塔柱混凝土开裂的影响，本文选定横桥向C18（距离塔底9m左右）拉索出口点上侧2根高强螺栓未施加轴向力。该工况结束后在该塔柱横桥向的两侧壁上发现裂缝，如图10所示。且随着后续工况索力的增加，裂缝的宽度及长度进一步增长。试验表明，拱塔横向预应力的施工质量对其结构安全意义重大，精轧螺纹钢筋的预应力张拉及压浆施工的质量需严格控制。

图10 北塔柱西侧壁裂缝分布

5 结 论

本文结合马鞍山长江公路大桥右汊斜拉桥的特点，为解决拱塔结构设计和施工的关键技术难题，进行了拱塔结构大缩尺比整体模型试验研究。试验得出以下结论：

（1）本试验用千斤顶油压表、穿心式传感器和索力测试仪来相互验证索力张拉值，斜拉索索力实测值与设计值的误差范围除个别较大外，大多数均控制在15%以内，测试结果表明索力实测值和设计值吻合较好，同时证实了拱塔结构试验的索力加载方案可行，加载精确度高。

（2）试验设计的恒载补偿是通过张拉配重拉杆对各节段的预埋钢棒施加压力荷载，达到配重的目的。试验反映了拱塔结构在各施工工况下的受力及变形性能，数值模拟分析也表明试验较好地体现了拱塔结构的工作性能。

（3）模型试验结果表明，除个别测试点位误差较大外，基于本研究模型设计和试验方法的模型试验结果（混凝土和钢筋微应变）与ANSYS有限元数值模拟的结果误差在15%以内。

（4）塔体高度为7.2～10.0m（实桥高度为72～100m）范围内塔柱较为薄弱，在结构优化及施工质量控制时应予以特别注意。

马鞍山长江大桥模型试验设计合理，较好地再现了拱塔结构的受力性能，对该桥施工过程的控制有很好的指导作用，同时模型试验验证了分析计算方法的正确性，弥补了理论计算过程中因模型简化所造成的误差，可为类似桥塔模型试验提供设计经验和技术指导。

［1］ 项贻强，陈国强.鄱阳湖口大桥索塔节段足尺模型试验与分析研究［J］.中国公路学报，2000，13（4）：74－77.

［2］ 戴 捷，张喜刚，吴国民.苏通大桥主桥索塔设计［C］／／中国公路学会桥梁和结构工程分会2004年全国桥梁学术会议论文集，2004：47－53.

［3］ 中交公路规划设计院.杭州湾跨海大桥工程设计［R］.北京：中交公路规划设计院，2003.

［4］ 中交公路规划设计院.苏通大桥主桥技术设计专题报告：索塔锚固区方案比选和设计［R］.北京：中交公路规划设计院，2004.

［5］ 万 臻，李 乔.大跨度斜拉桥索梁锚固区三维有限元仿真分析［J］.中国铁道科学，2006，27（2）：41－45.

［6］ 合乐中国有限公司.杭州湾跨海大桥北航道通航孔桥索塔锚固区的结构分析［R］.上海：合乐中国有限公司，2006.

［7］ 刘兆丰，赵人达，杨永清.广珠线西江特大桥主桥索塔锚固区局部应力分析［J］.中外公路，2012，28（4）：122－125.

［8］ 乔建东，刘桂林.紫金斜拉桥索塔锚固段足尺模型试验研究［J］.铁道标准设计，2008（11）：54－57.

［9］ 姚建军，刘孝辉，李 琦，等.忠县长江大桥索塔锚固区模型试验与裂纹预测［J］.桥梁建设，2009（2）：32－39.

［10］ 刘兆丰，孟 鑫，赵人达，等.长寿长江公路大桥索塔节段足尺模型试验研究［J］.公路交通科技，2009，26（8）：77－83.

［11］ 方诗圣，胡 成，吴文清，等.微混凝土模型材料基本性能试验研究［J］.合肥工业大学学报：自然科学版，1999，22（5）：76－79.