玄武岩纤维自密实混凝土流变性能研究

卢 睿， 朱大勇， 詹炳根

（1.合肥工业大学 交通运输工程学院，安徽 合肥 230009；2.土木工程结构与材料安徽省重点实验室，安徽 合肥 230009；3.合肥工业大学 土木与水利工程学院，安徽 合肥 230009）

0 引 言

自密 实 混 凝 土 （self－consolidating concrete，SCC），又称为自流平混凝土、高流动混凝土，是通过掺入高效减水剂得到的流动性极好的混凝土，可不经振捣靠自重流平、充满模板、包裹钢筋，达到密实。这一新型材料有良好的力学性能和耐久性，能解决传统混凝土施工中钢筋密集难以振捣、钢筋和预埋件振捣移位等问题［1］。纤维自密实混凝土是一种特殊的高性能混凝土，它的流动性较高且具有适中的黏度。其工作度的影响因素不仅与水胶比和高效减水剂有关，而且受纤维类型、纤维掺量和骨料性质等影响明显。要完整准确地掌握新拌自密实混凝土复杂的工作性，必须从SCC流变学机理和模型入手，只有这样才能较好揭示混凝土中各成分的相互作用以及新拌SCC工作性的机理，从而建立混凝土拌合物的流变性能与实际工程应用中工作性参数的关系曲线或者关系式，实现现场施工控制与应用。从流变学角度对新拌纤维自密实混凝土的研究，对其屈服应力和塑性黏度参数的有效测定，是掌握和控制混凝土工作性的一个关键，开辟了一条研究其工作性的很好途径［2－4］。

1 流变模型

E.C.Bingham等最早提出了应用于瓷土、硅藻土等材料的宾汉姆体（Bingham body），并用屈服应力和塑性黏度这2个参数来表征材料的性质，这2个参数满足（1）式，即

其中，τ为外力产生的剪应力；τ0为初始流动屈服应力；η为塑性黏度；为剪切应变速率。在各种流变模型中，通常Bingham模型被视为描述新拌SCC流变性的最适合的模型，它概念清晰、物理意义明确。

本文按照图1所示的思路，应用Bingham模型，以Tresca屈服准则为依据，通过微积分的方法将坍落度桶中新拌混凝土分层，每层限制在2个平行薄板内，只考虑新拌混凝土的内部层流，从而建立关于纤维自密实混凝土流动速度和坍落流动直径的微分方程，推导得到屈服应力和坍落流动度的关系，同时利用坍落时间T500计算拌合物的平均黏度，以此来反应塑性黏度的大小［5］。

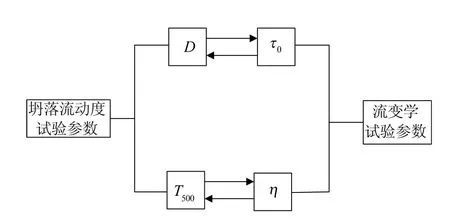
图1 坍落流动度试验参数与流变学试验参数之间的关系

新拌自密实混凝土的坍落流动和混凝土重力产生的压应力，如图2所示。

假设坍落流动度试验的过程中混凝土保持为截锥体形状，并且新拌混凝土不可压缩，H、Rt和Rb分别为坍落度桶高度、顶部半径和底部半径，h、rt和rb分别为坍落混凝土的高度、顶部半径和底部半径。

将重力方向记为z，以向上为正，取距截锥体底部高度为z的隔离体，其中dz、rz、pz分别为混凝土隔离体厚度、半径和压应力［6］。

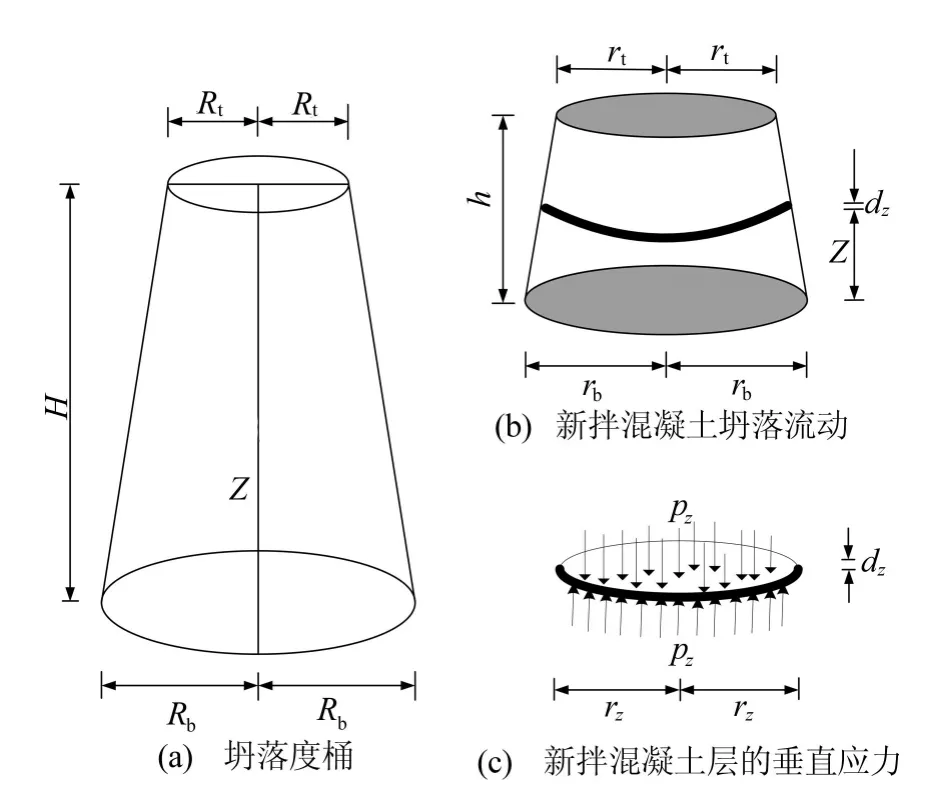
图2 新拌自密实混凝土的坍落流动和混凝土重力产生的压应力

由坍落流动时边界条件可知，当z＝h时，rz＝rt，v＝0；当z＝0时，rz＝rb。仅考虑混凝土截锥体最底层的流动，在z＝0～h的范围内对（1）式进行积分可得坍落流动速度方程式为：

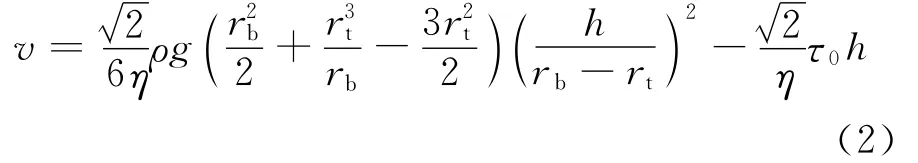
当试样停止坍落流动时，v＝0，由（2）式可得：

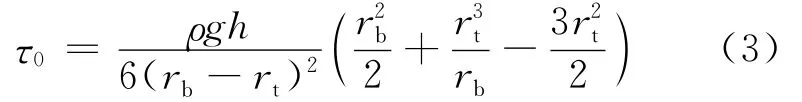
（3）式中rb＝D／2，通过多次试验验证，可得玄武岩纤维自密实混凝土的坍落流动度中rt＝1.0rb。因此（3）式表达了屈服应力τ0与坍落流动直径D之间的转换关系。

考虑流动速度v与z轴的方向余弦，可得平均流动速度表达式为：

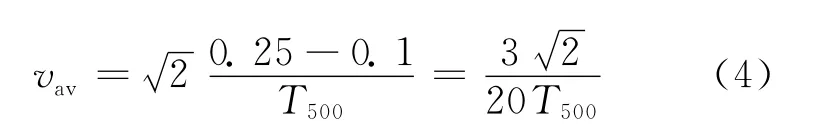
令v＝vav，由（2）式可得平均黏度表达式：

其中，τ0由（3）式计算。这样就利用试验所得的D和T500求得了自密实混凝土的屈服应力和塑性黏度，方便在施工现场快速、准确地判断自密实混凝土的工作度。

2 试 验

为了验证玄武岩纤维自密实混凝土流变性能符合Bingham模型，同时得到满足玄武岩纤维自密实混凝土的流变性能，试验在C45自密实混凝土中掺加长度分别为5、12、24mm，体积分数分别为0、0.1%、0.2%、0.3%的短切玄武岩纤维，测试坍落拓展度参数D及T500，将其代入Bingham模型中求解纤维自密实混凝土的屈服应力及塑性黏度，同时得到最佳掺量下的流变性能。

2.1 原材料

试验用原材料为：P·O 42.5普通硅酸盐水泥；合肥东兴产F级粉煤灰；霍山Ⅱ级洁净中砂，细度模数2.3；巢湖散兵碎石，5～20mm连续级配；安徽梦谷纤维材料科技有限公司生产的短切玄武岩纤维，其性能指标见表1所列；江苏苏博特新材料股份有限公司生产的PCA－Ⅰ聚羧酸高效减水剂，减水率为27%。

表1 玄武岩纤维的物理力学性能指标

2.2 混凝土配合比

本试验根据文献［7］的有关规定，通过对胶凝材料用量、粉煤灰掺量、砂率、减水剂用量等影响自密实混凝土工作性的因素进行系统的试验分析［8－9］，经优化，采用绝对体积法配制出 C45玄武岩纤维自密实混凝土的工作性能满足自密实性能等级为三级的要求，砂率为0.486，水胶比为0.38，粉煤灰替代量为30%，基准减水剂用量为粉体质量的1.51%。随着纤维掺量和纤维长度的增加，混凝土的流动性降低，为了保证混凝土依然能够达到自密实的效果，增加一定减水剂，最后通过多次试验得到流变性能良好的玄武岩纤维自密实混凝土配合比，其中，水泥、粉煤灰、砂、石、水的 用 量 分 别 为 331.8、142.2、793.8、838.9、180.0kg／m3，减水剂用量和纤维掺量见表2所列。玄武岩纤维体积掺量为0、0.1%、0.2%、0.3%，纤维长度为5、12、24mm，相应的编号为A－0－0、A－5－0.1、A－5－0.2、A－5－0.3、A－12－0.1、A－12－0.2、 A－12－0.3、 A－24－0.1、 A－24－0.2、A－24－0.3。

表2 自密实混凝土中减水剂用量和纤维掺量

2.3 纤维混凝土制备方法

先将玄武岩纤维与砂、石混合干拌1min，之后将全部用水量的1／2加入搅拌机内至搅拌均匀，再将水泥和粉煤灰加入搅拌1min后将剩余的水和减水剂加入再搅拌3min。使纤维与骨料均匀混合，最大限度地避免混凝土拌合物结团和泌水［10］。

2.4 纤维自密实混凝土的工作性

判断混凝土拌和物流动性好坏及观察分析判定混凝土拌和物的抗离析能力最为直观的方法是观察新拌纤维自密实混凝土的坍落扩展过程。从流变力学的角度看，扩展速度的快慢反映了混凝土拌合物黏度的高低。坍落扩展度试验是将新拌混凝土装满坍落度筒，平稳提起坍落度筒，测试坍落度筒提起后混凝土流动至500mm刻度圈所用的时间T500和混凝土流动稳定后的最终扩展度D。坍落扩展度D和流动时间T500反映了新拌自密实混凝土的流动能力及塑性屈服能力。通过试验测得坍落流动度参数D和T500见表3所列。

表3 纤维自密实混凝土坍落流动度试验结果

2.5 试验结果分析

对于相同配合比的基体混凝土，随着玄武岩纤维体积掺量的增加，玄武岩纤维自密实混凝土坍落流动度随之下降。当加入体积分数为0.2%的短切玄武岩纤维时，混凝土坍落流动度迅速下降；纤维体积掺量达到0.3%时混凝土的坍落流动变得缓慢，黏度变大，随着短切玄武岩纤维长度的增大，玄武岩纤维自密实混凝土坍落流动度呈下降趋势，如图3所示。相对于纤维体积掺量对自密实混凝土坍落扩展度的影响，纤维长度的影响相对较小。

对于相同配合比的基准混凝土，随着短切玄武岩纤维体积掺量和长度的增加，玄武岩纤维自密实混凝土坍落流动时间呈升高趋势，且满足三级自密实混凝土的要求，如图4所示。

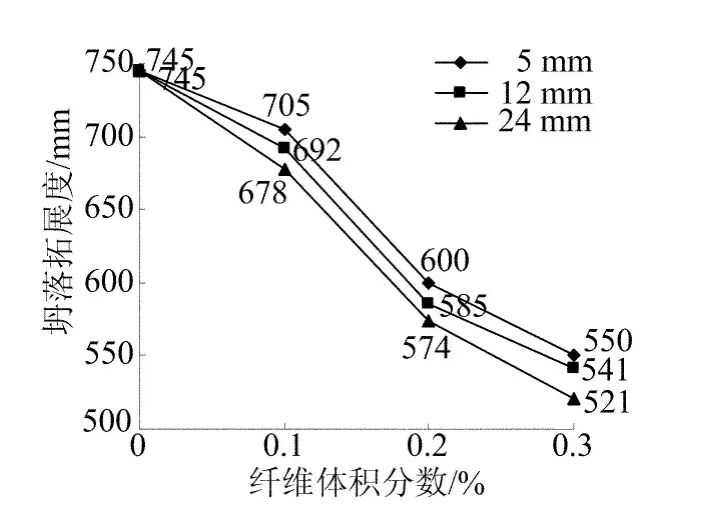
图3 纤维掺量及长度与坍落扩展度的关系

图4 纤维掺量及长度与流动时间T500的关系

3 模型计算

3.1 计算屈服应力和平均黏度

以表2所列玄武岩纤维自密实混凝土为例计算屈服应力。将实测的 A－0－0～A－24－0.3自密实混凝土的坍落流动度D带入（3）式，计算得到10种拌合物发生坍落流动时的屈服应力，如图5所示（图中横轴的编号省略了“A－”）。由图5可知拌合物屈服应力随坍落流动直径的减少而增加。

将计算得到的 A－0－0～A－24－0.3的屈服应力τ0以及实测的10种玄武岩纤维自密实混凝土拌合物坍落流动时间T500代入（5）式，计算可得拌合物平均黏度ηav，如图6所示（图中横轴的编号省略了“A－”）。由图6可知平均黏度随拌合物流动时间的增加而增加。

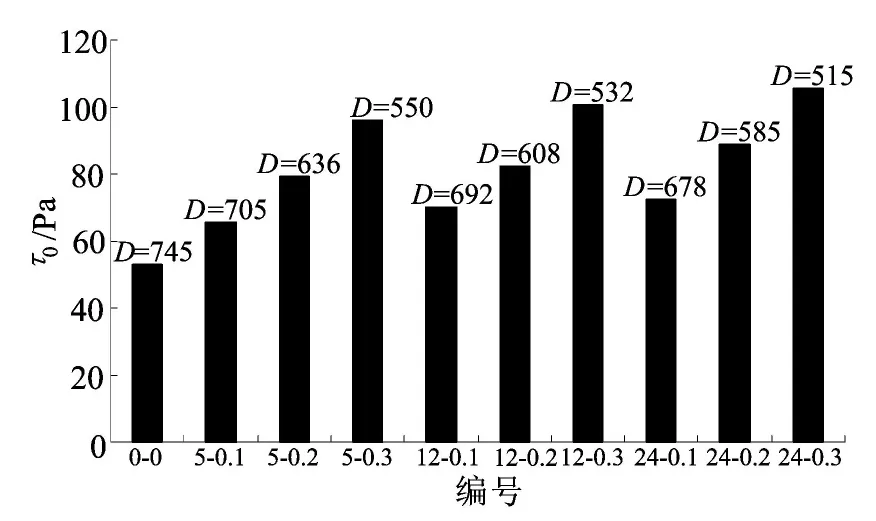
图5 玄武岩纤维自密实混凝土屈服应力计算结果

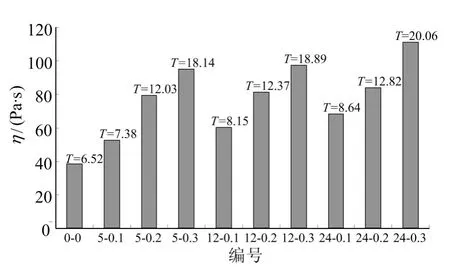
图6 玄武岩纤维自密实混凝土平均黏度计算结果

3.2 计算结果分析

Banfill对文献可查水泥浆体、砂浆、自密实混凝土和普通混凝土流变学参数屈服应力τ0和塑性黏度η进行了总结分析，结果如图7、图8所示［11］。

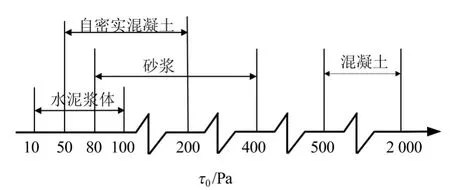
图7 水泥浆体、砂浆、自密实混凝土和普通混凝土屈服应力范围

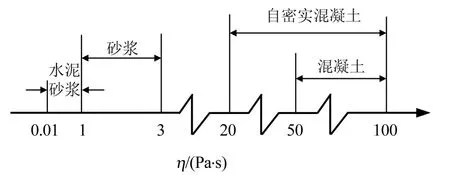
图8 水泥浆体、砂浆、自密实混凝土和普通混凝土塑性黏度范围

图7表明自密实混凝土的屈服应力τ0数值在（50～200）Pa范围内，用（3）式计算的τ0值在（52～105）Pa范围内，如图5所示。因此利用本文建立的流变模型计算玄武岩纤维自密实混凝土屈服应力是适用的，可以作为评判纤维混凝土工作性能好坏的重要参数。

图8表明自密实混凝土塑性黏度η的数值在（20～100）Pa·s范围内，用（5）式计算的平均黏度ηav在（38～111）Pa·s范围内，表明利用本文建立的流变模型计算玄武岩纤维自密实混凝土的塑性黏度只能在一定程度上反映塑性黏度，原因在于Bingham模型没有考虑触变性以及工作性损失，当高效减水剂增加，屈服应力τ0降低，同时掺入粉煤灰使塑性黏度ηav上升，最终导致其黏度范围超出经验范围之外。

4 结 论

（1）坍落流动直径D与屈服应力之间、坍落流动时间T500与黏度之间存在定量关系。使用Bingham模型公式可由坍落流动直径D和坍落流动时间T500分别计算玄武岩纤维自密实混凝土的屈服应力和平均黏度，参数简单，物理意义明确，在玄武岩纤维自密实混凝土现场施工中，具有工程实践指导意义。

（2）新拌玄武岩纤维自密实混凝土坍落流动度试验中，截锥体底层混凝土流动速度是屈服应力、塑性黏度的函数。拌合物坍落流动直径随屈服应力的增加而降低，坍落流动时间T500随平均黏度的增加而增加。在本文中，玄武岩纤维长度为5mm，纤维体积掺量为0.2%时，混凝土流变参数屈服应力和塑性黏度都满足自密实混凝土的要求，流变性能达到最佳。

（3）平均黏度可以反映塑性黏度，但是本模型只能在一定程度上反映塑性黏度，还需要考虑触变性以及工作性损失的影响，因此尚需对模型进一步改进，使其更真实地反映塑性黏度对玄武岩纤维混凝土流变性能的影响。

［1］ 单 智，石建军，熊 恩，等.新拌自密实混凝土流变性研究［J］.混凝土，2010，（11）：108－112.

［2］ 叶 焕.自密实混凝土的流变性能及其对分层浇筑的影响［D］.哈尔滨：哈尔滨工业大学，2013.

［3］ 郑少鹏.基于流变特性的新拌水泥混凝土质量控制技术研究［D］.天津：河北工业大学，2012.

［4］ 潘 雨，巴恒静.流变参数在高性能混凝土研究中的应用［J］.工业建筑，2002，32（9）：57－59.

［5］ 刘思国.纤维自密实混凝土工作性能和抗剪性能研究［D］.大连：大连理工大学，2010.

［6］ Saak A W，Jennings H M，Shah S P.A generalized approach for the determination of yield stress by slump and slump flow［J］.Cement ＆ Concrete Research，2004，34（3）：363－371.

［7］ CECS 203：2006，自密实混凝土应用技术规程［S］.

［8］ 陈一馨，吕彭民，宋绪丁.钢－钢纤维混凝土梁剪力件疲劳性能试验研究［J］.合肥工业大学学报：自然科学版，2013，36（4）：456－460.

［9］ 孙小军，鲍忠城，陈阳利，等.玄武岩纤维增强水泥胶砂韧性性能研究［J］.合肥工业大学学报：自然科学版，2014，37（6）：700－704.

［10］ Brown M C，Ozyildirim C，Duke W L.Investigation of fiber－reinforced self－consolidating concrete，VTRC 10－R8［R］.Alexandria，VA：National Technical Information Service，2010.

［11］ Banfill P F G.The rheology of fresh cement and concrete：a review［C］／／Proceedings of International Congress on the Chemistry of Cement，Durban，South Africa，2003：50－62.