二维瞬态热传导问题热物性参数反演

周焕林， 徐兴盛， 李秀丽， 胡 豪

（合肥工业大学 土木与水利工程学院，安徽 合肥 230009）

在航空航天、冶金铸造、化工制药、材料冶金、机械制造、交通运输、核反应堆、地热能勘探、生物传热、热工测量、土木工程、无损探伤、冷冻储藏等工程领域，热传导反问题是传热学研究的热点之一，它是利用实验手段测得物体内部或边界上某些点的温度、热流及其随时间的变化历程，通过求解导热微分方程来反演物体热通量、材料热传导系数或物体内部热源分布等参数。

随着反演问题理论研究的不断深入，研究者提出了多种求解热传导反问题的方法。文献［1］将材料的热传导系数值按温度区间分段离散，基于遗传算法和伴随方程法通过材料边界点的温度测量来反演各温度区间热传导系数值；文献［2］建立了非线性稳态热传导问题的有限元模型，对非线性热物性和边界条件进行了反演；文献［3］研究了非线性瞬态热传导问题中导热系数和边界条件的多宗量反演；文献［4］基于无网格有限点法反演一维热传导问题的源参数；文献［5］利用直接积分法研究了一维非线性热传导反问题，给出了热传导系数的反演结果；文献［6－7］利用有限差分法与高斯－赛德尔迭代法，研究了一维瞬态热传导问题的热参数；文献［8］采用截断奇异值正则化方法反演二维各向同性弹性力学Cauchy问题的边界条件；文献［9］采用截断奇异值法反演二维各向同性材料Cauchy位势问题的未知边界条件；文献［10］利用基本解法与移动最小二乘法对未知边界上的温度值进行反演计算；文献［11］采用数值积分方法对热通量进行了反演识别，计算过程中使用了未来时刻的温度值；文献［12－13］利用共轭梯度法反演一维非线性瞬态热传导问题中的导热系数和热容量，且进一步反演了二维非均质材料的热传导系数；文献［14］使用复变量求导法计算灵敏度矩阵。

近些年来，非线性反演方法迅猛发展，已经成为反演理论方法的重中之重。非线性反演方法主要有：梯度法、牛顿法、共轭梯度法、蒙特卡洛法、变尺度法、模拟退火法、遗传算法和人工神经网格法等。共轭梯度法是介于梯度法和牛顿法之间的一种有效处理反问题的方法，并且集成了2种方法的优点。共轭梯度法仅仅利用了目标函数的一阶偏导数的信息，既克服了梯度法收敛速度慢的缺点，又省去了牛顿法在每一次搜索时需要重复计算和储存Hessian矩阵并求其逆矩阵的麻烦。并且共轭梯度法还具有收敛性和稳定性高、所占存储空间小、不需要引入外来参数以及具有如牛顿法那样在极小值点附近收敛速度快的优点。

本文基于边界元法反演二维瞬态导热问题的热扩散系数和导热系数，并讨论迭代初值、数据随机偏差等对反演结果的影响。

1 正问题

1.1 导热理论

对于二维非稳态热传导问题，满足方程：

其中，a为热扩散系数；λ为导热系数。

由加权余量法得到二维瞬态导热问题的边界积分方程：

其中

1.2 边界积分方程的离散

首先要对时间域离散，假设函数T、q随时间变化，由于T和q比T＊和q＊的变化要慢得多，由此近似认为在极短的时间段内为常数，则（2）式转变为：

对时间内层求积分得：

其中

其中，C为欧拉常数，C＝0.577 215 66。

将边界Γ划分成N个线性单元，空间域Ω划分成M个四边形单元，则

单元内任意一点的温度或热通量可以由单元端点的值通过线性插值来确定。插值函数为：

整理（9）式可得：

其中

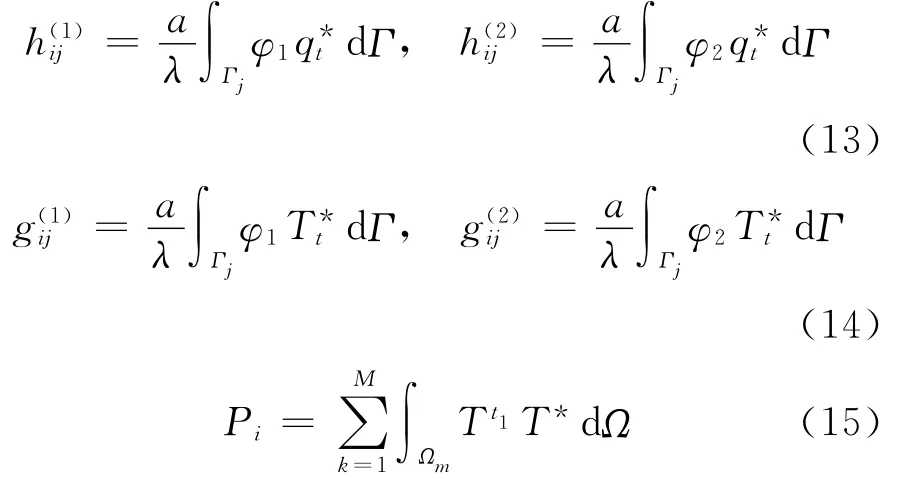
Pi为整个空间Ω上的初始温度对源点i的影响。将（12）式写成矩阵形式为：

其中，H为温度系数矩阵；G为热通量系数矩阵；Tt2为节点温度；Qt2为节点热通量。

引入边界条件后，可将（16）式转化为：

向量X包含边界上的未知量。

1.3 系数矩阵的计算

（1）非对角元素的计算。如果源点不位于积分单元内，（13）式和（14）式可采用四点高斯求积公式，即

（2）对角元素的计算。hii的计算，采用均温场的概念，可避免Ci的计算，则

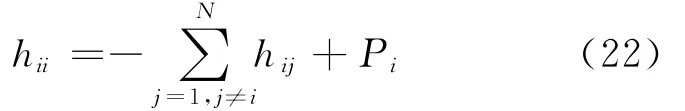
其中

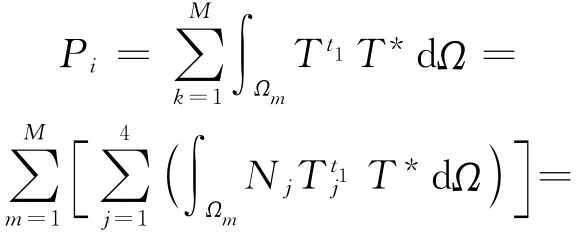
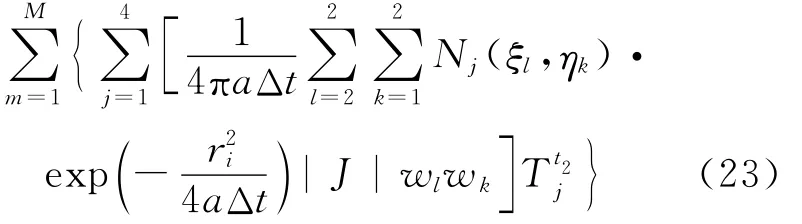
其中，Nj（ξl，ηk）为四点线性插值公式；｜J｜为坐标变换的雅戈比行列式。和的计算如下：

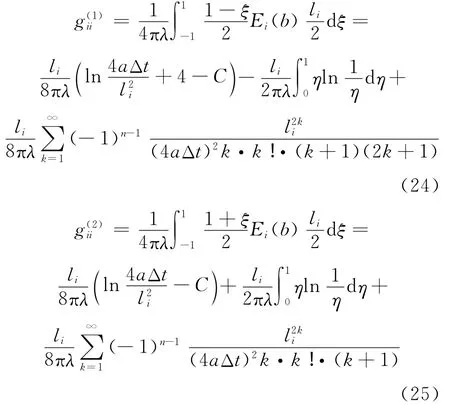
2 反问题

2.1 目标函数

在反问题中，热扩散系数a或导热系数λ是未知的，其他条件与正问题相同。本文反问题中需要的额外条件是热通量。反演的优化目标函数可以写为（26）式：

其中，x为待反演参数向量；L为热通量测点的个数（x）为测点热通量的计算值；（x）为测点热通量的实际值。

2.2 复变量求导法

求导是反演计算的重要组成部分，求导的精度极大地影响反演的求解精度。通常求导采用有限差分法，对于复杂的系统或函数，差分法很难满足计算精度的要求。复变量求导法最早由文献［15］提出，它把偏导数的计算转化为复域函数的计算，是一种使用方便、计算结果精确的函数偏导数数值计算方法。

对于任意一个实函数f（x），将所求导数的变量x施加一个很小的虚步h，并将其展开成泰勒级数形式：

当h取极小值时，通常可以忽略三阶以上的无穷小量，分别比较实部和虚部可得：

使用复变量求导法求导的精度远远大于普通的差分法，当h取10－30时仍然适用，因此，复变量求导法是求解灵敏度的一个有效方法，在复杂函数的数值求导计算中非常有效。

2.3 共轭梯度法

共轭梯度法的基本思路是把共轭性与最速下降法相结合，利用已知点处的梯度构造一组共轭方向，并沿这组方向进行搜索，求出目标函数的极小点。待反演参数x在第n＋1次迭代时的猜测值为：

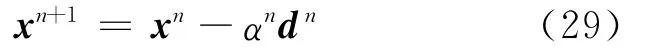
其中，αn为搜索步长；dn为共轭搜索方向，是目标函数的梯度方向与前一次搜索方向的线性组合。dn的计算公式为：

其中，βn为共轭系数，其计算公式为：

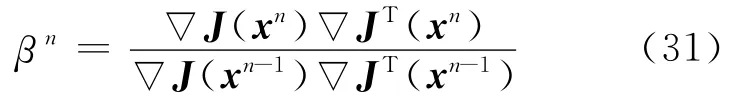
应用复变量求导法的（28）式计算目标函数的梯度：

搜索步长αn可以通过优化目标函数J（xn－αndn）获得：

其中，▽fk为行向量，可由复变量求导法获得。

2.4 反演问题的求解流程

（1）给定某一小正数ε作为收敛精度，选择待反演参数的初始猜想值x0，令n＝0。

（2）求解 （17）式得到测点处的热通量，并判断是否满足‖dn‖＜ε，如果满足则停止迭代，否则继续。

（3）分别按（31）式和（32）式计算共轭系数βn及梯度▽J（xn）。

（4）分别按（30）式及（33）式计算搜索方向dn及搜索步长αn。

（5）令n＝n＋1，按（29）式对待反演参数进行更新，返回步骤（2）。

3 结果与讨论

3.1 算例

考虑一个二维瞬态导热问题，区域Ω是由x＝0，x＝10，y＝0，y＝20构成的一个二维空间。在空间内，x＝0和x＝10的两边是绝热的，空间内的初始温度为0，边界y＝0和y＝20的温度突然变为20。将边界划分为30个线性单元，域内划分为50个四边形单元，如图1所示。热扩散系数和导热系数的精确解a＝5.0，λ＝10.0。在已知测点热通量的条件下，反演a和λ。

图1 单元和节点

3.2 双参数反演

在本节反问题中，材料的热扩散系数a和导热系数λ都是未知的，其他的条件不变。令迭代收敛精度ε为10－4，分别取a和λ的初始参考值为（2，4），选取图1中节点2～5和节点17～20共8个测点，用测点在t＝2s时的热通量反演热扩散系数a和导热系数λ。该算例的热扩散系数a、导热系数λ及目标函数J（x）的收敛曲线，如图2所示，开始时反演计算的收敛速度较快，之后收敛趋于平缓，在经过多次迭代后，导热系数λ和热扩散系数a分别收敛于精确解。本文的方法对热扩散系数a和导热系数λ的同时反演是有效的。

在双参数反演中，选取几组不同的初始参考值，热扩散系数a的反演计算结果如图3所示，导热系数λ的反演计算结果如图4所示。由图可见，选取不同的初始值，最后都能收敛到精确解。

图2 反演参数及目标函数

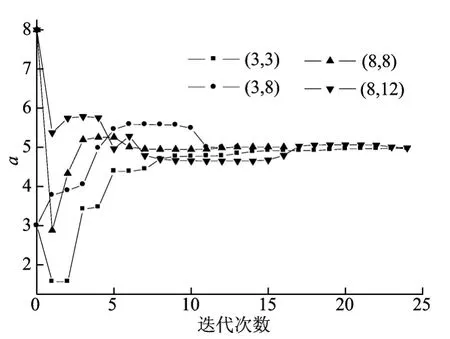
图3 热扩散系数a的计算结果

图4 导热系数λ的计算结果

3.3 随机偏差对双参数反演结果的影响

在双参数反演的过程中，为了研究测量数据的随机偏差对反演结果的影响，选取迭代收敛精度ε为10－4，分别取热扩散系数a和导热系数λ的初始迭代值为（2，4），选取图1中节点2～5和节点17～20共8个测点，分别对测点热通量施加2%和4%的随机偏差，0%是无随机偏差的情况。热扩散系数a和导热系数λ各迭代步的计算结果如图5、图6所示。从图中可见，在施加一定范围的随机偏差后，本文反演方法仍具有很好的收敛性，随机偏差越小，计算结果越趋近于精确解。

图5 随机偏差影响下热扩散系数a的计算结果

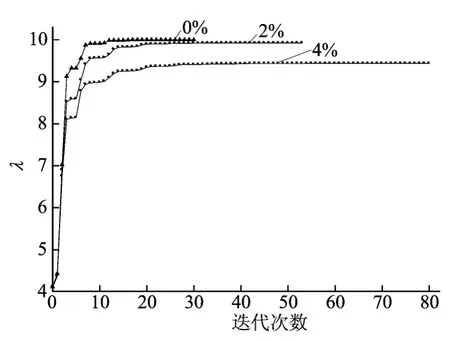
图6 随机偏差影响下导热系数λ的计算结果

没有偏差和施加2%、4%的随机偏差得到的反演结果、其相对误差及终止迭代步见表1所列。热扩散系数a计算结果的相对误差分别0.03%、0.72%、4.48%，导热系数λ计算结果的相对误差分别为0.04%、0.78%、5.68%，迭代终止步数分别为31、54、81。由此可见，施加的随机偏差越大，产生的相对误差也越大，迭代次数也越多。因此，为保证反演的正确性，随机偏差要控制在一定范围内。

表1 随机偏差对反演结果的影响

4 结束语

本文基于边界元法反演了二维瞬态热传导问题的热扩散系数和导热系数。边界元法用于构建二维瞬态热传导问题的数值分析模型，引入复变量求导法求解目标函数的梯度矩阵，共轭梯度法用于优化目标函数获得反演结果。算例表明二维瞬态热传导问题的热扩散系数和导热系数的反演方法有效，具有较高的精度和较好的稳定性。另外选取不同的初始迭代值都能得到精确的反演结果。测量数据的随机偏差越小，计算结果越精确。

［1］ 唐中华，钱国红，钱炜祺.材料热传导系数随温度变化函数的反演方法［J］.计算力学学报，2011，28（3）：377－382.

［2］ 杨海天，薛齐文.两级敏度分析求解非线性稳态多宗量热传导反问题［J］.工程热物理学报，2003，24（3）：463－465.

［3］ 薛齐文，魏 伟，杨海天.多宗量瞬态热传导反演识别［J］.固体力学学报，2009，30（1）：65－69.

［4］ 程荣军，程玉民.带源参数的热传导反问题的无网格方法［J］.物理学报，2007，56（10）：5569－5574.

［5］ Kim S，Kim M C，Kim K Y.Non－iterative estimation of temperature－dependent thermal conductivity without internal measurements ［J］.International Journal of Heat and Mass Transfer，2003，46（10）：1801－1810.

［6］ Yang C Y.A linear inverse model for the temperature－dependent thermal conductivity determination in one－dimensional problems［J］.Applied Mathematical Modelling，1998，22（1／2）：1－9.

［7］ Yang C Y.Estimation of the temperature－dependent thermal conductivity in inverse heat conduction problems［J］.Applied Mathematical Modelling，1999，23（6）：469－478.

［8］ 周焕林，江 伟，胡 豪，等.二维弹性力学边界条件反识别TSVD正则化方法［J］.合肥工业大学学报：自然科学版，2013，36（9）：1076－1081.

［9］ 卞歩喜，周焕林，程长征，等.二维位势边界条件反识别TSVD正则化法［J］.合肥工业大学学报：自然科学版，2014，37（9）：1097－1101.

［10］ Dong C F，Sun F Y，Meng B Q.A method of fundamental solutions for inverse heat conduction problems in all anisotropic medium［J］.Engineering Analysis with Boundary Elements，2007，31（1）：75－82.

［11］ Beck J V.Surface Heat flux determination using an integral method［J］.Nuclear Engineering and Design，1968，7（2）：170－178.

［12］ Huang C H，Yan J Y.An inverse problem in simultaneously measuring temperature－dependent thermal conductivity and heat capacity［J］.International Journal of Heat and Mass Transfer，1995，38（18）：3433－3441.

［13］ Huang C H，Chin S C.A two－dimensional inverse problem in imaging the thermal conductivity of a non－homogeneous medium［J］.International Journal of Heat and Mass Transfer，2000，43（22）：4061－4071.

［14］ Gao X W，He M C.A new inverse analysis approach for multi－region heat conduction BEM using complex－variabledifferentiation method［J］.Engineering Analysis with Boundary Elements，2005，29（8）：788－795.

［15］ Lyness N，Moler C B.Numerical differentiation of analytic functions［J］.SIAM Journal on Numerical Analysis，1967，4（2）：202－210.