一种机械系统非线性类别辨识方法
权双璐,刘杰,韩罗峰,何安琦,李兵
(西安交通大学机械工程学院, 710049, 西安)
一种机械系统非线性类别辨识方法
权双璐,刘杰,韩罗峰,何安琦,李兵
(西安交通大学机械工程学院, 710049, 西安)
针对含刚度非线性连续体系统非线性类别辨识问题,提出了一种基于瞬时频率峰值检测的机械系统非线性类别辨识方法。该方法首先根据被测系统结构特点,分别建立含间隙、立方刚度等5种机械系统常见的刚度非线性系统简化模型;通过研究各模型自由衰减振动瞬时频率分布特点,建立不同非线性模型瞬时频率曲线库;结合图形匹配算法,匹配被测系统实测瞬时频率与曲线库曲线,以匹配结果作为辨识指标,实现非线性类别辨识。将基于瞬时频率检测的非线性类别辨识方法应用于含间隙非线性悬臂梁系统,仿真分析与实验计算表明:被测系统瞬时频率曲线与间隙非线性曲线库匹配较好,匹配值明显小于与其他非线性曲线库匹配结果,验证了该非线性类别辨识方法的有效性。
机械系统;非线性类别;瞬时频率;图形匹配算法
在对非线性机械系统进行动力学分析时,系统特性描述是最重要也是最困难的工作,主要包括非线性作用位置定位和非线性类别描述两大问题[1]。精确的系统特性描述对系统模型的建立及非线性参数的辨识至关重要,一旦系统特性描述不准确将直接导致参数辨识失败[2]。然而,在机械系统非线性类别辨识方面,由于导致非线性振动产生的因素众多,如几何因素,惯性作用、阻尼、边界条件等,使得非线性类别辨识充满挑战[3]。文献[4]通过波特图及奈奎斯特图区分了阻尼非线性与刚度非线性;文献[5]利用伏尔加特级数实现了多项式非线性类别辨识;文献[6]用恢复力曲线图(RFS)直观地区分了机械系统中常见的几种单自由度非线性;文献[2]利用频谱分析辨识了含立方刚度与平方刚度非线性悬臂板系统;文献[7]建立了非线性频域恢复力曲线库,实现了单自由度和多自由度系统非线性类别辨识。虽然上述研究均取得了令人瞩目的成果,但对于机械系统故障分析中常见的含刚度非线性连续体系统,由于不同刚度非线性振动响应间无明显差别,加之连续体系统各单元间运动相互影响,使得其刚度非线性类别辨识更加困难,很少有人在这方面进行研究[4],目前还没有一种方法能有效地解决上述问题[8]。
本文针对含刚度非线性连续体系统,利用被测系统瞬时频率分布特点,提出了一种基于瞬时频率峰值检测的系统非线性类别辨识方法。该方法首先根据被测系统结构特点建立含不同刚度非线性的系统简化模型,仿真求解各模型自由衰减振动响应及其瞬时频率分布曲线;通过研究不同非线性模型瞬时频率分布特点,建立各模型瞬时频率曲线库;结合图形匹配算法,匹配被测系统瞬时频率与曲线库曲线,以匹配结果作为辨识指标,最终实现系统刚度非线性类别辨识。与传统的非线性类别辨识方法相比,本文方法可有效应用于连续体系统非线性类别辨识,并经仿真与实验验证了方法的有效性。
1 刚度非线性系统
在机械系统故障诊断中,由于刚度非线性引起的机械故障频发,常常受到人们关注[9]。本文以刚度非线性系统为主要研究对象,表1列出了几种常见的刚度非线性系统及其恢复力曲线。
根据牛顿第二定律,上述刚度非线性系统自由衰减振动动力学方程为
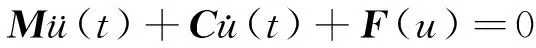
(1)
式中:u(t)为系统响应;M、C分别为系统质量矩阵、阻尼矩阵;F(u)为系统非线性恢复力。
当F(u)=Ku(t)时,系统为线性系统(K为系统刚度),系统固有频率与振动幅值无关
(2)
当F(u)≠Ku(t)时,系统呈非线性振动。系统振动频率不再固定不变,而是由系统基频和一系列高阶谐波叠加而成,随振动幅值变化不断变化。

表1 刚度非线性系统及其恢复力曲线
2 刚度非线性类别辨识
2.1 瞬时频率检测法
根据式(1)及正则化摄动法[10],表1所列的刚度非线性系统自由衰减振动的瞬时频率可估计为系统振动幅值及其非线性刚度参数的函数,即
(3)
式中:a(t)为系统振动幅值;k1,k2,…,kn为系统非线性刚度。
根据式(3)可知,由于刚度非线性函数不同,不同刚度非线性系统自由衰减振动的瞬时频率将呈不同的分布规律,因此可根据瞬时频率分布实现刚度非线性类别辨识。
对非线性时变系统,常用时频分布来估计系统瞬时频率[11]。本文采用时频聚集性能较好且抗干扰强的SPWVD(smoothed pseudo-Winger distri-butions)分布[12],其分布规律为
(4)
式中:h(t)和g(t)为平滑函数且满足h(0)=g(0)=1;u为系统时域响应;ξ为系统频域响应;f(u)为系统响应函数;f*(u)为f(u)的复共轭函数。
其时频
宽度与u(t)相同。记fa(t)=a(t)ejφ(t),则系统瞬时频率为
(5)
式中:a(t)为幅值响应;φ(t)为系统角速度。
本文运用峰值检测法进行系统振动瞬时频率估计,即以每个时间点SPWVD最大值对应的频率作为信号瞬时频率的估计结果。以图1单自由度非线性系统为例,图2给出了表1所列刚度非线性系统瞬时频率分布曲线,系统仿真参数见表2。
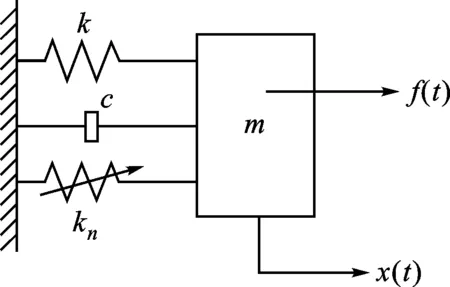
图1 单自由度刚度非线性系统
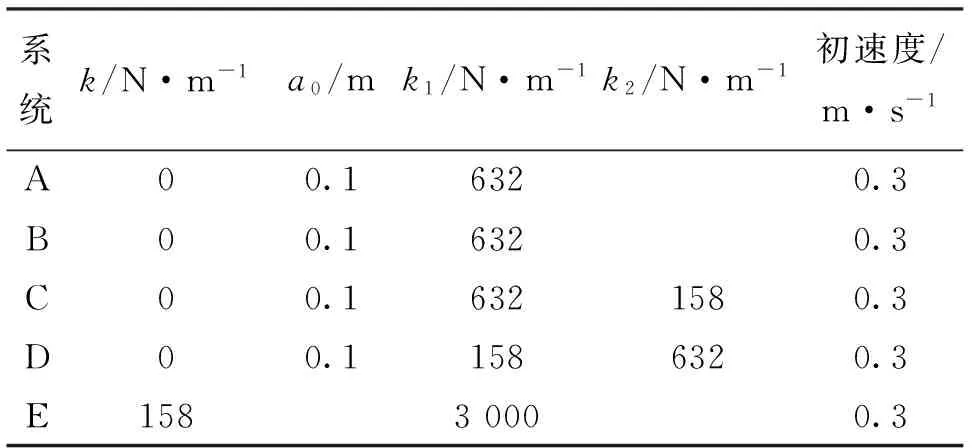
系统k/N·m-1a0/mk1/N·m-1k2/N·m-1初速度/m·s-1A00.16320.3B00.16320.3C00.16321580.3D00.11586320.3E15830000.3
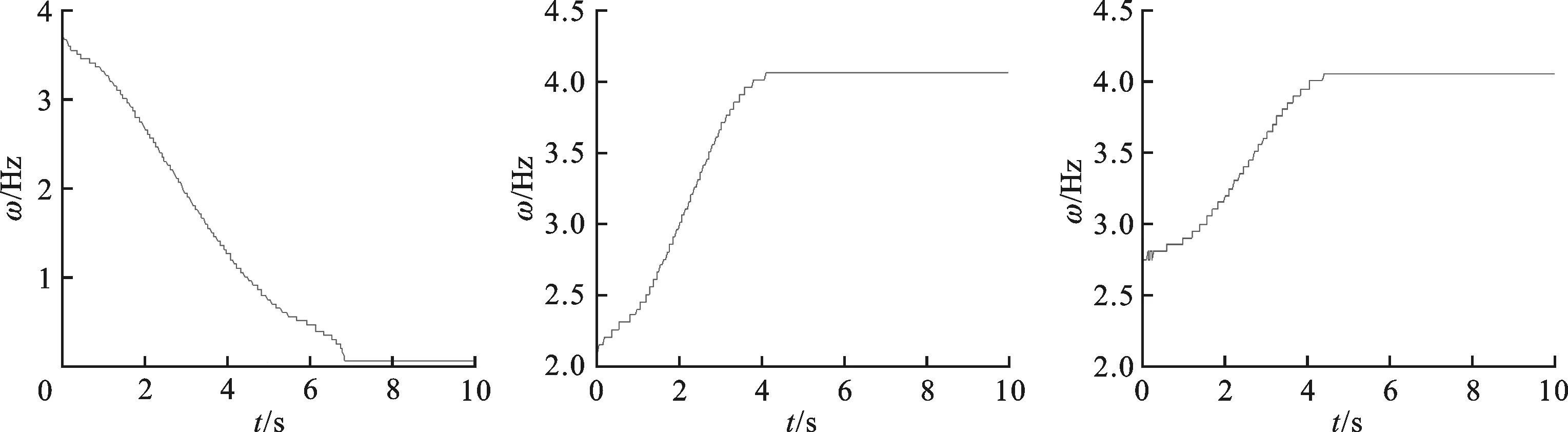
(a)系统A (b)系统B (c)系统C
(d)系统D (e)系统E(硬弹簧) (f)系统E(软弹簧)图2 含刚度弱非线性单自由度系统瞬时频率
从图2中可得,立方刚度系统E瞬时频率分布曲线与摄动法估计的瞬时频率变化趋势相同,即
(6)
为二次曲线,可直接从其他几类非线性系统中区分出来。系统A、D,系统B、C瞬时频率分布曲线相似,这是由于系统A为系统D的一种特殊情况即k1=0,系统B为系统C的一种特殊情况即k2=0。
2.2 非线性类别辨识
为有效地辨识A、B、C、D 4类分段刚度非线性系统,本文结合被测系统瞬时频率分布特征和图形匹配算法实现非线性类别辨识,其技术路线如图3所示。
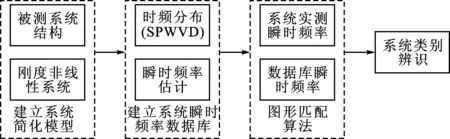
图3 系统非线性分类方法技术路线图
该类别辨识方法基本分为以下3个步骤。
(1)根据被测系统结构特点及刚度非线性系统恢复力曲线,建立含不同刚度非线性的被测系统简化模型,求解相同初始位移下各模型自由衰减振动。
(2)采用SPWVD峰值检测法获得不同模型的瞬时频率变化曲线,建立各非线性模型瞬时频率曲线库。
(3)结合图形匹配算法,匹配被测系统实测自由衰减振动瞬时频率曲线与曲线库曲线,匹配程度最好的系统即为该被测系统主要非线性类别。
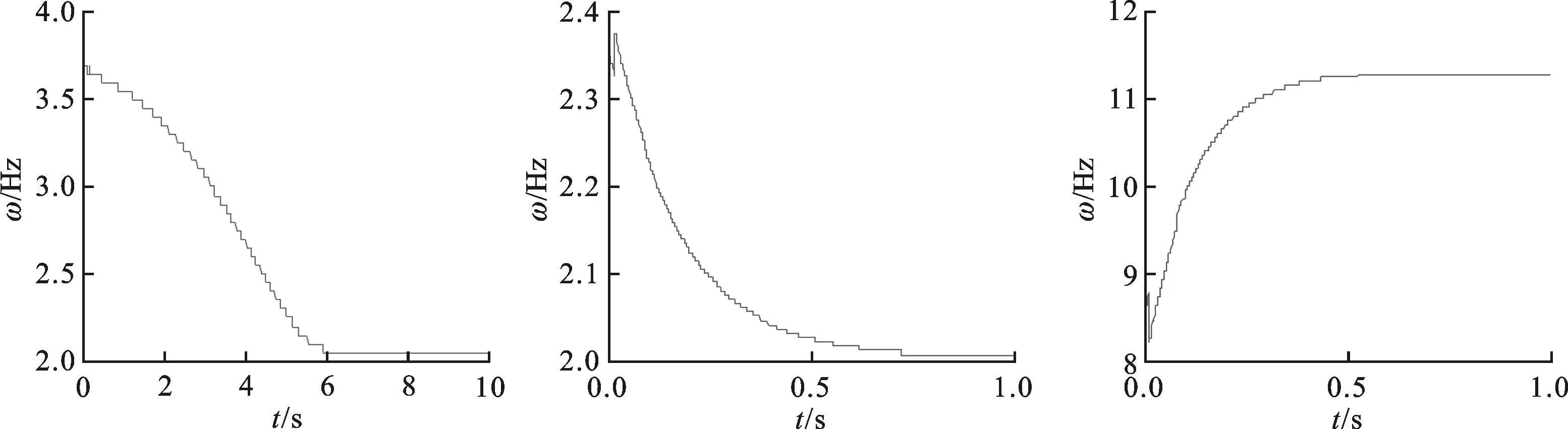
以图1所示的单自由度非线性系统为被测系统,根据系统结构特点,建立含表1所列A~D4种刚度非线性系统简化模型,并求解系统自由衰减振动响应,仿真参数见表3,非线性项参数与表2相同。
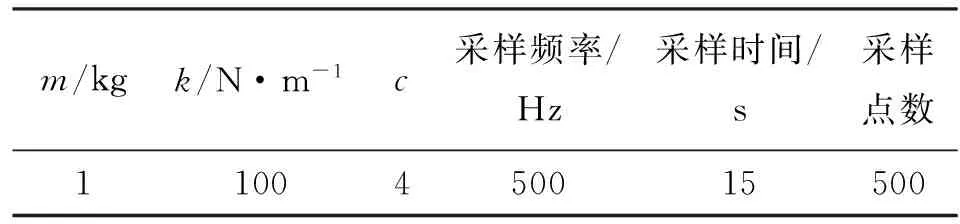
表3 简化模型参数
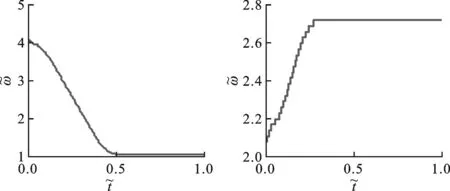
(a)系统A (b)系统B
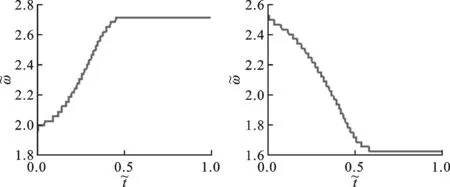
(c)系统C (d)系统D图4 单自由度刚度非线性系统瞬时频率数据库
根据峰值检测法估计各模型自由衰减振动及其瞬时频率分布曲线。为使建立的曲线库具有一定的可比性,瞬时频率分布曲线需进行归一化处理,图4给出了归一化瞬时频率曲线库,纵坐标以系统基频为基准,横坐标以仿真总时长为基准,即
(7)
式中:ω(t)为系统瞬时频率;ω0为系统基频;t为仿真时间;T为仿真总时长。
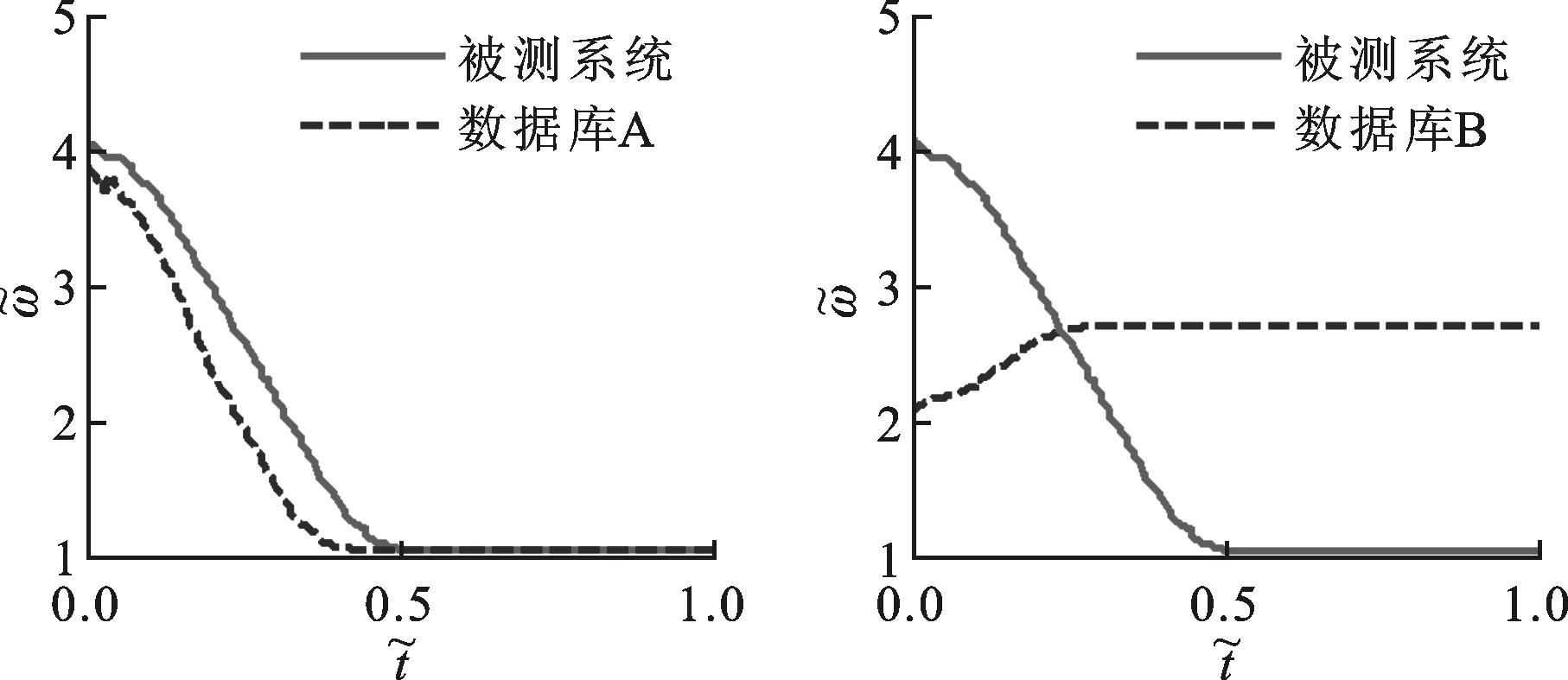
(a)与曲线库A对比 (b)与曲线库B对比
图5给出了被测系统为间隙非线性系统A时,系统实测瞬时频率分布与曲线库曲线对比图。从图中可明显看出,被测系统瞬时频率曲线与曲线库中A类间隙非线性系统瞬时频率曲线接近。考虑结合图形匹配算法,通过匹配被测系统实测瞬时频率与曲线库曲线,实现非线性类别辨识。本文以两曲线间距离作为匹配参数,即
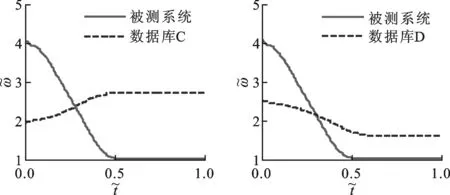
(c)与曲线库C对比 (d)与曲线库D对比图5 被测系统与曲线库瞬时频率对比结果
(8)
式中:YE为被测系统瞬时频率分布曲线纵坐标;YB为曲线数据库内各模型瞬时频率分布曲线纵坐标;N为采样点数。
系统瞬时频率分布曲线与曲线库瞬时频率曲线的匹配结果见表4。从表中可以看出,当被测系统与曲线库对应类别一致时,对应的DS值最小,即两曲线匹配程度最好,从而实现了非线性类别的定量辨识。
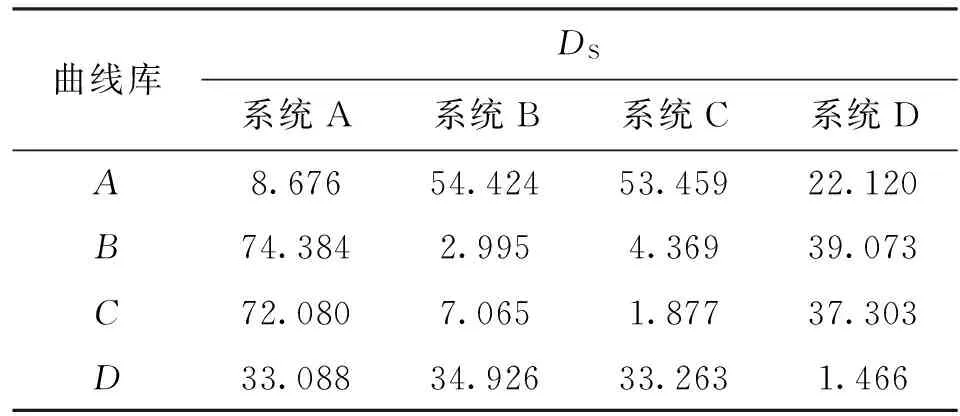
表4 单自由度非线性系统类别辨识DS值
随机选取50组不同间隙与间隙刚度的非线性单自由度系统作为被测系统。图6给出了这50组样本自由衰减振动瞬时频率分布曲线与曲线库匹配结果。从图6中可以明显看出,被测系统瞬时频率分布与曲线库内间隙非线性匹配程度最好,从而确定被测系统为间隙非线性系统。
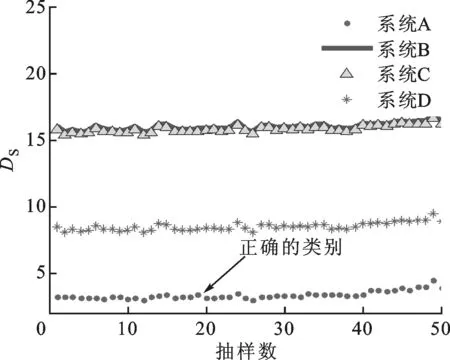
图6 含间隙单自由度非线性系统类别的辨识结果
3 连续体系统非线性类别辨识
3.1 传统方法非线性类别辨识
由于连续体系统各单元间振动的相互耦合,使得传统的非线性类别辨识方法很难实现连续体系统非线性类别的辨识。以图7所示的刚度非线性悬臂梁为例,悬臂梁任意点的位移响应用绝对位移u(x,t)表示,该悬臂梁系统的参数如下:长度l、横截面积A、截面惯性矩I、密度ρ、弹性模量E、非线性位置距离固定端的距离lc、表1所列的刚度非线性项f(u)。
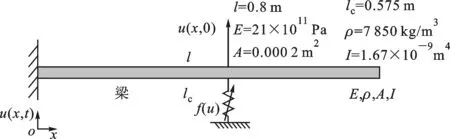
图7 非线性悬臂梁系统
图8给出了立方刚度与间隙非线性系统波特图。从图中可以看出:同一种非线性系统在一定输入输出下,系统幅频响应往往呈现不同的分布。此外,分段非线性系统波特图受非线性影响严重,因此频响函数的形状不能作为确定系统刚度非线性类别的依据[2]。
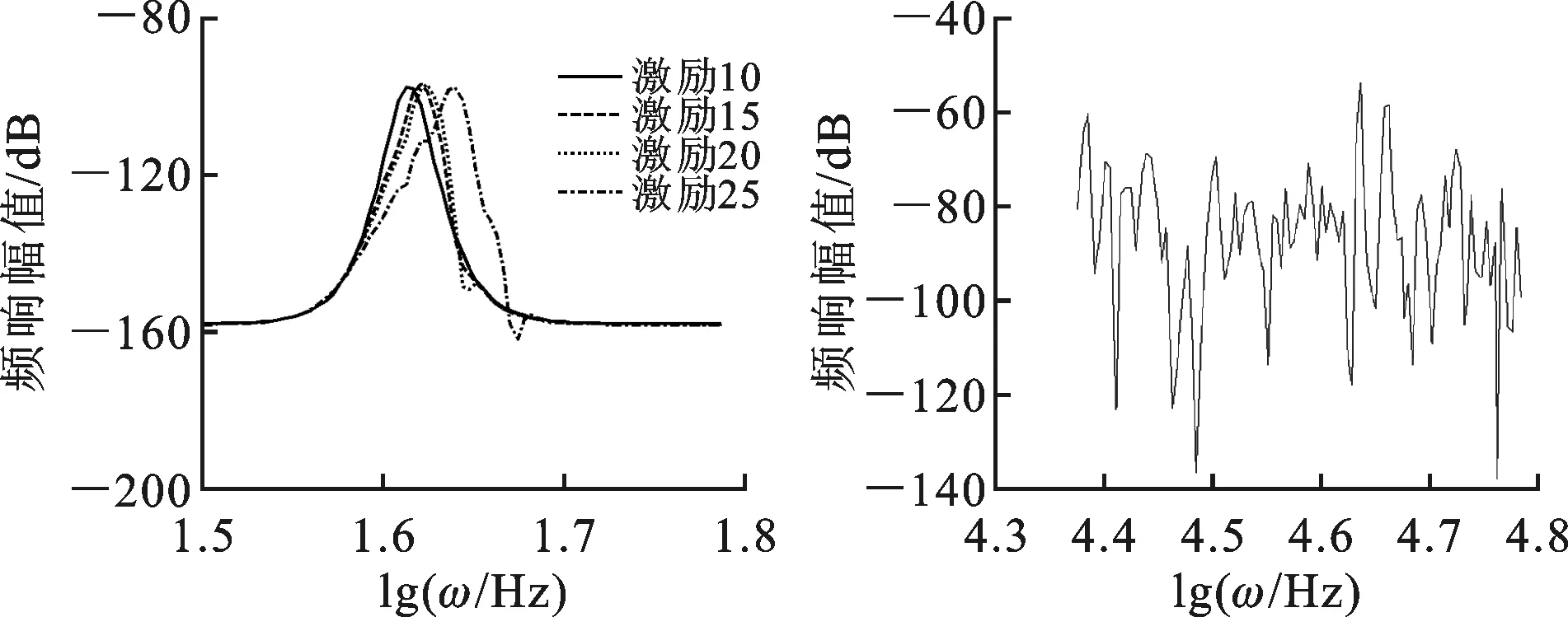
(a)立方刚度非线性系统 (b)含间隙非线性系统图8 刚度非线性系统波特图
图9对比了含间隙单自由度系统及含间隙悬臂梁系统RFS[2]曲线图。从图中可以看出,传统的RFS恢复力曲线法可有效解决单自由度系统非线性类别辨识问题。但是,在连续体系统中,由于系统各单元间会发生进一步相对位移,曲线呈严重的混叠现象,从原始的恢复力-位移曲线分布图中无法准确辨识出非线性类别。
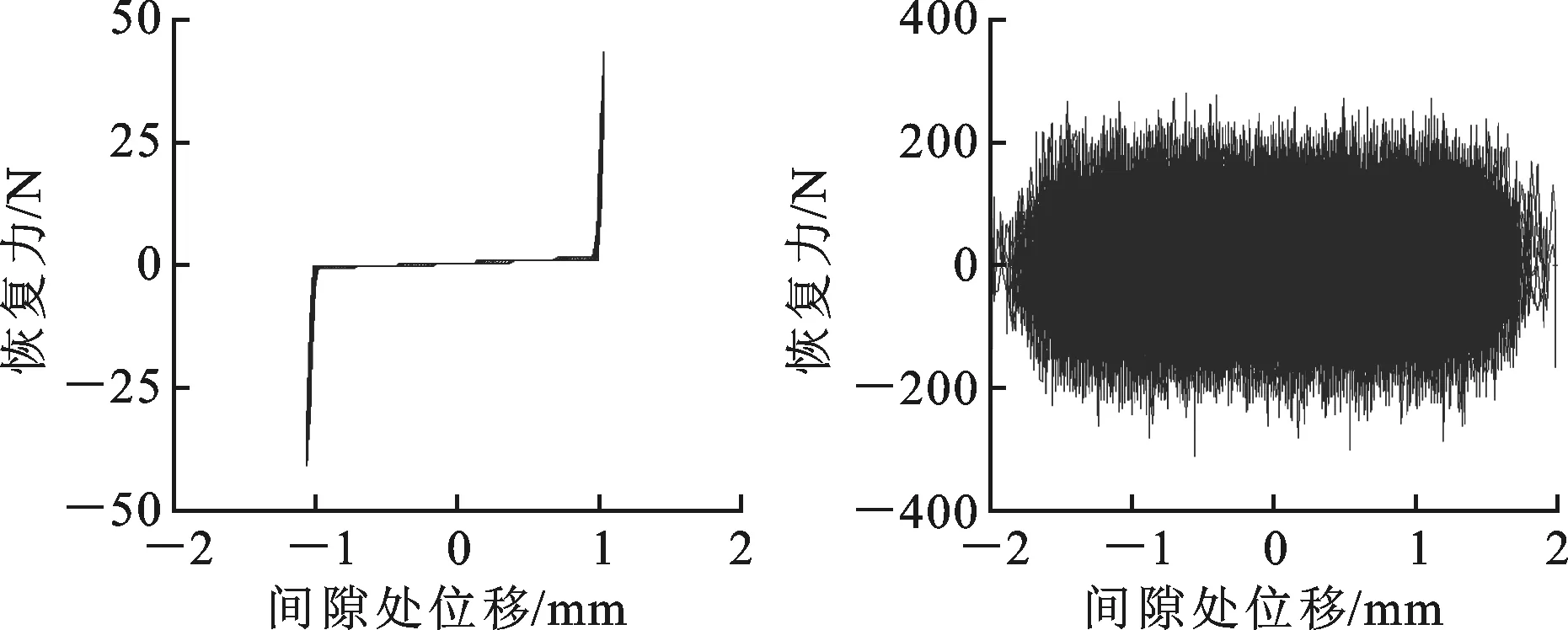
(a) 含间隙非线性单自由度 (b) 含间隙非线性悬臂梁系统RFS图 系统RFS图图9 含间隙非线性系统RFS曲线
3.2 悬臂梁系统非线性类别辨识
根据哈密尔顿原理,图7所示的非线性悬臂梁系统自由衰减振动微分方程为
(9)
式中:utt是u(x,t)关于时间t的二阶导数;uxxxx是u(x,t)关于位置x的四阶导数;fs(x,t)为非线性力。
根据系统边界条件及振形叠加原理,系统固有频率可写为
(10)
其中基频为
(11)
利用本文方法,首先根据系统结构特点及其动力学方程,建立含刚度非线性系统简化模型,并求解模型自由衰减振动响应,仿真参数见表5。
采用峰值检测法获得上述不同刚度非线性系统瞬时频率分布曲线。以基频为基准对各系统瞬时频率分布进行归一化处理,并建立被测系统瞬时频率曲线库,如图10所示。
从图10中可以看出,上述刚度非线性系统瞬时频率均呈不同的分布规律,尤其是立方刚度非线性系统E,其瞬时频率呈光滑二次曲线,可直接从其他几种非线性类别中区分出来。
表5 悬臂梁非线性系统数据库仿真参数

(a)系统A (b)系统B (c)系统C
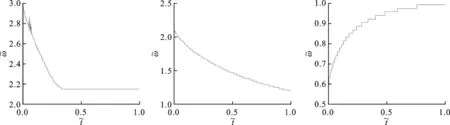
(d)系统D (e)系统E(硬弹簧) (f)系统E(软弹簧)图10 刚度非线性悬臂梁系统瞬时频率分布图
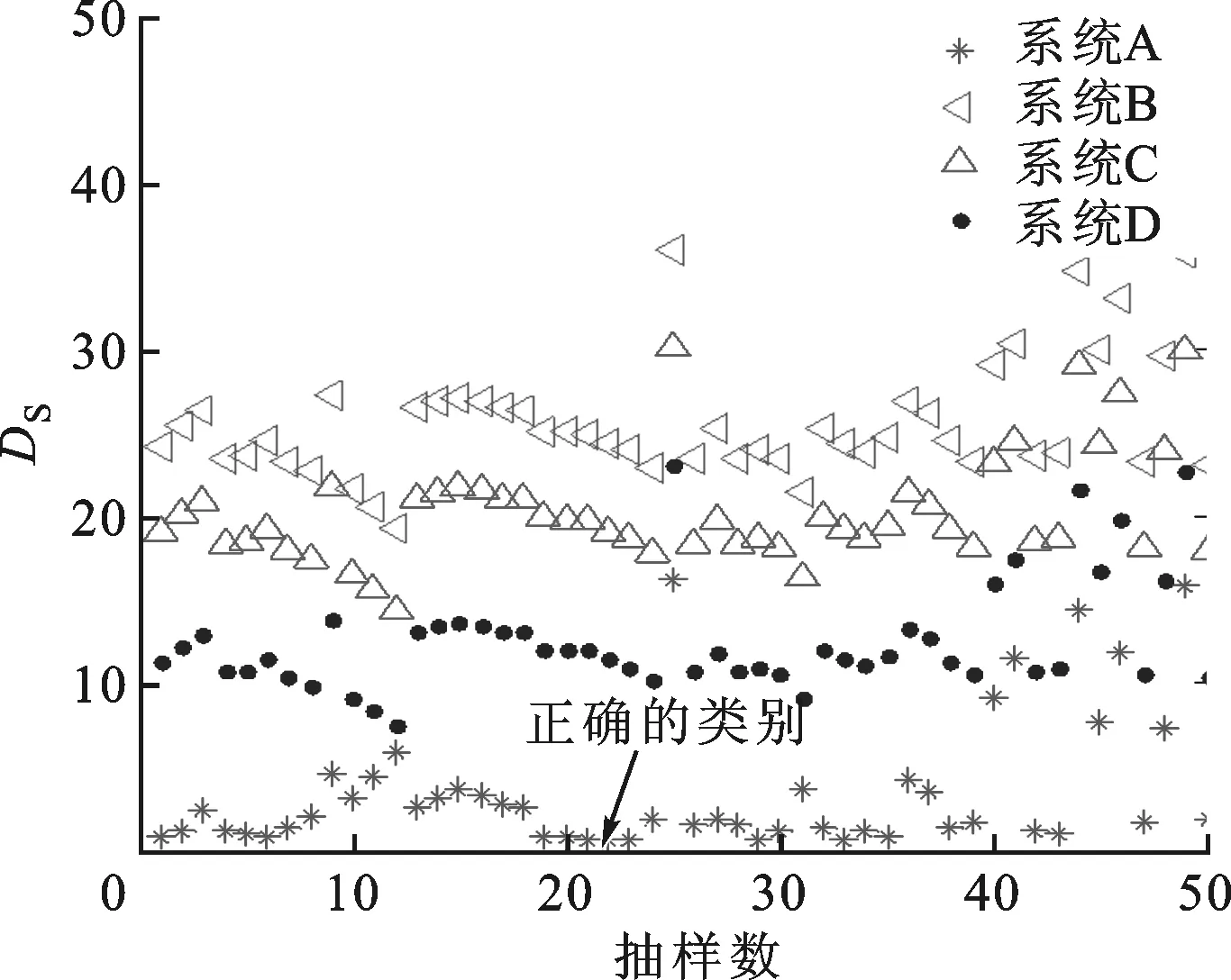
图11 含间隙悬臂梁系统类别辨识结果
以系统A为被测系统,随机选取50组不同的间隙与间隙刚度进行仿真,图11给出了被测系统实测瞬时频率与曲线库图形匹配结果。从图中可以看出,这50组不同间隙非线性系统均与曲线库A的匹配程度最高,从而验证了该类别辨识方法的有效性。
3.3 悬臂梁系统非线性类别辨识实验
本文在假设系统刚度非线性未知的情况下,以系统A为实际被测系统,通过改变系统间隙和间隙刚度验证该类别辨识方法的有效性。实验台如图12所示,间隙位于小悬臂梁与悬臂梁之间,通过小悬臂梁厚度调整间隙刚度,通过间隙头与间隙梁之间的垫片厚度调整间隙大小。本实验用敲击法获得初始位移,并通过电涡流传感器及数据采集仪进行数据采集,具体实验参数见表6。

(a)局部放大图

(b)主视图图12 非线性类别辨识实验台
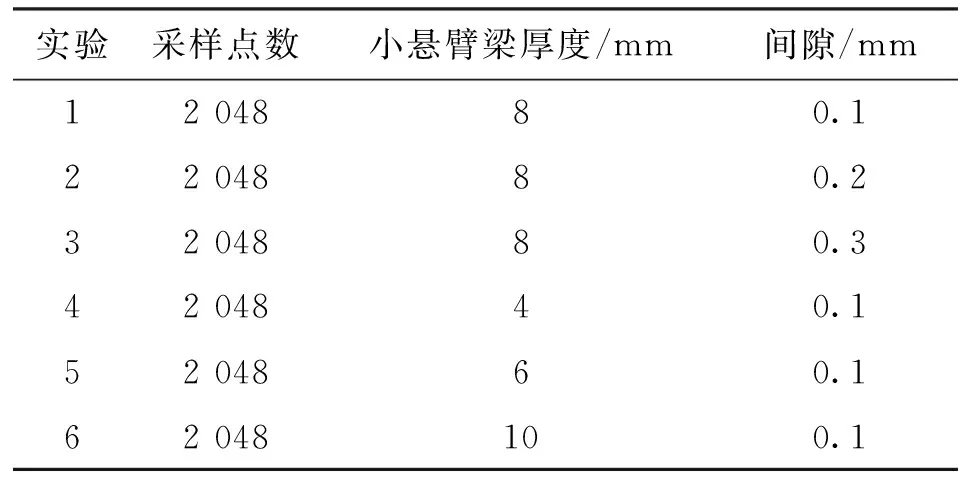
实验采样点数小悬臂梁厚度/mm间隙/mm1204880.12204880.23204880.34204840.15204860.162048100.1
图13给出了间隙为0.1 mm、小悬臂梁厚度为8 mm的衰减响应曲线及其瞬时频率分布曲线,从图中可以看出该被测系统更接近系统A。
分别将上述实验分析结果与悬臂梁非线性曲线库进行瞬时频率图形匹配,匹配结果见表7。从表7中可以看出,被测系统瞬时频率与曲线库A匹配的DS值最小,确定被测系统为间隙非线性系统,从而验证了该方法的有效性。
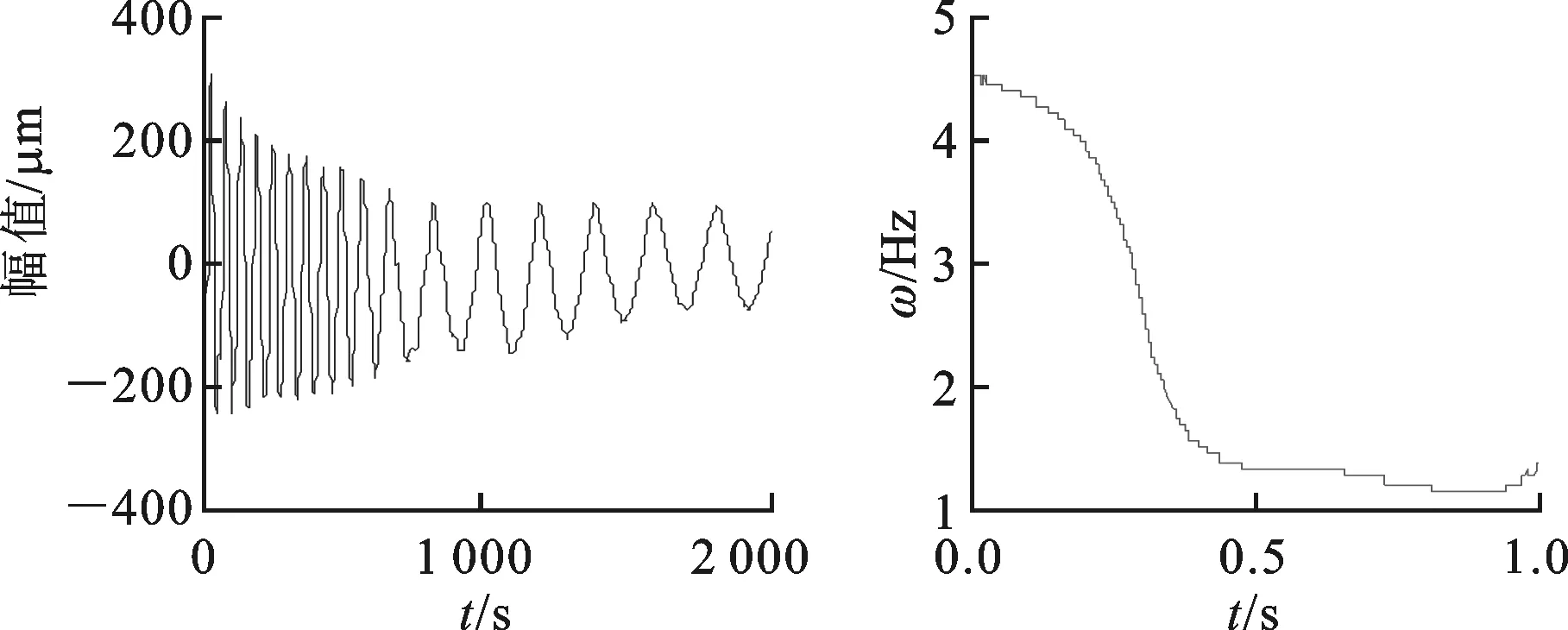
(a)非线性位置自由衰减振动 (b)瞬时频率分布曲线 图13 实验1结果
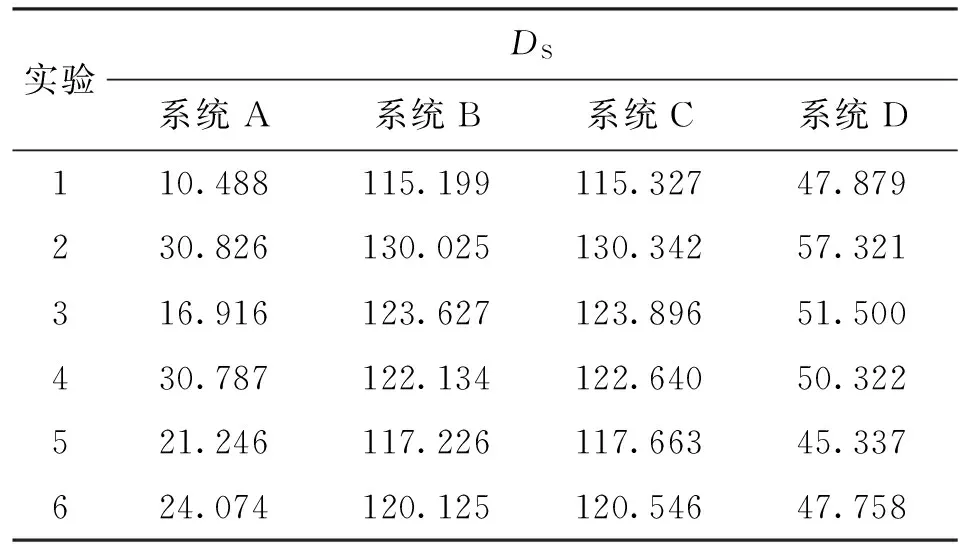
实验DS系统A系统B系统C系统D110.488115.199115.32747.879230.826130.025130.34257.321316.916123.627123.89651.500430.787122.134122.64050.322521.246117.226117.66345.337624.074120.125120.54647.758
4 结 论
本文基于瞬时频率峰值检测,利用被测系统瞬时频率分布特点,提出了一种可用于连续体系统的刚度非线性类别辨识方法。该方法根据被测系统结构特点,建立了含不同刚度非线性系统简化模型及其瞬时频率曲线库,并结合图形匹配算法实现了刚度非线性系统类别辨识。本文通过刚度非线性悬臂梁系统仿真分析与实验计算,验证了该方法的有效性。同时,本文方法对其他非线性具有普适性,可推广应用于机械系统常见非线性的类别辨识中。
[1] ADAMS D E, ALLEMANG R J. Characterization of nonlinear vibrating systems using internal feedback and frequency response modulation [J]. ASME Journal of Vibration and Acoustics, 1999, 121(4): 495-500.
[2] MALATKAR P, NAYFEH A H. A plethora of nonlinear dynamics phenomena observed in a simple cantilever plate [C]∥ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. New York, USA: ASME, 2003: 2603-2610.
[3] GAЁTAN KERSCHEN, WORDEN K, VAKAKIS A F, et al. Past, present and future of nonlinear system identification in structural dynamics [J]. Mechanical Systems & Signal Processing, 2006, 20(3): 505-592.
[4] VAKAKIS A F, EWINS D J. Effects of weak non-linearities on modal analysis [J]. Mechanical Systems & Signal Processing, 1994, 8(2): 175-198.
[5] CHATTERJEE A, VYAS N S. Stiffness non-linearity classification through structured response component analysis using Volterra series [J]. Mechanical Systems & Signal Processing, 2001, 15(2): 323-336.
[6] BENDAT J S, PALO P A, COPPOLINO R N. A general identification technique for nonlinear differential equations of motion [J]. Probabilistic Engineering Mechanics, 1992, 92(7): 43-61.
[7] GONDHALEKAR A C, PETROV E P, IMREGUN M. Parameters identification for nonlinear dynamic systems via genetic algorithm optimization [J]. Journal of Computational & Nonlinear Dynamics, 2009, 4(4): 1724-1732.
[8] BALESTRINO A, CAITI A, CRISOSTOMI E. A classification of nonlinear systems: an entropy based approach [EB/OL].[2014-09-10]. http: ∥www. nt.ntnu.no/users/skoge/prost/proceedings/icheap8-pres07/icheap8webpapers/193%20Balestrino.pdf.
[9] GALLEANI L, PRESTI L L, STEFANO A D. A method for nonlinear system classification in the time-frequency plane [J]. Signal Processing, 1998, 65(1): 147-153.
[10]STROGATS Z, FRIEDMAN M, MALLINCKRODT A J. Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering [M]. New York, USA: Perseus Books Publishing, 1994: 216-227.
[11]COHEN L. Time-frequency analysis [M]. Englewood Cliffs, NJ, USA: Prentice Hall, 1995: 98-153.
[12]张贤达, 保铮. 平稳信号分析与处理 [M]. 北京: 国防工业出版社, 1998: 53-68, 84-92, 392-422.
(编辑 杜秀杰)
Type Identification for Mechanical Nonlinearity
QUAN Shuanglu,LIU Jie,HAN Luofeng,HE Anqi,LI Bing
(School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
For type identification of nonlinear continuum systems with stiffness nonlinearity, a classification strategy with peak detection algorithm is put forward. According to the structure of under test system, simplified models with 5 kinds of stiffness nonlinearity are constructed. The nonlinearity types are particularly interested in structural diagnostic, such as clearance nonlinearity and cubic nonlinearity. An instantaneous frequency library is then set up by studying the free oscillations and instantaneous frequencies of different models. The shape-matching algorithm is used to compare the real instantaneous frequency with the curves in the library. And the results are taken up to the index to identify the nonlinearity types. For a cantilever beam system with clearance, the matching value between the real instantaneous frequency and the curve of clearance nonlinearity measured in this strategy gets obviously smaller than the others, verifying the effectiveness.
mechanical system; type of nonlinear system; instantaneous frequency; shape-matching algorithm
2015-04-17。
权双璐(1991—),女,硕士生;李兵(通信作者),男,教授,博士生导师。
国家自然科学基金资助项目(51475356)。
时间:2015-09-13
10.7652/xjtuxb201512017
TH17
A
0253-987X(2015)12-0104-08
网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150913.1824.006.html

