采用时延估计的外辐射源雷达杂波抑制算法

翟永惠,吴江,王鼎

(解放军信息工程大学信息系统工程学院, 450001, 郑州)



采用时延估计的外辐射源雷达杂波抑制算法

翟永惠,吴江,王鼎

(解放军信息工程大学信息系统工程学院, 450001, 郑州)

针对外辐射源雷达目标探测中监测通道存在分数倍时延杂波而造成杂波抑制性能下降的问题,提出了采用加权子空间拟合时延估计的外辐射源雷达杂波抑制算法(WSF-TDE-CM)。在假设接收数据中的目标信号远远弱于杂波信号的前提下,该算法首先利用接收数据的自相关矩阵通过加权子空间拟合的方法建立杂波时延估计模型,将分数时延估计问题转化为复正弦频率估计的优化问题,然后利用量子粒子群算法求解杂波时延,最后通过估计的杂波时延构造杂波矩阵,将接收信号投影到杂波空间的正交补子空间中,从而实现杂波的抑制。WSF-TDE-CM算法不需要设置滤波器阶数,在杂波时延为分数时延的情况下仍能保持良好的杂波抑制性能。仿真实验表明,当监测通道存在分数倍时延杂波时,WSF-TDE-CM算法与扩展相消算法相比,其杂波抑制比提高了约20 dB;同时,在目标回波信噪比为-30 dB时也能很好地检测到弱目标回波。

外辐射源雷达;杂波抑制;分数时延估计;加权子空间拟合;量子粒子群算法

目前,雷达在军事中的应用越来越广泛。其中,无源雷达将外界的辐射源(如调频广播信号、移动通信信号、电视广播信号和卫星信号等[1])作为发射的信号源,其本身并不向外发射电磁波,因而具有良好的隐蔽性和反侦察性能[2-3]。由于无源探测传播环境的复杂性,监测通道中除了有微弱的目标回波外,还有很强的直达波和多径杂波,在做时频二维互相关时,目标回波的尖峰被杂波信号所淹没,所以只有采用合适的杂波抑制方法才能检测到目标回波。

对于直达波与多径杂波的抑制,目前主要有空域的方法和时域的方法两类。其中,空域的方法[4]主要有自适应波束形成,通常情况下它需要知道目标回波的先验信息,例如目标的来向等。时域的方法主要分为两类:①自适应干扰对消[5-6]的方法,这类方法计算量较小,但对于分数倍时延杂波抑制性能急剧下降,此外这类方法需要设置滤波器的阶数,因此只能抑制时延小于滤波器阶数倍采样周期的杂波;②扩展相消法[7-8](extensive cancellation algorithm,ECA),这类方法没有收敛性的问题,抑制性能较好,但是计算复杂度高,此外与干扰对消法类似,这类方法同样假设杂波的时延在整数倍采样周期处,而这在实际中往往是难以满足的。文献[9]利用矩阵束的方法对直达波与多径杂波的时延与幅度进行估计,然后去除杂波,但是该方法对信噪比的要求较高,在低信噪比的情况下杂波抑制性能急剧下降。

为解决以上问题,本文通过研究信号时延的估计模型与正弦频率估计模型的关系,提出了采用加权子空间拟合和量子粒子群算法进行时延估计的杂波抑制算法。利用子空间拟合算法在低信噪比、小样本情况下估计性能良好的优势来估计杂波的时延,并且通过量子粒子群优化(QPSO)算法解决加权拟合(WSF)中的多维非线性优化问题。仿真实验证明,在低信噪比情况下,该算法的杂波抑制性能和目标检测性能较现有算法有所提升。

1 信号模型

考虑到无源雷达系统的工作环境,杂波可以建模成一小组具有强镜面反射的离散散射中心[7]。这里假设用包含大量这样散射点的反射来模拟一个连续杂波后向散射环境,那么监测通道信号的复包络ssurv(t)可以表示为

(1)

式中:sref(t)是参考通道的信号;D为直达波与多径杂波的总数量;Nj为目标回波的数量;Gmi、Gtj分别为直达波与多径杂波、目标回波的幅度;τmi、τtj分别为直达波与多径杂波、目标回波的时延;ftj为目标回波的多普勒频移;nR(t)是监测通道的热噪声,一般假设为零均值的加性高斯白噪声。

考虑到在进行无源探测时,直达波与多径等杂波的强度远远高于目标回波,即使噪声也比目标回波高数十分贝,因此,针对该模型,可以将式(1)中第2项目标回波与第3项噪声项合并,并对式(1)进行傅里叶变换,可得式(1)的频域表示

(2)

傅里叶变换后,对频域信号采样,设采样的频率为fs,采样点数为N,同时用参考信号对上式进行归一化,可得

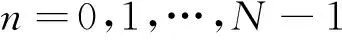
(3)

式中:x(n)=ssurv(n)/sref(n);ne(n)=ns(n)/sref(n)。

令fki=-fsτmi/N,式(3)变为

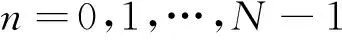
(4)

因此,对监测通道直达波与多径等杂波时延的估计问题转化为了对白噪声中复正弦信号的频率估计问题。

2 基于分数时延估计的杂波抑制算法

2.1 杂波时延估计算法

由于一定情况下,时延估计、正弦频率估计和波达方向(direction of arrival,DOA)估计三者之间具有等效性,可以将DOA估计中的算法应用到时延估计中[10]。在空间谱估计中,子空间拟合这类方法思想简单,性能优越[11]。这里通过加权子空间拟合(weighted subspace fitting,WSF)的方法估计杂波时延,并利用估计的时延抑制直达波与多径杂波。

(5)

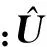
与DOA估计类似,可以得到时延的加权子空间拟合估计[10]为

(6)

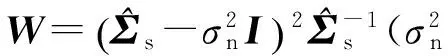
近年来,很多学者采用智能优化算法来求解多维非线性问题。其中较为成熟的是遗传算法,而粒子群算法是一种新兴的基于群体智能的优化方法。这两类方法都有各自的特点,分别可适用于不同的应用场景。其中:遗传算法的健壮性好,但是收敛速度慢,求解精度不够高;粒子群算法收敛速度快,估计精度高,但在求解多峰问题时容易陷入局部最优解。

考虑到外辐射源杂波抑制的应用背景,估计杂波的时延是后续抑制杂波的先决条件,对估计精度和实时性要求较高,因此这里采用量子粒子群算法。此外,针对粒子群算法容易陷入局部最优值的情况,需要设置算法的初始值,以保证最终能够收敛至全局最优解。下面,介绍量子粒子群算法的具体步骤。为保证收敛到全局最优解,首先进行初始值的设置[11]。

(1)初始化。求解仅有τ1时的目标函数值,即

(7)

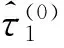
(8)

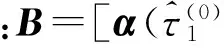
(2)通过QPSO算法进行时延的精确估计。QPSO的粒子更新公式[12]如下

j=1,2,…,D;i=1,2,…,Q

(9)

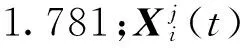
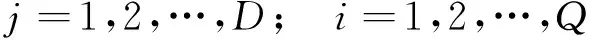
(10)

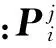
粒子在进化到第t代时在第j维的平均位置用Cj(t)表示,它是所有粒子个体最好位置的平均,其迭代公式为

(11)

式中:β(t)、φ(t)分为[0,1]的随机数。

QPSO算法的目标是找到位置最好的一组解,即寻找适应度函数最大的一组解。这组解即为式(6)所要求解的时延参数。

2.2 采用时延估计的杂波抑制算法步骤

(1)自相关矩阵的构造。对接收数据进行第1节中的处理后,可以得到x(1),x(2),…,x(N),构造如下矩阵

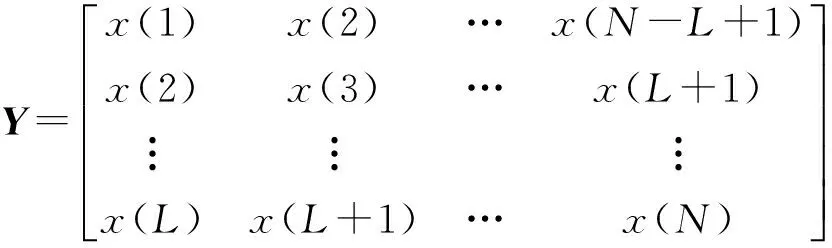
(12)

(2)通过量子粒子群的方法求解式(6)的多维参数估计问题,得到D个直达波与多径的估计时延参数τ=[τ1,τ2,…,τD]。

(3)根据集合τ中的任意一点,可以得到经过时延后的参考信号向量

(13)

因此,由集合中所有点构成的参考向量集合可以组成如下的杂波矩阵

(14)

若使得杂波抑制后信号功率最小化,则直达波与多径杂波抑制可以转化为求解如下的优化问题

(15)

式中,θ为杂波矩阵的加权系数,由最小二乘原理可以得到

(16)

因此杂波抑制后的监测通道信号可以表示为

(17)

式中,P0为投影矩阵,它将接收向量ssurv投影到杂波子空间的正交补子空间上,从而得到目标回波。

2.3 时延估计精度分析

对于参数估计的问题,克拉美罗界(Cramer-Rao bound,CRB)给出了一个最小方程无偏估计器能够达到的最好估计性能。这里可以通过CRB对提出算法的时延估计精度进行评估。文献[13]对于单条与两条多径的情况给出了具体表达式。若假设参考通道sref(k)与监测通道ssurv(k)的信号满足如下模型

(18)

式中:d(k)为直达波;τ1和τ2为两条多径的相对于直达波的时延;λ11、λ21和λ22为相应的幅度增益;w1(k)、w2(k)为高斯白噪声。当τ2=0时,时延估计的克拉美罗下界为

(19)

式中:d(n)的频率范围是(f2,f1);Ps、Pn分别为信号与噪声的功率;Bs、Bn分别为信号与噪声的带宽;Td是信号的持续时间。

3 仿真结果与分析

3.1 时延估计性能分析

为了评估本文WSF-IDE-CM算法的时延估计性能,将本文算法与文献[9]中的矩阵束时延估计(matrix pencil time delay estimation,MP-TDE)和多重信号分类时延估计(multiple signal classification time delay estimation,MUSIC-TDE)方法[14]进行对比。仿真信号采用FM信号,分别在不同目标回波信噪比的情况下做300次独立蒙特卡罗仿真实验。为了方便计算CRB,假设监测通道中只有一条多径,时延为12.927 μs(10.35倍的采样周期);目标回波的时延和多普勒频移分别为375.63 μs(300.5倍的采样周期)和300 Hz。

图1为时延估计的均方根误差与目标回波信噪比的关系图。可以看到,随着信噪比的提高,各算法估计性能均有提升。在低目标回波信噪比的情况下,MP-TDE算法的时延估计精度最低,本文的WSF-TDE-CM算法精度最高,更加接近CRB。这说明本文算法相比其他算法而言能够更加准确的估计出杂波的时延,对于噪声相对不敏感。

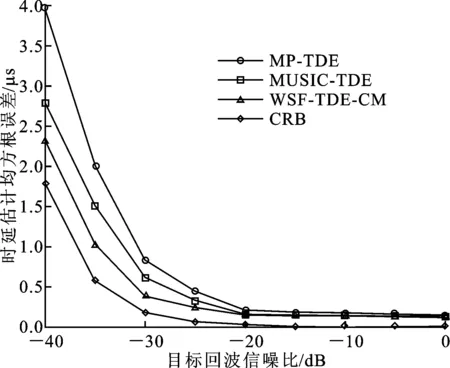
图1 时延估计的均方根误差与目标回波信噪比的关系图

3.2 杂波抑制性能分析

本小节比较了本文算法与文献[6]中的矩阵束时延估计算法的杂波抑制与目标检测性能。设监测通道中的直达波信号的时延与信噪比为[13.281 μs(10.63倍的采样周期),20 dB];有两条多径,其时延与信噪比分别为[125.16 μs(100.13倍的采样周期),13.98 dB]、[250.31 μs(200.25倍的采样周期),13.97 dB];有两个目标回波时,其时延、多普勒频移与信噪比分别为[375.16 μs(300.13倍的采样周期),300 Hz,-30 dB]、[375.94 μs(300.75倍的采样周期),-500 Hz,-28 dB]。

为了验证本文算法在低目标回波信噪比情况下的杂波抑制与目标检测性能,本文将杂波抑制前后监测通道与参考通道信号的互模糊函数图[15]进行对比。图2是在直达波与多径杂波抑制之前信号的互模糊函数图,可以看到,由于强直达波信号的影响,目标回波被淹没在它的旁瓣中,这里只能检测到多普勒频率为0 Hz处的直达波与多径杂波。图3是利用文献[6]方法进行杂波抑制后的互模糊函数图。由于该算法在低信噪比的情况下,时延估计精度急剧下降,不能有效地抑制多普勒频率为0 Hz处的强直达波与多径杂波,只能对其产生大幅衰减,而微弱的目标回波仍然被淹没在多径杂波的旁瓣中,难以检测。图4是利用本文算法进行杂波抑制后的互模糊函数图。可以看到本文算法能够有效地抑制强直达波与多径杂波信号,准确地检测到多普勒频率为300 Hz和-500 Hz处的2个目标回波,且目标的尖峰突出。这是因为本文算法在低目标回波信噪比下也能保证一定的时延估计精度,因此改善了低目标回波信噪比时的杂波抑制性能,提高了弱目标的检测性能。

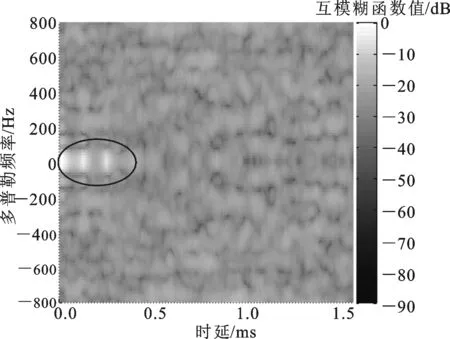
图2 杂波抑制前的信号互模糊函数图

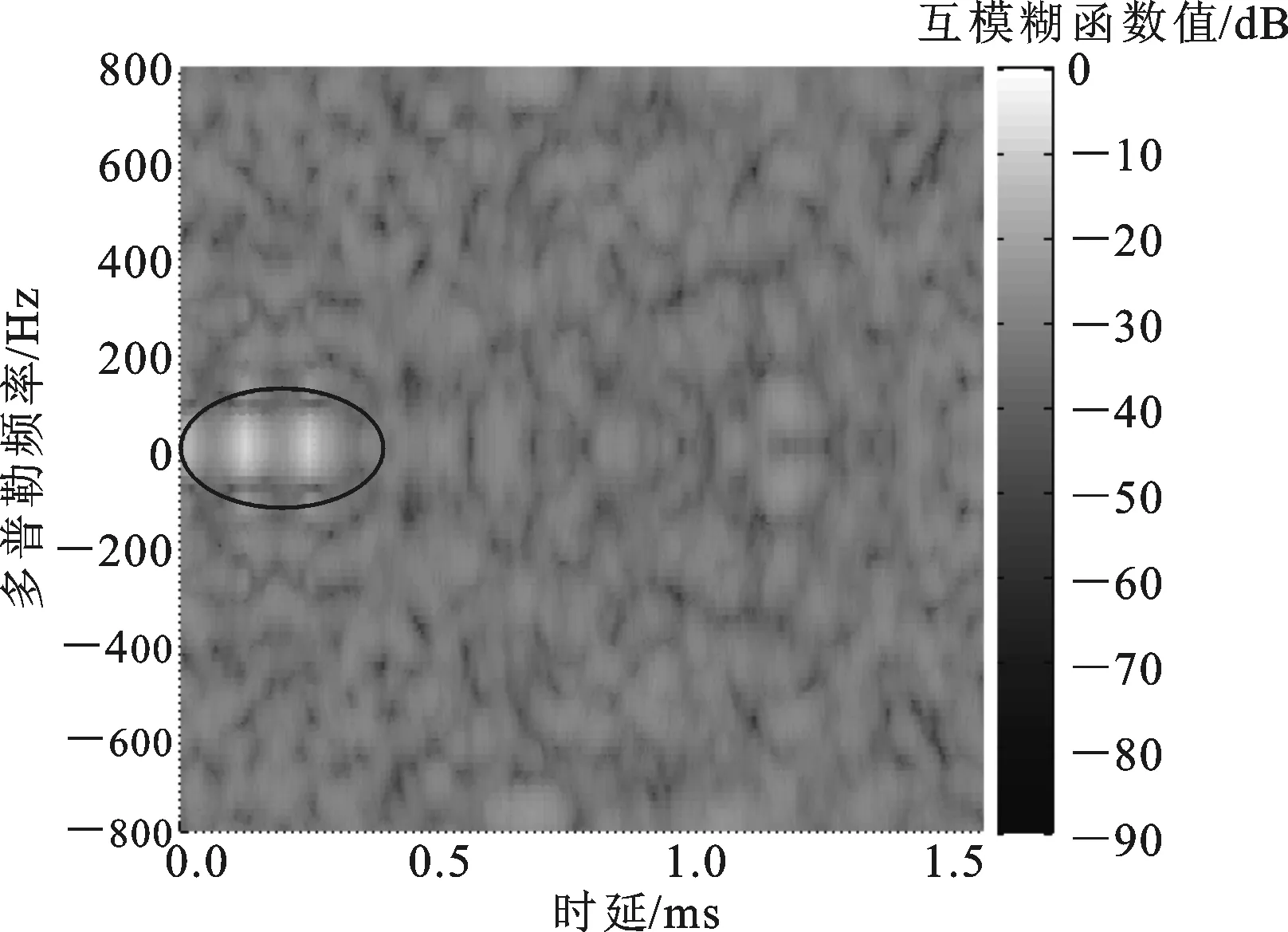
图3 采用文献[6]方法对杂波抑制后的互模糊函数图

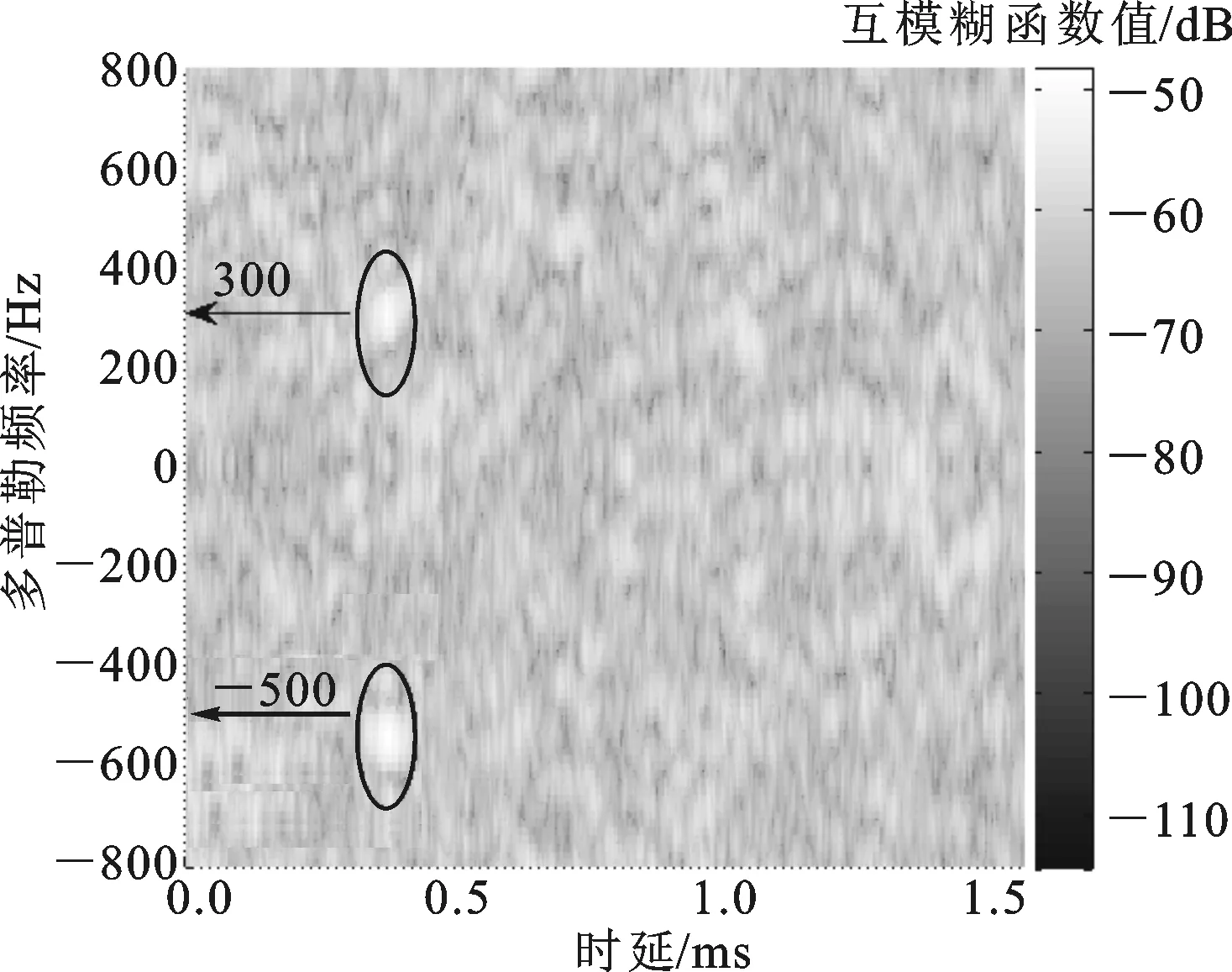
图4 采用本文算法对杂波抑制后的互模糊函数图

3.3 与目前主流算法对比分析

将本文算法与目前直达波与多径杂波抑制的主流算法进行对比,这里仿真了本文算法与归一化最小均方算法(NLMS)、递推最小二乘算法(RLS)和扩展相消算法(ECA)在不同目标回波信噪比情况下的杂波抑制比曲线,仿真参数与3.1节中相同,仿真结果如图5所示。

由图5可见,本文算法的杂波抑制比在目标回波信噪比为-40～0 dB的范围内均高于其他3种算法,尤其在目标回波信噪比增加的情况下,本文算法的优势更加明显。这是因为自适应干扰对消与扩展相消这些方法只能对时延为整数倍采样周期的杂波进行有效抑制,而当杂波的时延为分数倍采样周期时,它们的杂波抑制性能就会急剧下降,本文的WSF-TDE-CM算法能够对分数倍采样周期的时延准确地估计,并有效抑制这些杂波,提高了杂波抑制的性能。

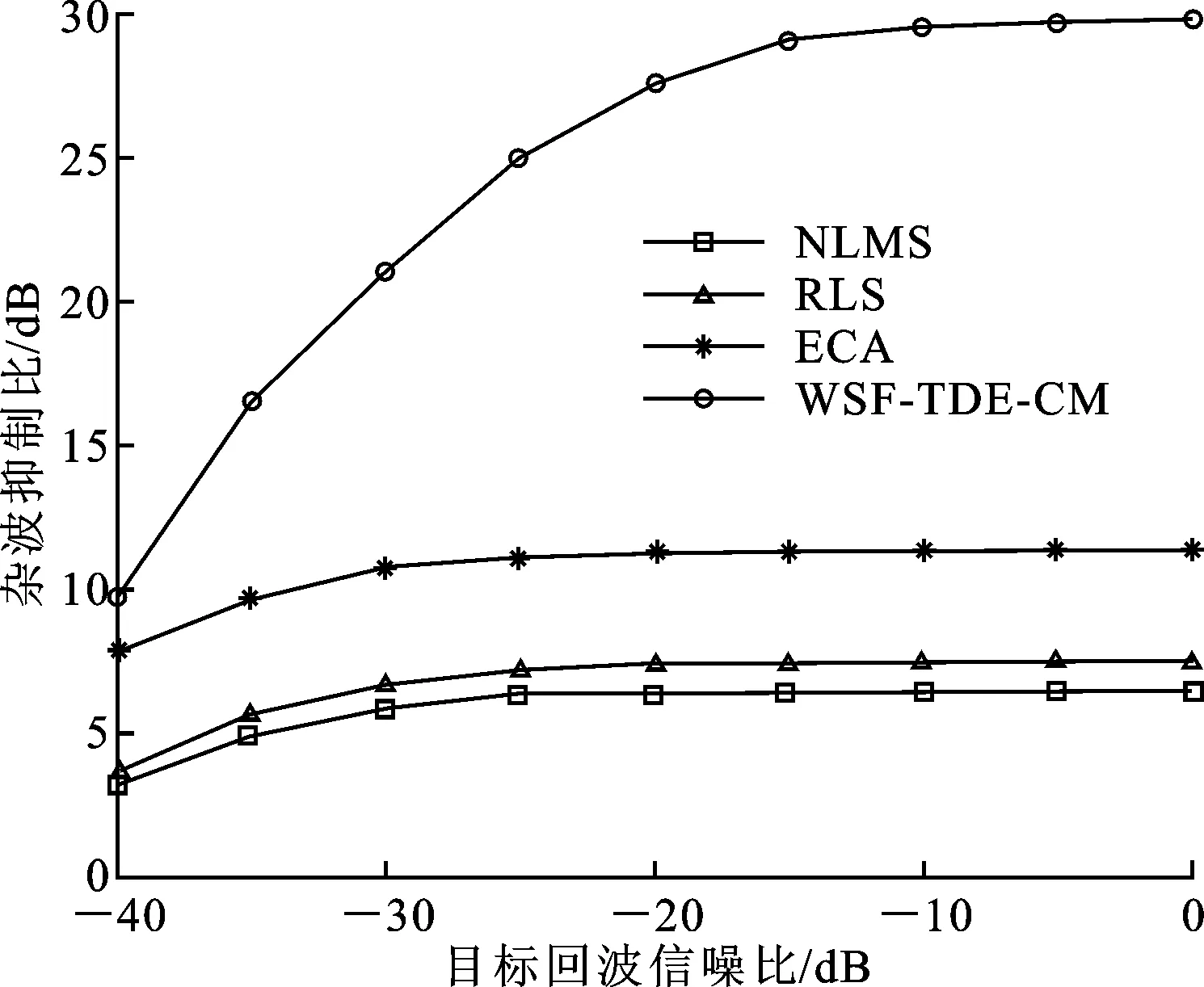
图5 不同算法的杂波抑制性能对比

3.4 计算复杂度分析

本文WSF-TDE-CM算法主要计算量在目标函数的求解以及杂波抑制中,假设有D条待估计的杂波,构造的自相关矩阵的维数为L,数据长度为N。那么,目标函数求解的计算复杂度为O(2D2L+L2D+L3),而杂波抑制的计算复杂度为O(2D2N+N2D+N2),因此总的复杂度为O(2D2N+N2D+N2+2D2L+L2D+L3)。

考虑本文算法属于时域类方法,且图5结果显示ECA算法与本文算法的杂波抑制性能最为接近,因此这里主要与ECA算法进行比较。假设ECA算法抑制M距离单元以内的杂波,数据长度为N,则在构造杂波矩阵时需要(N+M)2M次乘法运算,进行杂波对消时由于矩阵求逆运算需要2M2N+N2M+N2次乘法运算,所以总的计算复杂度为O(4M2N+2N2M+N2+M3)。

由于在接收信号时,天线一般朝向目标信号,主波束之外的杂波得到很大程度的衰减,而主波束内残留的杂波数量一般可以认为是有限的几条,因此相对于N和M,D是很小的;此外,M、L的数量级远小于N,因此数据长度为N在复杂度计算中占主导地位,可以认为本文算法的计算复杂度与ECA算法相当。然而,当远场存在强多径杂波时,ECA算法需要增大M来达到较好的抑制效果,这在很大程度上增加了算法的计算量,而本文算法由于是对杂波的时延进行估计的,因此计算复杂度不会增加。与ECA算法相比,虽然本文算法基本没有降低计算的复杂度,但是在相同复杂度的情况下提高了杂波抑制的性能,这在实际应用中是有一定意义的。

4 结 论

本文提出一种基于加权子空间拟合和量子粒子群时延估计的外辐射源雷达杂波抑制算法——WSF-TDE-CM算法,并与目前杂波抑制的主要算法性能进行了对比。仿真实验表明,在杂波时延为分数倍采样周期时,本文算法的性能远远优于其他算法。此外,本文算法在低目标回波信噪比的情况下仍然有很好的杂波抑制性能,能够较为准确地检测到目标回波。

[1] MALANOWSKI M, KULPA K, KULPA J, et al. Analysis of detection range of FM-based passive radar [J]. IET Radar, Sonar & Navigation, 2014, 8(2): 153-159.

[2] 万显荣. 基于低频段数字广播电视信号的外辐射源雷达发展现状与趋势 [J]. 雷达学报, 2012, 1(2): 109-123. WAN Xianrong. An overview on development of passive radar based on the low frequency band digital broadcasting and TV signals [J]. Journal of Radars, 2012, 1(2): 109-123.

[3] GOGINENI S, RANGASWAMY M, RIGLING B, et al. Ambiguity function analysis for UMTS-based passive multistatic radar [J]. IEEE Transactions on Signal Processing, 2014, 62(11): 2945-2957.

[4] TAO R, WU H Z, SHAN T. Direct-path suppression by spatial filtering in digital television terrestrial broadcasting-based passive radar [J]. IET Radar, Sonar & Navigation, 2010, 4(6): 791-805.

[5] MELLER M, TUJAKA S. Processing of noise radar waveforms using block least mean squares algorithm [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 749-761.

[6] PALMER J E, SEARLE S J. Evaluation of adaptive filter algorithms for clutter cancellation in passive bistatic radar [C]∥Proceedings of IEEE Radar Conference. Piscataway, NJ, USA: IEEE, 2012: 493-498.

[7] COLONE F, O’GAN D W, LOMBARDO P, et al. A

multistage processing algorithm for disturbance removal and target detection in passive bistatic radar [J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 698-722.

[8] 方亮, 万显荣, 易建新, 等. 外辐射源雷达扩展相消批处理杂波抑制算法的调制补偿 [J]. 电子与信息学报, 2014, 36(1): 209-214. FANG Liang, WAN Xianrong, YI Jianxin, et al. Modulation compensation of the batch version of the extensive cancellation algorithm for clutter mitigation in passive radar [J]. Journal of Electronics & Information Technology, 2014, 36(1): 209-214.

[9] LU Hongchao, LI Sichuan, TAN Jin, et al. A new method for direct signal and multipath clutter cancellation in passive radar [C]∥Proceedings of 5th IET International Conference on Wireless, Mobile and Multimedia Networks. Stevenage, UK: IET, 2013: 177-180.

[10]王云龙, 吴瑛. 改进SSMUSIC超分辨多径时延估计算法 [J]. 信号处理, 2014, 30(8): 979-986. WANG Yunlong, WU Ying. Improved SSMUSIC algorithm of super resolution time delay estimation in multipath environments [J]. Journal of Signal Processing, 2014, 30(8): 979-986.

[11]王永良, 陈辉, 彭应宁. 空间谱估计理论与算法 [M]. 北京: 清华大学出版社, 2004.

[12]SUN J, FENG B, XU W. Particle swarm optimization with particles having quantum behavior [C]∥Proceedings of 2004 Congress on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 2004: 325-331.

[13]ZHONG S, XIA W, SONG J, et al. Super-resolution time delay estimation in multipath environments using normalized cross spectrum [C]∥Proceedings of IEEE International Conference on Communications, Circuits and Systems. Piscataway, NJ, USA: IEEE, 2013: 288-291.

[14]GE Fengxiang, SHEN Dongxu, PENG Yingning, et al. Super-resolution time delay estimation in multipath environments [J]. IEEE Transactions on Circuits and Systems: I, 2007, 54(9): 1977-1986.

[15]BERGER C R, DEMISSIE B, HECKENBACH J, et al. Signal processing for passive radar using OFDM waveforms [J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(1): 226-238.

(编辑 刘杨)

A Clutter Suppression Method Utilizing Time Delay Estimation for Passive Radars

ZHAI Yonghui,WU Jiang,WANG Ding

(College of Information Systems Engineering, The PLA Information Engineering University, Zhengzhou 450001, China)

A novel clutter suppression method utilizing weighted subspace fitting time delay estimation (WSF-TDE-CM) is proposed to improve the performance degradation when the clutter has fractional time delay in external illuminators based radar. The method establishes a time delay estimation model by exploiting the weighted subspace fitting algorithm under the assumption that the target echo is far weaker than the clutter in the receiving signal. Then the model is solved by the quantum-behaved particle swarm optimization to obtain the estimated time delay, which is utilized to construct the clutter matrix. Finally, the clutter suppression is implemented by projecting the received signal to the orthogonal subspace of the clutter space. There is no need to set the order of filter in WSF-TDE-CM and the method keeps good cancellation performance even if the clutter has fractional time delay. Simulation results show that compared with the extensive cancellation algorithm, WSF-TDE-CM improves the clutter attenuation by 20 dB when the clutter has fractional time delay, and yields quite good weak target detection performance even when the SNR equals -30 dB.

external illuminators based radar; clutter cancellation; fractional time delay estimation; weighted subspace fitting; quantum-behaved particle swarm optimization

2015-04-12。

翟永惠(1990—),女,硕士生;吴江(通信作者),男,副教授,硕士生导师。

国家自然科学基金资助项目(61201381)。

时间:2015-10-26

10.7652/xjtuxb201512008

TN985

A

0253-987X(2015)12-0047-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151026.2044.004.html