钢桁架人行天桥的振动实测分析与舒适度评价

李 强，单美弟，黄铭枫，陈 驹，冯 鹤

1)浙江大学结构工程研究所，杭州310058； 2)浙江中烟工业有限责任公司，杭州310058



【土木建筑工程 / Architecture and Civil Engineering】

钢桁架人行天桥的振动实测分析与舒适度评价

李 强1,2，单美弟2，黄铭枫1，陈 驹1，冯 鹤1

1)浙江大学结构工程研究所，杭州310058； 2)浙江中烟工业有限责任公司，杭州310058

对连接2栋建筑净跨度达45 m的某曲线型钢桁架人行天桥展开现场人行振动加速度响应实测，得到了在各种行走和跳跃工况下人行天桥加速度响应的现场实测数据.基于希尔伯特-黄变换，对人行天桥结构的动力特性，包括自振频率和结构阻尼，进行了有效识别.利用有限元软件建立了该人行天桥结构有限元模型，分析天桥结构在行人荷载激励条件下的动力响应.对实测数据和数值分析结果进行比对，数值分析结果基本符合现场实测数据.最后，结合国内外规范对该天桥的人行舒适度进行了合理评价.

结构工程；人行天桥；现场实测；人行振动；阻尼识别；有限元分析；振动舒适度

大跨度钢结构人行天桥的自振频率较低，在行人激励下容易引发结构共振.共振会导致结构出现较大的振幅，影响结构的安全和正常使用，也容易导致结构耐久性降低.此外，振动有可能超过人体舒适度耐受极限，给行人心理造成恐慌[1].

在人行桥振动舒适度方面，国内外开展了不少研究[2-4].如陈波等[5]对某斜拉人行桥进行了现场人行振动实测，结合实测数据探讨了现行人行桥振动舒适度评价方法所存在的不足之处.袁旭斌等[6-9]针对人行侧向荷载特性问题进行了研究，通过理论模型阐述了人行桥人致振动机理，建立了人行桥舒适度设计的方法.有限元方法也被广泛地用来模拟人行随机荷载激励，对人行桥进行振动响应分析[10-12].还有学者对现有的舒适度评价标准和人行桥的防振减等课题开展了深入的研究[13-18].

本研究对连接2栋办公楼的曲线型钢桁架人行天桥进行了现场人行振动加速度实测，在实测基础上开展了自振频率和阻尼特性的识别，建立了该人行天桥的有限元模型，完成了天桥人行振动响应的模拟分析，并把数值模拟结果与实测数据进行了比较.最后，结合国际规范对该人行天桥的人行舒适度进行了合理的量化评价.

1 钢桁架天桥人行振动现场实测

图1为曲线型钢桁架人行天桥平面图.该人行天桥总长度约为74.0 m，净跨度约44.5 m.图2给出了天桥的三维示意图.在天桥跨中选择了4个测点，分别为A-1、A-2、A-3和A-4，其中，A-1和A-2布置在天桥的上弦，A-3和A-4布置在天桥的下弦，测点具体位置如图1和图2所示.图3给出了该人行天桥的实景图.采用CA-YD-186型加速度传感器和TST5912动态信号测试仪对该天桥进行了现场人行振动实测.

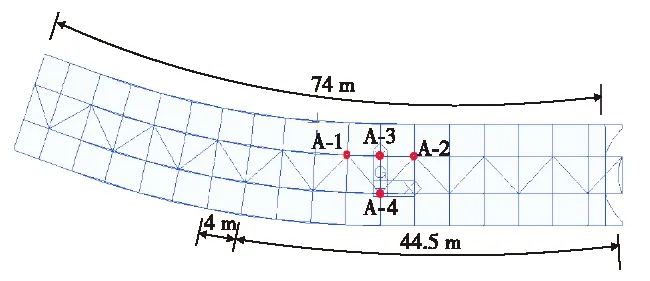
图1 天桥平面图Fig.1 (Color online) Plan view of the footbridge

图2 天桥三维示意图Fig.2 (Color online) 3D view of the footbridge

图3 人行天桥实景图Fig.3 (Color online) Photo of the completed footbridge

1.1 实测工况

1)采用多人同时在人行天桥匀速来回行进作为激励源，每列4人，前后间距1.5 m，测试天桥的竖向加速度等激振响应，分别为工况1(4人齐步走)和工况2(16人齐步走).

2)采用1人起跳或多人同步跳跃作为激励源，跳跃频率约为1.2 Hz，定义如下工况：工况3(1人)、工况4(4人)、工况5(7人)、工况6(8人)、工况7(12人)和工况8(16人). 测试人行天桥在各种跳跃工况下的竖向激振响应.

1.2 实测结果

按照上述8种工况分别完成振动测试，通过结构系统振动特性检测软件，得到每种工况下4个测点位置的加速度响应.图4给出的是工况4(4人起跳)下A-4位置的加速度时程曲线.图5给出了工况7(12人起跳)下A-1位置的加速度数据频谱曲线.表1为8种工况下各测点的最大加速度实测数据.从表1可见，行人齐步走2个工况激励下天桥的加速度响应较小，最大值为0.033 m/s2，甚至小于单人起跳工况激励下的最大加速度0.059 m/s2.而多人起跳的几个工况激励下天桥的加速度响应发生显著变化，最大加速度值随着起跳人数的增加而迅速增大.其中，16人起跳工况激励下测点的最大竖向加速度达到0.155 m/s2.同时，对4个测点位置的最大加速度值进行横向比较，发现测点A-2处得到的加速度值为每种工况下的最大加速度值.A-2 的位置在天桥平面图上位于跨中内凹的部位，而且位于空间桁架的上弦.在后续的模态分析中也发现，这个位置具有较大的模态振型值.

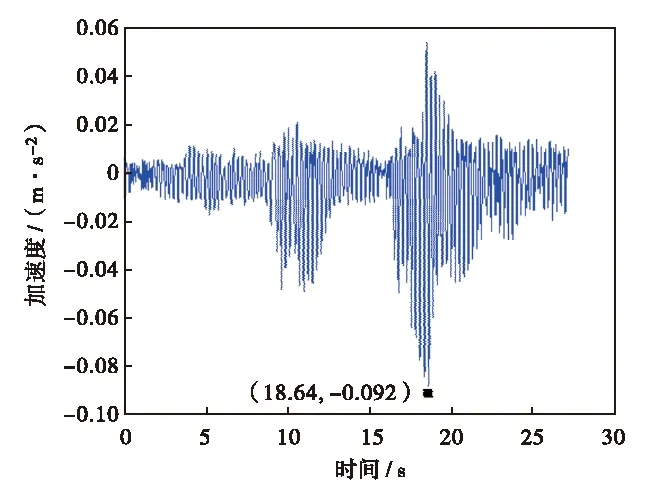
图4 A-4测点加速度时程曲线Fig.4 (Color online) Acceleration versus time at A-4

图5 A-1测点加速度频谱曲线Fig.5 (Color online) Spectrum curve of the measured acceleration at A-1

2 人行天桥动力特性分析与识别

2.1 自振频率的分析与识别

建立了该人行天桥结构的有限元分析模型.主要结构构件采用了桁架单元和梁单元.主要构件的材料和截面尺寸见表2.从图5现场实测的加速度频谱曲线可以看出，天桥在行人荷载的激励下具有较高能量的频率范围，集中在2～8 Hz之间.表3给出了从实测数据识别得到的竖向自振频率，并且与有限元分析得出的结果进行了对比.除了第1阶竖向振型实测的频率比有限元分析结果小14.2%外，其他阶实测自振频率与模型分析结果相比，误差均不超过5%.由此可见，有限元模型基本上能够反映人行天桥实际结构的动力特性.

表1 8种工况下各测点的最大加速度Table 1 Maximum acceleration measured in eight cases 单位：m/s2

表2 主要构件尺寸Table 2 Size of main structural members

《城市人行天桥与人行地道技术规范》[19]规定：为避免共振，减少行人不安全感，天桥上部结构竖向自振频率不应小于3 Hz.但从图5和表3可知，天桥前2阶竖向自振频率均小于3 Hz.具有较低固有频率的天桥结构在行人等外界环境激励下容易发生大幅振动，影响行走舒适度，需要采用国际上相关人行振动舒适度标准进行评价.该人行天桥的人行舒适度评价参见后文.

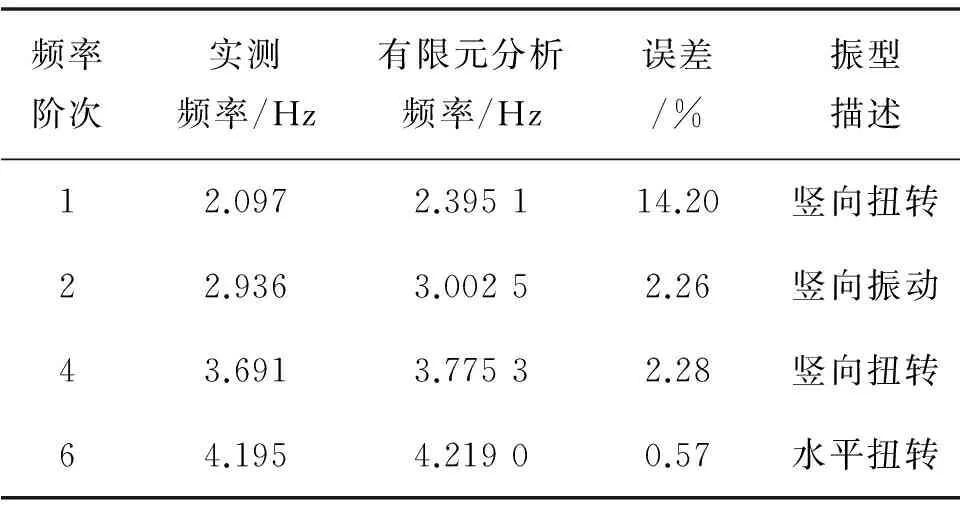
表3 实测与有限元分析得到的固有频率对比Table 3 Comparison of natural frequencies between field measurement and finite element analysis

2.2 结构阻尼的识别

采用希尔伯特-黄变换(Hilbert-Huang transform, HHT)对该天桥结构进行阻尼识别. HHT方法采用经验模态分解(empirical mode decomposition, EMD)，将非线性和非平稳信号分解为多个固有模式函数(intrinsic mode function,IMF)之和，且固有模式函数能很好地适应Hilbert变换[20].因此，HHT方法主要是由EMD和Hilbert变换两部分组成，核心是EMD.

图6 IMF分量的自由衰减曲线Fig.6 (Color online) Free decay curve of the IMF component

图6为IMF分量的自由衰减曲线.图7和图8分别给出了IMF分量对应的幅值曲线、相位角曲线及其拟合结果.最后对IMF分量应用Hilbert变换识别系统的阻尼比，得到其第1阶竖向振动阻尼比约为0.014 8.识别得到的阻尼比可以用于有限元模型的人行振动响应分析.本研究在进行有限元模型的人行振动响应分析时采用了瑞利阻尼模型，并假设前2阶阻尼比相等，将实测识别得到的第1阶竖向振动阻尼比作为前2阶的阻尼比.

图7 对应图6的幅值曲线及其拟合结果Fig.7 (Color online) Amplitude curve corresponding to Fig.6 and the fitting curve

图8 对应图6的相位角曲线及其拟合结果Fig.8 (Color online) Phase angle curve corresponding to Fig.6 and the fitting curve

3 人行天桥振动有限元模型分析

本研究利用有限元模型对行走和跳跃工况下的天桥振动情况进行了模拟分析.限于篇幅，仅介绍跳跃工况(4人起跳和12人起跳)下的有限元模拟分析结果，并与实测数据进行了比较.

3.1 起跳荷载模型

按照BRE行人跳跃模型[21]，行人跳跃荷载可以描述为在一段特定时间tp内有很大的接触荷载，紧接着是双脚离地后的一段零荷载，函数形式为

(1)

其中，Kp=Fmax/G， 为冲击系数，Fmax为动荷载峰值，G为跳跃者自重；tp为接触时间；T为跳跃荷载周期.

根据不同的运动方式，每周期的接触时间tp可以在0～T变化.接触系数定义为

(2)

试验测得有规律跳跃产生的竖向荷载的均值总是等于跳跃者的体重，由此可得冲击系数Kp和接触系数α的关系为

(3)

BRE推荐α一般取1/3，式(1)由此可简化为

(4)

其中，f为跳跃频率.

考虑到现场实测跳跃情况，采用BRE行人跳跃模型，计算时设置跳跃频率为1.2Hz.单人跳跃荷载时程曲线如图9.结构动力分析时采用振型叠加法，特征值分析采用lanczos算法，取了前30阶振型，阻尼比参数设置参考了现场实测阻尼识别的结果.

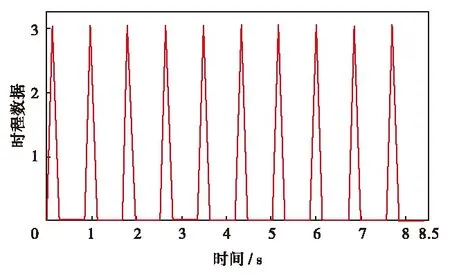
图9 单人跳跃荷载时程图Fig.9 (Color online) Time histogram under jumping load by one person

3.2 起跳工况实测与有限元分析对比

表4和表5分别给出的是4人起跳和12人起跳工况下实测与有限元分析加速度峰值的对比.考虑到现场实测时人群起跳频率不可能完全做到1.2Hz，因此有限元分析得到的加速度峰值会稍大于实测峰值.两表的比较结果也基本符合这一规律.同时对4个测点的加速度峰值响应进行了横向比较，可见与行走工况一样，加速度峰值在测点A-2处取得最大值：4人起跳工况下实测加速度峰值为0.086 4m/s2，有限元分析得到的加速度峰值为0.094 2m/s2，误差为9.00%；12人起跳工况下实测加速度峰值为0.128 0m/s2，有限元分析得到的加速度峰值为0.137 7m/s2，误差为7.6%.

表4 4人起跳实测与有限元加速度峰值对比Table 4 Comparison of peak acceleration between field measurement and finite element analysis under 4-person jump 单位：m/s2

表5 12人起跳实测与有限元加速度峰值对比Table 5 Comparison of peak acceleration between field measurement and finite element analysis under 12-person jump 单位：m/s2

4 人行舒适度评价

选取国际上4个具有代表性的人行舒适度评价标准与规范，对该人行天桥进行了人行振动舒适度评价.具体评价标准与评价结果见表6.

表6中人行天桥的振动指标均是以最不利工况(16人起跳)的实测加速度响应时程为基础数据进行计算的.英国BSI5400规范和欧洲EN1990规范都是以加速度峰值为评价指标的[22-23].从表6可知，该评价指标考虑的因素过于单一，对于人行振动舒适度的控制过于宽松.而国际标准组织ISO2361—1规范和瑞典BRO2004规范则采用加速度均方根作为舒适度指标[24].与瑞典BRO2004规范相比，ISO2361—1规范并没有给出一个简单的指标限值，而是在综合大量有关人体振动的研究工作和文献的基础上，将振动频率由高至低划分为几个范围，给出了相应的振动舒适度曲线，这样的振动指标限值是与频率相关的.实测得到的天桥加速度响应均方值位于曲线下方，因此满足ISO2361—1规范的舒适度要求.

表6 人行振动舒适度评价结果Table 6 Vibration serviceability check

综上4种不同的规范发现，该次人行天桥的现场实测得到的峰值加速度和均方根加速度均满足国际相关规范要求.

结 语

本研究针对某大跨度曲线型钢桁架人行天桥进行了现场人致振动加速度实测分析，在实测基础上进行了结构自振频率的识别，识别结果与有限元模态分析结果较为吻合.同时采用HHT方法识别了人行天桥竖向振动模态的阻尼比.将计算得到的阻尼比应用于人行天桥有限元动力分析模型，进行人行振动响应的分析，得到的加速度响应值与实测结果基本一致，验证了该人行天桥有限元模型的正确性.最后，选取了国际上一些具有代表性的规范对该人行天桥进行舒适度评价验算，结果表明，该曲线型钢桁架天桥结构满足国际相关规范和标准对人行舒适度的验算要求.

/ References：

[1] Cheng Xiongtao. Wind load and wind-induced vibration response analysis of long span footbridge[D]. Shanghai：Tongji University, 2007.(in Chinese) 程雄涛. 大跨度高空天桥风荷载及风振响应研究[D].上海：同济大学, 2007.

[2] He Zongcheng, Wang Baisheng. Vibration test and analysis of long span footbridge[J]. Journal of Vibration and Shock, 2006, 25(4): 138-141.(in Chinese) 何宗成, 王柏生. 大跨度人行天桥的振动影响测试与分析[J]. 振动与冲击, 2006, 25(4): 138-141.

[3] Zhang Guanhua, Ge Yaojun. Vibration characteristics test and analysis of concrete box girder continuous pedestrian bridge[J]. Journal of Vibration and Shock, 2009, 28(2): 102-106.(in Chinese) 张冠华, 葛耀君. 砼连续箱梁人行天桥振动特性测试与分析[J]. 振动与冲击, 2009, 28(2): 102-106.

[4] Feng Peng, Jin Feifei, Ye Lieping, et al. Quantification of pedestrian’s comfort level and dynamic properties of footbridge vibration based on in-situ measurement[J]. Journal of Vibration Engineering, 2013, 26(4): 545-553.(in Chinese) 冯 鹏,金飞飞,叶列平, 等.人行天桥结构振动舒适度定量化与振动特性实测研究[J].振动工程学报, 2013, 26(4): 545-553.

[5] Chen Bo, Wang Xin, Liu Hao, et al. Research on the vibration serviceability of a cable-stayed footbridge based on field measurement[J]. Journal of Wuhan University of Technology, 2013, 35(7): 99-103.(in Chinese) 陈 波, 王 鑫, 刘 浩, 等. 基于实测响应的斜拉人行桥人致振动舒适度研究[J]. 武汉理工大学学报, 2013, 35(7): 99-103.

[6] Yuan Xubin, Sun Liming. Research on pedestrian-induced vibration of footbridge[D]. Shanghai：Tongji University, 2006.(in Chinese) 袁旭斌, 孙利民. 人行桥人致振动特性研究[D]. 上海：同济大学, 2006.

[7] Chen Zhengqing, Liu Guangdong. Pedestrian-induced vibration theory and dynamic design of footbridges[J]. Engineering Mechanics, 2009, A02: 148-159.(in Chinese) 陈政清, 刘光栋. 人行桥的人致振动理论与动力设计[J]. 工程力学, 2009, A02: 148-159.

[8] Sun Limin, Yan Xingfei. Human walking induced footbridge vibration and its serviceability design[J]. Journal of Tongji University Natural Science, 2004, 32(8): 996-999.(in Chinese) 孙利民, 闫兴非. 人行桥人行激励振动及设计方法[J]. 同济大学学报自然科学版, 2004, 32(8): 996-999.

[9] Li Quan. Human-induced stochastic vibration and optimal control for long-span footbridges and floors[D].Beijing：Tsinghua University, 2010.(in Chinese) 李 泉. 人致激励下大跨人行桥及楼盖随机振动及优化 控制[D]. 北京：清华大学, 2010.

[10] Chen Gang, Chen Yuquan, Zhou Jie. Vibration analysis and design on vibration reduction of long-span corridor due to pedestrian excitation[J]. Journal of Yantai University Natural Science and Engineering Edition，2013, 26(2): 151-155.(in Chinese) 陈 刚, 陈玉泉, 周 杰. 大跨度天桥人致振动分析与减振设计[J]. 烟台大学学报自然科学与工程版, 2013, 26(2): 151-155.

[11] Li Dong, Fa Yongsheng, Sun Cuihua, et al. Analysis on pedest rian-induced vibration and comfort evaluation of an footbridge[J]. Building Structure, 2008, 38(6): 50-53.(in Chinese) 李 东, 法永生, 孙翠华, 等. 某人行桥人致振动分析及其舒适度评价[J]. 建筑结构, 2008, 38(6): 50-53.

[12] Yang Lulei, Zhu Xunyan. Analysis on improving walking comfort for large-span corridor structure[J]. Journal of Guilin University of Technology, 2012, 32(3): 425-429.(in Chinese) 杨律磊，朱寻炎．某大跨度混凝土天桥舒适度分析[J]. 桂林理工大学学报, 2012, 32(3): 425-429.

[13] Chen Jieliang. Reasearch on vibration comfort of footbridge induced by pedestrian excitation[D]. Hangzhou：Zhejiang University, 2007.(in Chinese) 陈阶亮. 行人激励下人行天桥的振动舒适性研究[D]. 杭州：浙江大学, 2007.

[14] Fan Jiansheng, Chen Yu, Nie Jianguo. Optimum design of tuned mass damper for footbridge[J]. Engineering Mechanics, 2012, 29(9): 133-140. (in Chinese) 樊健生, 陈 宇, 聂建国. 人行桥的 TMD 减振优化设计研究[J]. 工程力学, 2012, 29(9): 133-140.

[15] Xu Xin. The study of pedestrian suspension bridge’s comfort evaluation and control method[D]. Hangzhou：Zhejiang University, 2010.(in Chinese) 徐 欣. 人行悬索桥舒适度评价及控制方法研究[D]. 杭州：浙江大学, 2010.

[16] Liu Yin. Comfort evaluation for footbridge vibration[D]. Wuhan：Wuhan University of Technology, 2010.(in Chinese) 刘 寅. 人行天桥振动舒适度评价研究[D]. 武汉：武汉理工大学, 2010.

[17] Xiao Xueshuang. Research on human-induced vibration comfort and vibration comfort control for steel pedestrian bridge[D]. Changsha：Changsha University of Science and Technology, 2009.(in Chinese) 肖学双. 钢结构人行桥人致振动舒适度及其控制研究[D]. 长沙：长沙理工大学, 2009.

[18] Jin Feifei. Vibration comfort level design for lightweight FRP footbridges[D]. Beijing：Tsinghua University, 2012.(in Chinese) 金飞飞. 轻质FRP人行桥振动舒适度设计方法研究[D]. 北京：清华大学, 2012.

[19] CJJ69—1995 Technical specification of urban pedestrian overcrossing and underpass[S].(in Chinese) CJJ69—1995城市人行天桥与人行地道技术规范[S].

[20] Chen Jun, Xu Youlin, Li Jie. Hilbert-Huang transform for damping ratio identification of structures with closely spaced modes of vibration[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(4): 34-42.(in Chinese) 陈 隽, 徐幼麟, 李 杰. Hilbert-Huang 变换在密频结构阻尼识别中的应用[J]. 地震工程与工程振动, 2003, 23(4): 34-42.

[21] Ellis B R, Ji T, Littler J D. The response of grandstands to dynamic crowd loads[J]. ICE-Structures and Buildings, 2000, 140(4): 355-365.

[22] BSI5400 Steel, concrete and composite bridges[S].

[23] Gulvanessian H, Calgaro J A, Holicky M. Designer’s guide to EN1990: basis of structural design[M].Glasgow(Scotland): Thomas Telford, 2002.

[24] ISO2631—1 Mechanical vibration serviceability of footbridges under human-induced excitation: a literature review[S].

【中文责编：坪 梓；英文责编：之 聿】

Field measurement-based pedestrian-induced vibration analysis and comfort evaluation of a steel truss footbridge

Li Qiang1,2, Shan Meidi2, Huang Mingfeng1†, Chen Ju1, and Feng He1

1) Institute of Structural Engineering, Zhejiang University, Hangzhou 310058, P.R.China 2) China Tobacco Zhejiang Industrial Co., Ltd, Hangzhou 310058, P.R.China

We carried out a field measurement on the pedestrian-induced vibration of a steel truss footbridge connecting two buildings with a curved planar shape and a net span up to 45 m. Based on the Hilbert-Huang transformation, we effectively identified the dynamic properties of the footbridge, i.e., natural frequencies and damping ratios. We established the finite element mode of the footbridge. The finite element analysis results agree well with those of the field measurements. We also accessed the vibration serviceability of the footbridge using the domestic and international standards currently available.

structural engineering; footbridge; field measurement; pedestrian-induced vibration; damping identification; finite element analysis; vibration serviceability

：Li Qiang，Shan Meidi，Huang Mingfeng，et al．Field measurement-based pedestrian-induced vibration analysis and comfort evaluation of a steel truss footbridge[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(1): 89-95.(in Chinese)

TU 973+.32

A

10.3724/SP.J.1249.2015.01089

国家自然科学基金资助项目(51008275)；交通运输部科技资助项目(2011318223170)

李 强(1991—)，男(汉族)，浙江省奉化市人，浙江大学博士研究生．E-mail：liqiangkimi@zju.edu.cn

Received：2014-07-29；Accepted：2014-11-13

Foundation：National Natural Science Foundation of China (51008275); Ministry of Transport Technology Project (2011318223170)

† Corresponding author：Associate professor Huang Mingfeng．E-mail: mfhuang@zju.edu.cn

引 文：李 强，单美弟，黄铭枫，等．钢桁架人行天桥的振动实测分析与舒适度评价[J]. 深圳大学学报理工版，2015，32(1)：89-95.