散粒体的自组织临界性分析

蒋红英，宋亮亮，罗双华，慕青松

1)西京学院土木工程学院，西安 710123；2)西安理工大学基建处，西安 710048；3)兰州大学土木工程与力学学院，兰州 730000



【土木建筑工程 / Architecture and Civil Engineering】

散粒体的自组织临界性分析

蒋红英1，宋亮亮2，罗双华2，慕青松3

1)西京学院土木工程学院，西安 710123；2)西安理工大学基建处，西安 710048；3)兰州大学土木工程与力学学院，兰州 730000

基于二维模拟实验，研究竖向荷载下散粒体中的自组织临界性，揭示细观拱效应与宏观大崩塌的变化规律，以及拱效应与材料性质的关系.散粒体中每个小自组织的临界发展过程包括自组织搭拱、拱随遇平衡和拱崩塌的动力学演化.散粒体大坍塌是众多小自组织临界发生后的力学性质由量变到质变的过程.用随机理论细观探讨一个预期失败模式的理论模型，为研究散体材料结构自组织临界性系统的可预测性及灾害预测预报提供了科学依据.

防灾减灾工程；防护工程；散粒体；各向异性；自组织临界性；拱效应

散粒体结构中的应力分布具有高度的各向异性[1-2]、搭拱效应引起的卡塞现象[3]和黏滑移动特性[4-5]，工程中有时利用此特性提高承载力，有时则需要避免卡塞.散粒体结构的力学性质从本质上不同于连续介质，其自组织临界性属于非线性动力学问题.从自组织搭拱随遇平衡、以亚稳定状态随遇平衡、自组织逼近临界点，直到崩塌，整个过程均具有复杂和随机的特性.近年来，对散粒体结构性质的研究已有许多成果[6-9]，但仍需要大量的实验积累和理论研究.

散粒体结构的物理性质介于固体和液体之间，它的行为在两者之间转变，有许多不确定性和离散性，没有变形协调的约束，动态性和多变性很强，结构变形是不可恢复的，且在加载和卸载时都会产生．因此散体材料结构中的力学响应分析和工程监控不能以经典的连续介质或岩土力学作为理论指导．目前对散粒体结构的认识、研究及应用于工程问题的分析，还处于初级阶段，未形成方向较为固定、连续性的研究．本文通过试验模拟，针对碎石堆和砾石堆在连续竖向荷载作用下的滑移大崩塌现象，进行了细观的研究，应用随机理论分析散粒体结构的响应，并探讨理论模型，以期为防灾减灾工程及防护工程研究提供参考．

1 试验内容

1.1 试验简述

用直径为5～60 mm的砾石、碎石作为散体颗粒材料, 颗粒的不均匀系数为d60/d10≥10， 其中，d60和d10分别为颗粒材料的限制粒径和有效粒径.砾石是天然粒料，碎石为天然花岗岩碎石，抗压强度为200～300MPa.利用颗粒层剪切移动装置，测量水平位移灵敏度[10-11]，检测2种不同摩擦系数的碎石材料.装入一个内尺寸为20.0cm×50.0cm，壁厚为1.5cm，用普通低碳钢板加工而成的钢盒内，3面刚性侧限，1面边界上连接有6个位移传感器，如图1.由WDW-100万能试验机在盒子顶部中间处通过一个压头缓慢连续地施加荷载，万能试验机连接电脑,每6min记录1次竖向位移、横向位移、相应的荷载及加载时间等数据.进行位移监测的正交试验35次[12]，观测并分析散粒体结构大崩塌过程中自组织临界发生的规律.分别测量一定堆高时竖向沉降量和横向位移量的变化情况，通过压力与位移的关系，进行不同物理性质材料颗粒的对比实验.

图1 试验装置Fig.1 (Color online) Experimental equipment

1.2 试验细观分析

材料颗粒之间相对移动一般为黏滑运动，如图2(a)所示.以fs表示材料之间的最大静摩擦力均值(阈值)，其值取决于颗粒之间的咬合，即力增加而无滑动发生；f0表示最小动摩擦力均值，其值取决于颗粒表面的粗糙度. 黏滑运动是周期性的重复运动，设运动时间为t1， 停止时间为t2， 则黏滑运动的一个周期是t1+t2. 在一个周期内位移距离为x=(fs-f0)/k， 其中，k为加载系统的动态刚度.

图2 砾石、碎石侧限实验中的荷载-位移曲线Fig.2 (Color online) Load-displacement curve from the gravel pile confining compress experiment

试验结果表明，碎石的fs比砾石略高，而碎石的f0比砾石高很多，因此砾石有明显的“振幅”(自组织临界现象)，而碎石相对砾石有更大的摩擦系数，出现了大量的蠕动现象，自组织临界现象并不明显(图2).图2中砾石的黏滑周期弹跳偏差量fs-f0大于碎石，砾石比碎石的波动更加明显，因此砾石比碎石有更大的位移量.这表明粗糙、不规则的颗粒具有更大的剪阻力，所需要的起始动能更大，自组织临界遇到的剪阻力也大很多.对比结果表明，材料各项异性时的应变约束力远大于各项同性时的应变约束力.

由于散粒体材料中存在阻尼力，阻碍了散体材料颗粒的运动, 使其对外界施加的力有一个滞后响应．材料的滞后又导致了内部能量的耗失．散粒体材料中的内部能量耗失——內阻尼，主要发生在颗粒与颗粒之间相互摩擦及咬合处．这种阻尼力与运动速度无关,但与应力有关．颗粒堆中的摩擦阻尼力为

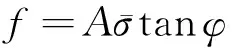
(1)

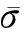
Es=E-Wf=2πr∫τfAdx

(2)

其中，r为颗粒的半径均值．

散粒体中每个小自组织临界的过程包括自组织搭拱、拱随遇平衡和拱崩塌的动力学演化.其中，自组织搭拱和拱随遇平衡是相对慢动力学过程，而拱崩塌是瞬间的快过程[13]，散粒体内部材料颗粒相对移动表现出的是黏滑运动特征[14].“黏”是拱支撑着临界点附近的平衡过程，“滑”由拱的崩塌导致.

材料颗粒移动速度的衰减快慢与颗粒的各向同性或异性有关.若颗粒之间是粗糙表面接触, 颗粒之间的滑动可减少2/3[15]，随遇平衡过程的长短主要与咬合有关.

在竖向荷载作用下, 散粒体结构变形过程可描述为：

1)初始阶段，即应变硬化阶段，散粒体内部逐渐密实，有压密作用，有剪缩现象，是搭散粒拱的过程；

2)峰值阶段，即拱的随遇平衡效应阶段，拱支撑力到达临界值；

3)散粒拱崩塌阶段，即应变软化阶段，局部软化，迅速剪胀，摩擦阻力及咬合作用趋于0，如图3.

图3 散粒体结构变形的3个阶段Fig.3 Three stages of the granular mixtures deformation

2 模型建立

散粒体的自组织临界性是随机的，但也存在规律.在整个散粒体大崩塌过程中，小自组织临界发生的概率满足幂律关系[16-18].散粒体大坍塌源于众多小散粒拱的崩塌，结构的剪切模量逐渐减小，颗粒渐进式地移动，即众多小自组织临界发生后，导致了颗粒相互约束产生的破坏，力学性质也由量变发展到质变.

以S表示散粒体大崩塌的临界状态，对应的加载时间是t，在[0,t]这一加载过程中，S可表示为小自组织临界的叠加：

(3)

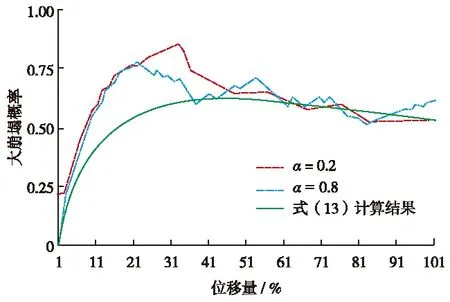
其中，s(t-ti)表示在加载时间ti时，小自组织临界的发生对大崩塌所做的贡献.设t

P(n→n+1， 一个加载时间增量Δt内)=

λ(θ,α)Δt

(4)

其中，λ=E[N(t)]/Δt， 为散粒体中自组织临界发生的强度，E[N(t)]为一次Δt中小自组织临界发生的总量均值， Δt为一次记录的加载时间.λ与结构内的密实度θ和剪阻强度α密切相关，并满足边界条件：在t=0时，有p(0, 0)=1； 对于所有的n≥1， 有p(n, 0)=0. 也就是说没有加载时，没有自组织临界发生的概率为1，而有n次自组织临界发生的概率为0，那么散粒体的破坏过程为Poisson过程[19].试验结果也表明，散粒体整体坍塌过程具有的特征相似于Poisson过程[20-21]，因此式(4)可以表达为

(5)

设内部的变化近似为连续时，式(3)可表示为

(6)

其中，μ(t)=dN(t)/dt，N(t)为自组织临界发生的总量.由于自组织临界过程从自组织搭拱、拱随遇平衡到拱崩塌表现出黏滑特征[22]，因此，该行为可简化为

S(t)=qe-αt，t>0

(7)

其中，q描述颗粒之间的黏强度，即约束颗粒位移的咬合力——拱随遇平衡时间[23]；α为动摩擦系数.

设内部的变化近似连续时，式(3)可表达为

(8)

于是，可以得到随机微分方程

(9)

其中，qμ(t)为随机项，按照Poisson分布的性质，其均值和方差均为λ.

若将随机项定义为一个自组织临界量dN(t)及其均值之差，即

dw(t)=w(t+Δt)-w(t)=

dN(t)-λdt

(10)

则式(9)可变为

dS(t)=[λq-αS(t)]dt+qdw(t)

(11)

其中，将dw(t)可以解释为Wiener过程[20]，即dw(t)=δidt，δi为振幅随机项，属正态分布.

根据随机理论[20-21]得

S(t)=φ(t)[S(0)+∫0tφ(ti)-1λqdti+

qdw(ti)]

(12)

其中，φ(t)=e-αt. 设加载时间t=0时，无自组织临界发生， 即S(0)=0， 所以有

S(t)= e-αt[∫0teαtiλqdti+qδidti]=

t≤ttotal

(13)

其中，ttotal为散粒体大崩塌时所累积的加载时间.式(13)反应了一个大崩塌发生的规律：当小的自组织临界的发生率减少到一定程度时，散粒体大的自组织临界的概率趋于一个常数.这个数主要与材料的咬合随遇平衡效应有关.

3 实例分析

图4 大崩塌概率与位移的关系Fig.4 (Color online) Diagram of the large collapse probability and displacement

4 结 论

本研究基于二维碎石、砾石堆体竖向荷载下大崩塌的试验分析，用随机理论细观探讨了一个预期失败模式的理论模型，定性地揭示了微观拱和宏观大崩塌的演化规律，以及微观拱与材料性质的关系.主要特征有：

1)材料颗粒各项异性时应变约束力远大于各项同性时的应变约束力；

2)散粒体中每个小自组织临界的过程包括自组织搭拱、拱随遇平衡和拱崩塌的动力学演化，散粒体结构大崩塌是由众多小自组织临界发生后内部由量变到质变的过程；

3)具有较低动摩擦的颗粒，波动更加明显，稳定性也更差.

在岩土工程中接触到的散粒材料结构很多,由于散粒材料结构中存在诸多随机因素，因此给散粒体工程的理论研究带来许多困难[24-25].后续将深入进行扩展实验和理论研究，为散体材料结构自组织临界性系统的可预测性以及灾害预测预报提供科学依据.

/ References：

[1] Tasi J C,Voth G A,Gollub J P.Internal granular dynamics, shear-induced crystallization, and compaction steps[J]. Physical Review Letters,2003,91(6):643011-643014.

[2] Jajcevic D, Siegmann E, Radeke C, et al. Large-scale CFD-DEM simulations of fluidized granular systems [J]. Chemical Engineering Science, 2013, 98(5):298-310.

[3] Shirsath S S, Padding J T, Deen N G, et al. Experimental study of monodisperse granular flow through an inclined rotating chute[J]. Powder Technology，2013,246(5): 235-246.

[4] Zheng B, Elsworth D. Strength evolution in heterogeneous granular aggregates during chemo-mechanical compaction[J]. International Journal of Rock Mechanics & Mining Sciences, 2013,60(1):217-226.

[5] Moysey P A, Nadella V R, Malcolm H I B. Dynamic coefficient of friction and granular drag force in dense particle flows: experiments and DEM simulations[J]. Powder Technology, 2013, 93(1):1-14.

[6] Michlmayr G, Cohen D, Dani O. Sources and characteristics of acoustic emissions from mechanically stressed geologic granular media[J]. Earth-Science Reviews, 2012, 112: 97-114.

[7] Samiei K, Peters B. Experimental and numerical investigation into the residence time[J]. Chemical Engineering Science，2013,87(10):234-245.

[8] Ringl C, Urbassek H M. A LAMMPS implementation of granular mechanics: inclusion of adhesive and microscopic friction forces[J]. Computer Physics Communications 2012,183(2): 986-992.

[9] Chen K C, Lan J Y. Micromorphic modeling of granular dynamics[J]. International Journal of Solids and Structures，2009, 46(11): 1554-1563.

[10] Losert W, Geminard J C, Nasuno S, et al. Mechanisms for slow strengthening in granular materials[J]. Physical Review E, 2000，64(2):4065-4068.

[11] Huang J, Silva M V, Krabbenhoft K. Three-dimensional granular contact dynamics with rolling resistance [J].Computers and Geotechnics, 2013,49: 289-298.

[12] Jiang Hongying，Ke Zhihua，Liu Jie. Experimental study of granular materials based on vertical load[J]. Sichuan Building Science，2010,36(3)：106-108.(in Chinese) 蒋红英，柯志华，刘 杰. 竖向荷载作用下散体材料堆的试验研究[J]. 四川建筑科学研究，2010,36(3):106-108.

[13] Sheng L T, Tai Y C, Kuo C Y,et al. A two-phase model for dry density-varying granular flows[J]. Advanced Powder Technology,2013,24:132-142.

[14] Keith A H. Modeling granular material flows: the angle of repose, fluidization and the cliff collapse problem[J]. Planetary and Space Science,2013,82(83):11-26.

[15] Dalibor J, Siegmann E, Radeke C, et al. Large-scale CFD-DEM simulations of fluidized granular systems[J]. Chemical Engineering Science, 2013，98:298-310.

[16] Liu Jiakun. The application of stochastic process[M]. Beijing: Science Press，2000.(in Chinese). 刘嘉馄.应用随机过程[M].北京:科学出版社，2000.

[17] He Na, Fu Ronghua, Bu Xianghang，et al. An experimental study on movement and accumulation characteristics of the sand-sliding slope[J]. Journal of Geological Hazards and Environment Preservation, 2012,23(1):50-53.(in Chinese) 何 娜，傅荣华，卜祥航，等. 散粒体斜坡运动堆积特征试验研究[J]. 地质灾害与环境保护，2012,23(1):50-53.

[18] Jiang Hongying, Lu Jinbu,Mu qingsong. Research on the sedimentation regulation model of the of granular packs[J]. Journal of Kunming University of Science and Technology, 2010(2):78-80.(in Chinese) 蒋红英，鲁进步，慕青松.散体材料结构沉降机理分析与模型建立[J].昆明理工大学学报理工版,2010(2):78-80.

[19] Losert W, Geminard J C, Nasuno S, et al. Mechanisms for slow strengthening in granular materials[J].Physical Review E Volume,2000,61: 4061-4068.

[20] Lin Yuanlie.The application of stochastic process[M].Beijing: Tsinghua University Press，2002.(in Chinese). 林元烈.应用随机过程[M].北京:清华大学出版社，2002.

[21] Zhang Zhuokui, Chen Huichan . Stochastic processes and their applications[M]. Xi’an: Xi’an Electronic and Science University Press, 2012.(in Chinese) 张卓奎，陈慧婵.随机过程及其应用[M].西安:西安电子科技大学出版社，2012.

[22] Huang J, Silva M V, Krabbenhoft K. Three-dimensional granular contact dynamics with rolling resistance [J]. Computers and Geotechnics, 2013,49:49289-49298.

[23] Estrada N, Taboada A .Yield surfaces and plastic potentials of cemented granular materials from discrete element simulations[J]. Computers and Geotechnics，2013,49(11) :62-69.

[24] Guo N, Zhao J.The signature of shear-induced anisotropy in granular media[J].Computers and Geotechnics, 2013,47(8): 1-15.

[25] Nicot F, Hadda N, Guessasma M, et al. On the definition of the stress tensor in granular media [J]. International Journal of Solids and Structures，2013,50(4) ：2508-2517.

【中文责编：坪 梓；英文责编：之 聿】

Analysis of self-organized criticality in the granular mixtures

Jiang Hongying1†, Song Liangliang2, Luo Shuanghua2,and Mu Qingsong3

1) College of Civil Engineering, Xijing University, Xi’an 710123, P.R.China 2) Construction Bureau, Xi’an University of Technology, Xi’an 710048, P.R.China 3) College of Civil Engineer and Mechanics, Lanzhou University, Lanzhou 730000, P.R.China

Based on a two-dimensional experiment, we investigate the mechanism of self-organized criticality of granular mixtures under a vertical load and reveal the rules of change of the mesoscopic arch effect and macro big collapses as well as the relationship between the arch effect and the material properties. The development of self-organization criticality is a geodynamic process including arching, arch relaxation and arch collapse. Large collapse of granular mixtures is a process where quantitative changes lead to changes in mechanical properties after a multitude of small self-organized criticalities occur. We apply random theory to probe into the theoretical model with an expected failure mode, which is given in a mesoscopic discussion. The research on granular structure can provide a scientific basis for the study of the predictability of self-organized criticality system and disaster forecasting.

disaster prevention and reduction engineering; protective engineering; granular mixtures; anisotropy; self-organized criticality; arch effect

：Jiang Hongying, Song Liangliang, Luo Shuanghua, et al． Analysis of self-organized criticality in the granular mixtures[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(1): 96-101.(in Chinese)

TU 444

A

10.3724/SP.J.1249.2015.01096

国家自然科学基金资助项目(10402112)；陕西省科技计划资助项目(2014K06-19)

蒋红英(1959—),女(汉族)，浙江省平湖市人，西京学院教授.E-mail：hunter.000000@163.com

Received：2014-06-17；Accepted：2014-10-11

Foundation：National Natural Science Foundation of China(10402112)； Science and Technology Plan Projects of Shaanxi Province (2014K06-19)

† Corresponding author：Professor Jiang Hongying．E-mail: hunter.000000@163.com

引 文：蒋红英，宋亮亮，罗双华，等．散粒体的自组织临界性分析[J]. 深圳大学学报理工版，2015，32(1)：96-101.