频率不相关性及其在单钥密码系统中的应用

田传俊

深圳大学信息工程学院，深圳 518060



【电子与信息科学 / Electronic and Information Engineering】

频率不相关性及其在单钥密码系统中的应用

田传俊

深圳大学信息工程学院，深圳 518060

探讨频率测度论在保密通信中的应用，研究单钥密码系统中加密变换非线性性质的相关问题．针对目前常见分组密码算法在非线性性质方面缺乏理论规范描述和严格证明的现状，探讨一般单钥密码系统中非线性加密变换严格的数学描述和实现方法．利用频率测度论中的不相关概念，引入不相关单钥密码系统这一新概念，指出这类不相关基本单钥密码系统的存在性，并在理论上严格证明了强大数定律，即在利用不相关基本单钥密码系统进行所有可能的保密通信过程中，当明文单元序列服从离散无记忆均匀分布且密钥周期性更换时，明文序列与密文序列将必然不相关．

数据安全；保密通信系统；不相关单钥密码系统；强大数定律；频率测度论；不相关性

随着数字通信技术的发展，计算机数字通信的安全性日益成为当今的重大科研课题．密码学是一门重要的基础理论，加密技术则是保证信息安全传输和存储的重要技术之一．在最近几十年中，加密算法已引起许多学者的关注，并取得令人瞩目的成就[1-5]．根据现代密码学理论，加密算法可分为单钥密码算法和双钥密码算法，其中，单钥密码算法又可分为分组密码算法和序列密码算法．在现有常见的分组密码算法中，普遍认为加密变换的非线性性质是通过局部的S盒变换来实现的，但迄今为止未见这方面严格的理论证明．

Shannon[1]于1949年创立了基于信息论的保密通信理论，并在密码学理论的发展过程中做出了杰出贡献．他用概率统计的观点对消息源、密钥源、接收和截获消息进行了数学描述和分析，用不确定性和唯一距离度量了密码系统的安全性，阐明了密码系统、完善保密性、纯密码、理论安全性和实际安全性等概念，从而宣告了密码学信息理论时代的到来[2]．

研究分析文献[1-9]发现，基于Shannon理论的现代保密通信理论还存在一些问题．例如，现有保密通信系统的理论安全性概念不明确，相应理论研究所用基础理论知识的综合应用程度不够，导致现有常见密码算法的设计过于注重实际安全性而忽略了理论安全性的基础指导作用；对Shannon提出的完善保密性概念的解释混乱或片面，妨碍了相关问题的深入研究；常见分组密码算法中加密变换的非线性的概念不规范，且利用S盒局部变换的实现方式也缺乏严格理论证明[6-9]．这些问题可能是现有的保密通信系统中相关研究难以深入的主要原因之一．

文献[2-5]指出，目前学者普遍认为保密通信系统既包含完全随机性，又含有伪随机性．因此，综合利用随机性和伪随机性的知识来研究保密系统中的相关问题才更全面或恰当．由文献[1]可知，Shannon建立的保密通信理论在理论安全性的描述或研究中对信息论知识的应用较多，但对伪随机性理论知识在其中的综合应用的论述仍不够深入，因而有必要进一步探讨伪随机性理论在保密通信系统设计中的应用问题．若综合利用随机性和伪随机性理论来研究保密通信系统的设计问题，则有可能获得一些新成果，甚至建立起研究保密通信系统的新方法或密码算法的设计原则．

笔者在文献[10]尝试建立了一门相对独立的基础理论——频率测度论，它是研究序列伪随机性的一门较系统的基础理论，其主要内容与概率论的内容相互对应．可启发人们去探讨频率测度论在概率论的一些应用问题(含现代密码学)中的相关研究．由于频率测度论刚建立不久，还未见有文献讨论它在保密通信中的应用问题．本研究以加密算法非线性性质研究作为频率测度论用于保密通信理论的切入点，给出相关的数学概念和证明方法，尝试综合利用概率论和频率测度论进行保密通信系统理论研究，为今后加密算法设计打下基础．

1 频率测度论的基本知识

本节介绍频率测度论中的一些基本知识[10]．

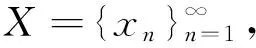
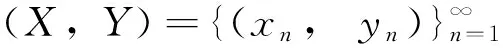
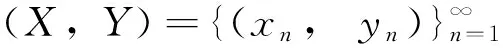
由文献[10]可知，对于任意离散数列(X，Y)， 若E(X)和E(Y)存在，则当且仅当E(XY)存在时， cov(X，Y)存在，且cov(X，Y)=E(XY)-E(X)E(Y)；当且仅当E(XY)=E(X)E(Y)时，X与Y不相关．

2 问题描述

将任一有限集合上一一对应的映射称为置换，本研究着重分析有限整数集合Zn={0，1，…，n-1}上的置换f：Zn↔Zn． 由于不少常见的密码算法都利用了置换作为“置乱”变换，因此，研究置换特性对密码系统的设计具有特殊意义．文献[2]指出，设计分组密码的关键在于找到一种算法，使其能在密钥的控制下，从一个足够大且“好”的置换子集中，便捷地选出置换．然而，如何系统地评估置换的“好”或“坏”仍未有公认的有效方法．本研究将会初步探讨该问题．

Shannon[1]曾将密码(或保密)系统(或算法)定义为从明文空间到密文空间上的一组可逆变换．因此，可将密码系统表示为(M，C，T)． 其中，M为明文空间；C为密文空间；T是从M到C上的一组可逆变换，被称为(理论)密钥变换空间．在保密通信的理论研究中，密码系统(M，C，T)具有重要的基础作用，被称为理论模型．不过，为便于实际应用，密钥变换空间T通常需要利用整数子集K和加密函数E来实现．相应地，所有逆变换T-1要利用K和解密函数D来实现．因此，现代密码学中常用5元组(M，K，C，E，D)表示密码系统．其中，K为(实际)密钥空间；E和D分别是加密和解密变换或函数．为了区别，将(M，K，C，E，D)称为实际模型或综合模型．一般来讲，同一个理论模型可利用多种不同形式的实际模型来实现，因而理论模型是基础．

当前，在实际计算机保密通信的过程中，需选择一个基础的密码系统(M，K，C，E，D)或(M，C，T)进行大量的保密通信．其中，明文和密文空间通常是由所有nbit序列组成的集合(M=C=Z2n)， 这里，n∈N ；M和C中的每个元素通常是加解密函数E和D一次处理的基本单元．此时，将(M，K，C，E，D)或(M，C，T)称为基本密码系统，M、C、T或K中的元素分别称为(基本)单元．根据现代密码学理论和实际保密通信应用的现状，可将保密通信系统的设计分为2个阶段：一是基本密码系统的设计；二是基本密码系统应用过程的设计．在实际应用过程中，保密通信中所有可能的明文是由所有可能的基本明文单元组成的一个随机序列M1，M2，…， 相应的密钥单元序列为K1，K2，…， 密文单元序列为C1，C2，…． 其中，Ci=E(Mi，Ki)，i=1，2，…．

设基本明文与密文空间为M=C=Z2n={0，1，…，2n-1}， 密钥空间为K或T． 当密钥确定后，加密变换Ti：Z2n↔Z2n就是一个置换，被称为(基本)系统置换或算法置换．其中，Ti∈T是利用ki∈K和加密函数E所确定的一个可逆变换，且Ti和ki通常都是相互唯一确定的．这样，基本单钥密码系统的设计通常都等价于一组系统置换的设计．如此一来，一组系统置换的效果就会影响到保密通信的安全性与高效性等．如何评价置换的置乱效果是保密通信系统的基础问题．

保密通信系统的安全性是保密通信的核心．当前，密码系统的安全性分析或评估方法主要有两类：一是由Shannon提出的基于信息论的方法[1]；二是基于现代计算复杂性理论的方法[2]．一般来讲，信息论只能用于描述密码系统内部的各种随机性及其关系，而计算复杂性理论只是用于分析密码系统内部的各种具体变换的计算量。由于一个或多个确定性置换并不包含随机性，且理论上研究这些置换时并未考虑到它们的具体实现方法，因而就不必去分析具体变换的计算量大小. 因此，上述两种评价方法都无法准确地评价一个或多个确定性置换的置乱效果，因而需考虑利用不同的分析方法去评价置换的置乱效果的好坏．由于确定性置换的置乱效果好坏是一种类随机性质，这为利用频率测度论的知识来描述置换的置乱效果提供了可能．

为便于表述，将保密通信中具体的明文、密钥和密文单元分别用m、k(或Ti)和c表示，并将任意随机选取的明文与密钥及其相应的密文单元用M、K(或T)和C表示，则c=E(k，m)或m=D(k，c)， 且C=E(M，K)，或C=T(M)，又或M=D(C，K)． 其中，C=E(M，K)表示当随机变量K和M任意取定一个值时加密函数的取值为C．

若将单钥密码算法或系统的基本明文和密文单元所决定的最大十进制数设为n-1， 则给定一个或所有密钥，可将基本密码算法等效地看成Zn上的一个或所有的系统置换．不妨将所有明文单元排列成自然顺序(0，1，…，n-1)， 并称之为标准数列，当密钥ki或Ti确定后，将所有对应的密文单元设为(c0，c1，…，cn-1)， 则每一个密钥ki或Ti就决定了所有明文单元(0，1，…，n-1)到相应的密文单元(c0，c1，…，cn-1)之间的一个系统置换．其中，i，ci∈Zn和ci=Ek(i)=E(i，k)， 且(c0，c1，…，cn-1)两两互不相同．直观上看，若明文与相应密文单元序列之间是毫不相关或类随机，又或混乱的，则可认为该系统置换的置乱效果较好．因此，当不同密钥决定的系统置换互不相同，甚至不同系统置换之间“毫不相关”时，只要密钥数量足够多，就可认为该基本单钥密码系统在大量的实际保密通信中的应用效果良好．

显然，全体明文单元(0，1，…，n-1)与相应的全体密文单元(c0，c1，…，cn-1)之间的关系是确定的，且它们之间是否“混乱”与保密通信系统的安全性密切相关．若利用频率测度论的知识来描述它们之间“毫不相关”等类似随机的性质，则可利用“频率独立”、“频率不相关”或“频率联合分布”等概念和知识进行描述．本研究仅探讨利用频率不相关的概念来描述单钥密码系统中的系统置换或密钥变换效果好坏的问题．

3 不相关置换

直观上看，用不同的置换将所有明文单元(0，1，…，n-1) “打乱”为密文单元(c0，c1，…，cn-1)的置乱效果是不一样的，甚至不同置换之间的相关程度也不一样．由于密钥空间所决定的每个系统置换是确定的，而密钥和明文的选取是随机的，因此，为全面研究加密变换或系统置换的效果，需综合利用概率论和频率测度论等知识．

由于频率测度论与概率论的主要内容相互对应，因此，参照概率论研究随机性的一些方法可提出研究伪随机性的相应方法．概率论中不相关性和独立性等是研究随机性问题的常用概念，本研究仅考虑频率不相关性在保密通信系统研究中的应用，其他知识应用尚待下一步考虑．

为便于利用频率测度论的知识分析有限个元素所组成的序列间的性质，有必要给出有限序列的相关概念，这有利于设计基本密码系统．

定义7 对于任意2个有限数列L和H， 将L和H进行周期性的无限扩展后所得到的数列X=(L，L，…)和Y=(H，H，…)，分别称为L和H的周期扩展数列．若数列X和Y是频率不相关的，则称相应的有限数列L和H也是(频率)不相关的，由此可类似定义频率独立等概念．

特别地，若任一密钥变换T前后的明文序列M=(0，1，…，n-1)与密文序列C=(c0，c1，…，cn-1)是不相关的，则将该密钥变换T称为不相关置换．由频率测度论(或概率论)可知，不相关置换说明变换前后的两个序列不是线性关系，因此，为保证整个理论密钥空间具有良好性质，可要求基本密码系统中每个系统置换不相关，甚至还可要求任意两个系统置换之间也不相关．

下面用一类具体置换的例子说明不相关置换的存在性与数量问题．

众所周知，幻方可用于构造加密算法中的各种置换，其概念为：对于自然数n>2， 若将数集0，1，…，n2-1(或1，2，…，n2)排列成一个n阶方阵，使得每行、每列和两条对角线上的所有元素之和都相等，则称该方阵为n阶幻方，记为Hn， 并将Hn每行的和n(n2-1)/2称为幻和，并将所有不同的n阶幻方的数目记为ћ(n)[11-13]．

当n>2时，任意n阶幻方都是存在的[11-13]．由文献[13]可知， ћ(3)=8和ћ(4)=7 040． 在说明不相关置换的存在性与应用之前，先将幻方概念稍作推广．

定义8 对任一自然数n>2， 称n阶方阵Gn=(gij)n×n是一个(n阶)广义幻方，如果以下条件成立：

1) (g11，g12，…，g1n，g21，g22，…，g2n，…，gn1，gn2，…，gnn)是(0，1，…，n2-1)或(1，2，…，n2)的一个置换；

本研究将利用广义幻方所构造的置换定义为广义幻方置换．其中，用广义幻方设计M=Zn2上的一个置换作为加密变换T是指T(m)=gij， 这里，m=(i-1)n+(j-1) ∈Zn2．

引理1 设n>2， 且n∈N ，Hn是一个n阶幻方，则将Hn的行或列进行有限次的互换所得到的矩阵Gn就是一个广义幻方．

由引理1可知，n阶广义幻方不仅存在，且所有n阶广义幻方的数量比所有n阶幻方的数量更多．将所有不同的n阶广义幻方的数目称为广义幻方数，记为ρ(n)， 则有ρ(n)≥ћ(n)， 且有ρ(3)>ћ(3)=8和ρ(4)>ћ(4)=7 040．

下面证明广义幻方置换具有不相关性，从而说明不相关置换是存在的，且数量比广义幻方数更多．

定理1 设整数n>2，Gn=(gij)n×n是一个广义幻方，则由Gn按逐行(或列)读取所得到的数列LGn=(g11,g12,…,g1n,g21,g22,…,gn1,gn2…,gnn)与标准数列W=(0，1，…，n2-1)是不相关的．

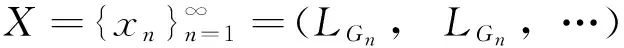
(1)

因式(1)的分子为

0g11+…+(n-1)g1n+ng21+…+(2n-1)g2n+…+(n2-n)gn1+…+(n2-1)gnn=

0(g11+g12+…+g1n)+n(g21+g22+…+g2n)+…+(n2-n)(gn1+gn2+…+gnn)+

(g12+g22+…+gn2)+2(g13+g23+…+gn3)+…+(n-1)(g1n+g2n+…+gnn)=

(2)

因此，covf(X，Y)=Ef(XY)-Ef(X)Ef(Y)=0， 即X和Y不相关．

证毕．

由定理1可知，若将任一n阶广义幻方作为基本密码系统中M=C=Zn2上的一个系统置换，则该置换具有不相关性，因而可以说它是非线性变换，此时可以认为幻方作为加密变换的置乱效果不差．

4 不相关单钥密码算法概念与性质

当前，非线性系统研究已成为众多学者研究的热点，因而有理由要求所设计的保密通信系统的系统置换都是非线性变换．下面将着重讨论一般单钥密码系统具有不相关性的相关问题，利用其理论模型先给出如定义9的“非线性”基本单钥密码系统的概念．

定义9 设基本密码系统(M，C，T)的明文和密文空间为M=C=Zn． 若该基本密钥空间的任一系统置换T满足：基本明文单元序列与利用T对它们依次作加密变换后得到的相应密文序列是不相关的，则将该基本单钥密码系统或算法称为(弱)不相关的，或一般性地称为非线性的．

同时，对于一个不相关基本单钥密码系统，如果该系统中的任意2个不同的系统置换之间也不相关，则将该基本单钥密码系统或算法称为强不相关单钥密码系统，其中，两个系统置换f1：Zn↔Zn和f2：Zn↔Zn的不相关是指由它们所决定的两个序列L1和L2不相关.这里，L1=(f1(0)，f1(1)， …，f1(n-1))；L2=(f2(0)，f2(1)， …，f2(n-1))．

显然，可将不相关基本单钥密码系统的概念推广到任意有限重单钥密码系统(Mr，Cr，Tr)、 甚至所有可能的无限保密通信或无穷维单钥密码系统之中．其中，所有可能的保密通信具有不相关性是指任意的无限明文与相应密文之间必然是不相关的，且Mr=M×M×…×M等. 这对研究实际和所有可能的保密通信是有用的．因此，可以说定义9给出了非线性单钥密码系统的一种严格数学概念．

由定义9和以上讨论，显然定理2成立．

定理2 如果基本单钥密码系统(M，C，T)的基本明文和密文空间为M=C=Zn2，其中，n是一个不小于3的整数，且其基本密钥变换空间T是从ρ(n)个不同的广义幻方中选取的一组广义幻方所确定的置换(如可选│T│=n2或n2的某个正整数倍)，则该基本单钥密码系统就具有不相关性．

备注1 定理2给出了非线性单钥密码系统的一种实现方式，这点与现有分组密码算法中关于加密变换的非线性性质的实现方式略有不同．例如，普遍认为包含数据加密标准(dataencryptionstandard，DES)算法在内的常用分组密码算法中加密变换的非线性性质主要是通过S盒来实现的[6-8]．但S盒只是一种局部的非线性变换，而不相关的系统置换是一种全局的非线性变换，由此可见，如定义9和定理2所定义的单钥密码系统的非线性性质及其相应的实现方式更合理．

备注2 定理2所选取的基本密钥变换空间是否能够利用K=Zn2和某个简单易计算的加密函数E来实现呢？同时，如何从ρ(n)个不同的广义幻方中选取出性能优良的一组广义幻方置换作为理论密钥空间？这些是今后值得研究的问题.

由现有文献可知，将任一基本密码系统用于实际保密通信时，系统的安全性将在很大程度上受到明文和密钥统计特性等实际因素的影响．下面将给出明文单元序列和密钥单元序列满足某种条件时，利用不相关基本单钥密码系统进行所有可能的保密通信也会具有不相关性，因而从非线性角度来看该保密通信具有较为理想的安全性，因为难以利用密文的线性变换对明文做出有把握的统计推断．

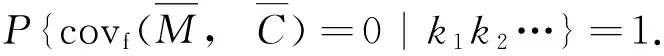
【证】 由已知条件可知，存在正整数q， 使得ki+q=ki， 对任意i=1，2，…，记k1，k2，…=(k1k2…kq)． 由于M1，M2，…是一列相互独立、同均匀分布的随机变量序列，因此，由Borel强大数定律，得

j=0，1，…，n-1

(3)

(4)

其中，Q=(n-1)/2．

(5)

其中，j=0，1，…，n-1；i=1，2，…，q．

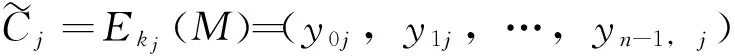
(6)

显然，对任意充分大的整数r>0和u=rq，都有

(7)

其中，rij表示在明文序列M1，M2，…，Mrq中相应利用密钥kj加密所用的明文i出现的次数，对一切i∈Zn和j=1，2，…，q．

由式(5)可得， 对任意i∈Zn和j=1， 2， …，q， 都有

(8)

因此，由式(4)～式(8)和频率互协方差的定义与性质，可得

(9)

于是，定理3的结论成立．

证毕.

类似定理3的证明，还可得到定理4．

(10)

(11)

证毕.

结 语

本研究探讨了频率测度论在保密通信中的应用问题，利用频率不相关性提出了不相关单钥密码系统的新概念，并利用不同于现有S盒的方式实现了加密变换的非线性．特别是在现有密码系统非线性性研究中普遍缺乏科学描述和严格理论证明的情况下，本文给出了一般单钥密码系统具有非线性性质的规范数学概念，并从理论上严格证明了将不相关基本单钥密码系统用于所有可能的保密通信中时，在一定条件下，保密通信系统几乎必然也具有不相关性．该结论说明了利用密文序列的任何线性运算难以对明文序列作出有把握的估计或推断，因而仅从利用密文单元对明文单元进行线性估计的角度来看，该保密通信系统具有较为理想的安全性．同时，该结论也说明了将不相关基本单钥密码系统用于实际保密通信时，存在某种应用场合或条件，使得整个保密通信系统具有不相关性．

另外，在对理论安全的保密通信系统进行实际模拟时，由于实际应用中的密钥单元序列通常只能是周期性的，尤其是常见分组密码算法和序列密码算法的密钥序列的现有实际使用方式都是周期性的，因此，本研究所得结果在模拟常见理论安全的保密通信系统中将会起一定的基础作用．频率测度论的其他知识在保密通信理论安全性及其密码算法设计中的应用将是今后的重要研究课题．

/ References：

[1] Shannon C E．Communication theory of secrecy system[J]．Bell System Technical Journal，1949，28(4)：656-715．

[2] Zhang Zhaozhi．Basis of modern cryptography[M]．Beijing：Beijing University of Posts and Telecommunications Publishing House，2004．(in Chinese) 章照止．现代密码学基础[M]．北京：北京邮电大学出版社，2004．

[3] Ren Wei．Modern cryptography[M]．Beijing：Beijing University of Posts and Telecommunications Publishing House，2011．(in Chinese) 任 伟．现代密码学[M]．北京：北京邮电大学出版社，2011．

[4] Konheim A G．Computer security and cryptography[M]．Tang Ming，Wang Houzhen，Han Haiqing，et al，trans．Beijing：Publishing House of Electronics Industry，2010．(in Chinese) Konheim A G．计算机安全与密码学[M]．唐 明，王后珍，韩海清，等，译．北京：电子工业出版社，2010．

[5] Li Shundong，Wang Daoshun．Modern cryptography：theory，method and research front[M]．Beijing：Science Press，2009．(in Chinese) 李顺东，王道顺．现代密码学：理论、方法与研究前沿[M]．北京：科学出版社，2009．

[6] Liu Jia．Security analysis of S-boxes in symmetric ciphers[J]．Journal of Nanjing University of Information Science and Technology: Natural Science Edition，2013，5(4)：352-357．(in Chinese) 刘 佳．对称密码算法S盒安全性分析[J]．南京信息工程大学学报：自然科学版，2013，5(4)：352-357．

[7] Ding Wenxia，Wang Hao．Design of S-boxes based on discrete chaos system[J]. Journal of National University of Defense Technology，2013，35(1)：83-88．(in Chinese) 丁文霞，王 浩．一种基于离散混沌系统的S-Box候选算法设计[J]．国防科技大学学报，2013，35(1)：83-88．

[8] Wang Y，Yang L，Li M，et al．A method for designing S-box based on chaotic neural network[C]// The 6th International Conference on Natural Computation．Yantai(China)：IEEE Press，2010：1033-1037．

[9] Wang Danhui, Wang An．The efficiency of power analysis attack based on S-boxes of block ciphers[J]．Journal of Shandong University Engineering Science, 2014，44(2)：6-11． 王丹辉，王 安．针对分组密码S盒的能量分析攻击效率研究[J]．山东大学学报工学版，2014，44(2)：6-11．

[10] Tian Chuanjun．Frequency measure theory[M]．Beijing：Science Press，2010．(in Chinese) 田传俊．频率测度论[M]．北京：科学出版社，2010．

[11] Deni H E Du． One over one million persons will only be able to play mathematical games[M]．Kao Yonggui，Nie Yongge，trans．Beijing：Publishing House of Electronics Industry，2010．(in Chinese) 亨利·E 杜德尼．1/1 000 000的人才会做的数学游戏[M]．考永贵，聂永革，译．北京：电子工业出版社，2010．

[12] Wu Heling．Magic square and prime number[M]．Beijing：Science Press，2008．(in Chinese) 吴鹤龄．幻方与素数[M]．北京：科学出版社，2008．

[13] Li Guanlin，Gu Daquan．Research on magic square method for programmer[J]．Microcomputer Applications, 2010，26(1): 17-18．(in Chinese) 李冠林，顾大权．幻方的实现方法研究[J]．微型电脑应用，2010，26(1)：17-18．

【中文责编：英 子；英文责编：雨 辰】

Frequency irrelevance and its applications in one-key cryptosystems

Tian Chuanjun†

College of Information Engineering, Shenzhen University, Shenzhen 518060, P.R.China

This paper explores applications of frequency measure theory in secrecy communication systems and studies the nonlinearity of encryption transformation in one-key cryptosystems. Aiming at the lack of normative description and strict demonstration in the theory for the nonlinearity of familiar block cipher systems, we introduce a strict mathematical definition and its implementation on nonlinear encryption transformation in general one-key cryptosystems. Based on the notion of irrelevance in the frequency measure theory, we propose a new definition called “irrelevant one-key cryptosystem” and testify to the existence of irrelevant basic one-key cryptosystems. In addition, we prove the following strong law of large numbers theoretically: sequences of message units and their corresponding cryptograph units are certainly irrelevant in probability 1 for any periodic sequence of secret keys on condition that the sequence of message units has a discrete memoryless uniform distribution during the secrecy communication process when an irrelevant basic one-key cryptosystem is used to transmit all possible messages secretly.

data security; secrecy communication system; irrelevant one-key cryptosystem; strong law of large numbers; frequency measure theory; irrelevance

：Tian Chuanjun．Frequency irrelevance and its applications in one-key cryptosystems[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(1): 32-39.(in Chinese)

TN 918

A

10.3724/SP.J.1249.2015.01032

国家自然科学基金资助项目(61070252)

田传俊(1964—)，男(汉族)，湖北省荆州市人，深圳大学教授．E-mail：tiancj@szu.edu.cn

Received：2014-01-15；Revised：2014-11-24；Accepted：2014-12-05

Foundation：National Natural Science Foundation of China(61070252)

† Corresponding author：Professor Tian Chuanjun．E-mail：tiancj@szu.edu.cn

引 文：田传俊．频率不相关性及其在单钥密码系统中的应用[J]. 深圳大学学报理工版，2015，32(1)：32-39.