全反射地震P 波的Goos－Hanchen 效应定量分析

袁龙刚，法 林

(西安邮电大学 电子工程学院，陕西 西安 710061)

光波在两种介质界面上反射时，反射点相对于入射点在相位上有一突变，而反射光相对于入射光在空间上有一段距离，这一距离被称为Goos－Hanchen 位移［1］。由于GH 位移深刻的物理内涵，自发现以来便受到物理学界的广泛关注，随后大量的实验证明，斜入射波的横向偏移现象是波所具有的共同特性之一。然而在地震勘探的理论研究与数据处理中，目前均未考虑波的横向偏移问题，实际上只要存在全反射就必然存在波的横向偏移，因此研究波的Goos－Hanchen 效应对地学参数的测量及地震勘探会有较大的影响，在测井分析与解释中也将具有应用前景。

1 P波在反射界面的反射系数

如图1 所示，当P 波入射到两介质界面上时，其反射系数为［2］

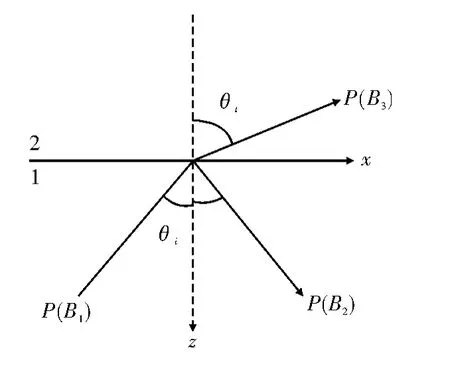
图1 P 波的反射

其中，B1，B2分别为波P 的入射波、反射波;ρ1c1和ρ2c2分别为介质1 和介质2 的特性阻抗。θi和θt分别为P波入射角和折射角，由斯奈尔定律得

若取θt=90°，则，此时若θi＞θic，θt将变成复角，则有［2］其中，j 为虚数单位。此时有RS=令则RS为

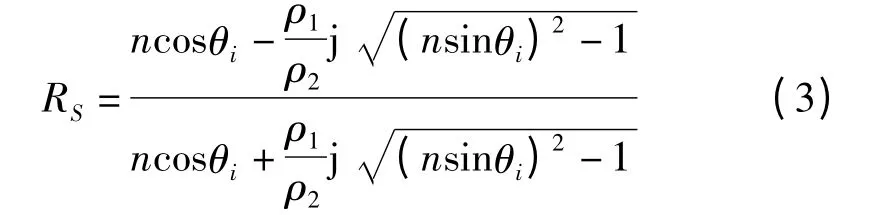
经计算可知δs为负值，且随着θi从θic增大到π/2的过程中逐渐由0 减小到－π。

2 P波在反射界面的横向偏移

在实际问题中，入射波总具有有限截面。此时，根据傅里叶分析的基本概念，入射波可看作许多平面波成分的叠加，这些平面波的传播方向以入射波的轴线方向为中心，而在其两侧呈连续变化，即不同平面波成分具有不同的入射角，当入射角θi变化时，相角δS亦随之发生变化，这即为产生Goos－Hanchen 位移的基础［4］。

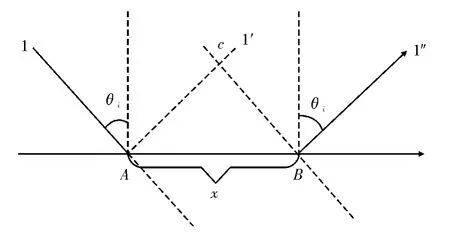
图2 GH 位移形成的原理

如图2 所示，A 为入射点;1 为入射波，1'为反射波。A 点的反射波相对于该点的入射波产生了相移δs，不难看出，由于入射波中各平面波成份的入射角不同，在A 点反射时相移δs也不同。故A 点反射波中各平面波成份的相对相位关系与入射波中各平面波成份的相对相位关系相比已发生了变化，其合成波形亦发生了变化。即A 点的反射不能形成像入射波那样能量定向集中的波束［4］。

由上式可知，介质界面对声波的反射产生了相角δs，为了补偿δs对反射波相位的影响，可考察界面上另一点B 反射波的相位。如图2 所示，B 点在A 点右方距离x 处，由虚线所示反射波面，可知B 点相位比A 点有一个落后差量δ'

式中，λ1为入射波在介质1 中的波长;ω 为入射波的中心频率;c1为入射波在介质中1 的传播速度，显然，对于给定的x，δ'随θi的增大而增大。即δ'对θi的依赖关系与δs相反。这样，便有可能找到某一适当的x，在相应位置B，反射波相对于A 点入射波的总相移量δS+δ'与θi无关，即

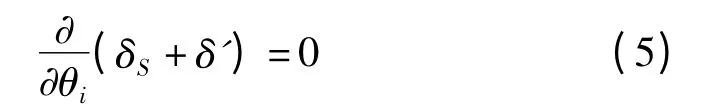
从而B 点出射的反射波中各平面波成份的相对相位关系仍保持在A 点入射的各平面波成份的相对相位关系不变，故B 点的反射波形与A 点入射波形一致，满足上式特定x 值即Goos－Hanchen 位移［5］

即

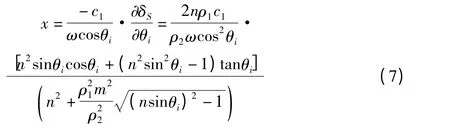
3 P波在反射界面的渡越时间

为了求出P 波在反射界面的渡越时间［6］，首先将cosθi和sinθi用kx和ω 表示并对其求导。

因介质界面对声波的反射产生了x 方向的横向偏移，波传播x 距离所需要的时间则为

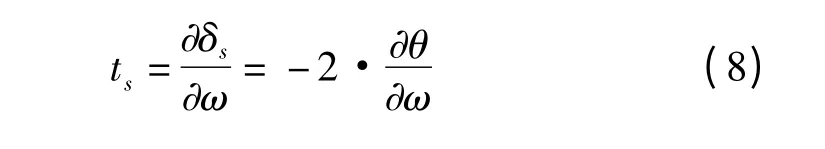
4 Goos－Hanchen 效应影响

为研究Goos－Hanchen 效应对地震P 波传播走势所造成的影响。文中选择了反射界面两侧介质参数差别较大的砂岩与致密砂岩。砂岩的纵波声速c1=4 740 m/s，ρ1=2.35 g/cm3，致密砂岩的纵波声速取c2=6 150 m/s，ρ2=2.66 g/cm3，波源频率ω=50 Hz，h=800 m，经计算可得到反射波的横向偏移曲线如下。

图3 反射波的横向偏移曲线

根据以上数据可求出入射波的入射临界角在51°附近。从图中可以看到，当入射角在52°附近和当入射角＞80°时，横向偏移随入射角的变化有较大的影响，而其他入射角的横向偏移与波长(λ≈600 m)在同一个数量级。

如图4 所示，当地震波从O 发射经界面M 点反射后再被S 接收的时距曲线方程为

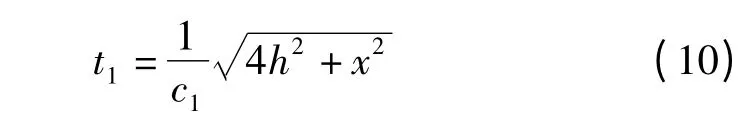
考虑横向偏移效应后，则由波源发射的波沿OC－D－S 的时距曲线方程为

其中，β 为实际入射角，显然t2更符合地震波传播的实际。若将上述所求的t1和t2相减，则有

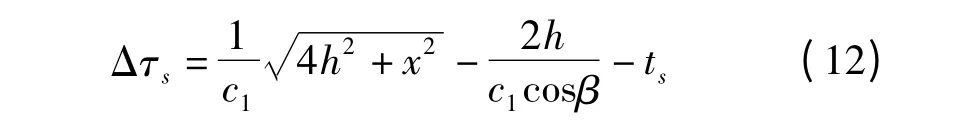
图4 振荡器比较电路

式(12)为计和不计横向偏移效应对地震波测量所产生的Goos－Hanchen 效应时差动校正量，计算结果如图5 所示。

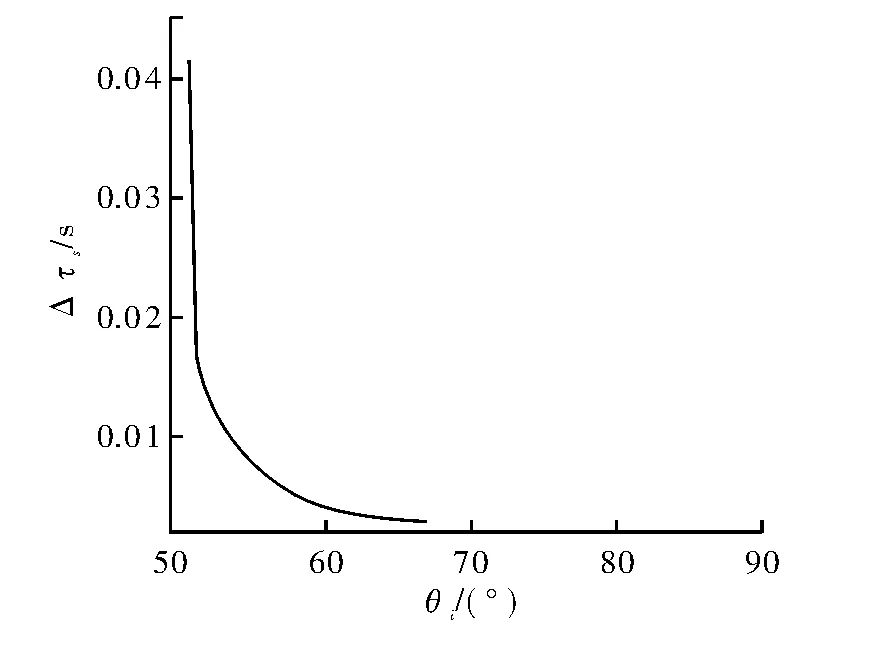
图5 两种传播路径下所产生的时差

在此应该注意，在考虑Goos－Hanchen 效应的相关计算时应采用约束条件［6］

约束条件方程是关于入射角β 的非线性方程，可通过数值方法求解。

如图6 所示［7］，在石油勘探测井中，T 是声波发射换能器;R 是声波接收换能器;L 是声系的源距;D 是套管的内径;θ0是声波从泥浆到套管的入射临界角。当P0波以入射临界角入射到套管时，在套管表面产生一段滑行波然后再反射到接收换能器。这一过程的时距曲线方程为

图6 声波测井示意图

其中，c1和c2分别为声波在泥浆和套管传播的纵波声速。考虑横向偏移效应后，则由发射换能器发射的波，沿T－C－D－R 传播到接收点的时距方程为

其中，θi是实际的入射角，且θi＞θ0;t2是考虑横向偏移效应后的结果，比t1更符合地震传播的实际，应有更高的准确度。则当D=200 mm，c1=1 500 m/s，c2=5 900 m/s，ρ1=1.2 g/cm3，ρ2=7.7 g/cm3，ω=20 kHz，L=1.4 m 时，计算得θ0=14.728 4°，t1=366.24 μs;当θi≈θ0时，t2=366.97 μs。

由以上数据可以看到，t1和t2尽管较为接近，但差异性仍存在。实际上在测井过程中接收换能器接收到叠加后的首波成份较复杂［8－10］，P0波在整个过程中只起到一部分贡献，所以这样看似微小的差异经多次叠加放大后所产生的误差也是不可忽视的。

5 结束语

本文利用反射波相角推导出了反射P 波在反射界面的横向偏移和横向偏移渡越时间，讨论了Goos－Hanchen 效应对P 波正常时差所造成的影响。该研究可用于地震波横向偏移效应的误差分析和校正。另外，在声波测井中考虑的主要是滑行波，但实际上只需存在全反射波，就必然存在Goos－Hanchen 效应，所以这个研究在测井分析与解释中也将具有应用前景。目前在地震数据处理及声波测井中还均未考虑Goos－Hanchen 效应的影响，现有的处理软件尚不具备Goos－Hanchen 效应校正功能。分析了P 波的Goos－Hanchen 效应，但还尚未涉及转换波的问题，不能用于分析存在转换波时Goos－Hanchen 效应的校正与计算，这是今后需进一步解决的问题。

［1］ Lotsh H K V.Beam displacement at total reflection:The Goos－Hanchen effect［J］.CA USA:Optik，1970.

［2］ 马大猷，沈豪.声学手册［M］.北京:科学出版社，1983.

［3］ 法林，J P Castagna，董和风.一种计算反射/传输系数的快速精确算法［J］.中国科学:G 辑，2008，38(7):873－895.

［4］ 蔡履中.Goos－Hanchen 位移的直观解释与简单推导［J］.大学物理，1994(4):6－8.

［5］ Castacna Jahn P，Brown Ray L.Effects of anisotropy on time－depth relation in transversely isotropic medium with a vertical axis of symmetry［J］.Chinese Science BulletinJuly，2010，55(21):2243－2251.

［6］ Liu F P，Wang A L，Li R Z，et al.The influence on normal moveout of total reflected SH－wave by Goos－Hanchen effect at an interface of strata［J］.Chinese Journal of Geophys，2009，52(8):2128－2134.

［7］ 法林，丛常喜，马玉英.声波水泥胶结测井的定量分析［J］.地球物理测井，1991，15(5):341－347.

［8］ Fa L，Xie W，Tian Y，Zhao M，et al.Effects of electric－acoustic and acoustic－electric conversions of transducers on acoustic－logging signal［J］.Chinese Science Bulletin，2012，57(12):1246－1260.

［9］ Wang Z.Seismic anisotropy in sedimentary rocks，part 2:laboratory data［J］.Geophysics，2002，67(3):1423－1440.

［10］Wang Z，Seismic anisotropy in sedimentary rocks，part 1:laboratory data［J］.Geophysics，2002，67(2):1414－1422.